1 引言
其中, 感知矩阵
重建稀疏信号是CS理论的首要目标. 因为
众所周知, 寻找最优的解需要穷尽一切可能的搜索, 这是NP -难的. 因此, 需要寻找一种有效率的重建算法取代穷尽的搜索. 此时, 正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法由于它易操作和高效率而引起关注. OMP算法[6]是一种迭代型贪婪算法. 其原理为: 在每次迭代中, 选择与当前残差内积绝对值最大的矩阵的一个列来逐步逼近原始信号. 许多学者研究OMP算法的改进形式. 比如分段正交匹配追踪(Stagewise OMP, StOMP)[7]算法, 压缩采样匹配追踪(Compressive Sampling MP, CoSamp)[8]算法, 子空间追踪(Suspace Pursuit, SP) [9]算法, 广义正交匹配追踪(generalised OMP, gOMP)[10]算法等. 本文提出OMP算法的一种改进方法来重建稀疏信号. 相比于标准的OMP算法, 唯一的区别是加入系数阈值判断机制.
测量矩阵
定义1.1[11] 测量矩阵
定义1.2[12] 测量矩阵
对任意
考虑到一些矩阵满足限制等距性, 但不满足相干性条件的情况, 许多学者研究了重建算法下采样矩阵的限制等距性. 在无噪声情况下(即,
本文的主要内容如下.
首先, 基于这篇文章的框架有以下假设与引理
(A1)
(A2)
(A3)
(A4)
(A5)
引理1.1[12] 对于
引理1.2[12] 令
引理1.3[12] 令
定义1.3 信号
定义1.4 信号
2 主要结果
OMP算法步骤如下
在搜寻过程中, 如果有一个原子选错了, OMP算法的输出将不正确. 为了改进OMP算法的重建性能, 引入一个阈值判断机制.
为了确保每次迭代中选择一个正确的原子, 我们分析第
噪声下, OMP算法求解的最优化问题为
引理2.1 假设
在文献[21]的引理
定理2.1 假设感知矩阵
证 证明包括两个步骤. 首先分别给出OMP算法在第
由算法的步骤
为了证明式(2.2), 等价于证明
由算法的步骤
第一次迭代选择正确的原子.
在第一次迭代, OMP算法选中的一个原子
另一方面, 如果在第一次迭代, OMP算法选错了一个原子
由式(2.4)和式(2.5), 为证式(2.3), 需证
由引理2.1, 得
接下来给出不等式(2.6)右边的上界. 明显地, 存在
(a):
因此, 式(2.6)可由下式保证
进一步地
可证式(2.7)成立如果
成立, 即
成立.
第
假设OMP算法在前面
和
由式(2.9)和式(2.10), 要证式(2.3), 只需证
接下来, 给出式(2.11)左边的一个下界. 由假设
接下来, 给出式(2.11)右边的一个上界. 由假设
(b):
联立式(2.12)和式(2.13), 式(2.11)可由下式保证
即
进一步地, 观察到
要证式(2.11)也可由下式保证
定理2.1证毕.
注2.1 由式(2.13), 在
(a): 由引理1.3可得. 由
引理2.2 如果矩阵
证 要证的式子可以转化成
这时
对任意正整数
得到
定理2.2 假设
使得OMP算法在
在
证 要证存在线性模型
接着得到
由式(2.15), 有
可见该模型满足定理2.2的条件, 然而, OMP算法未能精确恢复信号
OMP算法不能保证在第一次迭代中选择正确的原子.
3 数值模拟
3.1 不同SNR程度下的信号恢复
很难设计出采样矩阵的任意阶都满足定理2.1中RIC的界. 该实验借助文献[13]的矩阵, 其RIC常数小于0.2.
令
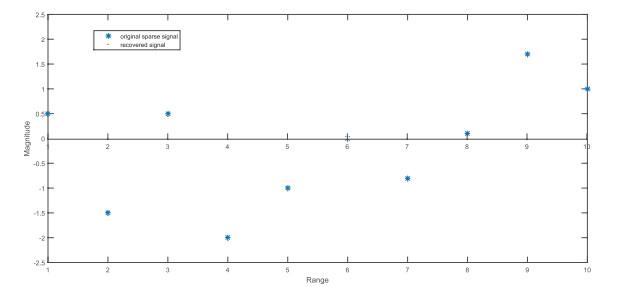
图 1
从图 1中看出, 重建信号不能识别原始信号
保持9 -稀疏信号
表 3证明定理2.1的结论: 如果SNR值满足定理2.1的充分条件, 并且矩阵满足RIC条件, 支撑可以被准确的识别.
表 1 OMP算法
| 输入: 样本 |
| 步骤1(识别): |
| 步骤2(增加): |
| 步骤3(估计): |
| 步骤4(更新): |
| 输出: 重建信号 |
表 2 改进的OMP算法
| 输入: 样本 |
| 步骤1(识别): |
| 步骤2(增加): |
| 步骤3(估计): |
| 步骤4(筛选): 若 |
| 是, 接着步骤5, 否则, 步骤1. |
| 步骤5(更新): |
| 输出: 输出信号 |
3.2 不同噪声水平的信号恢复
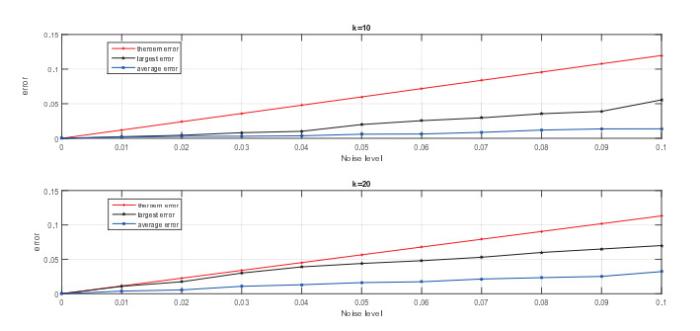
根据前面的分析, 即使原始信号的支撑被准确识别, 原始稀疏信号由于存在的噪声仍然不能精确的重建. 该实验的噪声范围在0到0.1并每隔0.01取一次, 接着, 对于每个噪声水平, 采取一个新的测量矩阵服从随机独立分布, 测量信号由
图 2
图 3
图 2证明了理论上界的误差范围: 当稀疏度
3.3 改进算法下的图像去噪
当噪声是Gaussian噪声时. 原始清晰图像是
在本次实验中, 模糊的图像在改进OMP算法的重建下图像较清晰.
参考文献
Compressed sensing
DOI:10.1109/TIT.2006.871582 [本文引用: 1]
Single-pixel imaging via compressive sampling
DOI:10.1109/MSP.2007.914730 [本文引用: 1]
The power of convex relaxation: Near-optimal matrix completion
Improved pediatric MR imaging with compressed sensing
DOI:10.1148/radiol.10091218 [本文引用: 1]
Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information
DOI:10.1109/TIT.2005.862083 [本文引用: 1]
Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit
DOI:10.1109/TIT.2011.2173241 [本文引用: 1]
Iterative signal recovery from incomplete and inaccurate samples
DOI:10.1016/j.acha.2008.07.002 [本文引用: 1]
Subspace pursuit for compressive sensing signal reconstruction
Generalized orthogonal matching pursuit
DOI:10.1109/TSP.2012.2218810 [本文引用: 1]
Analysis of orthogonal matching pursuit using restricted isometry property
DOI:10.1109/TIT.2010.2054653 [本文引用: 2]
The orthogonal super greedy algorithm and applications in compressed sensing
DOI:10.1109/TIT.2011.2177632 [本文引用: 1]
Near optimal bound of orthogonal matching pursuit using restricted isometric constant
On the recovery limit of sparse signals using orthogonal matching pursuit
DOI:10.1109/TSP.2012.2203124 [本文引用: 1]
Near optimal condition of OMP algorithm in recovering sparse siganl from noisy measuurement
DOI:10.1109/JSEE.2014.00063 [本文引用: 1]
Improved RIP analysis of orthogonal matching pursuit
An improved RIP-based performance guarantee for the sparse signal recovery via orthogonal matching pursuit
A sharp restricted isometry constant bound of orthogonal matching pursuit
A sharp condition for exact support recovery with orthogonal matching pursuit
DOI:10.1109/TSP.2016.2634550 [本文引用: 3]