1 引言
分数阶广义系统是分数阶系统和广义系统的有机结合, 它是微分约束部分用分数阶导数刻画的微分代数系统. 它适于描述状态变量间既存在分数阶微分约束, 又存在代数约束的复杂系统[12]. 目前学术界对于分数阶广义系统的研究集中于: 1) 研究分数阶广义系统的稳定性、容许性、系统镇定[12-16]等问题. 文献[12]是研究分数阶广义系统的奠基性工作. 该文在无脉冲的前提下, 分别针对导数阶数
系统观测器设计是控制理论应用于工程实践的重要方面. 现有分数阶广义线性系统观测器设计方法比较繁琐, 不便于工程应用. 文献[21]是关于分数阶广义线性系统及其状态观测器设计方面的奠基性工作. 文中提出的观测器设计方法, 需要确定
如果转变思路, 将系统状态观测器及其误差系统设计为分数阶广义线性系统的形式, 就可以减少参数矩阵的引入, 从而得到更加便捷实用的观测器设计方法. 这一思路面临的挑战是, 具有分数阶广义线性系统形式的状态观测器很可能含有脉冲, 这就需要对含脉冲的分数阶广义线性系统的状态响应和稳定性等理论进行研究.
本文首先研究了含有脉冲项的分数阶广义线性系统的分布解, 阐述系统分布解如何表征分数阶系统的"记忆特性". 以系统分布解为基础, 本文证明了含有脉冲项的分数阶广义线性系统的渐近稳定性定理, 据此给出了具有分数阶广义线性系统形式的状态观测器设计依据和方法. 该观测器设计方法仅涉及一个待定列向量, 且只需确定其中部分元素, 设计方法简单便捷. 最后, 仿真实例验证了观测器对系统状态的重构准确有效.
2 分数阶广义线性系统的分布解
脉冲函数
2.1 脉冲函数的Caputo导数及其Laplace变换
脉冲函数
定义2.1
本文用到的
命题2.1 设函数
命题2.2
命题2.3
Caputo导数是应用中常见的分数阶导数, 其完整定义如下[1].
定义2.2
Caputo导数的Laplace变换仅涉及函数整数阶导数的初值, 较为常用, 其形式如下.
命题2.4
此外, 以下性质给出了函数
命题2.5 当
将上述Caputo导数定义, 运用到函数
定义2.3
利用上述命题以及定义, 我们可以得到
定理2.1
证
(1) 若
(2) 若
定理2.1证毕.
定理2.2和推论2.1给出了
定理2.2
证 根据定义2.3中
(1) 当
由于
(2) 当
(3) 当
显然,
定理2.2证毕.
定理2.2将命题2.3中
推论2.1
2.2 分数阶广义线性系统的分布解
其中
2.2.1 分数阶广义线性系统慢子系统的解
显然, 慢子系统(2.2.1)是分数阶线性系统, 其状态响应可由如下定理2.3[17]给出.
定理2.3 系统(2.2.1)的解形式如下
其中
2.2.2 分数阶广义线性系统快子系统的分布解
快子系统的状态响应是含有脉冲项的分布解, 我们证明如下定理2.4.
定理2.4 快子系统(2.2.2)的状态响应如下
证 对快子系统(2.2.2)两边同时施行Laplace变换, 则有
移项整理之,
将
利用推论2.1, 对(2.7)式两边同时进行Laplace逆变换, 可得
计算
移项之
于是
从而有
将(2.9)式带入(2.8)式, 得到快子系统(2.2.2)的状态响应
其中
定理2.4证毕.
分数阶广义线性系统的分布解显著刻画了分数阶广义线性系统的"记忆特性". 快子系统的状态响应(2.4)包含脉冲项和控制输入
综上所述, 分数阶广义线性系统的分布解(2.4)显著刻画了系统对其快子系统的初值、控制输入及其各阶导数的"记忆特性", 分布解包含的脉冲项更明显地反映了系统的记忆效应.
3 分数阶广义线性系统的稳定性
研究分数阶广义线性系统的渐近稳定性是设计系统观测器的前提. 目前关于分数阶广义线性系统渐近稳定性的研究, 是建立在系统无脉冲的基础上的. 利用定理2.1和定理2.4, 可以证明含脉冲的分数阶广义线性系统的渐近稳定性定理.
3.1 分数阶广义线性系统稳定性的概念
定义3.1 对于正则分数阶广义线性系统(3.1)
若由任意初始状态
3.2 分数阶广义线性系统稳定性定理
文献[21]指出分数阶线性系统是渐近稳定的充要条件是: 系统矩阵
定理3.1 正则分数阶广义线性定常系统(3.1)是渐近稳定的充要条件是矩阵对
证 先对正则分数阶广义线性定常系统(3.1)的状态方程进行受限等价变换, 其慢子系统(3.1.1)和快子系统(3.1.2)分别为
显然, 慢子系统是分数阶线性定常系统, 该部分渐近稳定的充要条件是矩阵
由定理2.1, 脉冲项
从而有
显然, 快子系统(3.1.2)是渐近稳定的. 综合慢子系统和快子系统的渐近稳定性, 知系统(3.1)是渐近稳定的充要条件是其慢子系统(3.1.1)矩阵
下面证明, 在受限等价变换下, 原系统(3.1)和慢子系统(3.1.1)的特征值集合相等, 即
经受限等价变换后, 系统的特征值不变, 其特征多项式可表为
考虑到
可见, 受限等价变换后的系统和其慢子系统具有相同特征值, 因此
综上所述, 系统(3.1)是渐近稳定的充要条件是其矩阵对
定理3.1说明, 脉冲项不影响分数阶广义线性系统的稳定性. 因此含脉冲的分数阶广义线性系统的稳定性和分数阶线性系统、无脉冲分数阶广义线性系统的稳定性条件相同.
4 分数阶广义线性系统的观测器设计
基于定理3.1, 本节主要研究具有分数阶广义线性系统形式的状态观测器的存在条件和设计方法.首先给出分数阶广义线性定常系统的状态观测器的概念.
针对分数阶广义线性系统(2.1), 如果存在一个以系统(2.1)的输入
定义4.1 形如式(4.1)的动态系统观测器(
称为系统(2.1)的全维闭环状态观测器, 其中
4.1 分数阶广义线性系统观测器的存在性
结合含脉冲分数阶广义线性系统的渐近稳定性定理3.1, 可以证明分数阶广义系统(2.1)存在全维闭环状态观测器(4.1)的充要条件, 即定理4.1.
定理4.1 正则分数阶广义线性系统(2.1)存在全维状态观测器(4.1)的充要条件是存在矩阵
证 将两个状态方程(2.1.1)和(4.1.1)相减, 可得
作误差变量,
由定理3.1, 系统(4.2)渐近稳定, 即
4.2 分数阶广义线性定常系统观测器的设计
由定理3.1的证明过程可知, 具有分数阶广义线性系统形式的状态观测器, 其快子系统的状态响应中会出现脉冲项. 但脉冲项将随着时间的增长, 衰减为0, 它不影响系统稳定性, 它对观测器跟踪效果的影响也将衰减为0. 从而慢子系统的稳定性决定了系统(3.1)的稳定性. 因此, 更好的思路是仅针对系统(3.1)的慢子系统设计观测器. 我们可以通过适当指定增益矩阵
定理4.2 若正则分数阶广义线性系统(2.1)经过受限等价变换后, 其慢子系统是完全能观的, 则原系统(2.1)具有形如(4.1)式的全维状态观测器.
证 对被观测系统(2.1)左乘可逆矩阵
对观测器(4.1)左乘可逆矩阵
其中
令
从而观测器状态方程(4.4)可以表为
用(4.3)式的状态方程减去(4.6)式有
(4.7)式上下两部分的结构特点, 便于我们得到其特征多项式
由于原系统的慢子系统是完全能观的, 其对偶系统完全能控, 可进行任意极点配置. 即存在
对(4.5)式的第一式两边同乘
4.3 分数阶广义线性系统观测器的设计方法
综上所述, 具有分数阶广义线性系统形式的全维状态观测器(4.1)设计算法如下.
Step 1 针对所给系统进行受限等价变换, 得到标准型;
Step 2 提取慢子系统的系数矩阵
Step 3 对
Step 4 计算原系统的增益矩阵
Step 5. 得到原系统的全维状态观测器(4.1).
5 实例仿真
例1 针对以下正则分数阶广义线性定常系统设计状态观测器
解 取非奇异变换矩阵
进行受限等价变换后, 系统(5.1)被等价地变换为如下标准型(5.2)
(5.2.1)式是(5.2)式的慢子系统部分, (5.2.2)式是其快子系统部分, 显然有
考虑该慢子系统的能观性, 能观性矩阵
系统稳定性要求任意期望极点
设系统增益矩阵
其特征多项式为
由期望极点构成的特征多项式为
于是我们得到系统(5.1)的慢子系统状态观测器方程为
下求观测器的增益矩阵
因此, 原系统的状态观测器是
下面验证观测器(5.5)能正确观测原系统(5.1)的状态轨迹。由方程(4.3)和(4.6)可知, 在被观测系统与其状态观测器中, 控制输入
取系统(5.2)的初值为
快子系统(5.2.2)的响应为
从而系统(5.2)的状态响应为
系统观测器(5.5)经等价变换后, 任取其初值
其解为初值引起的响应
其中,
快子系统
解为
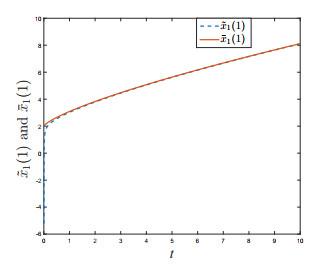
图 1–3给出了
图 1
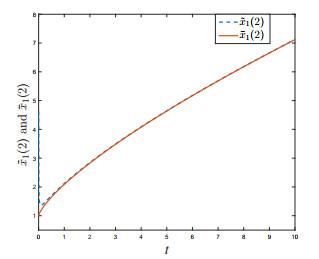
图 2
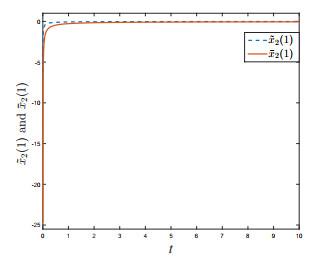
图 3
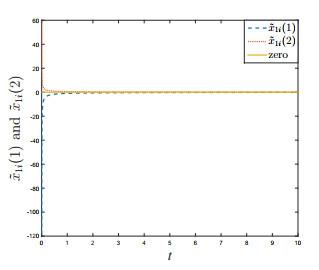
其中
图 4
6 结论
本文研究了分数阶广义线性系统的状态观测器设计问题. 我们首先研究了脉冲函数
参考文献
Analysis of fractional differential equations
Analysis of a system of fractional differential equations
DOI:10.1016/j.jmaa.2004.01.013
Theory of fractional functional differential equations
Fractiona calculus: A mathematical method of describing the memory characteristic and intermediate process
Applications of fractional calculus to the theory of viscoelasticity
DOI:10.1115/1.3167616 [本文引用: 1]
Fractional rheological models of dynamic mechanical behavior of magnetoactive elastomers in magnetic fields
Stability of a linear oscillator with damping force of fractional-order derivative
Robust stabilization of uncertain descriptor fractional-order systems
DOI:10.1016/j.automatica.2013.02.066
New admissibility conditions for singular linear continuous-time fractional-order systems
Sufficient and necessary condition of admissibility for fractional-order singular system
DOI:10.1016/S1874-1029(14)60003-3 [本文引用: 2]
Necessary and sufficient conditions of observer-based stabilization for a class of fractional-order descriptor systems
DOI:10.1016/j.sysconle.2017.12.004 [本文引用: 2]
Descriptor fractional linear systems with regular pencils
DOI:10.1002/asjc.579 [本文引用: 4]
On the existence and uniqueness of the solution of linear fractional differential-algebraic system
Singular fractional linear systems and electrical circuits
DOI:10.2478/v10006-011-0028-8 [本文引用: 1]
Reduced-order observer design with unknown input for fractional order descriptor nonlinear systems
DOI:10.1177/0142331219834990 [本文引用: 1]