1 引言
双曲守恒律方程是计算流体力学中一类重要的方程, 如海洋学中的浅水波方程、空气动力学中的Euler方程和交通流领域中的LWR模型等. 即使初始条件充分光滑, 该类方程的解也可能会在某个时刻出现间断. 解在间断附近有着丰富和复杂的结构, 这给数值解法的构造带来了诸多挑战. 为了研究间断解, Lax[1]提出了弱解的概念, 允许间断解的存在. 但弱解并不唯一, 如何在众多弱解中寻找具有物理意义的相关解呢? 随后, Lax[2]依据热力学第二定律提出了熵稳定条件, 满足该条件的数值格式产生的数值解能收敛于唯一且具有物理意义的解. 为了实现熵稳定, Tadmor[3]介绍了熵变量和熵势的概念, 设计了一类具有二阶精度的熵守恒格式, 并严格证明了一个三点格式只需含有比熵守恒格式更多的数值粘性则是熵稳定的. 基于此, 通过对熵守恒格式添加合适的耗散项就可以得到熵稳定格式. Lefloch等[4]提出了由二阶熵守恒格式构造任意偶数阶熵守恒格式的方法, 并将此高阶熵守恒通量与满足保号性的ENO重构数值耗散算子相结合, 得到TECNO格式. 为了构造高阶熵稳定格式, 熵变量在每个单元交界面上重构值的跳跃与原始值的跳跃需保持符号一致.
目前, 仅有一小类重构满足保号性. 程晓晗[5]通过对二次多项式进行恰当限制, 提出了一种三阶保号的重构. Fjordholm[6]提出的ENO插值和基于Minmod限制器的二阶TVD重构均满足保号性. 然而, TVD重构在解的极值处可能会降低精度, ENO重构由于不稳定模板的选择也可能会导致精度降低. 众所周知, WENO重构优于ENO重构. WENO重构是对各个候选模板进行非线性加权, 每个模板权值的选取依赖于该模板上数值解的局部光滑性, 进而克服了ENO重构的缺点. 在光滑区域, WENO格式比ENO格式精度更高、收敛性更好; 而在间断附近, 仍保留ENO格式的良好性质. 基于此, Fjordholm和Ray[7]提出了一种保号的三阶WENO重构方法(称为SP-WENO), 并用标量方程进行测试. 随后, Biswas和Dubey[8]基于TECNO框架, 构造了保号的TVD重构和三阶WENO重构耗散算子. 更多结果参见文献[9-22].
本文以熵稳定格式为基础, 以TECNO框架作为设计原则, 构造了一种高阶保号熵稳定格式. 从理论推导和数值实验两方面验证了三阶紧致CWENO重构熵变量满足保号特性.
2 预备知识
考虑如下守恒律方程
其中向量
这里
考虑
这里
其中数值通量
2.1 熵守恒通量
定理2.1[3] 若
那么格式
这里
注意到, 条件
但对于守恒律方程组
上述定义的熵守恒通量只有二阶精度, LeFloch等[4]通过对二阶精度熵守恒通量进行线性组合, 构造了
式中
特别地, 四阶熵守恒通量
这些熵守恒格式适用于熵保持的光滑问题, 但在激波处会出现伪振荡. 而这些伪振荡产生的原因是: 熵守恒格式无法在激波附近产生足够的熵增量. 故需为熵守恒通量添加适当的耗散算子, 以抑制伪振荡的产生.
2.2 熵稳定通量
熵稳定格式包含两个关键要素:
(i) 如何恰当地使用熵变量;
(ii) 是否比熵守恒格式含有更多的数值粘性.
定理2.2[23] 假设
那么, 格式
设
数值熵的耗散, 特别是间断附近的耗散, 若熵过多, 间断附近会出现抹平现象; 若熵不足, 间断附近会产生伪振荡. 为构造恰当的数值耗散, Ismail和Roe[9]对Euler方程的耗散算子做出如下修正
其中
这里
同理, 可以将耗散算子推广到浅水波方程组中,
2.3 高阶熵稳定通量
对
这里
根据定理2.2, 若标量熵变量
则通量
定义2.1 在每一个单元交界面
则该重构在
该文基于TECNO框架提出了一种鲁棒的、耗散较小的熵稳定格式, 该格式允许使用跨越跳跃间断的保号高阶重构, 且耗散项仅在保号处起作用. 即
其中
(i) 对于标量方程
(ii) 对于守恒律方程组:
其中
3 保号的紧致CWENO重构
三阶紧致CWENO重构是一个基于不同模板上插值多项式的凸组合. 该重构基于定义一个二次函数, 将该函数添加到线性插值中, 会在光滑区域达到三阶精度; 对于不连续或大梯度区域, 会自动切换到单侧线性重构. 对于标量方程, 该文用三阶紧致CWENO重构熵变量
其中
引理3.1 若不等式
成立, 则称离散集
定理3.1 三阶紧致CWENO重构
证 设
令
考虑三阶紧致CWENO重构:
那么熵变量在单元交界面
在条件
故由条件
4 数值算例
本节采用熵稳定格式
这里
4.1 线性对流方程
采用周期性边界条件, 在区间
表 1 CCWENO3格式在初始条件为(4.3)式时, CFL = 0.5, T = 1处的收敛率
| N | L1 error | Rate | L∞ error | Rate |
| 40 | 0.001979313043305 | 3.629516311932702e-04 | ||
| 80 | 2.726027476503843e-04 | 2.86 | 7.092855086397350e-05 | 2.36 |
| 160 | 3.522356279884232e-05 | 2.95 | 9.975669895746602e-06 | 2.83 |
| 320 | 4.405706993699641e-06 | 3.00 | 1.260137438287312e-06 | 2.99 |
| 640 | 5.373835462491922e-07 | 3.01 | 1.576597490888024e-07 | 3.00 |
图 1
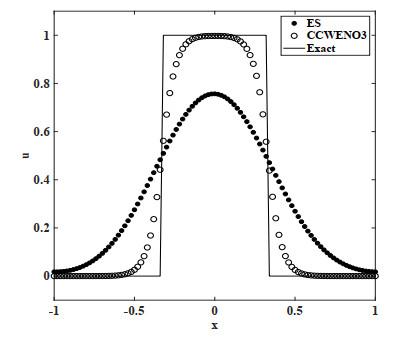
4.2 Burgers方程
采用周期性边界条件, 在区间
Burgers方程是一类非线性标量问题, 取熵函数
取EC1耗散矩阵
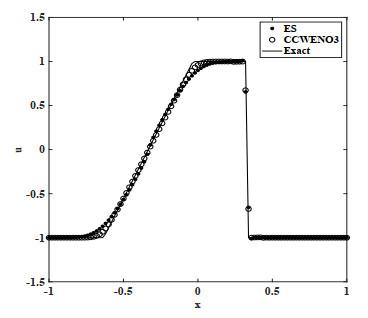
对于连续性初值问题
表 2 CCWENO3格式在初始条件为(4.6)式时, CFL = 0.5, T = 0.32处的收敛率
| N | L1 error | Rate | L∞ error | Rate |
| 40 | 1.827054747602715e-04 | 1.448773504797440e-04 | ||
| 80 | 2.851024314352313e-05 | 2.68 | 1.785661053588239e-05 | 3.02 |
| 160 | 3.845862448196772e-06 | 2.89 | 2.226299234296333e-06 | 3.00 |
| 320 | 4.929538860536765e-07 | 2.96 | 2.782109209450295e-07 | 3.00 |
| 640 | 6.139221843903657e-08 | 3.01 | 3.478015911254420e-08 | 3.00 |
图 2
图 3
4.3 Euler方程
理想气体的一维Euler方程为
其中
其中
取熵对
可得熵变量
Ismail和Roe[9]为Euler方程构造了
则单元交界面
其中
下面给出求解一维Euler方程
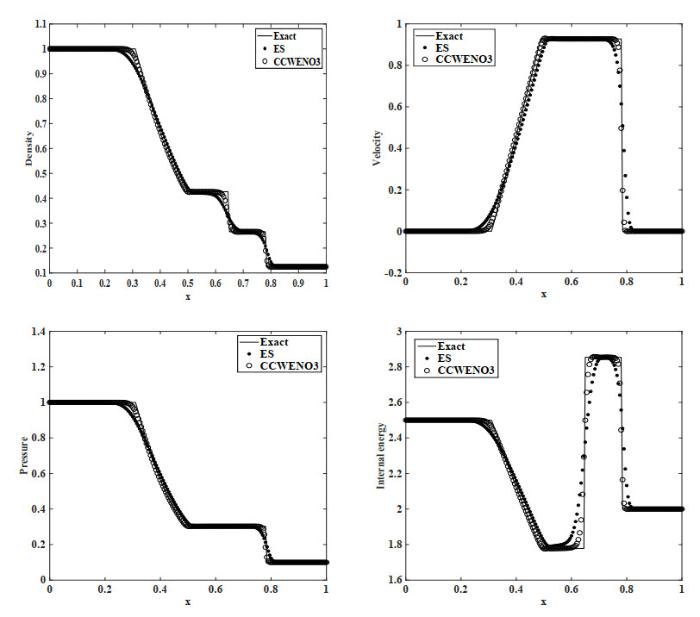
(1) Sod激波管问题,初始条件为
Sod激波管问题的初始间断包含左稀疏波, 接触间断和右激波. 本文计算了
图 4
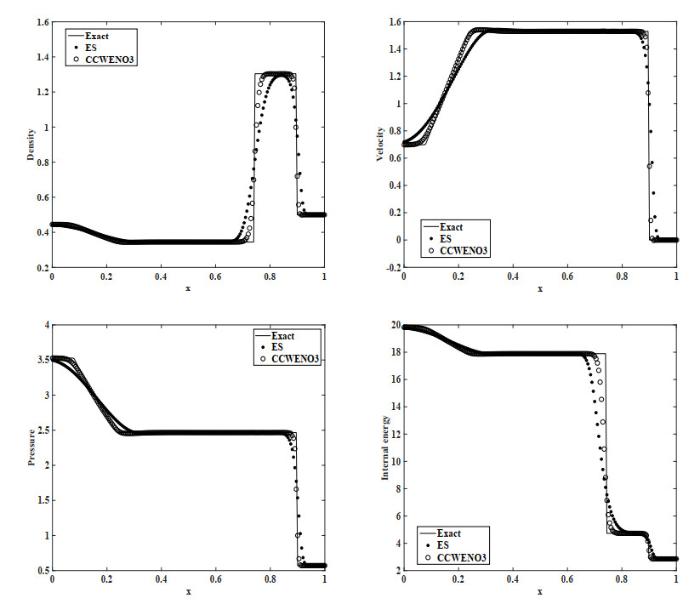
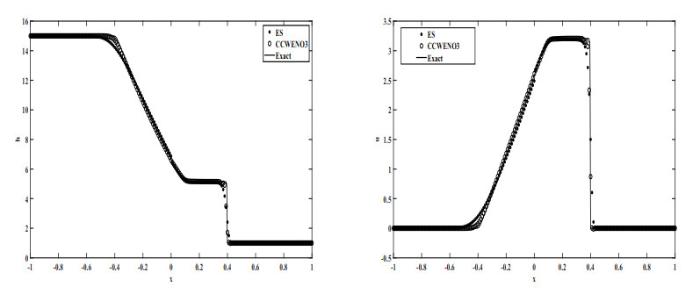
(2) Lax激波管问题,初始条件为
Lax激波管问题包含了真正的非线性场(稀疏波, 激波)和线性退化场(接触间断). 其计算区间均为
图 5
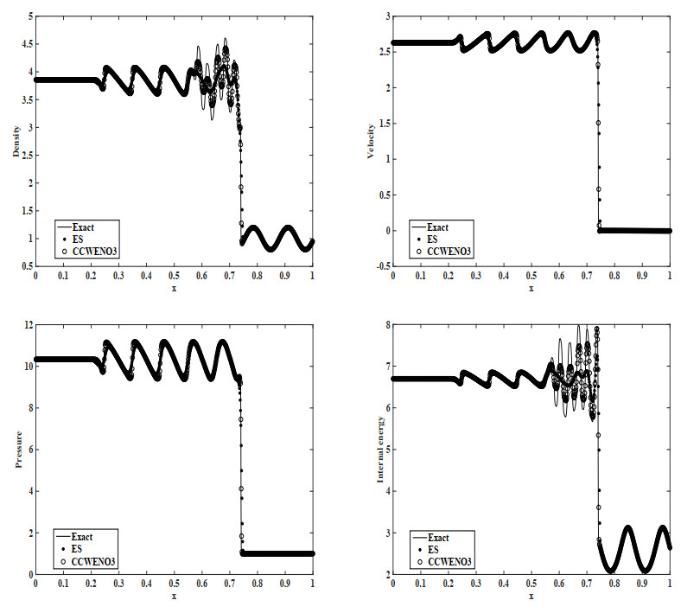
(3) Shu-Osher问题, 初始条件为
在该测试中, Mach 3激波与声波相互作用, 既有强的和弱的激波, 又有高度振荡但平滑的波. 该测试求解复杂, 可以很好地检测所构造格式的性能. 本文在具有自由流动边界的计算域
图 6
4.4 浅水波方程
其中
其中
相应地, 熵变量和熵势的表达式分别为
熵守恒通量
满足
耗散矩阵
(1) 溃坝问题, 初始条件为
溃坝问题的解由左行稀疏波和右行激波组成. 在区间
图 7
(2) 大型溃坝问题, 初始条件为
大型溃坝问题结果包含左行稀疏波和右行激波. 计算到
图 8
5 总结
本文给出了高阶熵稳定格式的构造过程. 高阶熵稳定格式的构造需要使用一种满足保号性质的方法来重构单元交界面上的熵变量. 只有少数几种方法满足这一性质, 该文提出了一种三阶保号的紧致CWENO型重构, 并基于修正的TECNO框架, 将高阶熵守恒通量与高阶数值耗散算子结合得到了高阶精度保号的熵稳定格式, 该格式具有如下特点:
(1) 对于双曲守恒律方程组的光滑解可以达到任意阶精度.
(2) 满足离散熵不等式, 是严格熵稳定的.
(3) 每个单元交界面上重构的跳跃与相应单元格值的跳跃具有相同的符号.
(4) 保留紧致CWENO格式的优点, 重构跳跃值具有对称性且计算经济, 即在相同精度要求下所用节点少.
(5) 精准捕捉解的结构, 有效避免非物理现象, 间断附近基本无振荡, 高分辨率, 且具有良好的鲁棒性等.
参考文献
Weak solutions of nonlinear hyperbolic equation and their numerical computation
DOI:10.1002/cpa.3160070112 [本文引用: 1]
Hyperbolic systems of conservation laws and the mathematical theory of shock waves
The numerical viscosity of entropy stable schemes for systems of conservation laws
DOI:10.1090/S0025-5718-1987-0890255-3 [本文引用: 2]
Fully discrete, entropy conservative schemes of arbitrary order
DOI:10.1137/S003614290240069X [本文引用: 2]
A third-order entropy stable scheme for hyperbolic conservation laws
DOI:10.1142/S021989161650003X [本文引用: 1]
Arbitrarily high-order accurate entropy stable essentially nonoscillatory schemes for systems of conservation laws
DOI:10.1137/110836961 [本文引用: 3]
A sign preserving WENO reconstruction method
Low dissipative entropy stable schemes using third order WENO and TVD reconstructions
DOI:10.1007/s10444-017-9576-2 [本文引用: 1]
Affordable, entropy-consistent Euler flux functions II: entropy production at shocks
DOI:10.1016/j.jcp.2009.04.021 [本文引用: 3]
Compact central WENO schemes for multidimensional conservation laws
DOI:10.1137/S1064827599359461 [本文引用: 1]
Analysis and design of numerical schemes for gas dynamics, 1:Artificial diffusion, upwind biasing, limiters and their effect on accuracy and multigrid convergence
Total variation diminishing Runge-Kutta schemes
DOI:10.1090/S0025-5718-98-00913-2
High-order accurate, fully discrete entropy stable schemes for scalar conservation laws
The construction of discretely conservative finite volume schemes that also globally conserve energy or entropy
On the total variation of a third-order semi-discrete central scheme for 1D conservation laws
Numerical entropy production for central schemes
Entropy stability theory for difference approximations of nonlinear conservation laws and related time-dependent problems
Energy preserving and energy stable schemes for the shallow water equations
非等熵Chaplygin气体测度值解存在性
DOI:10.3969/j.issn.1003-3998.2020.04.001
The existence of the measure solution for the non-isentropic chaplygin gas
DOI:10.3969/j.issn.1003-3998.2020.04.001
等熵Chaplygin气体的二维Riemann问题
DOI:10.3969/j.issn.1003-3998.2017.06.005
The two-dimensional riemann problem for isentropic chaplygin gas
DOI:10.3969/j.issn.1003-3998.2017.06.005
可压缩磁流体动力方程解的正则性
Regularity criteria for the compressible magneto-hydrodynamic equations
Perfect derivatives, conservative differences and entropy stable computation of hyperbolic conservation laws
DOI:10.3934/dcds.2016.36.4579 [本文引用: 2]