1 引言
与根据时间和空间直接离散控制方程的传统宏观数值方法不同, 格子Boltzmann方法(LBM)是一种介观的数值计算方法[8]. LB方程基于一个基本的离散速度动力学方程, 它包括粒子碰撞和迁移基本过程, 这两个过程可以清楚地还原出各种宏观物理现象. 为了将微观LB输运方程与宏观流体动力学方程联系起来, 文献[9]使用Chapmann-Enskog多尺度展开技术, 把Knudsen数
基于LBM的NLEEs的数值研究一般考虑常系数NLEEs, 在物理环境中, 当考虑到介质的不均匀性和边界的不均一性时, 变系数非线性偏微分方程比常系数偏微分方程更能反映实际情况. 文献[11], 着重于一个具有时变系数的广义Gardner方程, 方程(1.1)被用来模拟弱非线性长波在KdV型介质中的传播, 这种介质的特征是色散和非线性系数会发生变化, 可以描述大气阻塞现象.
其中,
文献[12]研究了一类变系数的复合Korteweg-de Vries-Burgers(vc-cKdVB)方程, 它是一种在固体材料、等离子体、流体等领域广泛使用的物理模型.
其中, 参数
本文的主要内容如下: 在第2节中, 利用Taylor展开和Chapmann-Enskog多尺度展开技术, 证明了带有修正项的格子Boltzmann模型与变系数KdV-Burgers宏观方程是相容的, 并由宏观方程的系数构造了平衡态分布函数和修正函数. 在第3节中, 利用MATLAB进行数值模拟, 给出不同时刻变系数方程的时空演化图和误差分析图, 并对模型的空间精度和时间精度进行数值分析. 第4节对本文研究的结果进行了总结和展望.
2 非线性系统的格子玻尔兹曼模型
带有修正项的离散分布函数的LB方程
其中,
对(2.1)式进行多元Taylor展开, 并保留到
利用Chapmann-Enskog多尺度展开技术对时间和空间导数, 分布函数
其中,
与一般的LBM相似, 把宏观物理量
由质量守恒定律,
由(2.7)式, 有
由(2.6)式, 有
为了恢复方程(1.3), 对平衡分布函数和修正函数做如下约束
对方程(2.7)两边关于
对方程(2.8)两边关于
其中
把(2.25)式, (2.26)式代入(2.24)式中
对方程(2.9)两边关于
其中
把(2.29)式, (2.30)式代入(2.28)式, 得到
采用LBM文献中所使用的符号,
为恢复宏观方程(1.3), 令
此时方程(2.32)为
为了推导出局部平衡态分布函数的具体表达式, 我们应该引入一个新的约束条件, 考虑到
其中引入参数
耦合方程(2.14)–(2.16). 假设速度1和速度2方向上的修正函数相同, 我们可以推导出补偿函数为
考虑到方程的系数为时变系数. 因此在具体的数值模拟时, 松弛时间
由文献[11], 把参数
为了确保本文建立的格子Boltzmann模型的稳定性, 因此必须保证松弛时间满足约束条件
对参数取值总结如下.
(1) 参数
(2) 常数
3 数值模拟
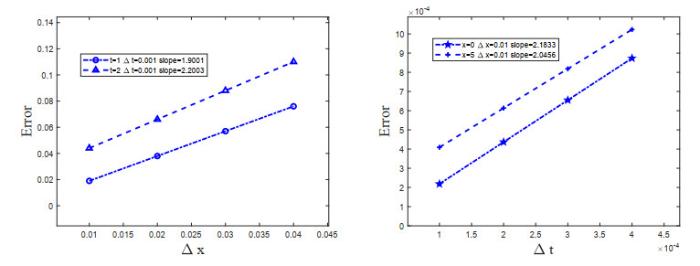
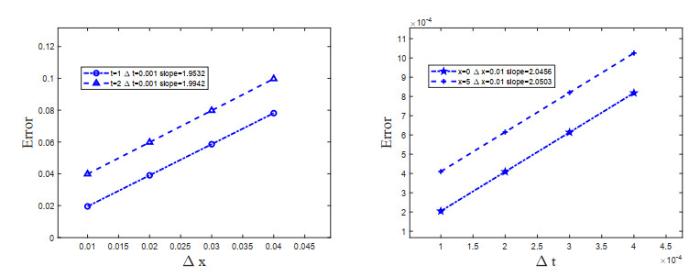
本文采用均方根误差
其中,
其中
算例3.1 取
它被用来描述流体中的波传播和分层内波传播现象, 以及等离子体中的离子声波. 令
其中,
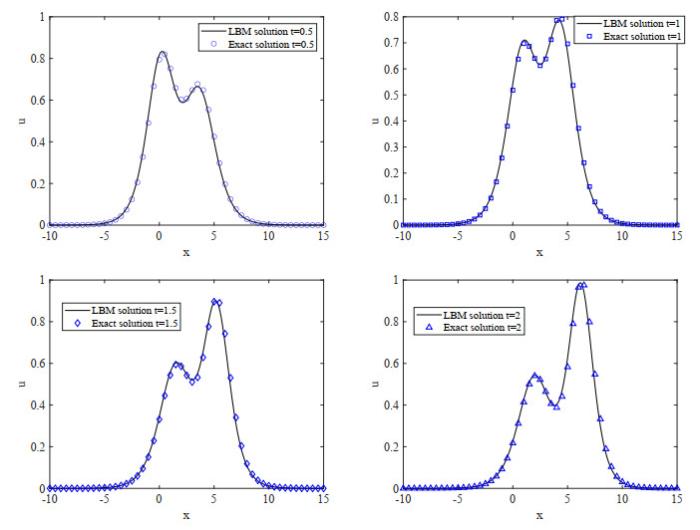
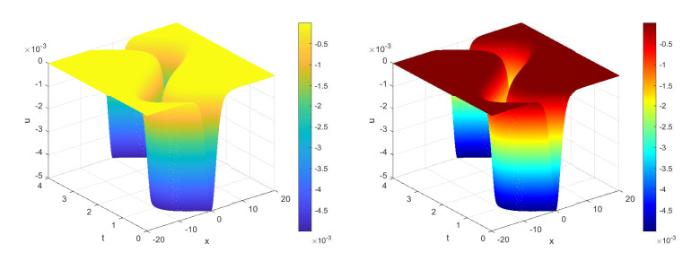
图 1
表 1 不同时刻方程(3.5)数值解与解析解比较分析
| Parameters | t=0.5 | t=1.0 | t=1.5 | t=2.0 |
| E2 | 5.1836e-04 | 4.9568e-04 | 6.1178e-04 | 7.6003e-04 |
| E∞ | 0.0364 | 0.0349 | 0.0478 | 0.0585 |
| GRE | 0.0334 | 0.0303 | 0.0369 | 0.0429 |
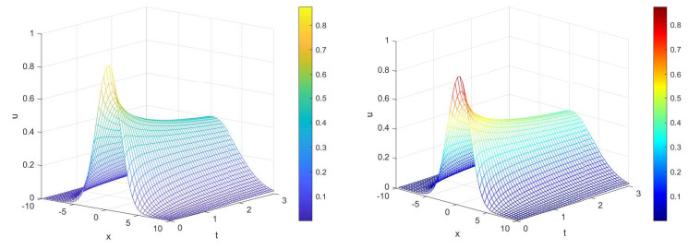
图 2
图 3
注3.1 数值模拟时, 为区分数值解与解析解, 用matlab中的colormap default表示数值解, colormap jet表示精确解, 下同.
算例3.2 取
初始条件和边界条件为
其中, 取
上式中, 取
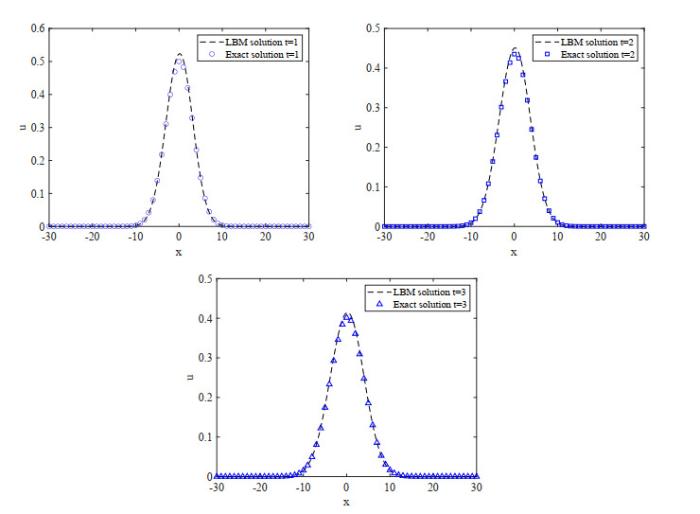
图 4
图 5
图 6
表 2 t = 1.0, 2.0, 3.0不同时刻方程(3.6)数值结果与解析解的比较
| Parameters | t=1.0 | t=2.0 | t=3.0 |
| E2 | 1.0660e-04 | 7.9380e-05 | 7.0678e-05 |
| E∞ | 0.0230 | 0.0151 | 0.0125 |
| GRE | 0.0343 | 0.0267 | 0.0252 |
算例3.3 考虑如下形式的广义变系数KdV-mKdV方程[15]
上式中, 取
表 3 t = 1.0, 2.0, 3.0不同时刻方程(3.7)数值解与解析解的对比分析
| Parameters | t=1.0 | t=2.0 | t=3.0 |
| E2 | 2.2805e-04 | 2.8858e-04 | 2.2420e-04 |
| E∞ | 0.0043 | 0.0055 | 0.0043 |
| GRE | 0.0593 | 0.0750 | 0.0583 |
图 7
图 8
图 9
4 结论
本文研究了一类变系数广义KdV-Burgers方程的格子Boltzmann模型. 首先, 通过选择平衡分布函数和适当地增加修正函数建立了方程(1.3). 利用D1Q5格子Boltzmann模型对不同形式的变系数KdV-Burgers方程进行数值模拟试验.其次, 证明了格子Boltzmann模型与宏观方程是相容的. 然后,引入自由参数
参考文献
Lattice Boltzmann method for fluid flows
DOI:10.1146/annurev.fluid.30.1.329 [本文引用: 1]
Equilibrium-type and link-type lattice Boltzmann models for generic advection and anisotropic-dispersion equation
DOI:10.1016/j.advwatres.2005.03.004 [本文引用: 1]
Lattice Boltzmann model for a class of convection-diffusionequations with variable coefficients
Lattice Boltzmann method for one and two-dimensional burgers equation
A lattice Boltzmann equation for waves
DOI:10.1006/jcph.2000.6486 [本文引用: 1]
A lattice Boltzmann model for the generalized Boussinesq equation
A unified lattice Boltzzmann model for some nonlinear partial differential equations
DOI:10.1016/j.chaos.2006.07.023 [本文引用: 1]
Multiple-relaxation-time lattice Boltzmann method for the Navier-Stokes and nonlinear convection-diffusion equations: modeling, analysis, and elements
Lattice Boltzmann model for a generalized Gardner equation with time-dependent variable coefficient
DOI:10.1016/j.apm.2017.01.061 [本文引用: 3]
General propagation lattice Boltzmann model for a variable-coefficient compound KdV-Burgers equation
DOI:10.1016/j.apm.2019.04.013 [本文引用: 3]
非线性偏微分方程的高阶格子BGK模型
A higer order lattice BGK model for simulating some nonlinear partial differential equations
Stability analysis of lattice Boltzmann methods
DOI:10.1006/jcph.1996.0016 [本文引用: 1]