长期以来, 传染病危害着人类的健康, 影响着经济的发展. 肺结核、乙肝、艾滋病等尚未根除, 新的传染病又相继爆发. 如2003年的非典(SARS)、2009年的甲型流感(H1N1)、2013年的禽流感(H7N9)对社会经济和人类健康造成了很大的影响. 众所周知, 近期的新型冠状病毒肺炎(COVID-19)由武汉首发并快速的向全国乃至周边各国蔓延, 人民群众的正常生活、社会经济遭受重大影响, 生命健康受到极大威胁^[1-2]. 近年来已有大量文献对传染病进行研究^[3-10].

研究传染病的经典数学模型是SIR模型, 该模型将人群分为三类: 易感者($ S $)、感染者($ I $)和治愈者($ R $). 易感者与感染者有效接触成为感染者, 在一段时间的治疗后成为治愈者. 随后, 国内外研究学者在此基础上对模型进行扩展, 考虑了新的仓室, 在易感者到感染者的环节中加入了潜伏者($ E $). 对于有些疾病, 潜伏期患者也具有明显的传染性^[11-12].

隔离是控制传染病的一种有效途径. 为了让模型更加符合疾病实际, 许多学者在模型中考虑了隔离措施^[13-15]. 文献[13]中提出了一类具有接种和隔离治疗的肺结核模型, 研究了模型的全局稳定性. 文献[14]中研究了易感人群软隔离行为对COVID-19在武汉的传播影响, 并评估了易感人群隔离率及易感人群暴露率对COVID-19疫情的影响. 文献[15]中研究了由确诊病例驱动跟踪隔离的时滞传染病数学模型, 重点讨论了有症状感染者和确诊病例驱动的追踪隔离措施在建模上的异同.

治疗也能够很好的控制传染病的流行, 但是对于个别传染病, 治疗可使症状消失, 但体内还可能存在病毒, 最终导致治疗失败^[16-17]. 文献[16]研究了两种治疗不完全的结核病模型. 假定受治疗的个体可能由于结核杆菌的残余进入潜伏期, 也可能由于治疗失败又回到感染者. 文献[17]提出了一类具有接种和不完全治疗的传染病模型, 确定了模型的基本再生数, 并证明了平衡点的全局稳定性.

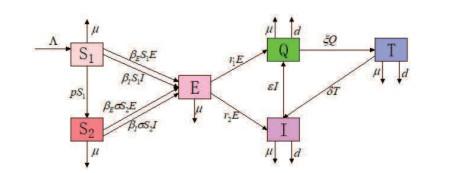
本文建立了一类具有隔离和不完全治疗的传染病模型, 并考虑了潜伏者的传染性. 模型中共有六个仓室: 无意识的易感者($ S_{1} $), 有意识的易感者($ S_{2} $), 潜伏者($ E $), 感染者($ I $), 隔离者($ Q $), 治疗者($ T $). 文中将易感者分为两类: 无意识的易感者和有意识的易感者, 他们接触患者的几率是不同的, 所以用$ \sigma $作为有意识的易感者接触率调节因子. 模型的参数定义见表 1, 模型的传播机制图见图 1.

根据模型的传播机制图得如下模型

(2.1) $ \begin{equation} \left\{\begin{array}{ll} {S_{1}}' = \Lambda-\beta_{E} S_{1}E-\beta_{I} S_{1}I-(p+\mu)S_{1}, \\ {S_{2}}' = pS_{1}-\beta_{E}\sigma S_{2}E-\beta_{I}\sigma S_{2}I-\mu S_{2}, \\ {E}' = \beta_{E}E( S_{1}+\sigma S_{2})+\beta_{I}I( S_{1}+\sigma S_{2})-(r_{1}+r_{2}+\mu)E, \\ {I}' = r_{2}E-(\mu+d+\varepsilon)I+\delta T, \\ {Q}' = r_{1}E+\varepsilon I-(\mu+d+\xi)Q, \\ {T}' = \xi Q-(\mu+d+\delta)T. \end{array}\right. \end{equation} $

模型中考虑的种群是人类, 给出模型的正性和不变集是非常重要的. 现将系统(2.1) 改写成矩阵的形式

(3.1) $ \begin{equation} {X}' = G(X), \end{equation} $

其中$ X = (S_{1}, S_{2}, E, I, Q, T)^{T}\in R^6 $.

(3.2) $ \begin{equation} G(X) = \left( \begin{array}{l} G_1(X) \\ G_2(X) \\ G_3(X) \\ G_4(X) \\ G_5(X) \\ G_6(X) \end{array} \right) = \left( \begin{array}{c} \Lambda-\beta_{E} S_{1}E-\beta_{I} S_{1}I-(p+\mu)S_{1}\\ pS_{1}-\beta_{E}\sigma S_{2}E-\beta_{I}\sigma S_{2}I-\mu S_{2}\\ \beta_{E}E( S_{1}+\sigma S_{2})+\beta_{I}I( S_{1}+\sigma S_{2})-(r_{1}+r_{2}+\mu)E\\ r_{2}E-(\mu+d+\varepsilon)I+\delta T \\ r_{1}E+\varepsilon I-(\mu+d+\xi)Q \\ \xi Q-(\mu+d+\delta)T \end{array} \right). \end{equation} $

容易得到

$ G_i(X)\mid _{X_i(t) = 0, X_t\in C_{+}}\geq 0, \quad \quad i = 1, 2, 3, 4, 5, 6. \label{2.4} $

根据文献[18]中的引理2可知, 对于任意的$ t\geq 0 $, 都有$ X(t)\in R_{+}^6 $.

对于系统(2.1), 不难得到

$ \begin{eqnarray*} {(S_{1}+S_{2}+E+I+Q+T)}' & = &\Lambda-\mu(S_{1}+S_{2}+E+I+Q+T)-d(I+Q+T)\\ &\leq&\Lambda-\mu(S_{1}+S_{2}+E+I+Q+T), \label{2.5} \end{eqnarray*} $

因此$ \lim\limits_{t\rightarrow +\infty }\sup [S_{1}(t)+S_{2}(t)+E(t)+I(t)+Q(t)+T(t)] \leq \frac \Lambda \mu $, 所以

$ \Omega = \Big\{(S_{1}, \;S_{2}, \;E, \;I, \;Q, \;T)\in \mathbb{R} _{+}^6:S_{1}+S_{2}+E+I+Q+T \leq \frac \Lambda \mu\Big\} \label{2.6} $

是系统(2.1) 的不变集. 我们将在不变集$ \Omega $上讨论系统(2.1) 的稳定性.

令系统(2.1) 的右端等于零, 则可以得到系统唯一的无病平衡点$ P^{0}(S_{1}^{0}, S_{2}^{0}, 0, 0, 0, 0) $, 其中

$ S_{1}^{0} = \frac{\Lambda}{p +\mu }, \qquad\qquad S_{2}^{0} = \frac{p\Lambda}{\mu(p +\mu )}. \label{3.1} $

下面利用基本再生矩阵的方法(参见文献[19]), 计算系统(2.1) 的基本再生数.

令$ x = (E, \;I, \;Q, \;T, \;S_{1}, \;S_{2})^T $, 系统(2.1) 可改写为

$ \frac{{\rm d}x}{{\rm d}t} = {\cal F}(x)-{\cal V}(x), \label{3.2} $

其中

(4.1) $ \begin{equation} \begin{array}{ll} {\cal F}(x) = \left( \begin{array}{c} \beta_{E}E( S_{1}+\sigma S_{2})+\beta_{I}I( S_{1}+\sigma S_{2}) \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} \right), \\ {\cal V}(x) = \left( \begin{array}{c} (r_{1}+r_{2}+\mu)E \\ (\mu+d+\varepsilon)I-r_{2}E-\delta T \\ (\mu+d+\xi)Q-r_{1}E-\varepsilon I\\ (\mu+d+\delta)T-\xi Q\\ \beta_{E} S_{1}E+\beta_{I} S_{1}I+(p+\mu)S_{1}-\Lambda\\ \beta_{E}\sigma S_{2}E+\beta_{I}\sigma S_{2}I+\mu S_{2}-pS_{1} \end{array} \right).\end{array} \end{equation} $

$ {\cal F}(x) $和$ {\cal V}(x) $在无病平衡点$ P^{0} $处的雅可比矩阵分别为

(4.2) $ \begin{equation} D{\cal F}(P^{0}) = \left( \begin{array}{cc} F_{4\times 4} & 0 \\ 0 & 0 \end{array} \right) , \qquad D{\cal V}(P^{0}) = \left( \begin{array}{ccc} V_{4\times 4} & 0 & 0 \\ \beta_{E}S_{1}^{0}\quad \beta_{I}S_{1}^{0}\quad 0 \quad 0 & p+\mu & 0 \\ \beta_{E}\sigma S_{2}^{0}\quad \beta_{I}\sigma S_{2}^{0}\quad 0 \quad 0 & -p & \mu \end{array} \right) , \end{equation} $

其中

$ F = \left( \begin{array}{cccc} \beta_{E}(S_{1}^{0}+\sigma S_{2}^{0}) & \beta_{I}(S_{1}^{0}+\sigma S_{2}^{0}) & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0& 0 \end{array} \right) , $

$ V = \left( \begin{array}{cccc} r_{1}+r_{2}+\mu & 0 & 0 & 0\\ -r_{2} & \mu+d+\varepsilon & 0 & -\delta\\ -r_{1} & -\varepsilon & \mu+d+\xi & 0\\ 0 & 0 & -\xi & \mu+d+\delta\\ \end{array} \right). $

则基本再生数为

(4.3) $ \begin{eqnarray} R_0& = &\rho (FV^{-1}) = \frac{\beta_{E}(S_{1}^{0}+\sigma S_{2}^{0})}{r_{1}+r_{2}+\mu}+\frac{[r_{2}(\mu+d+\xi)(\mu+d+\delta)+r_{1}\delta\xi]\beta_{I}(S_{1}^{0}+\sigma S_{2}^{0})}{(r_{1}+r_{2}+\mu)[(\mu+d+\varepsilon)(\mu+d+\xi)(\mu+d+\delta)-\varepsilon\delta\xi]} \\ & = &\frac{ \left.\begin{array}{c} (S_{1}^{0}+\sigma S_{2}^{0})\{\beta_{E}[(\mu+d+\varepsilon)(\mu+d+\xi)(\mu+d+\delta)-\varepsilon\delta\xi] \\ +\beta_{I}[r_{2}(\mu+d+\xi)(\mu+d+\delta)+r_{1}\delta\xi]\} \end{array}\right.} {(r_{1}+r_{2}+\mu)[(\mu+d+\varepsilon)(\mu+d+\xi)(\mu+d+\delta)-\varepsilon\delta\xi]} \\ & = &\frac{(S_{1}^{0}+\sigma S_{2}^{0})(\beta_{E}A+\beta_{I}B)}{(r_{1}+r_{2}+\mu)A}. \end{eqnarray} $

其中

(4.4) $ \begin{equation} A = (\mu+d+\varepsilon)(\mu+d+\xi)(\mu+d+\delta)-\varepsilon\delta\xi, \quad B = r_{2}(\mu+d+\xi)(\mu+d+\delta)+r_{1}\delta\xi. \end{equation} $

设$ P^{*}(S_{1}^{*}, S_{2}^{*}, E^{*}, I^{*}, Q^{*}, T^{*}) $为系统(2.1) 的地方病平衡点, 且满足下列方程

(4.5) $ \begin{equation} \left\{\begin{array}{ll} \Lambda-\beta_{E} S_{1}E-\beta_{I} S_{1}I-(p+\mu)S_{1} = 0, \\ pS_{1}-\beta_{E}\sigma S_{2}E-\beta_{I}\sigma S_{2}I-\mu S_{2} = 0, \\ \beta_{E}E( S_{1}+\sigma S_{2})+\beta_{I}I( S_{1}+\sigma S_{2})-(r_{1}+r_{2}+\mu)E = 0, \\ r_{2}E-(\mu+d+\varepsilon)I+\delta T = 0, \\ r_{1}E+\varepsilon I-(\mu+d+\xi)Q = 0, \\ \xi Q-(\mu+d+\delta)T = 0. \end{array}\right. \end{equation} $

由方程(4.5) 的前两个式子可得

(4.6) $ \begin{equation} S_{1} = \frac{\Lambda}{\beta_{E}E+\beta_{I}I+(p+\mu) }, \quad S_{2} = \frac{p\Lambda}{[\beta_{E}E+\beta_{I}I+(p+\mu)](\beta_{E}\sigma E+\beta_{I}\sigma I+\mu) }. \end{equation} $

由方程(4.5) 的最后一个式子可得

(4.7) $ \begin{equation} T = \frac \xi {\mu +d+\delta}Q. \end{equation} $

把(4.7) 式代入方程(4.5) 的第四式, 有

(4.8) $ \begin{equation} r_{2}E-(\mu+d+\varepsilon)I+\frac {\delta\xi} {\mu +d+\delta}Q = 0. \end{equation} $

由方程(4.5) 的第五个式子可得

(4.9) $ \begin{equation} Q = \frac{r_{1}E+\varepsilon I}{\mu+d+\xi}. \end{equation} $

把(4.9) 式代入(4.8) 式, 则有

(4.10) $ \begin{eqnarray} E = \frac{(\mu+d+\varepsilon)(\mu+d+\xi)(\mu+d+\delta)-\varepsilon\delta\xi} {r_{2}(\mu+d+\xi)(\mu+d+\delta)+r_{1}\delta\xi}I = \frac {A}{B}I. \end{eqnarray} $

因为$ I\neq0 $, 把(4.10) 式代入方程(4.5) 的第三式, 则

(4.11) $ \begin{equation} S_{1}+\sigma S_{2} = \frac {(r_{1}+r_{2}+\mu)A}{\beta_{E}A+\beta_{I}B} \end{equation} $

由(4.6) 和(4.10) 式可得

(4.12) $ \begin{eqnarray} S_{1}+\sigma S_{2}& = &\frac{\Lambda}{\beta_{E}E+\beta_{I}I+(p+\mu) }+\frac{\sigma p\Lambda}{[\beta_{E}E+\beta_{I}I+(p+\mu)](\beta_{E}\sigma E+\beta_{I}\sigma I+\mu) } \\ & = &\frac{\Lambda}{\beta_{E}E+\beta_{I}I+(p+\mu) }\cdot[1+\frac{\sigma p}{\sigma(\beta_{E} E+\beta_{I}I)+\mu }] \\ & = &\frac{\Lambda}{\beta_{E}E+\beta_{I}I+(p+\mu) }\cdot\frac{\sigma(\beta_{E} E+\beta_{I}I)+\mu+p\sigma}{\sigma(\beta_{E} E+\beta_{I}I)+\mu } \\ & = &\frac{\Lambda}{\frac{\beta_{E}A+\beta_{I}B}{B}I+(p+\mu) }\cdot\frac{\sigma\frac{\beta_{E}A+\beta_{I}B}{B}I+\mu+p\sigma}{\sigma\frac{\beta_{E}A+\beta_{I}B}{B}I+\mu } \\ & = &\frac{B\Lambda}{(\beta_{E}A+\beta_{I}B)I+(p+\mu)B }\cdot\frac{\sigma(\beta_{E}A+\beta_{I}B)I+(\mu+p\sigma)B}{\sigma(\beta_{E}A+\beta_{I}B)I+\mu B }. \end{eqnarray} $

将(4.11) 式代入(4.12) 式中, 有

(4.13) $ \begin{equation} H(I): = \frac{B[\sigma(\beta_{E}A+\beta_{I}B)I+(\mu+p\sigma)B]}{[(\beta_{E}A+\beta_{I}B)I+(p+\mu)B][\sigma(\beta_{E}A+\beta_{I}B)I+\mu B] } -\frac {(r_{1}+r_{2}+\mu)A}{(\beta_{E}A+\beta_{I}B)\Lambda} = 0. \end{equation} $

直接求导得

$ H^{^{\prime }}(I) = \frac{H_{1}(I)}{\{[(\beta_{E}A+\beta_{I}B)I+(p+\mu)B][\sigma(\beta_{E}A+\beta_{I}B)I+\mu B]\}^2}, $

令$ C = \beta_{E}A+\beta_{I}B $, 则

$ \begin{eqnarray*} H_{1}(I)& = &B\sigma(\beta_{E}A+\beta_{I}B)[(\beta_{E}A+\beta_{I}B)I+(p+\mu)B][\sigma(\beta_{E}A+\beta_{I}B)I+\mu B]\\ &&-B[\sigma(\beta_{E}A+\beta_{I}B)I+(\mu+p\sigma)B](\beta_{E}A+\beta_{I}B)\{[\sigma(\beta_{E}A+\beta_{I}B)I\\ & &+\mu B]+\sigma[(\beta_{E}A+\beta_{I}B)I+(p+\mu) B]\}\\ & = &\sigma BC[CI+(p+\mu)B][\sigma CI+\mu B]-BC[\sigma CI+(\mu+p\sigma) B]\{\sigma CI+\mu B\\ &&+\sigma[CI+(p+\mu)B]\}\\ & = &BC\{\sigma[CI+(p+\mu)B][\sigma CI+\mu B]-[\sigma CI+(\mu+p\sigma) B][\sigma CI+\mu B\\ &&+\sigma[CI+(p+\mu)B]]\}\\ & = &BC\{(\sigma\mu B-\mu B)(\sigma CI+\mu B)-[\sigma CI+(\mu+p\sigma) B]\sigma [CI+(p+\mu)B]\}\\ & = &-BC\{\mu B(\sigma CI+\mu B)+\sigma[\sigma C^2I^2+\sigma pBCI+C(\mu+p\sigma)BI\\ &&+[(\mu+p\sigma)p+p\sigma\mu]B^2]\}\\ & = &-BC\{(\sigma C)^2I^2+2\sigma BC(\mu+\sigma p)I+B^2[\mu^2+\mu p\sigma+p(p+\mu)\sigma^2]\}<0, \end{eqnarray*} $

故

$ H^{^{\prime }}(I)<0. $

所以$ H(I) $是关于$ I>0 $的单调递减函数. 由于

$ \begin{eqnarray*} &&[(\beta_{E}A+\beta_{I}B)I+(p+\mu)B][\sigma(\beta_{E}A+\beta_{I}B)I+\mu B]\\ &>&(\beta_{E}A+\beta_{I}B)I[\sigma(\beta_{E}A+\beta_{I}B)I+(\mu+p\sigma)B], \end{eqnarray*} $

则

$ H(I)<\frac B{(\beta_{E}A+\beta_{I}B)I}-\frac {(r_{1}+r_{2}+\mu)A}{(\beta_{E}A+\beta_{I}B)\Lambda}. $

又

$ \begin{eqnarray*} H(0) & = &\frac{\mu+p\sigma}{\mu(p+\mu)}-\frac {(r_{1}+r_{2}+\mu)A}{(\beta_{E}A+\beta_{I}B)\Lambda} = \frac{(S_{1}^{0}+\sigma S_{2}^{0})}\Lambda-\frac {(r_{1}+r_{2}+\mu)A}{(\beta_{E}A+\beta_{I}B)\Lambda} \\ & = &\frac{(\beta_{E}A+\beta_{I}B)(S_{1}^{0}+\sigma S_{2}^{0})-(r_{1}+r_{2}+\mu)A}{(\beta_{E}A+\beta_{I}B)\Lambda} \\ & = &\frac{(r_{1}+r_{2}+\mu)AR_0-(r_{1}+r_{2}+\mu)A}{(\beta_{E}A+\beta_{I}B)\Lambda} = \frac{(r_{1}+r_{2}+\mu)A}{(\beta_{E}A+\beta_{I}B)\Lambda}(R_{0}-1), \end{eqnarray*} $

且

$ \begin{eqnarray*} &&H(\frac{\Lambda}\mu)<\frac {\mu B}{(\beta_{E}A+\beta_{I}B)\Lambda}-\frac {(r_{1}+r_{2}+\mu)A}{(\beta_{E}A+\beta_{I}B)\Lambda}\\ & = &\frac {\mu B-(r_{1}+r_{2}+\mu)A}{(\beta_{E}A+\beta_{I}B)\Lambda} \\ & = &\{\mu[r_{2}(\mu+d+\xi)(\mu+d+\delta)+r_{1}\delta\xi]- (r_{1}+r_{2}+\mu)[(\mu+d+\varepsilon)(\mu+d+\xi)(\mu+d+\delta)\\ & &-\varepsilon\delta\xi]\}/\{(\beta_{E}A+\beta_{I}B)\Lambda\} \\ & = &\frac {(\mu+d+\xi)(\mu+d+\delta)[\mu r_{2}-(r_{1}+r_{2}+\mu)(\mu+d+\varepsilon)]+ \mu r_{1}\delta\xi+(r_{1}+r_{2}+\mu)\varepsilon\delta\xi}{(\beta_{E}A+\beta_{I}B)\Lambda} \\ & = &-\frac {(\mu+d+\xi)(\mu+d+\delta)[(r_{1}+r_{2}+\mu)(d+\varepsilon)+ (r_{1}+\mu)\mu]-\mu r_{1}\delta\xi-(r_{1}+r_{2}+\mu)\varepsilon\delta\xi}{(\beta_{E}A+\beta_{I}B)\Lambda} \\ & = &-\{[(\mu+d)(\mu+d+\xi+\delta)+\delta\xi][(r_{1}+r_{2}+\mu)(d+\varepsilon)+ (r_{1}+\mu)\mu]\\ & &-\delta\xi[\mu r_{1}+(r_{1}+r_{2}+\mu)\varepsilon]\}/\{(\beta_{E}A+\beta_{I}B)\Lambda\} \\ & = &-\frac {(\mu+d)(\mu+d+\xi+\delta)[(r_{1}+r_{2}+\mu)(d+\varepsilon)+ (r_{1}+\mu)\mu]+\delta\xi[(r_{1}+r_{2}+\mu)d+\mu^2]}{(\beta_{E}A+\beta_{I}B)\Lambda} \\ &<&0. \end{eqnarray*} $

由函数$ H(I) $的单调性可知, 当$ R_{0}>1 $时, 方程(4.13) 在区间$ (0, \frac{\Lambda}\mu) $上存在唯一的正根. 当$ R_{0}\leq1 $时, 方程(4.13) 在区间$ (0, \frac{\Lambda}\mu) $上不存在正根. 综上, 有如下结论.

定理4.1 对于系统(2.1), 总存在一个无病平衡点$ P^{0}(S_{1}^{0}, S_{2}^{0}, 0, 0, 0, 0) $. 当$ R_{0}>1 $, 除无病平衡点$ P^{0} $外, 系统(2.1) 还存在唯一的地方病平衡点$ P^{*}(S_{1}^{*}, S_{2}^{*}, E^{*}, I^{*}, Q^{*}, T^{*}) $, 其中

$ S_{1}^{*} = \frac{B\Lambda }{(\beta_{E}A+\beta_{I}B)I^{*}+(p+\mu)B}, $

$ S_{2}^{*} = \frac{p \Lambda B^2}{[(\beta_{E}A+\beta_{I}B)I^{*}+(p+\mu)B][(\beta_{E}A+\beta_{I}B)\sigma I^{*}+\mu B]}, $

$ E^{*} = \frac A BI^{*}, Q^{*} = \frac{Ar_{1}+B\varepsilon }{(\mu+d+\xi)B}I^{*}, T^{*} = \frac{\xi(Ar_{1}+B\varepsilon) }{(\mu+d+\xi)(\mu+d+\xi)B}I^{*} $

$ I^{*} $是方程$ H(I) = 0 $的唯一正根.

定理5.1 对于系统(2.1), 当$ R_{0}\leq1 $时, 无病平衡点$ P^{0} $是全局渐近稳定的.

证  无病平衡点$ P^{0}(S_{1}^{0}, S_{2}^{0}, 0, 0, 0, 0) $中$ S_{1}^{0} $和$ S_{2}^{0} $满足下列方程

(5.1) $ \begin{equation} \left\{\begin{array}{ll} \Lambda-\beta_{E} S_{1}E-\beta_{I} S_{1}I-(p+\mu)S_{1} = 0, \\ pS_{1}-\beta_{E}\sigma S_{2}E-\beta_{I}\sigma S_{2}I-\mu S_{2} = 0, \end{array}\right. \end{equation} $

则系统(2.1) 可被改写为

(5.2) $ \begin{equation} \left\{\begin{array}{ll} {S_{1}}' = S_{1}[\Lambda(\frac 1{S_{1}}-\frac 1{S_{1}^{0}})-\beta_{E}E-\beta_{I}I], \\ {S_{2}}' = S_{2}[p(\frac {S_{1}}{S_{2}}-\frac {S_{1}^{0}}{S_{2}^{0}})-\beta_{E}\sigma E-\beta_{I}\sigma I], \\ {E}' = (\beta_{E}E+\beta_{I}I)[(S_{1}^{0}+\sigma S_{2}^{0})+( S_{1}-S_{1}^{0})+\sigma (S_{2}-S_{2}^{0})]-(r_{1}+r_{2}+\mu)E, \\ {I}' = r_{2}E-(\mu+d+\varepsilon)I+\delta T, \\ {Q}' = r_{1}E+\varepsilon I-(\mu+d+\xi)Q, \\ {T}' = \xi Q-(\mu+d+\delta)T. \end{array}\right. \end{equation} $

定义Lyapunov函数

(5.3) $ \begin{equation} V_{1} = (S_{1}-S_{1}^{0}-S_{1}^{0}\ln \frac {S_{1}}{S_{1}^{0}})+(S_{2}-S_{2}^{0}-S_{2}^{0}\ln \frac {S_{2}}{S_{2}^{0}})+ E+ D_{1}I+D_{2}Q+D_{3}T. \end{equation} $

其中

$ D_{1} = \frac {[(r_{1}+r_{2}+\mu)-\beta_{E}(S_{1}^{0}+\sigma S_{2}^{0})](\mu+d+\xi)(\mu+d+\delta)}B, \nonumber $

$ D_{2} = \frac {[(r_{1}+r_{2}+\mu)-\beta_{E}(S_{1}^{0}+\sigma S_{2}^{0})]\delta\xi}B, \nonumber $

$ D_{3} = \frac {[(r_{1}+r_{2}+\mu)-\beta_{E}(S_{1}^{0}+\sigma S_{2}^{0})](\mu+d+\xi)\delta}B. $

$ V_{1} $沿系统(2.1) 的全导数为

(5.4) $ \begin{eqnarray} {V_{1}}'& = &(S_{1}-S_{1}^{0})[\Lambda(\frac 1{S_{1}}-\frac 1{S_{1}^{0}}) -\beta_{E}E-\beta_{I}I]+(S_{2}-S_{2}^{0})[p(\frac {S_{1}}{S_{2}}-\frac {S_{1}^{0}}{S_{2}^{0}})\\ &&-\beta_{E}\sigma E-\beta_{I}\sigma I]+(\beta_{E}E+\beta_{I}I)[(S_{1}^{0}+\sigma S_{2}^{0})+( S_{1}-S_{1}^{0}) +\sigma (S_{2}-S_{2}^{0})]\\ &&-(r_{1}+r_{2}+\mu)E+D_{1}[r_{2}E-(\mu+d+\varepsilon)I+\delta T] \\ &&+D_{2}[r_{1}E+\varepsilon I-(\mu+d+\xi)Q]+D_{3}[\xi Q-(\mu+d+\delta)T] \\ & = &[\beta_{I}(S_{1}^{0}+\sigma S_{2}^{0})-(\mu+d+\varepsilon)D_{1}+\varepsilon D_{2}]I+F(S, I) \\ & = &\frac{(r_{1}+r_{2}+\mu)A}B(R_{0}-1)I+F(S, I), \end{eqnarray} $

其中

$ F(S, I) = \Lambda(S_{1}-S_{1}^{0})(\frac 1{S_{1}}-\frac 1{S_{1}^{0}})+p(S_{2}-S_{2}^{0})(\frac {S_{1}}{S_{2}}-\frac {S_{1}^{0}}{S_{2}^{0}}). $

令$ x = \frac {S_{1}}{S_{1}^{0}}, \;y = \frac {S_{2}}{S_{2}^{0}} $, 则

(5.5) $ \begin{equation} F(S, I) = \Lambda (x-1)(\frac 1x-1)+pS_{1}^{0}(y-1)(\frac xy-1) = :\overline{F}(x, y). \end{equation} $

结合(5.2) 式, 函数$ \overline{F}(x, y) $可写为

(5.6) $ \begin{eqnarray} \overline{F}(x, y)& = &\Lambda(2-x-\frac 1x)+pS_{1}^{0}(x-y-\frac x y+1) \\ & = &(2\Lambda+pS_{1}^{0})-(\Lambda-pS_{1}^{0})x-\Lambda\frac 1x-pS_{1}^{0}y-pS_{1}^{0}\frac x y \\ & = &3pS_{1}^{0}+2\mu S_{1}^{0}-\mu S_{1}^{0}x-(pS_{1}^{0}+\mu S_{1}^{0})\frac 1x-pS_{1}^{0}y-pS_{1}^{0}\frac x y \\ & = &pS_{1}^{0}(3-\frac 1x-y-\frac x y)+\mu S_{1}^{0}(2-x-\frac 1x). \end{eqnarray} $

故当$ x, y>0 $时, $ \overline{F}(x, y)\leq0 $, 当且仅当$ x = y = 1 $时, $ \overline{F}(x, y) = 0 $. 因此当$ R_{0}\leq 1 $时, $ {V_{1}}'\leq0 $. 由LaSalle不变集原理(参见文献[20])可知, 当$ R_{0}\leq1 $时, 无病平衡点$ P^{0} $是全局渐近稳定的. 证毕.

定理5.2  对于系统(2.1), 当$ R_{0}>1 $时, 地方病平衡点$ P^{*} $是全局渐近稳定的.

证  地方病平衡点$ P^{*}(S_{1}^{*}, S_{2}^{*}, E^{*}, I^{*}, Q^{*}, T^{*}) $满足下列方程

(5.7) $ \begin{equation} \left\{\begin{array}{ll} \Lambda-\beta_{E} S_{1}E-\beta_{I} S_{1}I-(p+\mu)S_{1} = 0, \\ pS_{1}-\beta_{E}\sigma S_{2}E-\beta_{I}\sigma S_{2}I-\mu S_{2} = 0, \\ \beta_{E}E( S_{1}+\sigma S_{2})+\beta_{I}I( S_{1}+\sigma S_{2})-(r_{1}+r_{2}+\mu)E = 0, \\ r_{2}E-(\mu+d+\varepsilon)I+\delta T = 0, \\ r_{1}E+\varepsilon I-(\mu+d+\xi)Q = 0, \\ \xi Q-(\mu+d+\delta)T = 0. \end{array}\right. \end{equation} $

记

$ \frac {S_{1}}{S_{1}^{*}} = x, \quad \quad \frac {S_{2}}{S_{2}^{*}} = y, \quad \quad \frac E{E^{*}} = z, \quad \quad \frac I{I^{*}} = u, \quad \quad \frac Q{Q^{*}} = v \quad \quad \frac T{T^{*}} = w, $

系统(2.1) 可被改写为

(5.8) $ \begin{equation} \left\{\begin{array}{ll} {x}' = x[\frac {\Lambda}{S_{1}^{*}}(\frac 1{x}-1)-\beta_{E}E^{*}(z-1)-\beta_{I}I^{*}(u-1)], \\ {y}' = y[\frac {pS_{1}^{*}}{S_{2}^{*}}(\frac xy-1)-\beta_{E}\sigma E^{*}(z-1)-\beta_{I}\sigma I^{*}(u-1)], \\ {z}' = z\{\beta_{E}[S_{1}^{*}(x-1)+\sigma S_{2}^{*}(y-1)]+\frac {\beta_{I}I^{*}}{E^{*}}[S_{1}^{*}(\frac {xu}{z}-1)+\sigma S_{2}^{*}(\frac {yu}{z}-1)]\}, \\ {u}' = u[\frac {r_{2}E^{*}}{I^{*}}(\frac zu-1)+\frac {\delta T^{*}}{I^{*}}(\frac wu-1)], \\ {v}' = v[\frac {r_{1}E^{*}}{Q^{*}}(\frac zv-1)+\frac {\varepsilon I^{*}}{Q^{*}}(\frac uv-1)], \\ {w}' = w[\frac {\xi Q^{*}}{T^{*}}(\frac vw-1)]. \end{array}\right. \end{equation} $

定义Lyapunov函数

(5.9) $ \begin{eqnarray} V_{2}& = &S_{1}^{*}(x-1-\ln x)+S_{2}^{*}(y-1-\ln y)+E^{*}(z-1-\ln z)+F_{1} I^{*}(u-1-\ln u) \\ &&+F_{2} Q^{*}(v-1-\ln v)+F_{3} T^{*}(w-1-\ln w). \end{eqnarray} $

$ V_{2} $沿系统(2.1) 的全导数为

(5.10) $ \begin{eqnarray} {V_{2}}'& = &S_{1}^{*}\frac {x-1}{x}{x}'+S_{2}^{*}\frac {y-1}{y}{y}' +E^{*}\frac {z-1}{z}{z}'+F_{1} I^{*}\frac {u-1}{u}{u}'+F_{2} Q^{*}\frac {v-1}{v}{v}'+F_{3}T^{*}\frac {w-1}{w}{w}'\\ & = &(x-1)[\Lambda(\frac 1{x}-1)-\beta_{E}S_{1}^{*}E^{*}(z-1)-\beta_{I}S_{1}^{*}I^{*}(u-1)]\\ &&+(y-1)[pS_{1}^{*}(\frac xy-1)-\beta_{E}\sigma S_{2}^{*} E^{*}(z-1)-\beta_{I}\sigma S_{2}^{*} I^{*}(u-1)]\\ &&+(z-1)\{\beta_{E}E^{*}[S_{1}^{*}(x-1)+\sigma S_{2}^{*}(y-1)]+\beta_{I}I^{*}[S_{1}^{*}(\frac {xu}{z}-1)+\sigma S_{2}^{*}(\frac {yu}{z}-1)]\}\\ &&+F_{1}(u-1)[r_{2}E^{*}(\frac zu-1)+\delta T^{*}(\frac wu-1)]\\ &&+F_{2}(v-1)[r_{1}E^{*}(\frac zv-1)+\varepsilon I^{*}(\frac uv-1)]+F_{3}(w-1)[\xi Q^{*}(\frac vw-1)]\\ & = &\Lambda(x-1)(\frac 1{x}-1)-\beta_{I}S_{1}^{*}I^{*}(x-1)(u-1)+pS_{1}^{*}(y-1)(\frac xy-1)\\ & &-\beta_{I}\sigma S_{2}^{*} I^{*}(y-1)(u-1)+\beta_{I}S_{1}^{*}I^{*}(z-1)(\frac {xu}{z}-1)+\beta_{I}\sigma S_{2}^{*}I^{*}(z-1)(\frac {yu}{z}-1)\\ &&+F_{1}r_{2}E^{*}(u-1)(\frac zu-1)+F_{1}\delta T^{*}(u-1)(\frac wu-1)\\ &&+F_{2}r_{1}E^{*}(v-1)(\frac zv-1)+F_{2}\varepsilon I^{*}(v-1)(\frac uv-1)+F_{3}\xi Q^{*}(w-1)(\frac vw-1)\\ & = &\Lambda(2-x-\frac 1{x})-\beta_{I}S_{1}^{*}I^{*}(xu-x-u-1)+pS_{1}^{*}(x-y-\frac xy+1)\\ &&-\beta_{I}\sigma S_{2}^{*} I^{*}(yu-y-u+1)+\beta_{I}S_{1}^{*}I^{*}(xu-z-\frac {xu}{z}+1)\\ &&+\beta_{I}\sigma S_{2}^{*}I^{*}(yu-z-\frac {yu}{z}+1)+F_{1}r_{2}E^{*}(z-u-\frac zu+1)+F_{1}\delta T^{*}(w-u-\frac wu+1)\\ &&+F_{2}r_{1}E^{*}(z-v-\frac zv+1)+F_{2}\varepsilon I^{*}(u-v-\frac uv+1)+F_{3}\xi Q^{*}(v-w-\frac vw+1)\\ & = &2\Lambda+pS_{1}^{*}+F_{1}r_{2}E^{*}+F_{1}\delta T^{*}+F_{2}r_{1}E^{*}+F_{2}\varepsilon I^{*}+F_{3}\xi Q^{*}-x(\Lambda-\beta_{I}S_{1}^{*}I^{*}-pS_{1}^{*})\\ &&-\Lambda\frac 1{x}-y(pS_{1}^{*}-\beta_{I}\sigma S_{2}^{*} I^{*})+z(-\beta_{I}S_{1}^{*}I^{*}-\beta_{I}\sigma S_{2}^{*}I^{*}+F_{1}r_{2}E^{*}+F_{2}r_{1}E^{*})\\ &&+u(\beta_{I}S_{1}^{*}I^{*}+\beta_{I}\sigma S_{2}^{*}I^{*}-F_{1}r_{2}E^{*}-F_{1}\delta T^{*}+F_{2}\varepsilon I^{*})\\ &&+v(-F_{2}r_{1}E^{*}-F_{2}\varepsilon I^{*}+F_{3}\xi Q^{*})+w(F_{1}\delta T^{*}-F_{3}\xi Q^{*})-pS_{1}^{*}\frac xy-\beta_{I}S_{1}^{*}I^{*}\frac {xu}{z}\\ &&-\beta_{I}\sigma S_{2}^{*}I^{*}\frac {yu}{z}-F_{1}r_{2}E^{*}\frac zu-F_{1}\delta T^{*}\frac wu-F_{2}r_{1}E^{*}\frac zv-F_{2}\varepsilon I^{*}\frac uv -F_{3}\xi Q^{*}\frac vw . \end{eqnarray} $

在(5.10) 式中, 只有变量$ z $, $ u $, $ v $和$ w $的系数可能为正. 若这些系数全为正, 那么$ {V_{2}}' $才有可能为正. 所以令$ z $, $ u $, $ v $和$ w $的系数全为$ 0 $, 则有

(5.11) $ \begin{equation} \left\{\begin{array}{ll} -\beta_{I}S_{1}^{*}I^{*}-\beta_{I}\sigma S_{2}^{*}I^{*}+F_{1}r_{2}E^{*}+F_{2}r_{1}E^{*} = 0, \\ \beta_{I}S_{1}^{*}I^{*}+\beta_{I}\sigma S_{2}^{*}I^{*}-F_{1}r_{2}E^{*}-F_{1}\delta T^{*}+F_{2}\varepsilon I^{*} = 0, \\ -F_{2}r_{1}E^{*}-F_{2}\varepsilon I^{*}+F_{3}\xi Q^{*} = 0, \\ F_{1}\delta T^{*}-F_{3}\xi Q^{*} = 0. \end{array}\right. \end{equation} $

从上式可以分别求出

$ F_{1} = \frac {\beta_{I}(r_{1}+r_{2}+\mu)(\mu+d+\xi)(\mu+d+\delta)}{\beta_{E}A+\beta_{I}B}, \nonumber $

$ F_{2} = \frac {\beta_{I}\delta\xi(r_{1}+r_{2}+\mu)}{\beta_{E}A+\beta_{I}B}, F_{3} = \frac {\beta_{I}\delta(r_{1}+r_{2}+\mu)(\mu+d+\xi)}{\beta_{E}A+\beta_{I}B}. $

因此可得

(5.12) $ \begin{eqnarray} {V_{2}}'& = &2\Lambda+pS_{1}^{*}+F_{1}r_{2}E^{*}+F_{1}\delta T^{*}+F_{2}r_{1}E^{*}+F_{2}\varepsilon I^{*}+F_{3}\xi Q^{*}-x(\Lambda-\beta_{I}S_{1}^{*}I^{*}-pS_{1}^{*})\\ &&-\Lambda\frac 1{x}-y(pS_{1}^{*}-\beta_{I}\sigma S_{2}^{*} I^{*})-pS_{1}^{*}\frac xy-\beta_{I}S_{1}^{*}I^{*}\frac {xu}{z} -\beta_{I}\sigma S_{2}^{*}I^{*}\frac {yu}{z}\\ & &-F_{1}r_{2}E^{*}\frac zu-F_{1}\delta T^{*}\frac wu-F_{2}r_{1}E^{*}\frac zv-F_{2}\varepsilon I^{*}\frac uv -F_{3}\xi Q^{*}\frac vw \\ & = &(\Lambda-\beta_{I}S_{1}^{*}I^{*}-pS_{1}^{*})(2-x-\frac 1{x})+(pS_{1}^{*}-\beta_{I}\sigma S_{2}^{*}I^{*})(3-\frac 1{x}-y-\frac xy)\\ &&+(\beta_{I}S_{1}^{*}I^{*}-\frac {\beta_{I}r_{1}\delta\xi(r_{1}+r_{2}+\mu)}{\beta_{E}A+\beta_{I}B}E^{*})(3-\frac 1{x}-\frac {xu}{z}-\frac zu) \\ &&+\beta_{I}\sigma S_{2}^{*}I^{*}(4-\frac 1{x}-\frac xy-\frac {yu}{z}-\frac zu)+\frac {\beta_{I}\varepsilon\delta\xi(r_{1}+r_{2}+\mu)}{\beta_{E}A+\beta_{I}B} I^{*}(3-\frac wu-\frac uv-\frac vw)\\ & &+\frac {\beta_{I}r_{1}\delta\xi(r_{1}+r_{2}+\mu)}{\beta_{E}A+\beta_{I}B}E^{*}(5-\frac 1{x}-\frac {xu}{z}-\frac wu-\frac zv-\frac vw) . \end{eqnarray} $

根据算术平均数与几何平均数之间的关系可知, 当$ x>0 $时, $ 2-x-\frac 1x\leq0 $, 当且仅当$ x = 1 $时, $ 2-x-\frac 1x = 0 $; 当$ x, y>0 $时, $ 3-\frac 1{x}-y-\frac xy\leq0 $, 当且仅当$ x = y = 1 $时, $ 3-\frac 1{x}-y-\frac xy = 0 $; 当$ x, z, u>0 $时, $ 3-\frac 1x-\frac{xu}z-\frac zu\leq0 $, 当且仅当$ x = 1, z = u $时, $ 3-\frac 1x-\frac{xu}z-\frac zu = 0 $; 当$ x, y, z, u>0 $时, $ 4-\frac 1{x}-\frac xy-\frac {yu}{z}-\frac zu\leq0 $, 当且仅当$ x = y = 1, z = u $时, $ 4-\frac 1{x}-\frac xy-\frac {yu}{z}-\frac zu = 0 $; 当$ u, v, w>0 $时, $ 3-\frac wu-\frac uv-\frac vw\leq0 $, 当且仅当$ u = v = w $时, $ 3-\frac wu-\frac uv-\frac vw = 0 $; 当$ x, z, u, v, w>0 $时, $ 5-\frac 1{x}-\frac {xu}{z}-\frac wu-\frac zv-\frac vw\leq0 $, 当且仅当$ x = 1, z = u = v = w $时, $ 5-\frac 1{x}-\frac {xu}{z}-\frac wu-\frac zv-\frac vw = 0 $. 所以当$ x, y, z, u, v, w>0 $时, $ {V_{2}}'\leq0 $, 当且仅当$ x = y = 1, z = u = v = w $时, $ {V_{2}}' = 0 $. 系统(2.1) 在$ \{(x, y, z, u, v, w):{V_{2}}' = 0\} $中的最大不变集为$ (1, 1, 1, 1, 1, 1) $. 由LaSalle不变集原理(参见文献[20])可知, 当$ R_{0}>1 $时, 系统(2.1) 的地方病平衡点$ P^{*} $是全局渐近稳定的. 证毕.

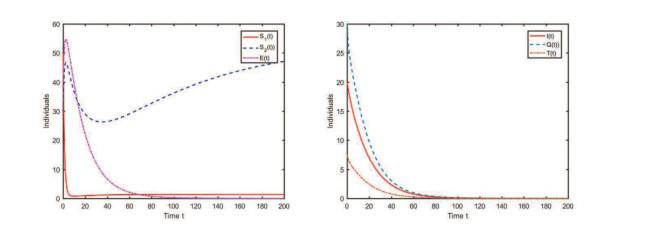
为了进一步解释说明前面得到的结论, 下面进行数值模拟. 选取的参数如下: $ \Lambda = 0.55 $, $ \mu = 0.01 $, $ p = 0.4 $, $ \beta_{E} = 0.007 $, $ \beta_{I} = 0.003 $, $ \sigma = 0.1 $, $ r_{2} = 0.01 $, $ \delta = 0.001 $, $ \xi = 0.25 $, $ d = 0.0053 $. 首先, 选取$ r_{1} = 0.06 $, $ \varepsilon = 0.07 $, 数值模拟显示当$ R_0 = 0.6286<1 $时, 无病平衡点$ P^{0} $是全局渐近稳定的(图 2). 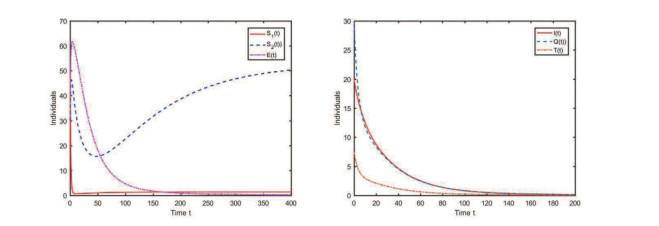其次, 选取$ r_{1} = 0.0299 $, $ \varepsilon = 0.07 $, 数值模拟显示当$ R_0 = 1 $时, 无病平衡点$ P^{0} $是全局渐近稳定的(图 3). 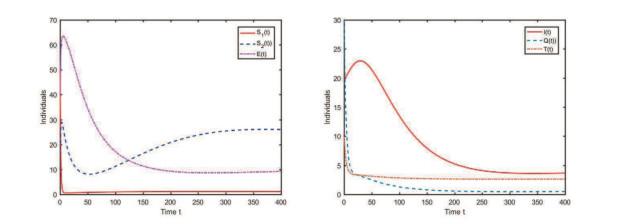最后, 选取$ r_{1} = 0.01 $, $ \varepsilon = 0.01 $, 数值模拟显示当$ R_0 = 1.852>1 $时, 地方病平衡点$ P^{*} $是全局渐近稳定的(图 4).

本文建立了一类具有隔离和不完全治疗的传染病模型, 并研究了传染病的动力学行为. 通过再生矩阵的方法, 我们确定了模型的基本再生数$ R_{0} $, 它在控制传染病的传播中起着至关重要的作用. 通过构造Lyapunov函数, 我们证明了平衡点的全局稳定性. 当$ R_{0}\leq1 $时, 无病平衡点$ P^{0} $是全局渐近稳定的, 即疾病最终消除; 当$ R_{0}>1 $时, 地方病平衡点$ P^{*} $是全局渐近稳定的, 也就是说, 这种疾病将持续存在.

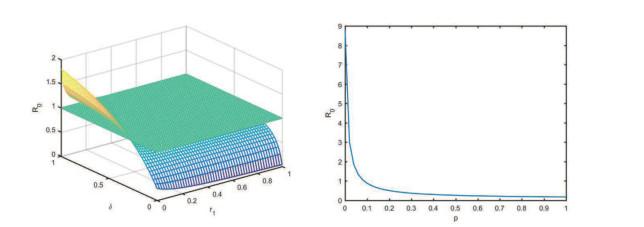
文中前面给出了基本再生数$ R_{0} $的表达式, 即

$ \begin{eqnarray*} R_0& = &\{\Lambda(\mu+\sigma p)\{\beta_{E}[(\mu+d+\varepsilon)(\mu+d+\xi)(\mu+d+\delta)-\varepsilon\delta\xi] \\ &&+\beta_{I}[r_{2}(\mu+d+\xi)(\mu+d+\delta)+r_{1}\delta\xi]\}\}\\ &&/ \{\mu(p+\mu)(r_{1}+r_{2}+\mu)[(\mu+d+\varepsilon)(\mu+d+\xi)(\mu+d+\delta)-\varepsilon\delta\xi]\}. \end{eqnarray*} $

从这个表达式中, 我们可以看出$ R_0 $是关于$ r_{1} $和$ \delta $的函数. 图 5(a)显示, 随着$ r_1 $的增大, $ R_0 $在减小; 随着$ \delta $的减小, $ R_0 $在减小. 这也说明, 加大对患者的隔离, 增强治疗的效果, 可以有效的控制疾病. 图 5(b)显示, 随着$ p $的增大, $ R_0 $在减小. 这也说明, 大力的宣传防控知识, 让民众对疾病有所认识, 可以有效的预防疾病.