1 引言
近年来许多学者对保险公司的最优投资和再保险问题进行了研究, 见文献[1-4]. 上述文献是在确定保险市场及金融市场模型的基础上研究的. 也就是说, 投资者对保险市场和风险资产价格的演变和分布有一定的把握. 这是不现实的. 由于保险及金融市场存在多种不可控风险和信息技术的有限性, 所以保险公司会对保险及金融市场存在模糊性. 这里的模糊性指的是概率测度的模糊性, 即构建保险市场和金融市场模型时的概率测度(一般称为参考概率) 存在某些不可避免的偏差. 那么需要我们找到合理的概率测度(一般称为替代概率) 来代替参考概率. 模糊厌恶优化问题的早期工作, 例如文献[5] 研究了模糊厌恶下期望效用最大化的最优投资消费. 文献[6] 也通过控制方法来研究模糊厌恶下有限水平效用最大化问题. 文献[7-8]研究模糊厌恶下最大化保险公司的终端财富期望效用, 得出保险公司最优投资和保费策略的解析解. 文献[9] 研究了模糊厌恶下的最小化个人生存破产概率, 其中假设个人的死亡时间服从一个指数分布, 目标函数是最小化个人生存破产概率, 得到了模糊厌恶下最优鲁棒投资策略. 该文从一个全新的角度分析了模型不确定对投资决策的影响, 给我们研究模糊问题提供了一个全新的思路.
最小化破产概率是另一个重要的研究课题, 并且在过去几十年中得到了广泛研究, 例如文献[10-12]. 这些文献及其参考文献大多对破产概率最小化问题进行各种研究. 但在实际的金融市场中, 投资者更喜欢将其盈余过程的价值维持在某一确定的正水平, 或者更高水平比如迄今为止最大价值的固定比例. 因此产生了最小drawdown概率, 即盈余过程的价值下降到迄今为止其最大值的固定比例以下的概率. 最近, 文献[13-14]研究了无限期范围内的最小drawdown概率问题, 并表明如果drawdown不发生, 最小破产概率的最优策略也将drawdown概率最小化. 此外, 文献[15] 也研究了终生投资问题, 旨在最小化drawdown发生的风险, 发现针对生命周期下降的最优策略和相应的破产问题与前者明显不同. 文献[16] 研究了危险区间和安全区间保险公司的投资再保问题, 得出危险区间的最小drawdown概率.
受上述文献启发, 本文以最小drawdown概率为研究目标, 研究模糊厌恶下的最优鲁棒投资和再保险. 我们应用最优控制理论解决最优问题, 得到最优鲁棒投资和再保险策略的解析解, 以及相应鲁棒情形下的最小drawdown概率. 本文的其余部分安排如下, 在第二节介绍模型和优化问题; 第三节主要是给出优化问题的验证定理, 对模糊厌恶优化问题进行求解; 第四节讨论解析解的规律性质;第五节利用几个数值例子分析不同参数对最小drawdown概率和漂移扭曲的影响; 最后是结论和展望.
2 模型设定
2.1 保险金融市场的模型假设
假设带漂移的Brown运动服从分布
其中
其中
假设金融市场存在一个无风险资产和一个风险资产且无风险资产的价格过程为
其中
其中
另允许保险公司购买比例再保险,
设
定义2.1 设
则称
2.2 Drawdown概率
定义
其中
即保险公司的盈余首次跌至或低于
如果盈余价值不低于
2.3 保险金融市场的模糊性与目标函数
概率测度
记
由于
其中
是一个域流
根据Girsanov定理, 测度
其中
我们将(2.12)-(2.13) 式代入到(2.4) 式得到测度
为了考虑替代概率测度
由于
其中
本文的目的是在鲁棒意义下使保险公司的盈余跌至或低于
下标
将
定义2.2 (鲁棒值函数)
3 模糊厌恶下的最小Drawdown概率
当模糊厌恶水平
此时惩罚项完全消失, 这样由Girsanov定理得出的(2.12)式和(2.13) 式中的漂移项系数
经过简单计算, 得到
除非需要强调
第二个不等式
3.1 验证定理
回到一般情形,
现在给出下面的验证定理.
定理3.1 (验证定理) 假设
则在区间
证 见附录B.
3.2 模糊厌恶下的最小Drawdown概率
本节我们分别求在
当
当
观察(3.2) 和(3.3) 式, 发现两式有相同的HJB方程, 而边界值条件不同. 注意花括号内表达式中,
引理3.1
证 引理证明同文献[9], 此处省略.
由上述引理, 根据二阶条件找到最优策略
从而
由引理3.1可知
其中
对于上述方程, 当
注3.1 没有模型参数的进一步限制, Isaaca条件不能满足我们的稳健问题. 假设
作线性变换
从而得到
最优鲁棒投资策略和最优鲁棒再保险策略分别为
令
则有
因此, 如果
作线性变换
从而得到
综合上述分析结果, 我们首先给出模糊厌恶下的最小drawdown概率, 以及相应的最优鲁棒投资策略和最优再保险策略.
定理3.2 设
其中
如果
对
模糊厌恶下的最优鲁棒投资策略和最优鲁棒再保险策略为
最优扭曲漂移分别为
其中, 我们记
证 (1)首先对
首先猜解
其中
经过计算得到
最后, 根据
(2) 接下来对
我们给出
首先猜解
其中
经过计算得到
最后, 根据
注3.2 我们给出特殊情形下的最优鲁棒值函数.
当
当
注3.3 验证Novikov条件. 结合(2.10), (2.11) 式和(3.5), (3.6) 式有
不等式成立是由于
4 规律和性质
本小节我们将要说明反馈形式的一些性质, 观察(3.12), (3.14)和(3.20) 式不难发现,
定理4.1 由(3.20) 式的
证 根据(3.2)式的HJB方程, 设
所以
并且
所以有
注4.1 因为
命题4.1
(1) 当
当
当
(2) 如果
证 当
令
将
则(4.1) 式表示在任何情况下, 无论
假设
观察(4.1)式, 我们发现如果
我们还注意到, 由于
接下来我们确定
(1)
情况1 当
并且
情况2 当
并且
情况3 当
并且
(2)
情况1 如果
情况2 如果
注4.2 根据反馈形式(3.7), 当
5 数值分析
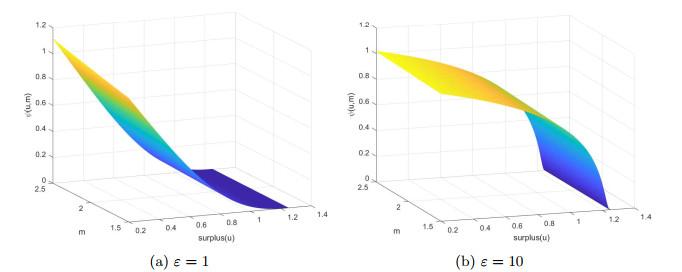
我们已经解决了边界值问题(3.2)-(3.3) 使用模型参数
图 1
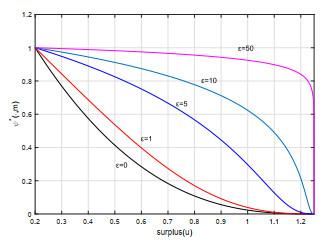
图 2
为分析不同模糊厌恶规避参数对值函数以及各个控制的具体影响, 我们在上述模型参数的基础上考虑
5.1 模糊厌恶水平对鲁棒最小drawdown概率的影响
观察图 2, 我们看到鲁棒最优值函数关于
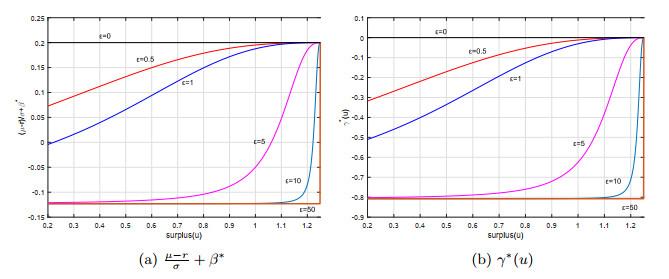
图 3
我们发现任何模糊厌恶水平下的最小drawdown概率都是关于
5.2 模糊厌恶水平对最优漂移扭曲的影响
我们知道最优扭曲漂移
最优扭曲漂移
观察两个最优扭曲漂移
6 结论与展望
本文中, 我们假设保险公司购买比例再保险并且将盈余投资与风险资产和无风险资产, 得出模糊厌恶框架下的最小drawdown概率和相应的鲁棒最优投资和再保险策略. 模糊厌恶在本文中具体表现为金融市场和保险市场的模型不确定性, 通过动态规划原理, 求出了鲁棒最优策略和值函数的解析解.
本文的创新点和结论主要体现在以下几个方面. 首先从最小drawdown概率的角度来研究模糊厌恶下保险公司的最优决策问题. 目前关于模型不确定性的研究大部分以效用函数为研究角度, 我们从风险控制理论出发, 联系保险公司实际运营情况, 研究模型不确定下保险公司的最小drawdown概率问题. 利用线性变化, 巧妙地对值函数进行求解. 通过与确定模型下最小drawdown问题的最优结果对比以及数值分析, 我们知道对于保险公司是否应该关心模糊厌恶, 就投资和再保险问题而言, 这并不是有用的信息, 因为是否考虑模糊厌恶对投资和再保险策略并不会产生影响. 但是通过观察不同模糊厌恶规避参数对最小drawdown概率的影响, 可以得出模糊厌恶对值函数影响较大, 也就是说保险公司做出的投资和再保险决策使保险公司承担的风险大大增加, 因此保险公司应该关心较大
本文主要是在基础模型框架下对模糊厌恶的最小drawdown概率, 最优投资和再保险策略方面进行的研究, 所以本文所求的最优决策都是理想模型下的稳健最优决策. 接下来我们可以对复杂模型下的鲁棒最优问题进行研究. 比如, 我们可以研究金融市场与保险市场相关下的稳健投资策略; 另外, 我们考虑将投资于风险资产的资金加以约束或者考虑借贷下的稳健最优投资决策; 而且本文运用期望值保费原则收取保费, 我们可以在更广义的方差保费原则下对最优鲁棒再保险决策进行研究.
A 辅助函数
函数
和
B 定理3.1证明
证 本验证定理我们分3步完成.
步骤1 设
设
对
上述It
根据验证定理条件(2), (4) 有
所以有
等价于
根据条件(5), 一旦财富过程超过安全水平
步骤2 设
定义
根据It
与步骤1类似, It
其中It
所以有
令
因为
先假设
所以有
步骤3 设
其中
参考文献
Optimal investment policies for a firm with a random risk process: exponential utility and minimizing the probability of ruin
DOI:10.1287/moor.20.4.937 [本文引用: 1]
Optimal proportional reinsurance and investment with multiple risky assets and no-shorting constraint
DOI:10.1016/j.insmatheco.2007.11.002
Optimal investment and proportional reinsurance with constrained control variables
DOI:10.1002/oca.965
指数保费准则下的最优投资和比例再保险
Optiaml investment and proportional reinsurance under exponential premium calculation
Robust portfolio rules and asset pricing
DOI:10.1093/rfs/hhh003 [本文引用: 1]
CEV模型下鲁棒最优投资和超额损失再保险问题研究
Research on robust optimal investment and excess-of-loss reinsurance under CEV model
Optimal investment and premium control for insurers with ambiguity
DOI:10.1080/03610926.2019.1568487 [本文引用: 1]
Minimizing the probability of lifetime ruin under ambiguity aversion
DOI:10.1137/140955999 [本文引用: 2]
Optimal proportional reinsurance policies in a dynamic setting
DOI:10.1080/034612301750077338 [本文引用: 1]
Optimal investmet strategy to minimize the probability of lifetime ruin
Minimizing the probability of ruin when claims follow Brownian motion with drift
DOI:10.1080/10920277.2005.10596214 [本文引用: 1]
Optimal investment to minimize the probability of drawdown
DOI:10.1080/17442508.2016.1155590 [本文引用: 2]
Optimal proportional reinsurance to minimize the probability of drawdown under thinning-dependence structure
Minimizing the probability of lifetime drawdown under constant consumption
DOI:10.1016/j.insmatheco.2016.05.007 [本文引用: 1]
Optimal reinsurance and investment in danger-region and safe-region
DOI:10.1002/oca.2568 [本文引用: 3]