1 引言
变点检测问题起源于质量工程, 最初由[1]在研究质量检测过程中提出. 在连续抽样检测过程中, 由于生产过程中某一时刻发生故障, 导致产品的质量超过其质量控制范围, 故障发生的时刻就认为是变点. 简单概括, 变点就是时间序列模型中的某个或某些量发生变化的点. 变点分析, 就是利用一定的统计指标、统计方法或其他方法, 对时间序列进行识别分析, 判断这种变化是否显著, 并估计出变点的位置以及变化的幅度.
回归模型是用来描述因变量与自变量之间关系的数学模型. 通常认为, 回归模型的回归系数在整个样本空间是保持不变的. 但事实并非如此, 目前由于实际应用中数据的复杂性, 导致单一的回归模型已经不能很好的反映两者之间的关系, 因此分段回归模型引起了学者的广泛研究. Quandt[15]最先提出分段线性回归模型的概念. 之后此类模型的变点检测问题取得了很多研究成果, 其中被广泛应用的方法是极大似然法[16-18], 通过构造似然比统计量对分段线性回归模型的是否存在变点进行假设检验, 从而估计出变点的位置. 其次, 最小二乘法[19-20]和Bayes理论也被广泛使用. Tang等[21]运用Bayes理论研究了只有一个变点的分段线性回归模型, 得到了变点的后验分布、回归系数和共同方差的估计值. 对于非线性回归模型的变点问题, 由于非线性的估计困难, 在该方面的文献并不丰富. 其中Ciuperca[22]针对非线性回归模型中的多变点问题, 拓展了分段线性回归模型中的M -估计的结果, 得到了变点位置的渐进分布. 之后Ciuperca[23]考虑了非线性回归模型中的最小绝对偏差估计量, 得到了变点估计值的收敛速度和渐进分布, 并且当模型的误差包含离群值时, LAD方法具有更高的鲁棒性. Boldea和Hall[24]基于最小二乘原理, 给出了非线性回归模型中多变点的估计值.
变点问题是许多其它学科经常遇到的问题, 如动态优化问题中对动态环境的检测是设计高效动态优化算法设计的前提、信号处理中怎样探测与分离弱信号等等. 因此怎样准确有效的处理变点问题, 尤其是回归模型参数的变化问题, 具有理论意义与实践价值. 本文针对二分段回归模型, 研究因参数变化引起的模型结构发生改变的变点位置. 由于参数的变化导致数据来源于同类模型但非同一模型, 变点前后的两个子序列分别适应不同的回归模型. 目前研究这种分段回归模型参数变点的方法有极大似然法、最小二乘法、Bayes理论等, 但这些方法中能够检测到参数弱变化的较少. 本文利用文献[25]中数据流的非平稳性度量指标(NS), 构造针对回归模型参数变化的变点检测方法. 其原理是利用抽样数据流进行参数估计后所得残差序列的平稳性大小, 反映抽样数据流中是否存在变点. 如果NS值越大, 平稳性越低, 存在变点的可能性越大. 该方法通过选定合适的窗口大小并移动窗口, 比较不同窗口内残差序列的NS值, 最终找到参数发生变化的具体位置. 实验表明, 此方法能有效检测到二分段回归模型的变点位置. 对比实验发现, 在参数弱变化情况下的变点检测, 本文所提出的检测方法准确性更高.
2 预备知识
本节介绍非平稳性度量指标(NS)以及二分段回归模型变点问题的数学描述.
2.1 非平稳性度量指标NS
非平稳性度量的一个直接应用就是模型选择. 残差序列的平稳性反映模型的正确性与参数估计方法的优良性, 只有当残差序列足够平稳时, 模型才可能有较好的拟合优度. 如果残差序列不够平稳, 可以认为残差序列中还存在着某种趋势信号, 所选择的模型未达到最佳刻画系统效果. 实际上, 为了检验模型是否适合所给的数据, 只需要研究残差序列的非平稳性程度. 残差序列NS值的大小刻画了序列接近于i.i.d. 的程度, NS值越小, 序列越接近于i.i.d., 无模型选择错误.
2.2 二分段模型变点检测问题的数学描述
二分段回归模型变点检测问题可用数学语言描述如下.
设在时间区间
其中
3 变点检测方法的一般步骤
本文所构造的变点检测方法主要步骤可以描述为: 先确定一个最佳的滑动窗口长度, 然后通过滑动窗口确定变点存在的可能窗口, 最后在变点所在窗口内对变点的准确位置进行探测. 本节将详细介绍算法的几个关键步骤.
3.1 最优滑动窗口长度的定义
(1) 任意固定
(2) 对此
(3) 计算残差序列{
(4) 设置
则满足
(5) 重复实验
3.2 变点准确位置的探测
3.2.1 确定变点存在的可能窗口
(1) 根据选定的最优滑动窗口长度
(2) 计算残差序列
(3) 若
3.2.2 对变点的准确位置进行探测
对确实存在变点的窗口进行变点准确位置探测, 设变点存在于第
(1) 若
(2) 若
(3) 若
4 方法具体实施与结果分析
本节构造一系列二分段变点模型, 利用抽样数据来检验本文方法的有效性.
4.1 确定最优的滑动窗口长度
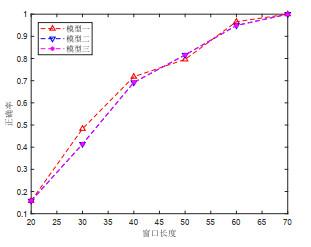
实验1 本实验以分段线性回归模型为例, 为了使变点在窗口的任何位置时都能被检测到, 以保证判断变点存在的可能窗口时, 不会出现错判、漏判等现象, 所以按照3.1中的实验步骤, 通过比较不同窗口长度下, 计算变点变化在不同位置时的非平稳性度量值, 根据判断变点存在的正确率是否大于阈值
取三组不同的参数构造三个不同的分段线性模型, 模型一:
对三个分段线性模型分别进行样本规模为
图 1
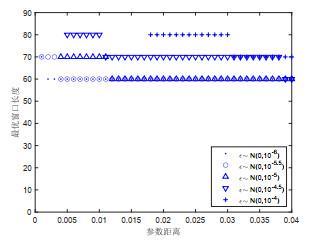
图 2
从实验结果可以看出
(1) 上述三个模型的最优窗口长度为
(2) 由图 2可知, 随着窗口长度的增大, 非平稳性度量指标NS对变点的检测能力也显著提高.
实验2 由于实验一获得的最优滑动窗口长度依赖于参数给定下的具体模型, 但在实际实验操作中, 事先是不知道相关参数的, 为了得到一般二分段线性模型的最优滑动窗口值, 设计180组二分段线性模型, 求得它们各自的最优滑动窗口长度, 从而给出了一般二分段线性模型最优滑动窗口的参考区间.
给定阈值0.04, 设置参数间的距离为
实验结果
从实验结果可以看出
(1) 图 3给出了180组分段线性模型的最优滑动窗口长度的分布值, 从图中可以看到模型的最优窗口的值分布在区间
图 3
(2) 对二分段线性变点模型, 无论参数之间差异有多大, 对应的最优窗口大小值基本在60左右. 在实际问题中, 虽不知模型参数具体的取值, 则可以把最优窗口值定为60.
4.2 方法的有效性
实验3 为了证明该方法的有效性, 设置变点处在线性回归模型、多元线性回归模型和非线性回归模型三类模型的不同位置, 分别构造如下分段模型, 按照3.2中的实验步骤, 进行模拟实验, 通过准确检测到变点位置的正确率来反映方法的有效性.
分别取三组不同的参数构造三个不同的分段线性模型, 模型一:
分别取三组不同的参数构造三个不同的分段多元线性模型, 模型四:
分别取三组不同的参数构造三个不同的分段指数模型, 模型七:
对三类分段模型分别进行样本规模为
设置变点位置
表 1.1 一元线性模型不同变点位置的检验能力
| 变点位置l1+1 | 无变点 | 11 | 41 | 101 | 161 | 191 |
| 模型一 | 100 | 95.5 | 96 | 98 | 99 | 99 |
| 模型二 | 100 | 96.5 | 97 | 99 | 98 | 99 |
| 模型三 | 100 | 95.5 | 97 | 97.5 | 97.5 | 99 |
表 1.2 多元线性模型不同变点位置的检验能力
| 变点位置l1+1 | 无变点 | 11 | 41 | 101 | 161 | 191 |
| 模型四 | 100 | 94.5 | 98.5 | 96.5 | 98.5 | 99 |
| 模型五 | 100 | 95 | 94.5 | 95.5 | 99.5 | 99 |
| 模型六 | 100 | 94.5 | 97.5 | 98 | 97 | 98.5 |
表 1.3 非线性模型不同变点位置的检验能力
| 变点位置l1+1 | 无变点 | 11 | 41 | 101 | 161 | 191 |
| 模型七 | 100 | 90 | 93 | 95.5 | 96 | 95.5 |
| 模型八 | 100 | 96 | 92 | 94 | 96.5 | 96.5 |
| 模型九 | 100 | 92.5 | 94 | 92 | 95.5 | 98 |
4.3 基于准确率的参数变化距离对噪声方差的敏感性分析
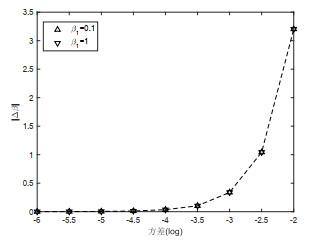
实验4 本实验以分段线性回归模型为例, 由于本文主要研究的是参数的弱变化导致的模型结构变点, 为了研究在怎样弱的参数变化里, 本文所用的方法均可以检测到变点位置, 所以在保证判断变点准确位置的正确率均高于95% 的前提下, 给出了噪声方差和可调节的最短的参数距离之间的关系. 其中
对模型(4.1)取参数
对分段线性模型分别进行样本规模为
设置变点位置为
图 4
5 与其它方法的比较
对模型(4.1)、(4.2)和(4.3)分别取三组不同的参数构造三类不同的分段模型.
一元线性模型: 模型一:
二元线性模型: 模型一:
非线性模型: 模型一:
对三类分段模型分别进行样本规模为
设置变点位置
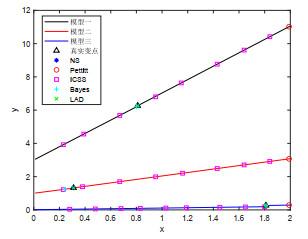
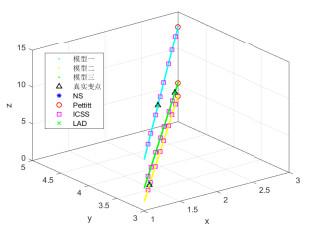
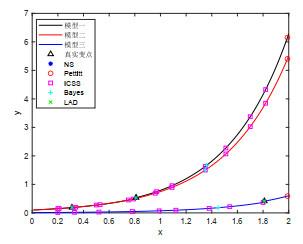
图 (5a)
图 (5b)
图 (5c)
由图 5(a)、图 5(b)、图 5(c)可知, 本文方法能准确检测到三类分段模型中变点的位置, Pettitt法检测到的变点与真实变点之间存在较大的误差, 而Mann-Kendall法未检测到变点, ICCS(迭代累积平方和算法)则存在严重的变点数目高估问题, 将一些本不是变点的点作为变点, Bayes方法对于分段一元线性模型中处于序列尾部的变点可以准确检测到, 但对于序列中部和前部的变点位置, 估计存在偏差, 并且对于分段多元线性模型和非线性模型的变点位置估计均不准确, LAD法虽然也能够准确检测到三类分段模型中变点的位置, 但根据表 2可以看出LAD方法所耗费的时间成本远高于本文提出的方法, 通过上述典型算法对三类模型变点位置的估计情况, 明确了该方法的优良性和准确性.
表 2 运行时间比较(s)
| 方法 | LAD | NS | ||||
| 变点位置 | 31 | 81 | 181 | 31 | 81 | 181 |
| 一元线性 | 79.256 | 77.196 | 77.890 | 1.178 | 0.702 | 0.970 |
| 多元线性 | 74.172 | 76.543 | 74.306 | 0.684 | 0.489 | 1.015 |
| 非线性 | 133.999 | 111.789 | 141.534 | 23.933 | 16.690 | 19.350 |
6 总结与展望
时间序列作为一种典型的数据类别, 已广泛存在于各种实际应用场景中. 其中, 变点检测作为时间序列数据分析的重要研究方向之一, 在经济、气象、水文等实际应用中发挥着重要作用. 然而在目前针对回归模型变点检测方法的研究上, 还存在着对模型依赖性强、准确率不高、计算迭代时间成本高等不足. 本文基于非平稳性度量指标(NS), 利用抽样数据流进行参数估计后所得残差序列的平稳性大小, 反映了抽样数据流中是否存在变点, 通过选定合适的窗口大小并移动窗口, 比较不同窗口内数据流的NS值判断变点的精确位置, 以此构造了针对回归模型参数变化的变点检测方法, 该方法完全不需要知道序列的分布信息, 模型依赖性较弱, 比较实验的结果也表明了该方法在线性回归模型和非线性回归模型中都具有较高的准确率, 并且时间成本远低于其他方法. 在模拟实验过程中当自变量出现重叠区间的情况时, 该方法的检测效果会下降, 将在后续的工作中继续探讨更能处理此种情形的方法, 并且希望能够把该方法推广到自回归模型或其它模型的变点检测问题中.
参考文献
Continuous inspection schemes
Use of cumulative sums of squares for retrospective detection of changes of variance
Annual and seasonal climatic variations over the northern hemisphere and Europe during the last century
A nonparametric approach to the change-point problem
跳-斜度变点估计的强收敛速度
DOI:10.3969/j.issn.0253-2778.2011.09.004 [本文引用: 1]
The strong convergence rate of jump-slope change point estimation
DOI:10.3969/j.issn.0253-2778.2011.09.004 [本文引用: 1]
关于分布变点问题的非参数统计推断
Nonparametric statistical inference on the distribution change point
On score vector-and residual-based CUSUM tests in ARMA-GARCH models
基于分位点回归模型变点检测的金融传染分析
DOI:10.3969/j.issn.1000-3894.2007.10.015 [本文引用: 1]
Analysis of financial contagion based on change point detection of quantile regression model
DOI:10.3969/j.issn.1000-3894.2007.10.015 [本文引用: 1]
基于Copula变点检测的美国次级债金融危机传染分析
DOI:10.3321/j.issn:1003-207X.2009.03.001
Analysis of the contagion of U.S. subprime debt financial crisis based on copula change coint detection
DOI:10.3321/j.issn:1003-207X.2009.03.001
A change point approach for the identification of financial extreme regimes
Bayesian change-point analysis in hydrometeorological time series. Part 1:The normal model revisited
DOI:10.1016/S0022-1694(00)00270-5 [本文引用: 1]
Bayesian change point analysis for extreme daily precipitation
DOI:10.1002/joc.4904 [本文引用: 1]
Cancer outlier detection based on likelihood ratio test
DOI:10.1093/bioinformatics/btn372 [本文引用: 1]
Mapping the order and pattern of brain structural MRI changes using change-point analysis in premanifest Huntington's disease
DOI:10.1002/hbm.23713 [本文引用: 1]
The estimation of the parameters of a linear regression system obeying two separate regimes
DOI:10.1080/01621459.1958.10501484 [本文引用: 1]
Tests of the hypothesis that a linear regression system obeys two separate regimes
DOI:10.1080/01621459.1960.10482067 [本文引用: 1]
Changepoint estimation in a segmented linear regression via empirical likelihood
Testing for threshold effects in regression models
DOI:10.1198/jasa.2011.tm09800 [本文引用: 1]
Estimation of a change point in multiple regression models
DOI:10.1162/003465397557132 [本文引用: 1]
门槛回归模型中门槛值和回归参数的估计
Estimation of threshold and regression parameters in threshold regression model
Bayesian analysis for change-point linear regression models
The M-estimation in a multi-phase random nonlinear model
Estimating nonlinear regression with and without change-points by the LAD method
Estimation and inference in unstable nonlinear least squares models
基于非平稳性度量的彩票数据实证分析
Empirical analysis of lottery data based on non-stationarity measure