1 引言
数字印章技术[1]以数字技术模拟传统实物印章, 其管理、使用方式符合实物印章的习惯和体验. 数字印章的具体做法是将电子文书内容的数字签名通过数字水印、加密等技术, 使其和数字印章图像进行有效的绑定. 验证数字印章真伪的过程其实就是验证数字签名的过程, 通过数字签名以及验证技术证明与数字印章相关联的电子文书是真实的, 数字印章图像才被承认是有效的. 数字印章所基于的数字签名匹配技术是信息与数据安全的核心技术之一, 可以实现身份认证、数据完整性保护、防篡改、防冒充以及不可否认性等数据传输中的需求. 随着大数据时代的到来, 数字印章技术将会在消息鉴别机制中发挥重要的作用.
数字印章基于的数字签名技术, 不关注算法的保密性, 即算法公开, 它的数据安全与密钥的保密程度有很大的关系. 所涉及的加密技术分为对称加密和非对称加密. 常见的对称加密算法有: AES(Advanced Encryption Standard)[2], IDEA(International Data Encryption Algorithm)[3]等. 对称加密具算法公开、计算量小、加密速度快、加密效率高的优点. 但每对用户每次使用对称加密算法时, 都需要使用其他人不知道的独一密钥, 这会使得收、发双方所拥有的钥匙数量巨大, 密钥管理成为双方的负担. 随着Diffie和Hellman提出公钥密码思想后[4], 已产生了基于离散对数的签名, 基于椭圆曲线的签名[5]等非对称加密技术, 在保护通信安全方面,非对称加密算法具有对称密码难以企及的优势. 但非对称加密算法比对称加密算法慢数千倍. 两种加密技术各有优劣, 我们尝试从一个新的视角来对信息进行加密并设计数字印章.
在实际生活和工作中, 人们通常通过云计算的方式来充分利用各部门的计算资源和数据资源, 这对信息安全带来了巨大的隐患. 例如政府签发文件盖章, 由于签发文件数量多, 容易出现泄密, 以及对印章进行仿造和对文件进行篡改. 出于版权保护、国家安全、犯罪追查等因素的考虑, 常常需要对数字印章信息进行保密匹配, 即把印章信息加密后进行自动匹配认证(不让操作人员看到印章信息的真实内容). 所谓的数字印章的保密匹配就是研究经过加密后的数字印章与印章信息匹配认证问题, 使用这一匹配技术的普通用户, 无法通过自身人眼或其它方法在匹配数字印章的输入和匹配结果的输出过程中辨识出图片上所展示的数据信息, 从而满足特殊场合下的保密需求. 现有的加密方法目标是为了信息在传输过程中的安全, 存在基于密钥的解密的算法, 从而保证信息在传输过程中的安全和解密后的信息质量. 由于解密算法的存在, 总存在泄密的可能(密钥丢失, 被非法窃取等). 本文提出的数字印章加密技术与现有的加密技术最大的区别是: 只加密, 不解密, 加密只是起掩盖目标信息的作用.
我们设计的数字印章采用服从独立均匀分布的噪声序列对原始数据信息进行掩盖. 从图像保密匹配的角度看, 它实际上是一种图像掩盖方法. 主要在图像数据中加入很强的随机噪声, 使图像难以辨认. 由于噪声强度远大于信号强度从而能够达到对于原始数据安全加密的目的. 现有的加密方法旨在传递信息, 必定对应于一个快速的依赖于密钥解密算法. 而本文中由于服从同分布的噪声序列是随机的, 对于一个原始数据信息可以产生不同的噪声序列进行加密, 生成数字印章都彼此不同. 采用的实际上是"一次一密"的加密算法思想, 加密旨在掩盖图像信息, 不需要解密. 当进行身份认证时, 仅需要根据这一原始数据信息就可以完成. 解决了传统对称加密算法中管理密钥这一问题, 使用了"一次一密"的优点, 使得破解难以一劳永逸. 相较非对称加密技术, 该数字印章技术用户操作步骤少, 减少了使用双方操作成本.
本文简要介绍时间序列的非平稳性度量的定义及近似计算方法, 将其应用到数字印章设计和匹配. 利用残差序列非平稳性度量值, 对真伪信息进行身份判别, 并通过理论和仿真实验给出判别准确率结果. 我们所设计的数据印章包含了时间信息、设备信息、文件内容信息以及自定义信息, 全面的涵盖了加盖数字印章的时空属性, 并与加盖载体具有关联性. 匹配结果能够有效准确的对真伪信息进行判别, 且准确率高, 鲁棒性好.
2 稳定集合与稳定信息结构
2.1 稳定集合的定义与判别
设
其中
在有限样本下, 基于概率论中大数定律和中心极限定理, 可以采用如下稳定集合判别标准: 对于序列样本
以及
当
同统计学的假设检验一样, 有限频率序列的收敛准则
2.2 稳定信息结构(SIS: Stable Information Structure)
对于有限长数据流样本, 在稳定集合判别准则
1) 输入序列
2) 选择初始划分方式(一般取等长均匀区间)将相应空间划分为
3) 以分割点
4) 若
5) 若
6) 由稳定区间集合生成稳定信息结构
与此同时, 还可以考虑一种从右到左稳定区间搜索算法, 即从最右端节点
3 非平稳性度量指标
有了稳定集合的定义、有限样本下稳定集合判别标准
其中,
时间序列的非平稳性度量定义为
其中,
对
其中
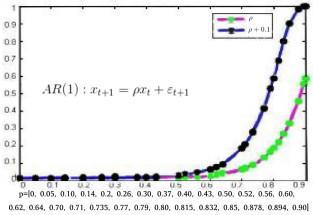
从图 1可以看出,
图 1
上述结论验证NS值是时间序列非平稳程度的一个良好刻画. 时间序列越平稳, 在给定的稳定标准和初始划分下, 得到的稳定集合越多, 稳定信息结构越精细, 从而NS值也就越小. 对于独立同分布数据, 其NS值为0或接近于0; 对于趋势性较强的数据, 其NS值为1或接近于1.
我们将利用此实验结果设计数字印章, 本文在置信水平
4 数字印章生成
数字印章用以生成唯一确定的信息, 即包含加盖印章时间信息、加盖印章所用设备信息、与所加盖文章内容关联信息以及加盖用户自定义信息. 对在不同时间、设备、载体等数字媒介上进行盗用、篡改行为起到防护识别的目的.
数字印章包含两部分: 信息序列与噪声序列. 数字印章对目标信息构造信息序列, 并用以之后的匹配认证. 噪声序列一方面对信息序列加以掩盖起到加密作用, 另一方面平稳的噪声序列对数字印章的匹配, 并通过计算残差序列的NS值来判别信息真伪提供了度量标准.
4.1 构造信息序列
信息序列应满足以下三个性质:
1) 固定信息所生成的信息序列也是固定且唯一的;
2) 信息序列对于信息是敏感的, 换而言之, 相似的信息所构造出的信息序列显著不同;
3) 信息序列与图片可互相转换, 即信息序列值为正整数且取值范围在[0, 255]以内.
当信息发生微小变动或存在相似伪信息时, 所构造的信息序列应与原信息所构造的信息序列呈显著差异. 这一差异会为原本平稳的噪声序列带来冗余趋势, 使得噪声序列非平稳, 即
其中
由于非平稳性度量指标NS的准确度依赖序列的长短, 即序列越长度量越准确, 相应计算量越大. 这里我们选择以合适的长度256来构造信息序列
1) 原始信息为Inf, 对原始信息进行Hash加密映射. 这里采用MD5算法得到32位字母与数字组合的有序序列Hinf = hash(Inf);
2) 将哈希有序序列Hinf转化为ASCII编码, 得到有序序列Ainf = ASCII(Hinf). 对序列Ainf进行展开得到取值在[0, 9]的有序序列. 例: Ainf为
3) 按照序列各项值重复进行展开得到序列
4) 对3) 步骤中得到的序列每一项乘以9得到序列Minf;
5) 将序列Minf重复排列, 截断为长度为256的最终信息序列X.
上述步骤1)–3)使得相似信息所构造的序列差异尽可能大, 步骤4)使序列对于加盖噪声后所得到的序列对信息的变动敏感. 构造步骤所生成的信息序列满足信息序列所应满足的性质.
4.2 构造噪声序列
噪声序列对信息序列加以掩盖, 起到对于信息加密的目的. 由于生成独立同分布的噪声具有随机性, 使得不同数字印章具有不同的噪声序列, 使得破解方法难以一劳永逸.
由于不同随机数生成器生成服从独立同分布的噪声方式不同. 那么有必要通过一种统一计算NS的方式来对生成的噪声进行约束, 其判别标准与提取算法在第三章中进行了说明. 构造平稳的噪声序列换而言之, 是对于固定长度N的序列, 产生服从独立同分布的噪声序列, 使其计算得到的NS值为0. 构造噪声序列
4.3 数字印章设计
数字印章包含四部分内容, 下面分别进行阐述
1) 时间信息: 时间信息具有时效性. 对于同一数字内容, 不通的加盖时间能够有效的防止批量复制加盖;
2) 设备信息: 加盖印章所用设备为用户进行操作地点的重要依据, 对于某些具有授权的设备具有特定的权限, 不同设备也具备不同的机器指纹. 也是印章信息存储的重要载体. 获取设备信息的唯一性使这一信息匹配成为判别信息真伪的有效依据;
3) 内容信息: 内容信息包含加盖文件载体的标题、签署人、机构(单位)等. 该信息使数字印章与加盖载体相关联, 从而达到"一章一版"的效果;
4) 自定义信息: 自定义信息在信息匹配中有独特的作用. 在同一时间、同一设备以及加盖相同文章的情况下, 可对分发印章分数进行编号. 当发生文件泄漏, 可以匹配自定义信息确定泄漏源头.
通过4.1节与4.2节的方法对上述数字印章四部分的内容分别构造长度为256的信息序列
图 2
图 3
图 4
图 5
5 数字印章匹配
数字印章的信息匹配本质上是对数字印章反向获取残差序列, 并计算残差序列NS值的过程. 对于给定的数字印章获取印章序列
4.3节中, 数字印章包含四部分内容. 针对不同内容进行四次独立信息匹配, 计算相应NS值, 记为
对于三通道彩色数字印章, 其匹配结果当且仅当每一通道NS值为0时, 判别原始信息为真. 如果每一通道的信号是独立的(做了Hash操作以后, 不同通道之间的关联被破坏了), 特定内容每一通道的匹配准确率记为
6 仿真结果
构造原始信息序列
1) 以时间信息"2020 01-01 12.12.12 Wen Jan"按照4.1节所述构造长度为256的信息序列
图 6
2) 对图 6数字印章图片进行信息匹配操作. 首先由数字印章图片反向获取印章序列
进一步实验结果见表 1.
表 1 实验仿真结果
| 数字印章内容 | 试验次数 | 匹配准确率(单通道) | 匹配准确率(三通道) |
| 单一信息(NSi) | 50 | 92% | 100% |
| 100 | 93% | 100% | |
| 500 | 93% | 100% | |
| 1000 | 93.2% | 100% | |
| 总信息(NSsum) | 50 | 100% | 100% |
| 100 | 100% | 100% | |
| 500 | 100% | 100% | |
| 1000 | 100% | 100% |
观察表 1, 其结果与第5节得到的理论值保持一致. 数字印章检验准确率高, 效果稳定, 对于辨别真伪信息的鲁棒效果好. 较之灰度图, 彩色数字印章可以更为有效对信息进行匹配.
7 总结
本文基于非平稳性度量并利用随机加密匹配方法设计了一种数字印章. 它包含了盖章时的时间和设备信息, 以及与盖章载体相关联的内容和自定义信息. 确保不同时间空间不同内容数字印章唯一且对内容变化敏感. 数字印章选择服从独立均匀分布的零均值噪声序列对原始数据信息进行加密, 这种加密方法主要是用噪声掩盖真实信息, 要破解只能采用去噪的方法, 由于噪声很强(信噪比通常小于-5), 传统的去噪方法得不到好的结果. 我们的加密方法是难以破解的, 可以防止量子计算方法的破解. 所采用的匹配算法基于残差序列的非平稳性度量的计算, 不需要进行解密, 克服了传统对称加密算法中对于大量密钥管理的问题. 仿真实验表明该方法能够精确实现匹配认证, 匹配准确率与理论值保持一致, 达到数字印章防篡改、防盗用的目的, 在版权保护, 身份认证等安全领域中有着广泛的应用.
参考文献
电子印章与传统印章的比较研究
A comparative study of electronic seal and the traditional seal
A highly efficient and secure hardware implementation of the advanced encryption standard
DOI:10.1016/j.jisa.2019.102371 [本文引用: 1]
An analysis of international data encryption algorithm(IDEA) security against differential cryptanalysis
New direction in cryptography
基于时间释放加密和数字签名的匿名电子投票方案
DOI:10.3969/j.issn.1000-386x.2016.12.076 [本文引用: 1]
Anonymous electronic voting scheme based on time-released encryption and digital signature
DOI:10.3969/j.issn.1000-386x.2016.12.076 [本文引用: 1]
数据流的非平稳性度量
Nonstationarity measure of data stream
基于非平稳度量的灌溉用水量预测模型选择
Selection of forecasting models for irrigation water consumption based on nonstationarity measure
基于非平稳性度量的彩票数据实证分析
Empirical analysis of lottery data based on non-stationarity measure
基于EMD及非平稳性度量的趋势噪声分解方法
DOI:10.3969/j.issn.1003-3998.2016.04.016 [本文引用: 1]
Decomposition of noise and trend based on EMD and non-stationarity measure
DOI:10.3969/j.issn.1003-3998.2016.04.016 [本文引用: 1]