共轭梯度法是求解大规模光滑无约束优化问题$ \min\{f(x)|\ x\in {{\Bbb R}} ^n\} $的最有效方法之一, 其迭代公式的一般形式为

(1.1) $ \begin{equation} x_{k+1} = x_k+\alpha_k d_k, \end{equation} $

(1.2) $ \begin{eqnarray} d_k = \left\{ \begin{array} {lll}-g_k, &k = 1, \\ -g_k+\beta_kd_{k-1}, &k\geq2, \end{array}\right. \end{eqnarray} $

其中$ g_k = \nabla f(x_k) $, $ \alpha_k $为搜索步长, $ d_k $为搜索方向, $ \beta_k $为方向调控参数. 步长通常可由标准Wolfe线搜索产生, 即$ \alpha_k $满足

(1.3) $ \begin{equation} \left\{\begin{array}{ll} f(x_k+\alpha_k d_k)\leq f(x_k)+\delta\alpha_k g_k^Td_k, \\ g(x_k+\alpha_k d_k)^T d_k\geq\sigma g_k^Td_k, \end{array}\right. \end{equation} $

或由强Wolfe线搜索获得

(1.4) $ \begin{equation} \left\{\begin{array}{ll} f(x_k+\alpha_k d_k)\leq f(x_k)+\delta\alpha_k g_k^Td_k, \\ |g(x_k+\alpha_k d_k)^T d_k|\leq\sigma |g_k^Td_k|, \end{array}\right. \end{equation} $

其中参数$ \delta $和$ \sigma $满足$ 0 < \delta < \sigma < 1 $. 不同的$ \beta_k $对应不同的共轭梯度法, 著名的$ \beta_k $计算公式有

$ \beta_k^{\rm HS} = \frac{{g_k^T}(g_k-g_{k-1})}{{d_{k-1}^T}(g_k-g_{k-1})}, \ \beta_k^{\rm FR} = \frac{\|g_k\|^2}{\|g_{k-1}\|^2}, \ \beta_k^{\rm PRP} = \frac{{g_k^T}(g_k-g_{k-1})}{\|g_{k-1}\|^2}, \ \beta_k^{\rm DY} = \frac{\|g_k\|^2}{{d_{k-1}^T}(g_k-g_{k-1})}, $

与上述四个公式相对应的共轭梯度法分别称为HS方法^[1]、FR方法^[2]、PRP方法^[3-4]和DY方法^[5], 其中FR方法和DY方法具有良好的收敛性质, HS方法和PRP方法的数值性能优良. 因此, 为寻求收敛性和数值效果都理想的方法, 基于上述调控参数所建立的共轭梯度法均被广泛研究^[6-14]. 为了确保PRP公式非负, 文献[6]提出了PRP公式的一种变形, 记为WYL参数公式

(1.5) $ \begin{eqnarray} \beta_k^{\rm WYL} = \frac{g_{k}^{T}(g_{k}-\frac{\|g_k\|}{\|g_{k-1}\|}g_{k-1})}{\|g_{k-1}\|^{2}}, \end{eqnarray} $

WYL方法不仅传承了PRP方法的性质, 而且文献[7]证明了在强Wolfe搜索条件下($ \sigma\in (0, \frac14) $)全局收敛. 借鉴WYL方法的思想, 文献[8]改进了HS共轭梯度法, 称之为YWH方法, 其共轭参数公式为

(1.6) $ \begin{eqnarray} \beta_k^{\rm YWH} = \frac{g_{k}^{T}(g_{k}-\frac{\|g_k\|}{\|g_{k-1}\|}g_{k-1})}{d_{k-1}^T(g_k-g_{k-1})}, \end{eqnarray} $

该方法在强Wolfe搜索条件下($ \sigma\in (0, \frac13) $)是全局收敛的. 为了扩大上述两方法的强Wolfe搜索中参数$ \sigma $的取值范围, 文献[9]对WYL公式和YWH公式进行了改进, 得到了两个新公式

(1.7) $ \begin{equation} \beta_k^{\rm NPRP} = \frac{\|g_{k}\|^{2}-\frac{\|g_k\|}{\|g_{k-1}\|}|g_{k}^{T}g_{k-1}|}{\|g_{k-1}\|^{2}}, \ \ \beta_k^{\rm NHS} = \frac{\|g_{k}\|^{2}-\frac{\|g_k\|}{\|g_{k-1}\|}|g_{k}^{T}g_{k-1}|}{d_{k-1}^T(g_k-g_{k-1})}, \end{equation} $

显然, $ 0\leq\beta_k^{\rm NPRP}\leq \beta_k^{\rm FR} $和$ 0\leq\beta_k^{\rm NHS}\leq \beta_k^{\rm DY} $, 并证明由新公式产生的算法不仅每步迭代都可获得充分下降的搜索方向, 且在强Wolfe线搜索条件及参数$ \sigma\in(0, \frac12) $下全局收敛. 最近, 结合强Wolfe线搜索(1.4)式的第二个不等式, 文献[13]给出了具有充分下降性的改进FR型和DY型共轭梯度法, 两个方法不仅保持了FR和DY方法的性能, 而且具有良好的收敛性质和数值效果, 其共轭参数公式分别为

(1.8) $ \begin{equation} \beta_k^{\rm IFR} = \frac{\|g_{k}\|^{2}}{\|g_{k-1}\|^{2}}\cdot\frac{|g_{k}^Td_{k-1}|}{-g_{k-1}^Td_{k-1}}, \ \ \beta_k^{\rm IDY} = \frac{\|g_{k}\|^{2}}{d_{k-1}^T(g_k-g_{k-1})}\cdot\frac{|g_{k}^Td_{k-1}|}{-g_{k-1}^Td_{k-1}}. \end{equation} $

该文借鉴文献[9, 13]的思想, 为获得强Wolfe线搜索中参数$ \sigma $更大的取值范围, 对(1.7)式中两个参数公式进一步修正, 并得到如下的两个改进公式

(1.9) $ \begin{eqnarray} \beta_k^{\rm IPRP} = \frac{\|g_{k}\|^{2}-\frac{\|g_k\|}{\|g_{k-1}\|}|g_{k}^{T}g_{k-1}|}{\|g_{k-1}\|^{2}} \frac{|g_{k}^T d_{k-1}|}{-g_{k-1}^T d_{k-1}}, \end{eqnarray} $

(1.10) $ \begin{eqnarray} \beta_k^{\rm IHS} = \frac{\|g_{k}\|^{2}-\frac{\|g_k\|}{\|g_{k-1}\|}|g_{k}^{T}g_{k-1}|}{d_{k-1}^T(g_k-g_{k-1})} \frac{|g_{k}^T d_{k-1}|}{-g_{k-1}^T d_{k-1}}, \end{eqnarray} $

显然, $ 0\leq\beta_k^{\rm IPRP}\leq \sigma\beta_k^{\rm FR} $和$ 0\leq\beta_k^{\rm IHS}\leq \sigma\beta_k^{\rm DY} $. 每一次迭代中, 由新公式所产生的两个共轭梯度法都可获得充分下降的搜索方向, 利用强Wolfe线搜索获得搜索步长, 并证明由公式$ \beta_k^{\rm IPRP} $和$ \beta_k^{\rm IHS} $所产生的改进方法分别在参数$ \sigma\in(0, \frac{\sqrt{2}}2) $和$ \sigma\in(0, 1) $下是全局收敛的. 最后, 对所提出的新方法进行数值测试, 并与其它同类方法进行比对, 数值结果表明该文所提出的两个方法是有效的.

基于公式(1.9)和(1.10), 建立该文算法框架如下.

初始化. 任取初始点$ {x_1}\in{{{\Bbb R}}^n} $, 给定精度$ \varepsilon > 0 $, 参数$ 0 < \delta < \sigma < 1 $, $ d_1 = -g_1, k = 1 $.

步骤1   若$ {\|g_k\|} < \varepsilon $, 则停止. 否则, 转入步骤2.

步骤2   由强Wolfe线搜索准则产生步长$ \alpha_k $, 即$ \alpha_k $满足不等式组(1.4).

步骤3   令$ {x_{k+1} = {x_k}+{\alpha_k}{d_k}} $, 计算梯度$ g_{k+1}: = g(x_{k+1}) $, 利用(1.9)或(1.10)式获得参数公式$ \beta_{k+1} $, 即$ \beta_{k+1}: = \beta_{k+1}^{\rm IPRP} $ 或$ \beta_{k+1}: = \beta_{k+1}^{\rm IHS} $.

步骤4   令$ d_{k+1} = -g_{k+1}+\beta_{k+1}d_k $. 置$ k: = k+1 $, 返回步骤1.

为便于分析, 记IPRP方法和IHS方法分别为由参数公式$ \beta_k^{\rm IPRP} $和$ \beta_k^{\rm IHS} $所产生的新算法.

为获得算法的收敛性, 首先给出算法所需的两个常规假设条件.

(H1) 函数$ f(x) $在水平集$ \Lambda = \{x\in R^n|f(x)\leqslant f(x_1)\} $上有下界, 其中$ x_1 $为算法初始点.

(H2) 函数$ f(x) $在水平集$ \Lambda $的某邻域$ U $内可微, 且其梯度函数$ g(x) = \nabla f(x) $满足Lipschitz条件, 即存在常数$ L > 0 $, 使$ \|g(x)-g(y)\|\leq L\|x-y\|, \forall\ x, y\in U $.

下面引理所给出的是著名Zoutendijk条件^[15], 其在共轭梯度法全局收敛性分析中起着非常重要的作用.

引理3.1   设假设(H1)和(H2)成立, 考虑一般迭代方法(1.1)–(1.2), 若搜索方向$ d_k $满足$ g_k^Td_k < 0 $, 步长因子$ \alpha_k $ 满足标准Wolfe线搜索准则, 则有$ \sum\limits_{k = 1}^\infty\frac{(g_k^Td_k)^2}{{\|d_k\|}^2} < \infty $成立.

对于无约束优化问题, 若存在常数$ c > 0 $, 使得迭代点列$ \{x_k\} $及相应的搜索方向序列$ \{d_{k}\} $满足

(3.1) $ \begin{equation} g_k^Td_k\leq -c\|g_{k}\|^{2}, \ \ \forall\ k, \end{equation} $

称搜索方向$ d_k $满足充分下降条件.

接下来, 将分析IPRP算法的全局收敛性. 为此, 首先证明IPRP算法所产生的搜索方向在强Wolfe线搜索准则下均为充分下降的.

引理3.2  设假设(H2)成立, 且方向$ d_{k} $由IPRP共轭梯度法产生. 若参数$ \sigma $满足$ 0 < \sigma < \frac{\sqrt{2}}{2} $, 则对所有的$ \forall\ k\geq 1 $, 总有下式成立

(3.2) $ \begin{eqnarray} -\frac{1}{1-\sigma^{2}} \leq \frac{g_k^Td_k}{\|g_{k}\|^2}\leq-\frac{1-2\sigma^{2}}{1-\sigma^{2}}. \end{eqnarray} $

证  当$ k = 1 $时, 有$ g_1^Td_1 = -\|g_1\|^2 $, 结论显然成立. 假设结论(3.2)对$ k-1 $($ k\geq2) $成立. 下面证明其对$ k $也成立. 记梯度向量$ g_k $和$ g_{k-1} $之间的夹角为$ \theta_k $, 易知

(3.3) $ \begin{equation} \|g_{k}\|^{2}-\frac{\|g_k\|}{\|g_{k-1}\|}|g_{k}^{T}g_{k-1}| = \|g_k\|^2-\|g_k\|^2|\cos\theta_{k}| = \|g_k\|^2(1-|\cos\theta_{k}|). \end{equation} $

利用(1.2)和(1.9)式, 立得

(3.4) $ \begin{eqnarray} \frac{g_{k}^Td_{k}}{\|g_{k}\|^2} & = &-1+\frac{\|g_{k}\|^{2}-\frac{\|g_k\|}{\|g_{k-1}\|}|g_{k}^{T}g_{k-1}|}{\|g_{k-1}\|^{2}} \frac{|g_{k}^T d_{k-1}|}{-g_{k-1}^T d_{k-1}}\frac{g_k^Td_{k-1}}{\|g_{k}\|^2}{}\\ & = &-1+\frac{\|g_k\|^2(1-|\cos\theta_{k}|)}{\|g_{k-1}\|^2}\frac{|g_{k}^T d_{k-1}|}{-g_{k-1}^T d_{k-1}}\frac{g_k^Td_{k-1}}{\|g_{k}\|^2}. \end{eqnarray} $

考虑到强Wolfe线搜索(1.4)的第二个不等式和归纳假设, 有

(3.5) $ \begin{equation} |g^T_kd_{k-1}|\leq \sigma |g_{k-1}^Td_{k-1}| = -\sigma g_{k-1}^Td_{k-1}, \ \hbox{ 或}\ \frac{|g^T_kd_{k-1}|}{-g_{k-1}^Td_{k-1}}\leq \sigma. \end{equation} $

将(3.5)式代入(3.4)式, 可得

(3.6) $ \begin{equation} -1+\sigma^2 \frac{g_{k-1}^Td_{k-1}}{\|g_{k-1}\|^2}\leq-1-\sigma\frac{|g_k^Td_{k-1}|}{\|g_{k-1}\|^2}\leq \frac{g_k^Td_{k}}{\|g_{k}\|^2} \leq -1+\sigma\frac{|g_k^Td_{k-1}|}{\|g_{k-1}\|^2}\leq -1-\sigma^2\frac{g_{k-1}^Td_{k-1}}{\|g_{k-1}\|^2}. \end{equation} $

进而, 对(3.6)式利用$ k-1 $的归纳假设, 不难得到

$ \begin{eqnarray*} -\frac{1}{1-\sigma^2} = -1+\sigma^{2}(-\frac1{1-\sigma^{2}})\leq \frac{g_k^Td_{k}}{\|g_{k}\|^2}\leq -1-\sigma^{2}(-\frac1{1-\sigma^{2}}) = -\frac{1-2\sigma^{2}}{1-\sigma^{2}}. \end{eqnarray*} $

因此, 关系式(3.2)对所有的$ k\geq1 $都成立. 证毕.

由引理3.2可知, 当$ 0 < \sigma < \frac{\sqrt{2}}{2} $时, 记$ c\triangleq\frac{1-2\sigma^{2}}{1-\sigma^{2}} $, 由IPRP方法所产生的方向均满足充分下降条件(3.1). 下面证明IPRP方法满足Glibert和Nocedal在文献[14]中所给出的性质$ (\ast) $.

引理3.3  设假设(H1)和(H2)成立, 对任意的$ k\geq1 $, 若满足$ 0 < \gamma\leq\|g_{k}\|\leq\bar{\gamma} $, 则IPRP方法在强Wolfe线搜索下满足性质$ (\ast) $.

证  结合强Wolfe线搜索, (1.9)和(3.3)式, 再利用$ 0 < \gamma\leq\|g_{k}\|\leq\bar{\gamma} $和$ 0 < \sigma < \frac{\sqrt2}{2} $, 有

$ 0\leq\beta_{k}^{\rm IPRP}\leq \frac{\sigma \|g_k\|^2(1-|\cos\theta_{k}|)}{\|g_{k-1}\|^2}\leq \frac{\sigma \|g_{k}\|^2}{\|g_{k-1}\|^2}\leq\frac{\bar{\gamma}^2}{\gamma^2}. $

令$ b = \frac{\bar{\gamma}^2}{\gamma^2} > 1 $ 和$ \lambda = \frac{\gamma^4}{2\sqrt{2}L\bar{\gamma}^3} $, 则$ \beta_k^{\rm IPRP}\leq b $. 进而, 令$ \|s_{k-1}\| = \|\alpha_kd_k\|\leq\lambda $, 考虑到共轭参数公式(1.9), 假设(H1)和(H2), 可得

$ \begin{array}{lll}\beta_{k}^{\rm IPRP}&\leq { \sigma \frac{|(\|g_k\|^2-\frac{\|g_{k}\|}{\|g_{k-1}\|}|g_{k}^Tg_{k-1}|)|}{\|g_{k-1}\|^2}}\leq { \sigma \frac{|g_{k}^T(g_k-\frac{\|g_{k}\|}{\|g_{k-1}\|}g_{k-1})|}{\|g_{k-1}\|^2}}\\&\leq { \sigma \frac{\|g_{k}\|\left\|g_{k}-g_{k-1}+g_{k-1}-\frac{\|g_{k}\|}{\|g_{k-1}\|}g_{k-1}\right\|}{\|g_{k-1}\|^2}}\\ &\leq { \sigma\frac{\|g_{k}\|\|g_{k}-g_{k-1}\|+\|g_{k}\|\left|1-\frac{\|g_{k}\|}{\|g_{k-1}\|}\right|\|g_{k-1}\|}{\|g_{k-1}\|^2}} \\ & = { \sigma\frac{\|g_{k}\|\|g_{k}-g_{k-1}\|+\|g_{k}\| \left|\|g_{k-1}\|-\|g_{k}\| \right|}{\|g_{k-1}\|^2}}\\ &\leq { \frac{2\sigma\|g_{k}\|\|g_{k}-g_{k-1}\|}{\|g_{k-1}\|^2}}\\ &\leq { \frac{L\lambda\bar{\gamma}}{\gamma^2} = \frac{1}{2b}.} \end{array} $

证毕.

基于引理3.1, 3.2和3.3, 可建立IPRP方法的全局收敛性定理.

定理3.1  设假设(H1)和(H2)成立, 迭代点列$ \{x_k\} $由(1.1)和(1.2)式产生, 步长$ \alpha_k $满足强Wolfe线搜索准则(1.4), $ \beta_k $ 由(1.9)式产生, 则$ \lim\limits_{k\rightarrow \infty}\inf \|g_k\| = 0 $, 即IPRP方法是全局收敛的.

下面将分析IHS方法的搜索方向在强Wolfe线搜索下满足充分下降条件(3.1).

引理4.1   设假设(H2)成立, 且搜索方向$ d_{k} $由IHS方法产生. 若参数满足$ 0 < \sigma < 1 $, 则

(4.1) $ \begin{eqnarray} g_k^Td_k\leq-(1-\sigma)\|g_{k}\|^2, \ \forall \ k\geq1. \end{eqnarray} $

进而, 关系式$ 0\leq\beta_{k}^{\rm IHS}\leq\frac{g_k^Td_k}{g_{k-1}^Td_{k-1}} $ 成立.

证  利用数学归纳法证明. 当$ k = 1 $时, 有

$ g_1^Td_1 = -\|g_{1}\|^2<-(1-\sigma)\|g_{1}\|^2. $

假设对$ k-1 $有结论$ g_{k-1}^Td_{k-1}\leq-(1-\sigma)\|g_{k-1}\|^2 $成立. 往证其对$ k $的情形也成立. 由(1.2), (1.10), (3.3)和(3.5)式, 有

(4.2) $ \begin{eqnarray} g_k^Td_k& = &g_k^T(-g_k+\beta_{k}^{\rm IHS}d_{k-1}){}\\ & = &-\|g_k\|^2+\frac{\|g_{k}\|^{2}{\rm(1-|cos \theta_k|)}}{d_{k-1}^T(g_k-g_{k-1})}\cdot \frac{|g_{k}^T d_{k-1}|}{-g_{k-1}^T d_{k-1}}g_{k}^{T}d_{k-1}{}\\ & = &-\|g_k\|^2+\|g_{k}\|^{2}{\rm(1-|cos \theta_k|)}\frac{d_{k-1}^T(g_k-g_{k-1})+(g_{k-1}^{T}d_{k-1})}{d_{k-1}^T(g_k-g_{k-1})}\cdot\frac{|g_{k}^T d_{k-1}|}{(-g_{k-1}^{T}d_{k-1})}{}\\ &\leq&-(1-\sigma)\|g_k\|^2+\frac{\|g_{k}\|^{2}{\rm(1-|cos \theta_k|)}}{d_{k-1}^T(g_k-g_{k-1})}\cdot \frac{|g_{k}^T d_{k-1}|}{-g_{k-1}^T d_{k-1}}g_{k-1}^{T}d_{k-1}. \end{eqnarray} $

此外, 由归纳假设易知$ g_{k-1}^{T}d_{k-1} < 0 $. 这与强Wolfe非精确线搜索(1.4)的第二个不等式表明$ d_{k-1}^T(g_k-g_{k-1}) > 0 $. 因此, 由(4.2)式不难得到

$ g_k^Td_k\leq -(1-\sigma)\|g_k\|^2. $

进一步, 利用(3.3)和(4.2)式, 可得

(4.3) $ \begin{equation} {\large\begin{array}{ll}g_k^Td_k\leq \frac{\|g_{k}\|^{2}(1-|\cos \theta_k|)}{d_{k-1}^T(g_k-g_{k-1})}\cdot \frac{|g_{k}^T d_{k-1}|}{-g_{k-1}^T d_{k-1}}g_{k-1}^{T}d_{k-1} = \beta_{k}^{\rm IHS}(g_{k-1}^{T}d_{k-1}).\end{array}} \end{equation} $

将(4.3)式的两边同除以$ g_{k-1}^{T}d_{k-1} $, 有$ 0\leq\beta_{k}^{\rm IHS}\leq\frac{g_k^Td_k}{g_{k-1}^Td_{k-1}} $成立. 证毕.

最后, 可建立IHS方法的全局收敛性定理.

定理4.1   设假设(H1)和(H2)成立, 迭代点列$ \{x_k\} $由(1.1)和(1.2)式产生, 步长$ \alpha_k $满足强Wolfe线搜索准则(1.4), $ \beta_k $ 由(1.10)式产生, 则$ \lim\limits_{k\rightarrow \infty}\inf \|g_k\| = 0 $, 即IHS方法是全局收敛的.

证  由反证法. 若定理不成立, 注意到$ \|g_k\| > 0 $, 则存在常数$ \tilde{\gamma} > 0 $使得$ \|g_k\|^2\geq\tilde{\gamma}, \ \forall\ k. $ 由(1.2)式, 立得$ d_k+g_k = \beta_k^{\rm IHS}d_{k-1} $. 对上式两端取平方, 再结合引理4.1, 有

(4.4) $ \begin{eqnarray} \|d_k\|^2& = &(\beta_k^{\rm IHS})^2\|d_{k-1}\|^2-2g_k^Td_k-\|g_k\|^2{}\\ & \leq&\left(\frac{g_k^Td_k}{g_{k-1}^Td_{k-1}}\right)^2\|d_{k-1}\|^2-2g_k^Td_k-\|g_k\|^2. \end{eqnarray} $

将(4.4)式的两端同除以$ (g_k^Td_k)^2 $, 得

(4.5) $ \begin{eqnarray} \frac{\|d_k\|^2}{(g_k^Td_k)^2}&\leq&\frac{\|d_{k-1}\|^2}{(g_{k-1}^Td_{k-1})^2}-\frac{2}{g_k^Td_k}-\frac{\|g_k\|^2}{(g_k^Td_k)^2} {}\\& = &\frac{\|d_{k-1}\|^2}{(g_{k-1}^Td_{k-1})^2}-(\frac1{\|g_k\|}+\frac{\|g_k\|}{g_k^Td_k})^2+\frac1{\|g_k\|^2}{}\\ & \leq&\frac{\|d_{k-1}\|^2}{(g_{k-1}^Td_{k-1})^2}+\frac1{\|g_k\|^2}. \end{eqnarray} $

注意到$ \large\frac{\|d_1\|^2}{(g_1^Td_1)^2} = \frac1{\|g_1\|^2} $, 由(4.5)式和$ \|g_k\|^2\geq\tilde{\gamma} $, 有

(4.6) $ \begin{eqnarray} \frac{\|d_k\|^2}{(g_k^Td_k)^2}&\leq&\frac{\|d_{k-1}\|^2}{(g_{k-1}^Td_{k-1})^2}+\frac1{\|g_k\|^2}{}\\ &\leq&\frac{\|d_{k-2}\|^2}{(g_{k-2}^Td_{k-2})^2}+\frac1{\|g_{k-1}\|^2}+\frac1{\|g_k\|^2}{}\\ &\leq&\cdots \leq\sum\limits_{i = 1}\limits^k\frac{1}{\|g_i\|^2} \leq \frac{k}{\tilde{\gamma}}, \end{eqnarray} $

这意味着$ \frac{(g_k^Td_k)^2}{\|d_k\|^2}\geq\frac{\tilde{\gamma}}{k} $, 进而有

$ \sum\limits_{k = 1}\limits^\infty\frac{(g_k^Td_k)^2}{\|d_k\|^2} = \infty, $

这与引理3.1的Zoutendijk条件矛盾. 证毕.

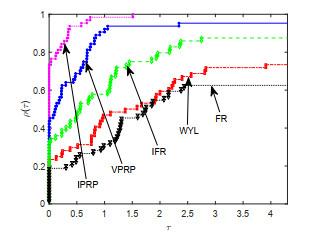
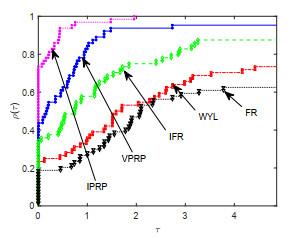
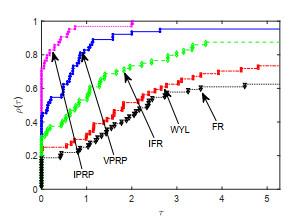
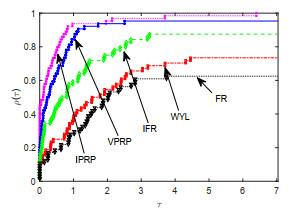
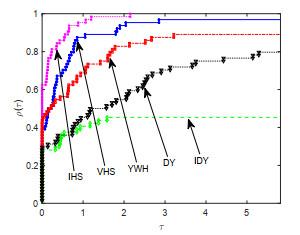
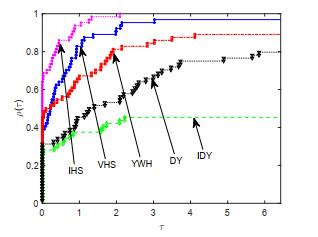
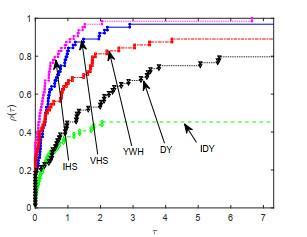
为检验该文所提出的IPRP和IHS方法的实际数值效果, 两种方法的数值试验都测试了64个问题, 所有算例均取自于无约束优化测试问题集^[16-17], 测试算例的规模从2到50000不等. 为便于比对数值效果, 将进行两组算法的数值试验, 即: 第一组为该文算法IPRP、算法FR^[2]、算法WYL^[6]、算法VPRP^[9]和算法IFR^[13]; 第二组为该文算法IHS、算法DY^[5]、算法YWH^[8]、算法VHS^[9]和算法IDY^[13]. 测试的环境为MATLAB R2017b, Windows 10操作系统, 计算机硬件为Inter(R) Core(TM) i5-8250U CPU 1.80 GHz和8 GB RAM. 所有测试都采用强Wolfe线搜索准则(1.4)获得步长, 参数选取为$ \delta = 0.01 $和$ \sigma = 0.1 $, 算法的终止准则为以下两种情形之一: (1) $ \|g_k\| < 10^{-5}; $ (2) 迭代次数大于1000次. 若终止准则(2)在试验中出现, 则认为该方法对这个数值例子失效, 并记为"F".

在试验中, 分别对所测试算法的迭代次数(Itr), 目标函数函数值计算次数(NF), 梯度计算次数(NG), 计算时间(Tcpu) (单位为秒)4个重要指标进行观测和比较, 并列出算法终止时目标函数梯度的2-范数($ \|g_k\| $), 数值结果详见表 1和表 2. 为进一步直观刻划试验效果, 将采用Dolan和Moré^[18]性能图进行比对. 图 1–4分别就算法IPRP、算法VPRP、算法WYL、算法IFR和算法FR在迭代次数、函数值计算次数、梯度计算次数及计算时间进行比较. 图 5–8分别就算法IHS、算法VHS、算法YWH、算法IDY和算法DY在迭代次数、函数值计算次数、梯度计算次数及计算时间进行比较.

从图 1–8可以更直观地看出, 算法IPRP和算法IHS在所考查的4个指标中均明显优于其他同类8个算法. 因此, 就数值试验的64个测试问题而言, 本文所提出的方法不仅在解决问题的个数上占据优势, 并且鲁棒性最优. 综上所述, 本文所修正的算法是有效的.