1 前言
对称正则长波方程
是用于描述弱非线性作用下离子声波和空间电荷波传播的数学模型[1-4]. 学者们对于对称正则长波方程(1.1)作了大量研究. 文献[5]中考虑了对称正则长波方程(1.1)初边值问题的整体解的存在性和唯一性. 文献[6]中利用径向基函数法求取了方程(1.1)的数值解. 此外, 文献[7-11]分别利用tanh函数扩展法、tanh-coth法、
文献[12]考虑了具有3次非线性项的广义对称正则长波方程组
的精确解求解问题. 文献[13]研究了具有两个非线性项的广义对称正则长波方程
的钟状孤波解的轨道稳定性问题, 并考虑了非线性项的相互作用对稳定性带来的影响. 本文我们将研究广义对称正则长波方程
型如
的孤波解和周期波解, 期待求出新解的同时我们将研究广义对称正则长波方程(1.4)的不同类型的解之间的演化关系. 首先, 我们利用平面动力系统的理论和方法对广义对称正则长波方程(1.4)型如(1.5)式的解进行定性分析, 给出在不同参数条件下有界行波解存在的条件. 接着, 我们将根据定性分析的结论, 用首次积分法求出广义对称正则长波方程的2类钟状孤波解, 1类扭状孤波解, 和7类椭圆函数周期波解. 文中最后还将考虑该方程所求得的孤波解, 扭状解与周期波解随Hamilton能量变化的演化关系. 值得指出: 本文用定性分析和首次积分相结合的方法, 不仅求出了广义对称正则长波方程(1.4)所有的钟状孤波解(单峰), 扭状解和周期解, 通过建立解与相图中有界轨线的对应关系赋予了所求解的数学意义. 更有意义的是文中还进一步揭示了广义对称正则长波方程的孤波解和周期波解与对应的Hamilton系统的能量之间的相互关系. 这是本文对比以往文献最明显的新颖之处.
2 定性分析
本节我们将利用平面动力系统理论和方法对广义对称正则长波方程(1.4) 的有界行波解做定性分析, 给出不同参数条件下的全局相图, 以及这种行波解存在性的若干结论.
设广义对称正则长波方程有型如(1.5)式的行波解. 把(1.5)式代入到方程(1.4)可得
将方程(2.1)的第二个等式代入第一个等式中, 并积分可得
其中
其中
故为研究方程(1.4)的孤波解和周期波解, 我们可以从方程(2.3)出发. 下面我们用平面动力系统的理论和方法对方程(2.3)进行定性分析.
令
在
设系统(2.4)存在三个有限远奇点
记系统(2.4)在
2.1 系统(2.4)的有限奇点
(1) 在
a)
(i) 当
因此,
(ii) 当
则有对应的Jacobi矩阵
故
b)
(i) 当
故
(ii) 当
故
c) 当
故
(2) 在
方程
a)
(i) 当
(ii) 当
b)
(i) 当
(ii) 当
c) 当
故
2.2 系统(2.4)的全局相图和方程(1.4)有界孤波解的存在性
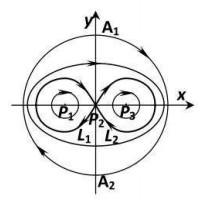
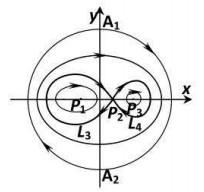
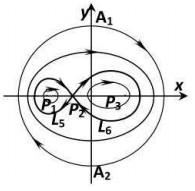
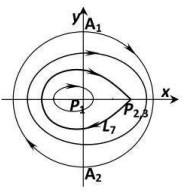
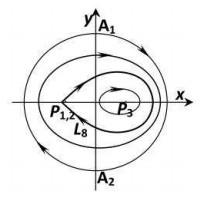
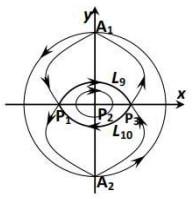
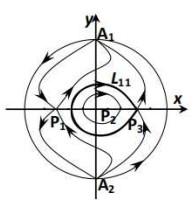
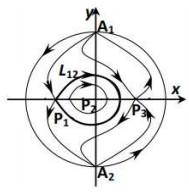
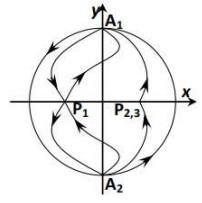
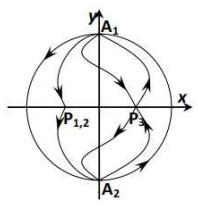
综合以上的定性分析, 我们可以得到不同参数下系统(2.4)的全局相图.
图 2.1
图 2.2
图 2.3
图 2.4
图 2.5
命题2.1 设
图 2.6
图 2.7
图 2.8
图 2.9
图 2.10
命题2.2 设
由于平面动力系统(2.4)的同宿轨对应于方程(1.4)的钟状解, 周期轨线对应于周期解. 故据性质2.1和性质2.2可得如下定理.
定理2.1 设
定理2.2 设
3 方程(1.4)孤波解的求解
在Hamilton系统中, 同一闭轨线上点的Hamilton能量
由系统(2.4)的首次积分(2.6)式, 可得
其中
其中
3.1 图 2.1–图 2.3对应的钟状孤波解
其中
将(3.3)式和(3.4)式代入(3.2)式, 则上述积分式可化为
当
于是, 当
当
由(3.7)和(3.8)式解出
上式中
综上, 我们可得如下定理.
定理3.1 假设
这里值得指出, 当
此时, 方程(1.4)有钟状孤波解
(3.13)式中的
3.2 图 2.7、图 2.8同宿轨线对应的孤波解
接下来我们考虑图 2.7中同宿轨对应的钟状孤波解的求解.
此时
其中
将(3.14)式代入(3.2)式, 并在
再考虑相图 2.8同宿轨线对应的钟状解. 此时
其中
将(3.17)式代入(3.2)式, 并在
综上, 我们可得如下定理.
定理3.2 设
(1) 当
其中
(2) 当
其中
3.3 相图 2.4、相图 2.5同宿轨线对应的孤波解
先考虑相图 2.4同宿轨对应的钟状解.
此时
又由
将(3.22)式代入(3.2)式, 并注意到此时
上式解出
又由
将(3.25)式代入(3.2)式, 并注意到
上式解出
综上可得如下定理.
定理3.3 设
(3.28)中
(3.29)式中
3.4 相图 2.6异宿轨线对应的扭状孤波解
此时
把(3.30)式代入(3.2)式, 有
由于此时
上式进一步关于
由此, 我们可得如下定理.
定理3.4 设
从而方程(1.4)有扭状孤波解
4 方程(1.4)的周期波解
下面我们考虑方程(1.4)的周期波解, 这里可以转化为求方程(2.3)的周期解, 即可以通过对方程(3.2)积分并做恰当的变换得到.
4.1 图 2.1和图 2.6中闭轨对应的精确周期波解
(1) 当
其中
此时
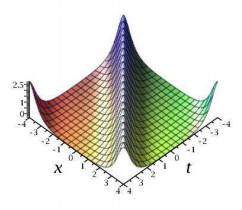
图 4.1
由于
此时(3.2)式可化为
令
在(4.3)式中令
其中模数
注4.1 当
其中
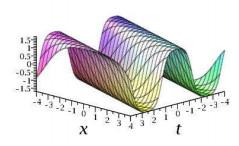
图 4.2
由于
设
对照引理4.2, 在(4.6)中令
其中模数
综上, 我们可以得到如下定理.
定理4.1 设
其中
其中
4.2 图 2.2–2.3周期轨线对应的精确周期波解
当
在
此时函数
由于
(i) 当
代入(3.2)式, 可得
这里
可得方程(2.3)的有界解
(ii) 当
与情形(i)类似可得到方程(2.5)的有界解
综上可得如下定理4.2.
定理4.2 设
和
其中
4.3 图 2.7–2.8周期轨线对应的精确周期波解
当
其中
时, (3.2)式中
(i) 当
可得方程(2.3)的有界解
这里
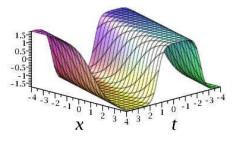
图 4.3
(ii) 当
可得方程(2.3)的有界解
这里
综上, 我们可以得到如下定理.
定理4.3 设
其中
其中
4.4 图 2.1–图 2.5其余周期轨线对应的周期波解
以
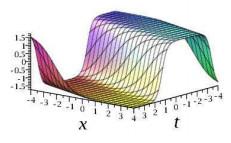
图 4.4
其中
将(4.24)式拆分为
其中
的两个实根. 由于
再令
化简可得方程(2.3)的有界解
其中
特别指出:
(1) 当
此时直接将(4.30)式代入(3.2)式, 求积分得到图 2.1中包围同宿轨线
其中
(2) 对比(4.23)式和(4.24)式, 可得
当
当
综上, 我们可以得到如下定理.
定理4.4 若条件(1):
5 方程(1.4)孤波解和周期波解的演化关系
文中第3节已求出了方程(1.4)的两种形式的钟状孤波解, 第4节又求出了方程(1.4)在不同参数条件下的精确周期波解. 本节我们将研究方程(1.4)的孤波解与周期波解的演化关系, 揭示方程(1.4)对应的Hamilton系统的能量变化对解波形的影响. 本节我们假定
5.1 方程(1.4)的周期波解、孤波解与Hamilton能量取值的关系
因为平面动力系统(2.4)是Hamilton系统, 在同一闭轨上点的Hamilton能量相等. 在参数不变
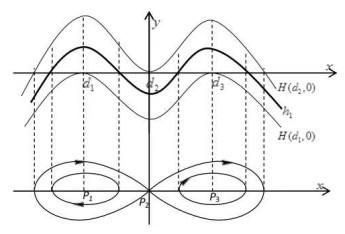
下面我们以全局相图 2.2为例, 讨论(1.4)式的行波解与其对应的Hamilton能量取值的关系.
此时
据在第3节和第4节中讨论的孤波解, 周期波解与全局相图中同宿轨线和周期轨线的对应关系, 可以推得, 当
(1) 当
(2) 当
(3) 当
(4) 当
(5) 当
综上可得, 当
5.2 方程(1.4)的周期波解和孤波解与Hamilton能量取极限的关系
5.2.1 相图 2.1对称同宿轨内周波解与孤波解的演变关系
当
故有
即, 当Hamilton能量
5.2.2 相图 2.6对称异宿轨内周波解与孤波解的演变关系
全局相图 2.6有对称异宿轨
故
即当Hamilton能量
5.2.3 非对称同宿轨内周期波解和孤波解的演变关系
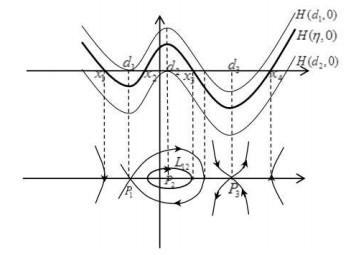
(1) 在相图 2.3情形
此时
此时, 系统(2.4)有3个奇点
如图 5.1所示, 当
图 5.1
显然,
当Hamilton能量
且
由于函数
同理可得
故当
(2) 在相图 2.8情形
此时
故由函数的连续性知, 当
故当
5.2.4 包围同宿轨的闭轨对应的周期波解与孤波解的极限关系
本段我们仅以相图 2.3中包围同宿轨的闭轨为例进行讨论, 其余情形类似.
此时
如图 5.1所示, 此时有
当
由此可得
故当
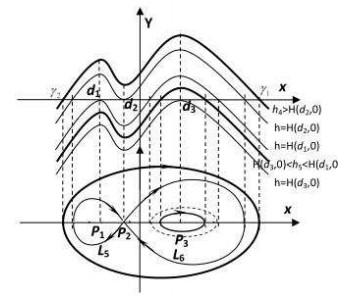
5.3 周期波解向孤波解演变的示意图
综合前面的讨论我们知道随着系统(2.4)的Hamilton能量变化, 方程(1.4)的周期波解会逐渐演变成孤波解. 本节我们选取方程(1.4)的两个周期波解, 展示出当能量
(1) 当
现令
当Hamilton能量
图 5.2
图 5.3
图 5.4
图 5.5
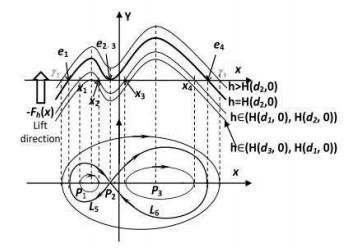
(2) 当
我们只需画出当
图 5.6
图 5.7
图 5.8
图 5.9
6 结论
本文我们运用平面动力系统定性分析和首次积分法相结合的方法, 求出了广义对称正则长波方程(1.4)在各种不同条件下具有的全部周期波解, 孤波解和扭状解, 尤其是求出了非对称同宿轨线所围的闭轨对应的周期解及包围同宿轨线的闭轨对应的周期解. 讨论了当Hamilton能量变化时方程的周期波解和孤波解演变关系, 揭示出所研方程之所以会出现周期波解和孤波解, 本质上是由方程(2.3)所对应的Hamilton系统的能量
本文所用的定性分析与首次积分相结合的方法, 直观地展示了所求的解与全局相图中轨线的相互对应关系, 便于揭示方程所对应的Hamilton系统的能量与方程的周期波解和孤波解的联系. 本文的方法与结果可直接可应用于其它非线性发展方程的孤波解、周期波解的求解及相关问题的研究.
参考文献
A symmetric regularized long wave equation
DOI:10.1063/1.864487 [本文引用: 1]
Cascade evolution of spherically symmetric pulsons in multivacuum field theory models
DOI:10.1016/0375-9601(77)90138-4
Dynamics of classical solitons (in non-integrable systems)
DOI:10.1016/0370-1573(78)90074-1
Computer simulation and analysis for the spherical and cylindrical ion-acoustic solitons
DOI:10.1143/JPSJ.41.257 [本文引用: 1]
The initial boundary value problem for symmetric long wave equations with nonhomogeneous boundary value
Numerical solutions of the symmetric regularized long wave equation using radial basis functions
Traveling solitary wave solutions for the symmetric regularized long-wave equation
DOI:10.24297/jam.v11i8.1206 [本文引用: 1]
Exact travelling wave solutions of the symmetric regularized long wave (SRLW) using analytical methods
Applications of exact traveling wave solutions of modified Liouville and the symmetric regularized long wave equations via two new techniques
DOI:10.1016/j.rinp.2018.04.039
An exponential wave integrator pseudospectral method for the symmetric regularized-long-wave equation
Generalized Jacobi elliptic function method for periodic wave solutions of SRLW equation and (1+1)-dimensional dispersive long wave equation
具5次强非线性项的广义对称正则长波方程的显式精确解
Precise and explicit solutions to a generalized symmetric regularized long wave equations with five order stronger nonlinear term
Orbital stability of solitary waves for generalized symmetric regularized-long-wave equations with two nonlinear terms