1 引言
Parisian破产的概念最初来自于Parisian期权. 从Dassios和Wu[7]以来, Parisian破产在保险精算学中引起了广泛的关注. 如果保险公司的盈余水平在一段连续的时间内一直低于一个我们给定的盈余水平, 我们就说Parisian破产发生了. Parisian破产有两种定义, 一种是固定时间的延迟(参见文献[6, 20, 23, 25]). 另一种是随机时间的延迟(参见文献[4, 8-9, 12-13]). Lkabous和Renaud[19]将以上两种延迟进行了整合并称之为混合延迟. Li等[14]基于混合观测体系重新定义了Parisian破产问题, 并且得到了Parisian破产概率的具体表达式及其极限形式. 最近, Lkabous[17]将Li等[14]的结果进行了推广并得到了一些其他的波动等式. 在此, 我们指出Li等[14]只给出了破产概率的表达式, Lkabous[17]只讨论了当
受上面这些文献的启发, 在本文中, 我们继续在谱负Lévy风险模型下研究基于混合观测体系的Parisian破产问题, 并且讨论破产时间和赤字的联合拉普拉斯变换. 本文结构如下: 在第2节中, 我们给出模型并简单的介绍谱负Lévy过程和尺度函数; 在第3节中, 给出主要结果及证明; 在第4节中, 给出一个例子.
2 模型
在本文中, 我们考虑风险盈余过程
其中
是过程
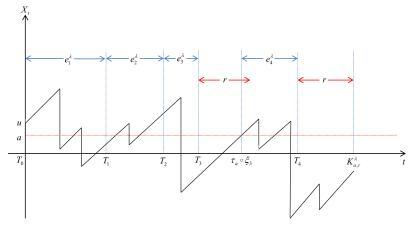
图 1
下面, 我们定义一些符号. 首先, 过程
我们将首次观测到过程的盈余水平小于0的时间定义为
其中
其中
其中
在此, 我们指出
其中
当
Albrecher等[2]定义了尺度函数
这允许我们给出更一般的结论. 由Kyprianou[11], 我们知道当
由(2.3)和(2.6) 式, 可以得到
并且对任意的
为了简单起见, 当
众所周知
并且
Lkabous和Renaud[19]定义了
它也可以被写为
当
详见Loeffen等[21], 并且我们记
3 主要结果及证明
在这一章中, 我们讨论
定理3.1 当
其中
注3.1 当
定理3.1的证明 对
在(3.2) 式中令
将(3.3) 式代入(3.2) 式, 有
由(2.1) 式, 为了证明我们的结果, 我们只需计算
一方面, 由文献[11], 有
由(2.3) 式, (3.6) 式以及Fubini定理很容易得到
当
由文献[20], 有
因此, 由(2.8) 式和(3.9) 式得
当
结合(3.11) 式和(3.10) 式可以得到
类似的, 有
将(3.12)和(3.13) 式代入(3.8) 式, 得到
接下来我们讨论(3.14) 式的拉普拉斯逆变换. 当
以及
类似的
因此, 由(3.15) 式, (3.16) 式以及(3.17) 式, 有
最后, 将(2.1) 式和(3.18) 式代入(3.4) 式就得到了(3.1) 式. 证毕.
接下来, 我们利用Lkabous[17]中的定理3的结论和测度变换法讨论
定理3.2 当
其中
证 由文献[11], 我们知道, 对任意的
是鞅. 对任意的
此外, 当
其中
并且
此外, 当
其中
为了得到(3.19) 式的具体表达式, 我们需要得到
的具体表达式. 首先, 我们可以很容易得到
而
对
其中第一个和第四个等式中分别用到了Fubini定理和(2.11) 式, 第二个等式中用到了Kendall等式[5],
由文献[11] 中首达时
得到了第四个等式. 与此同时
由拉普拉斯变换的唯一性, 可知
换句话说, 也就是
将(3.20) 式和(3.23) 式代入(3.19) 式, 并结合
定理3.2证毕.
推论3.1 当
其中
注3.2 当
推论3.1的证明 我们首先注意到
由式(2.4) 式, (2.9) 式和(3.24) 式, 有
推论3.1证毕.
推论3.2 在定理
证 由(3.17) 式, (2.14) 式以及Fubini定理可得
其中
其中第二个等式中用到了(2.8) 式. 由于
以及
所以, 可以得到
由拉普拉斯变换的唯一性, 可知
因此
推论3.2证毕.
4 例子
本章在特殊的Lévy风险模型: Brownian风险模型下给出了Parisian破产时盈余的拉普拉斯变换. 令
其中
下面, 我们计算破产时盈余的拉普拉斯变换. 由
由(2.2) 式, 有
由
其中
此外
通过一些计算, 我们得到
其中
与此同时, 我们有
将(4.1) 式, (4.2) 式和(4.3) 式相加, 可得
因此, 我们有
由定理3.1, 可得
其中
参考文献
Randomized observation times for the compound Possion risk model: The discounted penalty function
DOI:10.1080/03461238.2011.624686
Exit identities for Lévy processes observed at Poisson arrival times
Pricing of Parisian options for a jump-diffusion model with two-sided jumps
DOI:10.1080/1350486X.2011.599976
Gerber-Shiu distribution at Parisian ruin for Lévy insurance risk processes
DOI:10.1017/jpr.2016.21 [本文引用: 2]
Ruin Probability with Parisian delay for a spectrally negative Lévy process
DOI:10.1017/S0021900200008573 [本文引用: 1]
On barrier strategy dividends with Parisian implementation delay for classical surplus process
DOI:10.1016/j.insmatheco.2009.05.013 [本文引用: 1]
Spectrally negative Lévy risk model under Erlangized barrier strategy
DOI:10.1016/j.cam.2018.11.001 [本文引用: 1]
On a spectrally negative Lévy process with periodic dividends and capital injections
DOI:10.1016/j.spl.2019.108589 [本文引用: 1]
An insurance risk model with Parisian implementation delays
DOI:10.1007/s11009-012-9317-4 [本文引用: 2]
Occupation times of spectrally negative Lévy processes with applications
DOI:10.1016/j.spa.2011.07.008 [本文引用: 3]
A temporal approach to the Parisian risk model
DOI:10.1017/jpr.2018.18 [本文引用: 6]
The joint Laplace transform for diffusion occupation times
On pre-exit joint occupation times for spectrally negative Lévy processes
A note on Parisian ruin under a hybrid observation scheme
DOI:10.1016/j.spl.2018.09.013 [本文引用: 5]
Parisian ruin for a refracted Lévy process
DOI:10.1016/j.insmatheco.2017.03.005
A unified approach to ruin probabilities with delays for spectrally negative Lévy processes
DOI:10.1080/03461238.2019.1598890 [本文引用: 2]
Parisian ruin probability for spectrally negative Lévy processes
Discounted penalty function at Parisian ruin for Lévy insurance risk process
DOI:10.1016/j.insmatheco.2017.10.008 [本文引用: 1]
Occupation times of intervals until first passage times for spectrally negative Lévy processes
DOI:10.1016/j.spa.2013.11.005 [本文引用: 1]
On the time value of Parisian ruin in (dual) renewal risk process with exponential jumps
折射Lévy风险过程的Parisian破产问题
DOI:10.3969/j.issn.1003-3998.2019.01.018
On the Parisian ruin probability in a refracted Lévy process
DOI:10.3969/j.issn.1003-3998.2019.01.018
On spectrally positive Lévy risk processes with Parisian implementation delays in dividend payments
DOI:10.1016/j.spl.2018.05.013 [本文引用: 1]