1 引言
联系在一起, 其中
若
这个非局部NLS方程(1.3) 与
综上所述, 对于Alice-Bob系统有许多有趣的工作可以做. 本文研究Alice-Bob-NLS系统(AB-NLS)[1]
其中
的一个特殊对称约化. 若
文章首先利用Hirota方法给出未约化的AB-NLS系统(5)的双线性Bäcklund变换; 然后构建约化的AB-NLS系统(1.4) 的
2 双线性Bäcklund变换
Bäcklund变换在孤子系统的研究中起着重要的作用[21]. 本节研究未约化的AB-NLS系统(1.5) 的双线性Bäcklund变换(BT). 首先, 引入双线性变换
其中
其中
通过Hirota双线性
其中
定理 2.1 如果
其中
证 考虑如下表达式
只需利用定理中的方程(2.8)–(2.14) 使其能推导得到
接着证明
最后证明
证毕.
定理中的方程(2.8)–(2.14) 就是方程(2.2) 的双线性BT.
3 Darboux变换
方程(1.4) 的可积性由方程(1.5) 的可积性保障, 且方程(5)具有如下Lax对
通过下面的规范变换
方程(3.1)和(3.2) 可转化为
用新势
令
其中
根据方程(1.4) 中
为了确定(3.6) 式中的
其中
我们可以证明仅当
经过
其中
在方程(3.14) 中,
其中
且矩阵
通过
4 孤子解
本节利用上面获得的DT来构建方程(1.4) 的孤子解. 易证方程(1.4) 具有如下形式的解
其中
4.1 1-孤子解
设方程(3.1)–(3.2)中
由方程(3.10), 可得
由方程(3.11) 与(4.3), 可得
如果在(3.16) 式中取
其中
为了更好地理解该孤子解的动力学性质, 我们通过(4.5) 式的不同情形对上面的1 -孤子解做进一步分析.
情形1
在此情形下1 -孤子解(4.6) 为
为了保证解(4.7) 的解析性即不含有任意奇点, 必须使
其中
因此, 解(4.7) 必须满足如下条件
显然, 当
若令
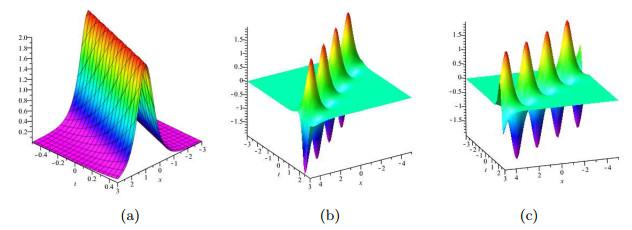
图 1
图 1
(4.12)式中参数取
(a) 为解的模, (b) 和(c) 分别为解的实部和虚部
若令
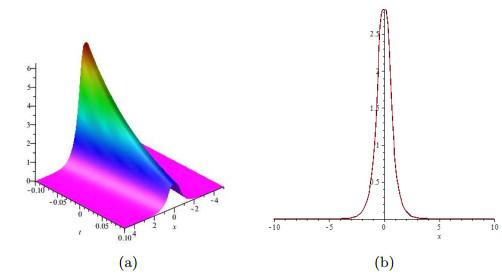
该解的时空结构如图 2所示, 由该图观察到势函数是沿着
图 2
如果设
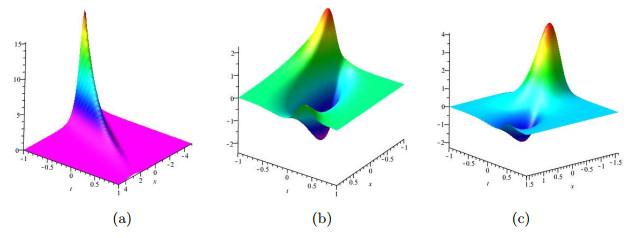
该解的时空结构如图 3所示, 观察该图发现势函数也沿着
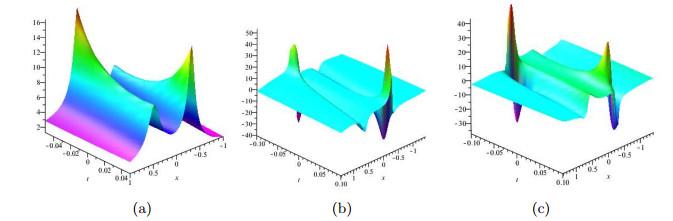
图 3
图 3
(4.14) 式中参数取
(a)为解的模, (b) 和(c) 分别为解的实部和虚部
类似地, 可讨论
情形2
在此情形下, 1 -孤子解(4.6) 为
当
时, 解(4.15) 有无穷多奇点
且
情形3
在此情形下, 1 -孤子解(4.6) 为
当
时, 解(4.18) 有无穷多奇点
同时
4.2 2-孤子解
下面我们依然选取零种子解
其中
且
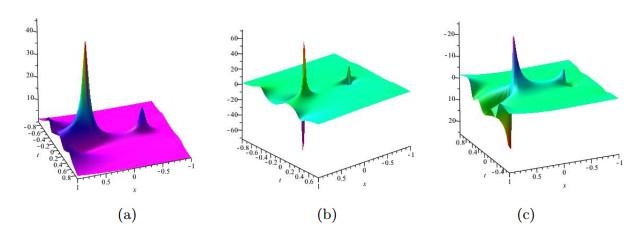
通过确定解(4.21) 中的参数值, 可得图 4, 其展示了该解的3 -维演化图.
图 4
图 4
(4.21)式中参数取
(a) 为该解的模, (b) 和(c) 分别为解(57) 的实部和虚部
通过2阶DT, 如果令
其中
图 5
令
其中
该复数解(4.23)的演化图在此省略.
5 结论
本文所讨论的AB-NLS系统只是楼森岳最近提出的众多AB系统中的一个. 众所周知, 非线性Schrödinger (NLS) 方程仅有解
参考文献
Alice-Bob systems,
DOI:10.1063/1.5051989 [本文引用: 5]
Alice-Bob physics: coherent solutions of nonlocal KdV systems
DOI:10.1038/s41598-017-00844-y [本文引用: 1]
Integrable nonlocal nonlinear Schrödinger equation
DOI:10.1103/PhysRevLett.110.064105 [本文引用: 1]
Prohibitions caused by nonlocality for nonlocal Boussinesq-KdV type systems
Solitons and dynamics for a general integrable nonlocal coupled nonlinear Schrödinger equation
DOI:10.1016/j.cnsns.2016.09.013 [本文引用: 1]
Soliton solutions of an integrable nonlocal modified Korteweg-de Vries equation through inverse scattering transform
DOI:10.1016/j.jmaa.2017.04.042 [本文引用: 1]
Integrable discrete PT symmetric model
DOI:10.1103/PhysRevE.90.032912 [本文引用: 1]
Davey-Stewartson type equations in 4+2 and 3+1 possessing soliton solutions
Making sense of non-Hermitian Hamiltonians
DOI:10.1088/0034-4885/70/6/R03 [本文引用: 1]
Experimental observation of the dual behavior of PT-symmetric scattering
DOI:10.1103/PhysRevA.85.050101 [本文引用: 1]
Optical solitons in PT periodic potentials
DOI:10.1103/PhysRevLett.100.030402
Observation of parity-time symmetry in optics
DOI:10.1038/nphys1515 [本文引用: 1]
Breather, lump and X soliton solutions to nonlocal KP equation
DOI:10.1016/j.camwa.2017.07.004
Rational and semirational solutions of the nonlocal davey-Stewartson equations
DOI:10.1111/sapm.12178 [本文引用: 1]
On a nonlocal modified Korteweg-de Vries equation: Integrability, Darboux transformation and soliton solutions
DOI:10.1016/j.cnsns.2016.06.015 [本文引用: 1]
Nonlocal modified KdV equations and their soliton solutions
DOI:10.1016/j.cnsns.2018.07.013 [本文引用: 1]
(2+1) Dimensional local and nonlocal reductions of the negative AKNS system: soliton solutions
DOI:10.1016/j.cnsns.2018.11.016 [本文引用: 1]
Rogue waves in the (2+1) dimensional nonlinear Schrödinger equation with a parity-time-symmetric potential
DOI:10.1088/0256-307X/34/1/010202 [本文引用: 1]
Integrable nonlocal asymptotic reductions of physically significant nonlinear equations
Integrable nonlocal nonlinear equations
A bilinear Bäcklund transformation of a (3+1)-dimensional generalized KP equation
DOI:10.1016/j.aml.2012.01.003 [本文引用: 1]
Nonlocal nonlinear Schrodinger equations and their soliton solutions
Soliton solutions for the nonlocal nonlinear Schrödinger equation
Rational solitons in the parity-time-symmetric nonlocal nonlinear Schrödinger model
Exact solutions of (2+1)-dimensional Euler equation found by weak Darboux transformation
DOI:10.1088/0256-307X/23/10/003
Darboux transformation and analytic solutions of the discrete PT-symmetric nonlocal nonlinear Schrödinger equation
On N th-order rogue wave solution to nonlinear coupled dispersionless evolution equations
DOI:10.1016/j.physleta.2012.09.050 [本文引用: 1]