环图上Sturm-Liouville算子的部分反谱问题

环图上Sturm-Liouville算子的部分反谱问题

官声玉^,¹, 吴东杰¹, MuratSat², 杨传富¹

A Partial Inverse Problem for the Sturm-Liouville Operator on Quantum Graphs with a Loop

Guan Shengyu^,¹, Wu Dongjie¹, Murat Sat², Yang Chuanfu¹

通讯作者: Murat Sat杨传富

收稿日期: 2020-01-14

基金资助:

国家自然科学基金. 11871031
江苏省自然科学基金. BK20201303

Received: 2020-01-14

Fund supported:

the NSFC. 11871031
the Jiangsu NCF. BK20201303

作者简介 About authors

官声玉,E-mail:guanshengyu@njust.edu.cn , E-mail：guanshengyu@njust.edu.cn

Abstract

This deals with the Sturm-Liouville operator on the quantum graphs with a loop. Given the potential on a part of edges, we try to recover the remaining potential from the subspectrum. The uniqueness theorem and a constructive algorithm for the solution of this partial inverse problem are provided.

Keywords： Partial inverse spectral problem ; Sturm-Liouville operator ; Quantum graph ; Riesz-basis

PDF (278KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

官声玉, 吴东杰, MuratSat, 杨传富. 环图上Sturm-Liouville算子的部分反谱问题. 数学物理学报[J], 2021, 41(2): 289-295 doi:

Guan Shengyu, Wu Dongjie, Murat Sat, Yang Chuanfu. A Partial Inverse Problem for the Sturm-Liouville Operator on Quantum Graphs with a Loop. Acta Mathematica Scientia[J], 2021, 41(2): 289-295 doi:

1 引言

量子图上微分算子是现代数学物理研究的一个重要方向. 该模型的重要性出现在碳纳米结构、声学和光子晶体理论研究中^{[1, 6-7, 11-12]}. 本文主要是构造量子图上Sturm-Liouville算子中的未知势函数. 这个问题在星型图上已经解决^{[2, 8-9]}. 本文考虑带环量子图：在假定两条边上的势函数是已知的情况下去重构剩余未知势函数. 杨和Bondarenko^[10]考虑了带有一个环的套索图. 在此基础上, Bodarenko和Shieh又研究了具有一个环和 $n-1$ 条边的量子图, 利用Riesz基和Weyl函数得到了部分反问题的唯一性定理和构造解^[3].

本文在量子环图上考虑除环外所有边的势函数都是已知的Sturm-Liouville算子. 讨论其特征值的渐近式, 唯一性定理及重构算法。

2 环图上微分算子

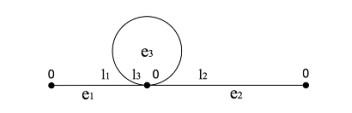
考虑如下由一环和两条边构成的量子图 $G$ . 各条边的长度分别为 $l_1 = 1, l_2 = 2, l_3 = 3.$ 引入参数 $x_j\in[0, l_j], j = \overline{1, 3}$ , 且在边界顶点处满足 $x_1 = x_2 = 0$ , 在顶点处满足 $x_1 = 1,$ $x_2 = 2,$ $x_3 = 0,$ 和 $x_3 = 3$ .

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1 量子环图

在图 $G$ 上研究Sturm-Liouville边值问题 $L$

$\begin{eqnarray} &-y''_{j}(x_j)+q_j (x_j)y_j (x_j) = \lambda y_j(x_j), x_j \in (0, l_j) , j = 1, 2, 3, \end{eqnarray}$

(2.1)

$\begin{eqnarray} &y_1(0) = y_2(0) = 0, \end{eqnarray}$

(2.2)

$\begin{eqnarray} &y_{1}(1) = y_{2}(2) = y_{3}(3) = y_{3}(0), \end{eqnarray}$

(2.3)

$\begin{eqnarray} &y'_{1}(1)+y'_{2}(2)+y'_{3}(3) = y'_{3}(0). \end{eqnarray}$

(2.4)

这里 $\lambda$ 为谱参数, $q_j \in L^2[0, l_j]$ 且是实的.

定义2.1 令 $B_{2, a}$ 为指数不大于a的Paley-Wienner函数. 符号 $\kappa_{k, odd}(\rho), \kappa_{k, even}(\rho)$ 分别表示属于 $B_{2, a}$ 的奇、偶函数

$\begin{eqnarray} \kappa_{k, odd}(\rho) = \int^{k}_{0}K(t)\sin\rho t{\rm d}t, \ \ \ \ \kappa_{k, even}(\rho) = \int^{k}_{0}N(t)\cos\rho t{\rm d}t. \end{eqnarray}$

记 $C_j(x_j, \lambda), S(x_j, \lambda)$ 为等式(2.1) 满足初值条件: $C_j(0, \lambda) = S'_j(0, \lambda) = 1,$ $C'_j(0, \lambda) = \\S_j(0, \lambda) = 0$ 下的解, 则由文献[4]得到如下关系式

$\begin{equation} \left\{ \begin{array}{ll} { } C_j(l_j, \rho) = \cos \rho l_j+\kappa_{l_j, even}(\rho), \\ { } S_j(l_j, \rho) = \frac{\sin \rho l_j}{\rho}+\frac{\kappa_{l_j, odd}(\rho)}{\rho}, \\ S'_j(l_j, \rho) = \cos \rho l_j+\kappa_{l_j, even}(\rho). \end{array} \right. \end{equation}$

(2.5)

3 特征值分布

研究边值问题 $L$ 的特征值, 需研究示性函数的性质. 示性函数

$\begin{eqnarray} \Delta(\lambda) = &S_1(1, \lambda)S_2(2, \lambda)[2-C_3(3, \lambda)-S'_3(3, \lambda)] \\ &-[S'_1(1, \lambda)S_2(2, \lambda)+S_1(1, \lambda)S'_2(2, \lambda)]S_3(3, \lambda). \end{eqnarray}$

(3.1)

下面我们考虑它的零点的分布情况, 基于儒歇定理([4], 定理1.1.3)及渐近分析有如下引理.

引理3.1 问题 $L$ 特征值为 $\{\lambda_{nk}\}_{n\in {\Bbb Z}, k = 1, 2}\bigcup\{\lambda^{(i)}_{n3}\}_{n\in {\Bbb Z}, i = 1, 2}\bigcup \{\lambda^{(i)}_{n4}\}_{n\in{\Bbb N}, i = 1, 2}$ , 且满足

$\begin{equation} \left\{ \begin{array}{ll} \rho_{nk} = \sqrt{\lambda_{nk}} = |2\pi n+\alpha_k|+{\kappa_n}, \ \ \ &n\in{\Bbb Z}, k = 1, 2, \\ \rho^{(i)}_{n3} = \sqrt{\lambda^{(i)}_{n3}} = |2\pi n+\alpha_3|+{\kappa_n}, \ \ \ & n\in{\Bbb Z}, i = 1, 2, \\ \rho^{(i)}_{n4} = \sqrt{\lambda^{(i)}_{n4}} = n\pi+{\kappa_n}, \ \ \ & n\in{\Bbb N}, i = 1, 2, \end{array} \right. \end{equation}$

(3.2)

其中 $\alpha_1 = \arccos\frac{2+\sqrt{2}}{4}, \alpha_2 = \arccos\frac{2-\sqrt{2}}{4}, \alpha_3 = \frac{2\pi}{3}$ .

4 部分反问题唯一性定理

选择子谱 $\Lambda: = \{\lambda_{nk}\}_{n\in{\Bbb Z}, k = 1, 2}$ , 记符号 ${\cal I} = \{(n, j): \rho_{nj}\in\Lambda\}$ . 本文假设

(1) $\Lambda$ 中所有特征值是不同的;

(2) $\Lambda$ 中所有特征值是正的;

(3) 对于 $\lambda_{nj}\in\Lambda$ , $S_1(1, \lambda_{nj})S_2(2, \lambda_{nj})S_3(3, \lambda_{nj})\neq0$ .

在假设(1)–(3)下, 研究如下反问题.

反问题: 给定势函数 $q_2, q_3$ , 和子谱 $\Lambda$ , 重构函数 $q_1$ .

由关系式(3.2), 得到

$\begin{equation} \left\{ \begin{array}{lr} { } S_1(1, \rho) = \frac{\sin\rho}{\rho}+\frac{1}{\rho}\int^{1}_{0}K(t)\sin\rho t{\rm d}t, \\ { } S'_1(1, \rho) = \cos \rho+\int^{1}_{0}N(t)\cos\rho t{\rm d}t, \end{array} \right. \end{equation}$

(4.1)

其中函数 $K, N$ , 是属于 $L_2(0, 1)$ 的实函数. 将此式代入(3.1)式, 得到

$\begin{eqnarray} \int^{1}_{0}K(t)a_{nj}\sin\rho_{nj} t{\rm d}t+\int^{1}_{0}N(t)b_{nj}\cos\rho_{nj} t{\rm d}t = f_{nj}, \ \ \ \ (n, j)\in{\cal I}, \end{eqnarray}$

(4.2)

$\begin{eqnarray} a_{nj}& = &[2S_2(2, \lambda_{nj})-S_2(2, \lambda_{nj})C_3(3, \lambda_{nj})-S'_2(2, \lambda_{nj})S_3(3, \lambda_{nj}) {} \\ &&-S_2(2, \lambda_{nj})S'_3(3, \lambda_{nj})]\rho_{nj}, {} \\ b_{nj}& = &-S_2(2, \lambda_{nj})S_3(3, \lambda_{nj})\rho^2_{nj}, {} \\ f_{nj}& = &-a_{nj}\sin\rho_{nj}-b_{nj}\cos\rho_{nj}. \end{eqnarray}$

(4.3)

记

$\begin{eqnarray} f(t) = \left[ \begin{array}{c} K(t)\\ N(t) \end{array} \right], v_{nj}(t) = \left[ \begin{array}{c} a_{nj}\sin\rho_{nj}t\\ b_{nj}\cos\rho_{nj}t \end{array} \right], (n, j)\in{\cal I}, \end{eqnarray}$

(4.4)

设向量函数 $g$ , $h$ 是属于Hilbert空间 ${\cal H}$ , 则在空间 $H$ 上内积为

$\begin{eqnarray*} (g, h) = \int^{1}_{0}\Big(g_1(t)h_1(t)+g_2(t)h_2(t)\Big){\rm d}t, {\nonumber} \\ g = \left[ \begin{array}{c} g_1\\ g_2 \end{array} \right], \quad h = \left[ \begin{array}{c} h_1\\ h_2 \end{array} \right], g, h\in{\cal H}. \end{eqnarray*}$

向量函数 $v_{nk}$ , $f$ 属于实Hilblet空间 ${\cal H}: = L_2(0, 1)\oplus L_2(0, 1)$ , (4.2)式可写为

$\begin{eqnarray} (f, v_{nj})_{{\cal H}} = f_{nj}, \ \ \ \ (n, j)\in{\cal I}. \end{eqnarray}$

(4.5)

引理4.1 向量函数系 $V = \{v_{nj}\}_{(n, j)\in{\cal I}}$ 在 $H$ 中完备.

证(反证法) 设存在 $w_1, w_2\in L_2(0, 1)$ , 使得

$\begin{eqnarray} \int^{1}_{0}w_1(t)a_{nj}\sin\rho_{nj} t{\rm d}t+\int^{1}_{0}w_2(t)b_{nj}\cos\rho_{nj} t{\rm d}t = 0, \ \ \ \ (n, j)\in{\cal I}, \end{eqnarray}$

(4.6)

由假设(3) 和(3.1)式, 可知

$\begin{eqnarray*} a_{nj} = -\frac{S'_1(1, \lambda_{nj})b_{nj}}{\rho_{nj}S_1(1, \lambda_{nj})}. \end{eqnarray*}$

再将此式代入(4.6)式, 有

$\begin{eqnarray} \int^{1}_{0}\Big(w_1(t)S'_1(1, \lambda_{nj})\frac{\sin\rho_{nj} t}{\rho_{nj}}-w_2(t)S_1(1, \lambda_{nj})\cos\rho_{nj} t\Big){\rm d}t = 0, \end{eqnarray}$

(4.7)

即

$\begin{eqnarray} W(\lambda): = \int^{1}_{0}\Big(w_1(t)S'_1(1, \lambda)\frac{\sin\rho t}{\rho}-w_2(t)S_1(1, \lambda)\cos\rho t\Big){\rm d}t \end{eqnarray}$

(4.8)

的零点为 $\Lambda$ . 结合(4.1)式, 有估计式

$\begin{eqnarray} W(\lambda): = O\Big(\frac{e^{2|Im\rho|}}{|\rho|}\Big), \ \ \ \ |\rho|\rightarrow \infty. \end{eqnarray}$

(4.9)

在假设(1)–(2)下构造无穷乘积

$\begin{eqnarray} D(\lambda) = \prod\limits_{\lambda_{nj}\in\Lambda}\Big(1-\frac{\lambda}{\lambda_{nj}}\Big). \end{eqnarray}$

(4.10)

易知 $\frac{W(\lambda)}{D(\lambda)}$ 是整函数, 再由渐近式(3.2), 函数 $D(\lambda)$ 可表示为

$\begin{eqnarray} D(\lambda) = C\prod\limits_{k = 1}^{2}(\cos \rho-\cos\alpha_k)+\kappa_{2, even}(\rho), \end{eqnarray}$

(4.11)

这里 $C$ 是非零常数, 而且对于正数 $\varepsilon$ , $\rho^*$ , 我们有估计式

$\begin{eqnarray} |D(\rho^2)|\geq Ce^{2|Im\rho|}, \ \ \ \ \varepsilon<\arg\rho<\pi-\varepsilon, \ \ \ \ |\rho|\geq\rho^*, \end{eqnarray}$

(4.12)

因此结合(4.9)式得到

$\begin{eqnarray} \frac{W(\lambda)}{D(\lambda)} = o(1), \ \ \ \ \lambda = \rho^2, \ \ \ \ \varepsilon<\arg\rho<\pi-\varepsilon, \ \ \ \ |\rho|\geq\rho^*. \end{eqnarray}$

(4.13)

这里我们注意到若 $\{\xi_n\}_{n\in{\Bbb N}}$ , $\{\eta_n\}_{n\in{\Bbb N}\cup\{0\}}$ 分别是 $S_1(1, \lambda)$ 和 $S'_1(1, \lambda)$ 的零点. 则将 $\lambda = \xi_n$ 和 $\lambda = \eta_n$ 代入(4.8) 式容易得到

$\int^{1}_{0}\!\!w_1(t)\frac{\sin\sqrt{\xi_n} t}{\sqrt{\xi_n}}{\rm d}t = 0 \ (n\in{\Bbb N}), \; \; \; \; \int^{1}_{0}\!\!w_2(t)\cos\sqrt{\eta_n}{\rm d}t = 0 \ (n\in{\Bbb N}\cup\{0\}).$

而又因为 $\{\frac{\sin\sqrt{\xi_n} t}{\sqrt{\xi_n}}\}_{n\in{\Bbb N}}$ 和 $\{\cos\sqrt{\eta_n}t\}_{n\in{\Bbb N}\cup\{0\}}$ 在 $L_2(0, 1)$ 里完备^[5], 所以 $w_1 = 0$ , $w_2 = 0$ , 因此 $V$ 在 $H$ 中完备.

下面基于引理4.1证明反问题解的唯一性. 首先定义在边值问题 $L$ 的基础上, 考虑同样形式的问题 $\widetilde{L}$ , 但有不同的势函数 $q$ , 如果有某个符号 $\gamma$ 表示与 $L$ 相关的对象, 则对应的符号 $\widetilde{\gamma}$ 表示与 $\widetilde{L}$ 相关的类似对象.

定理4.2 设边值问题 $L$ 和 $\widetilde{L}$ 及其子谱 $\Lambda$ 和 $\widetilde{\Lambda}$ 定义如上, 且满足假设(1)–(3), $q_2(x) = \widetilde{q}_2(x),$ $x\in(0, 2); q_3(x) = \widetilde{q}_3(x), x\in(0, 3)$ , 以及 $\Lambda = \widetilde{\Lambda}$ , 则在 $(0, 1)$ 上有 $q_1(x) = \widetilde{q}_1(x)$ .

证因为 $q_2(x) = \widetilde{q}_2(x)$ , $q_3(x) = \widetilde{q}_3(x)$ , 得到 $S_2(2, \lambda)\equiv\widetilde{S}_2(2, \lambda), S'_2(2, \lambda)\equiv\widetilde{S}'_2(2, \lambda),$ $S_3(3, \lambda)\equiv\widetilde{S}_3(3, \lambda), S'_3(3, \lambda)\equiv\widetilde{S}'_3(3, \lambda)$ . 再由(3.11)式和 $\Lambda = \widetilde{\Lambda}$ , 观察到 $v_{nj} = \widetilde{v}_{nj}$ ; $f_{nj} = \widetilde{f}_{nj}$ , $(n, j)\in{\cal I}$ . 而由引理3.2又知系 $V$ 在 $H$ 中完备, 因此由(3.13)式可知 $S_1(1, \lambda)\equiv\widetilde{S}_1(1, \lambda)$ , $S'_1(1, \lambda)\equiv\widetilde{S}'_1(1, \lambda)$ . 所以由文献[6]得到在 $(0, 1)$ 上, 有 $q_1(x) = \widetilde{q}_1(x)$ .

5 部分反问题重构算法

引理5.1 向量函数系 $V = \{v_{nj}\}_{(n, j)\in{\cal I}}$ 在 $H$ 中是Riese基.

证由(2.5)和(4.3)式, 有

$a_{nj} = 2\sin2\rho_{nj}(1-\cos3\rho_{nj})-\cos2\rho_{nj}\sin3\rho_{nj}+\kappa_n,$

$b_{nj} = -\sin2\rho_{nj}\sin3\rho_{nj}+\kappa_n, \ \ \ \ (n, j)\in{\cal I}.$

因此我们有 $\{||v_{nj}-v^{0}_{nj}||_{{\cal H}}\}_{(n, j)\in{\cal I}}\in l_2$ , 其中

$\begin{eqnarray*} v^{0}_{nk}(t) = \left[ \begin{array}{c} [2\sin2\alpha_k(1-\cos3\alpha_k)-\cos2\alpha_k\sin3\alpha_k] \sin|2\pi n+\alpha_k|t\\ -\sin2\alpha_k\sin3\alpha_k\cos|2\pi n+\alpha_k|t \end{array} \right]. \end{eqnarray*}$

注意到由(3.2)式可以看出 $2\sin2\alpha_k(1-\cos3\alpha_k)-\cos2\alpha_k\sin3\alpha_k\neq0, \sin2\alpha_k\sin3\alpha_k \neq0$ . 下证函数系 $V^0: = \{v^{0}_{nj}\}_{(n, j)\in{\cal I}}$ 在 $H$ 中是Riesz基. 易知 $\{\sin(2\pi n+\alpha_1)t \}_{n\in{\Bbb Z}}$ , $\{\cos(2\pi n+\alpha_2)t\}_{n\in{\Bbb Z}}$ 是 $L_2(0, 1)$ 中的Riese基. 引入线性算子A, B: ${\cal H}\rightarrow {\cal H}$ $v\in{\cal H}$ , 满足

$Av = A\left[ \begin{array}{c} v_1\\ v_2 \end{array} \right] = \left[ \begin{array}{c} v_1\\ { } v_2+\frac{\sin2\alpha_1\sin3\alpha_1}{2\sin2\alpha_1(1-\cos3\alpha_1)-\cos2\alpha_1\sin3\alpha_1}f(v_1) \end{array} \right],$

$Bv = B\left[ \begin{array}{c} v_1\\ v_2 \end{array} \right] = \left[ \begin{array}{c} { } v_1+\frac{2\sin2\alpha_2(1-\cos3\alpha_2)-\cos2\alpha_2\sin3\alpha_2}{\sin2\alpha_2\sin3\alpha_2}g(v_2)\\ v_2 \end{array} \right],$

其中

$f(u_1)(t) = \sum\limits_{n\in{\Bbb Z}}c_{n}(u_1)\cos|2\pi n+\alpha_1|t,$

$u_1(t) = \sum \limits_{n\in{\Bbb Z}}c_{n}(u_1)\sin|2\pi n+\alpha_1|t,$

$g(u_2)(t) = \sum\limits_{n\in{\Bbb Z}}c_{n}(u_2)\sin|2\pi n+\alpha_2|t,$

$u_2(t) = \sum \limits_{n\in{\Bbb Z}}c_{n}(u_2)\cos|2\pi n+\alpha_2|t,$

这里 $c_{n}(u_1)$ 和 $c_{n}(u_2)$ 分别是函数 $u_1, u_2$ 在Riesz基 $\{\sin|2\pi n+\alpha_1|t\}_{n\in{\Bbb {\Bbb Z}}}$ , $\{\cos(2\pi n\\+\alpha_2)t\}_{n\in{\Bbb Z}}$ 下的坐标. 从Riesz基性质可知存在正数 $C_1$ , $C_2$ 使得

$C_1||u_1||_{L_2}\leq||f(u_1)||_{L_2}\leq C_2||u_1||_{L_2},$

$C_1||u_1||_{L_2}\leq||g(u_2)||_{L_2}\leq C_2||u_1||_{L_2}.$

由此可知算子A, B及其逆

$A^{-1}v = A^{-1}\left[ \begin{array}{c} v_1\\ v_2 \end{array} \right] = \left[ \begin{array}{c} v_1\\ { } v_2-\frac{\sin2\alpha_1\sin3\alpha_1}{2\sin2\alpha_1(1-\cos3\alpha_1)-\cos2\alpha_1\sin3\alpha_1}f(v_1) \end{array} \right],$

$B^{-1}v = B^{-1}\left[ \begin{array}{c} v_1\\ v_2 \end{array} \right] = \left[ \begin{array}{c} { } v_1-\frac{2\sin2\alpha_2(1-\cos3\alpha_2)-\cos2\alpha_2\sin3\alpha_2}{\sin2\alpha_2\sin3\alpha_2}g(v_2)\\ v_2 \end{array} \right]$

在 $H$ 中有界. 且算子A, B将序列 $V^0$ 映射成Riezs基

$Av^{0}_{n1}(t) = \Big(2\sin2\alpha_1(1\!-\!\cos3\alpha_1)-\!\cos2\alpha_1\sin3\alpha_1\Big)\left[ \begin{array}{c} \sin|2\pi n+\alpha_1|t \\ 0 \end{array} \right],$

$Bv^{0}_{n2}(t) = \sin2\alpha_2\sin3\alpha_2\left[ \begin{array}{c} 0 \\ \cos|2\pi n+\alpha_2|t \end{array} \right].$

即函数系 $\{Av_{n1}^0\}\bigcup \{Bv_{n2}^{0}\}$ 在 ${\cal H}$ 中是Riesz基, 因此 $V^0$ 在 ${\cal H}$ 中也是Riesz基. 又由引理3.2可知系 $V$ 在 ${\cal H}$ 中完备且和Riese基 $V^0$ 是按 $l_2$ 逼近, 因此 $V$ 在 ${\cal H}$ 中是Riezs基.

重构算法: 给定函数 $q_2, q_3$ , 和特征值 $\Lambda$ .

步骤1 解初值问题

$l_jS_j(x_j, \lambda_{nj}) = \lambda_{nj} S_j(x_j, \lambda_{nj}), S_j(0, \lambda_{nj}) = 0, S'_j(0, \lambda_{nj}) = 1,$

$l_jC_j(x_j, \lambda_{nj}) = \lambda_{nj} C_j(x_j, \lambda_{nj}), C_j(0, \lambda_{nj}) = 1, C'_j(0, \lambda_{nj}) = 0, {\nonumber} j = 2, 3.$

构造函数 $S_1(1, \lambda_{nj}), S'_1(1, \lambda_{nj})$ , $S_2(1, \lambda_{nj}), S'_2(1, \lambda_{nj})$ , 其中 $(n, j)\in{\cal I}$ .

步骤2 通过(4.2)和(4.5)式得到向量函数 $v_{nj}$ , $f_{nj}$ .

步骤3 构造向量函数 $f$ , 通过它在Riesz基上的坐标, 即构造 $K(t)$ , $N(t)$ .

步骤4 由(4.1)式计算得到 $S_1(1, \rho)$ , $S'_1(1, \rho)$ .

步骤5 参考文献[4], 由Weyl函数重构函数 $q_1$ .

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Belishev

M I

Boundary spectral inverse problem on a class of graphs (trees) by the BC-method

Inverse Problems, 2004, 20 (3): 647- 672

DOI:10.1088/0266-5611/20/3/002 [本文引用: 1]

[2]

Bondarenko

N P

A partial inverse problem for the Sturm-Liouville operator on a star-shaped graph

Analysis and Mathematical Physics, 2018, 8 (1): 155- 168

DOI:10.1007/s13324-017-0172-x [本文引用: 1]

[3]

Bondarenko

N P

, Shieh

C T

Partial inverse problems for quadratic differential pencils on a graph with a loop

Journal of Inverse and Ill-Posed Problems, 2020, 28 (3): 449- 463

DOI:10.1515/jiip-2018-0104 [本文引用: 1]

[4]

Freiling

, Yurko

V A

Inverse Sturm-Liouville Problems and Their Applications. New York: Nova Science Publishers, 2001

[本文引用: 3]

[5]

, Volkmer

Riesz bases of solutions of Sturm-Liouville equations

Journal of Fourier Analysis and Applications, 2001, 7 (3): 297- 307

DOI:10.1007/BF02511815 [本文引用: 1]

[6]

Kuchment

Quantum graphs: I. Some basic structures

Waves in Random Media, 2004, 14 (1): S107- S128

DOI:10.1088/0959-7174/14/1/014 [本文引用: 2]

[7]

Kurasov

, Nowaczyk

Inverse spectral problem for quantum graphs

Journal of Physics A: Mathematical and General, 2005, 38 (22): 4901- 4915

DOI:10.1088/0305-4470/38/22/014 [本文引用: 1]

[8]

Wang

Y P

, Shieh

C T

Inverse problems for Sturm-Liouville operators on a star-shaped graph with mixed spectral data

Applicable Analysis, 2019, 99 (14): 2371- 2380

URL [本文引用: 1]

[9]

Yang

C F

Inverse spectral problems for the Sturm-Liouville operator on a d-star graph

Journal of Mathematical Analysis and Applications, 2010, 365 (2): 742- 749

DOI:10.1016/j.jmaa.2009.12.016 [本文引用: 1]

[10]

Yang

C F

, Bondarenko

N P

A partial inverse problem for the Sturm-Liouville operator on the lasso-graph

Inverse Problems and Imaging, 2018, 13 (1): 69- 79

URL [本文引用: 1]

[11]

Yurko

V A

Inverse spectral problems for Sturm-Liouville operators on graphs

Inverse Problems, 2005, 21 (3): 1075- 1086

DOI:10.1088/0266-5611/21/3/017 [本文引用: 1]

[12]

Yurko

V A

Inverse spectral problems for differential operators on arbitrary compact graphs

Journal of Inverse and Ill-Posed Problems, 2010, 18 (3): 245- 261

URL [本文引用: 1]

Boundary spectral inverse problem on a class of graphs (trees) by the BC-method

2004

... 量子图上微分算子是现代数学物理研究的一个重要方向. 该模型的重要性出现在碳纳米结构、声学和光子晶体理论研究中^{[1, 6-7, 11-12]}. 本文主要是构造量子图上Sturm-Liouville算子中的未知势函数. 这个问题在星型图上已经解决^{[2, 8-9]}. 本文考虑带环量子图：在假定两条边上的势函数是已知的情况下去重构剩余未知势函数. 杨和Bondarenko^[10]考虑了带有一个环的套索图. 在此基础上, Bodarenko和Shieh又研究了具有一个环和

$n-1$

条边的量子图, 利用Riesz基和Weyl函数得到了部分反问题的唯一性定理和构造解^[3]. ...

A partial inverse problem for the Sturm-Liouville operator on a star-shaped graph

2018

$n-1$

条边的量子图, 利用Riesz基和Weyl函数得到了部分反问题的唯一性定理和构造解^[3]. ...

Partial inverse problems for quadratic differential pencils on a graph with a loop

2020

$n-1$

条边的量子图, 利用Riesz基和Weyl函数得到了部分反问题的唯一性定理和构造解^[3]. ...

2001

... 记

$C_j(x_j, \lambda), S(x_j, \lambda)$

为等式(2.1) 满足初值条件:

$C_j(0, \lambda) = S'_j(0, \lambda) = 1,$

$C'_j(0, \lambda) = \\S_j(0, \lambda) = 0$

下的解, 则由文献[4]得到如下关系式 ...

... 下面我们考虑它的零点的分布情况, 基于儒歇定理([4], 定理1.1.3)及渐近分析有如下引理. ...

... 步骤5 参考文献[4], 由Weyl函数重构函数

$q_1$

. ...

Riesz bases of solutions of Sturm-Liouville equations

2001

... 而又因为

$\{\frac{\sin\sqrt{\xi_n} t}{\sqrt{\xi_n}}\}_{n\in{\Bbb N}}$

和

$\{\cos\sqrt{\eta_n}t\}_{n\in{\Bbb N}\cup\{0\}}$

在

$L_2(0, 1)$

里完备^[5], 所以

$w_1 = 0$

$w_2 = 0$

, 因此

$V$

在

$H$

中完备. ...

Quantum graphs: I. Some basic structures

2004

$n-1$

条边的量子图, 利用Riesz基和Weyl函数得到了部分反问题的唯一性定理和构造解^[3]. ...

... 证因为

$q_2(x) = \widetilde{q}_2(x)$

$q_3(x) = \widetilde{q}_3(x)$

, 得到

$S_2(2, \lambda)\equiv\widetilde{S}_2(2, \lambda), S'_2(2, \lambda)\equiv\widetilde{S}'_2(2, \lambda),$

$S_3(3, \lambda)\equiv\widetilde{S}_3(3, \lambda), S'_3(3, \lambda)\equiv\widetilde{S}'_3(3, \lambda)$

. 再由(3.11)式和

$\Lambda = \widetilde{\Lambda}$

, 观察到

$v_{nj} = \widetilde{v}_{nj}$

;

$f_{nj} = \widetilde{f}_{nj}$

$(n, j)\in{\cal I}$

. 而由引理3.2又知系

$V$

在

$H$

中完备, 因此由(3.13)式可知

$S_1(1, \lambda)\equiv\widetilde{S}_1(1, \lambda)$

$S'_1(1, \lambda)\equiv\widetilde{S}'_1(1, \lambda)$

. 所以由文献[6]得到在

$(0, 1)$

上, 有

$q_1(x) = \widetilde{q}_1(x)$

. ...

Inverse spectral problem for quantum graphs

2005

$n-1$

条边的量子图, 利用Riesz基和Weyl函数得到了部分反问题的唯一性定理和构造解^[3]. ...

Inverse problems for Sturm-Liouville operators on a star-shaped graph with mixed spectral data

2019

$n-1$

条边的量子图, 利用Riesz基和Weyl函数得到了部分反问题的唯一性定理和构造解^[3]. ...

Inverse spectral problems for the Sturm-Liouville operator on a d-star graph

2010

$n-1$

条边的量子图, 利用Riesz基和Weyl函数得到了部分反问题的唯一性定理和构造解^[3]. ...

A partial inverse problem for the Sturm-Liouville operator on the lasso-graph

2018

$n-1$

条边的量子图, 利用Riesz基和Weyl函数得到了部分反问题的唯一性定理和构造解^[3]. ...

Inverse spectral problems for Sturm-Liouville operators on graphs

2005

$n-1$

条边的量子图, 利用Riesz基和Weyl函数得到了部分反问题的唯一性定理和构造解^[3]. ...

Inverse spectral problems for differential operators on arbitrary compact graphs

2010

$n-1$

条边的量子图, 利用Riesz基和Weyl函数得到了部分反问题的唯一性定理和构造解^[3]. ...

〈

〉