1 引言
流体模型是一个输入-输出系统, 其中流体连续地流入和流出一个缓冲器, 其流入率和流出率由一个外部随机过程(或称驱动系统)控制.在这个信息技术高速发展的时代, 传统的离散时间排队模型有很大的局限性, 流体模型已经成为通信网络和计算机技术性能评价的重要指标, 并受到众多学者的关注.
Virtamo和Norro[1]对M/M/1队列驱动的流体模型进行了研究, 推广了有限状态环境使用的谱分析方法, 并且使用第二类切比雪夫多项式给出库存量平稳分布. Parthasarathy, Vijayashree和Lenin[2]运用了连分数法给出了由M/M/1队列驱动的流体队列缓冲器占用率和缓冲器容量的平稳分布的完整解. Adan和Resing[3]运用嵌入时间点的方法分析了有M/M/1驱动的流体模型, 并根据第一类修正的Bessel函数表示出了其库存量的平稳分布. Sericoal, Parthasarathy和Vijayashree[4]使用连续分数法明确地获得了由M/M/1排队驱动的流体模型的瞬态解, 并说明了缓冲器在指定时间为空的概率.
如果把网络中多个信息节点看作一个多服务台的排队系统, 节点中的信息流看作流体, 信道相当于流体模型的缓冲器.当信道没有收到干扰, 信息节点正常传输, 系统处于忙期; 当信道收到干扰时, 信息节点传输速率降低, 相当于系统处于工作休假期; 当信道未受干扰时, 但信息节点中无信息传输时, 系统处于闲期.在此基础上, 本文构建了单重工作休假M/M/c排队系统驱动的流体模型, 研究系统的性能指标, 并将其应用到无线Mesh网络中, 分析参数变化对系统性能的影响.
2 驱动系统的基本描述
在驱动系统中, 假设顾客的到达时间间隔和正规忙期的服务时间分别服从参数为
假设到达时间间隔、服务时间和工作休假时间之间相互独立.另外, 采用先到先服务(FCFS)的排队规则.
设
则
其中
引理2.1[8] 如果系统负载
其中r =
系统负载
可以得到如下定理.
定理2.1 若
其中
证 记π0
由xB[R] = 0, 可以得到方程组
方程组各式依次定义为(2.4.1)–(2.4.7).
从(2.4.1)式可以得到
把(2.5)式代入(2.4.4)式中递推得到
根据(2.4.7)式, 可以得到
结合(2.6)式和(2.4.5)式, 得
根据(2.4.2)式和(2.2)式, 可以得到
把(2.8)式和(2.2)式代入(2.7)式中有
另一方面, 由矩阵几何解方法知πk = πcRk-c = (πc0, πc2)Rk-c, k>c .由(2.1)式可得
进而可得(2.2)式和(2.3)式中最后一式, 其中
3 流体模型的建立与分析
3.1 流体模型的描述
用
其中
流体模型的平均漂移率为
其中
设流体模型的稳态联合分布为
则由全概率公式知, 流体模型库存量的稳态概率分布为
定理3.1
证 由
由(2.2)和(2.3)式可知
由Weierstrass判别法,
运用标准方法容易得到以下稳态联合分布
且满足边界条件为
其中概率
为了方便计算, 记向量
则微分方程组(3.1)可以写成下面的矩阵形式
其中
直接用边界条件来解矩阵方程(3.2)是非常困难的, 从而引入稳态联合分布
记
对矩阵方程(3.2)两边进行Laplace变换, 可得
利用边界条件, 整理可得
3.2 流体模型的稳态分布及均值
为了导出流体模型的稳态分布及性能指标, 引入下面两个二次方程.
引理3.1 若驱动系统的负载
易得
引理3.2 若驱动系统的负载
易得
对于任意
可以得到如下引理.
引理3.3 对于任意
这里
引理3.3的证明见文献[8].
为了得到库存量及状态的稳态联合分布函数的LT, 构造三个函数序列
可以得到如下定理.
定理3.2 若
其中
证 矩阵方程(3.3)可以写成下面的形式
方程组各式依次记为(3.11.1)
如果
首先, 对于
记
特殊地, 当
把
然后把
结合
最后通过(3.11.1)和(3.11.3)式可以得到
定理3.3
证 设
再设
又
则
从而
由级数的一致收敛性, 对于任给的
从而
于是, 当
根据极限的定义, 有
同理可知
定理3.4 当
其中
证 将(3.11.5)式从
经过移项合并之后, 得到
把(3.11.3)式代入到(3.12)式中, 可得
把(3.11.1)式和
结合定理3.3, 进而平稳分布
其中e是二维单位列向量.
由(3.4)和(3.5)式知, R(s)特征值
代入
为了得到平稳库存量的均值, 引入
易得
进而得到缓冲器库存量稳态分布的LST
根据正规化条件
进一步整理得
另一方面, 根据(3.5)式, 可以得到关系式
由
同样地, 根据(3.4)式可以得到
由
其中
众所周知
由此可得
其中
最后, 结合(3.15)和(3.16)式, 得到流体模型平稳库存量的均值表达式
其中
4 数值分析
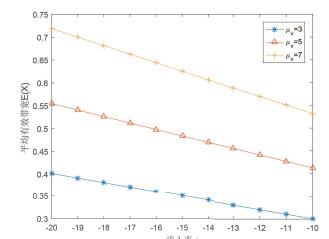
图 1
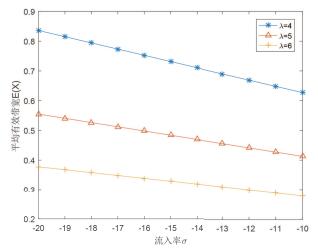
图 2
5 结论
本文讨论了一种由单重工作休假排队系统驱动的流体模型, 构建了净输入率结构, 运用LT的方法进行矩阵分析, 得到了稳态库存量的空库概率以及均值表达式, 进一步完善流体模型理论.最后将分析结果运用到多信道无线Mesh网中, 运用Matlab软件进行数值分析, 通过调节参数提高网络性能.本文所得结果为今后多服务台驱动系统的流体模型研究提供了一定的理论基础, 更好地应用到通信、交通、能源等各个领域中.
参考文献
Fluid queue driven by an M/M/1 queue
An M/M/1 driven fluid queue continued fraction approach
DOI:10.1023/A:1020157021703 [本文引用: 1]
Simple analysis of a fluid queue driven by an M/M/1 queue
Transient solution of an M/M/1 driven fluid queue
DOI:10.1080/00207160512331329041 [本文引用: 1]
Fluid model driven by an M/G/1 queue with multiple exponential vacations
DOI:10.1016/j.amc.2011.08.071 [本文引用: 1]
Analysis of fluid model modulated by an M/PH/1 working vacation queue
M/M/c排队驱动的流体模型分析
Analysis for the fluid model driven by an M/M/c queue
Stationary analysis for the fluid model driven by the M/M/c working vacation queue
一种用于多信道无线Mesh网络的信道分配方法
Channel assignment method for multi-channel wireless mesh networks
多接口多信道无线Mesh网络中面向协作通信的接口分配算法
DOI:10.3969/j.issn.1000-1220.2014.04.004 [本文引用: 1]
An interface assignment algorithm for cooperative communication in multi-interface multi-channel wireless mesh networks
DOI:10.3969/j.issn.1000-1220.2014.04.004 [本文引用: 1]
多接口多信道无线Mesh网络动态信道分配中的路由协议
DOI:10.3969/j.issn.1007-1423.2018.11.001 [本文引用: 1]
Research on routing protocol of dynamic channel allocation in multi-radio multi-channel wireless mesh network
DOI:10.3969/j.issn.1007-1423.2018.11.001 [本文引用: 1]