1 引言
进一步, 针对单个偏正态总体, Wang等[10]探讨了在变异系数和偏度参数已知时, 位置参数的区间估计问题. Gui和Guo[11]基于近似似然方程, 给出位置参数和尺度参数的显式估计. Ma等[12]在尺度参数和偏度参数已知时, 研究了位置参数的区间估计和假设检验问题.但是在实际应用中, 对多个偏正态总体的共同位置参数进行研究是无法回避的.例如, 在可靠性和寿命测试的层面中, 对多个偏正态总体的共同位置参数研究就等同于对共同保修期限的估计.然而, 目前对共同位置参数的研究主要集中在高斯分布、逆高斯分布、对数正态分布以及指数分布中[13-22].但实际数据更符合偏正态分布特征.鉴于此, 本文针对多个尺度参数和偏度参数未知的偏正态总体, 基于Bootstrap方法构造其共同位置参数的置信区间.
本文安排如下.第2小节针对多个偏正态总体, 分别给出未知参数的矩估计和极大似然估计.第3小节将徐礼文[1]对多个正态总体共同均值的探讨推广到多个偏正态总体, 进而构造共同位置参数的Bootstrap置信区间和Bootstrap检验统计量.第4小节给出上述方法的Monte Carlo模拟结果, 以验证上述方法的统计优良性.第5小节将本文所给方法应用于中国区域生产总值和生物利用度数据的案例分析.第6小节给出本文小结.第4小节中的模拟结果在附录7中.
2 多个总体的参数估计
首先, 本小节考虑单个偏正态总体参数的估计问题.设
定理2.1 设
其中
证 令
易见,
则由(2.4)式可得
根据(2.3)和(2.5)式, 可得
其中
其中
令
定理2.2 设
证 首先, 对
则
由(2.6)和(2.7)式可得
由于
定理2.2证毕.
注2.1 由(2.2)式可知, 若偏度参数
下面进一步考虑中心化参数
由(2.9)式可得对数似然函数为
于是, 令
进一步, 可得
由(2.6)式可得直接参数
则
定理2.3 令
其中,
现将一个偏正态总体拓展至多个具有共同位置参数且相互独立的偏正态总体.设
类似于一个总体的情况, 我们考虑多个偏正态总体中未知参数
其中
若
借鉴Graybill-Deal估计的思想[26], 可得
其中
其中
其中
3 Bootstrap置信区间和Bootstrap检验
本小节利用Bootstrap方法探讨共同位置参数
众所周知, 当
然而, 在实际问题中
显然, 枢轴量
令
进而, 类似于(3.2)和(3.3)式, 分别构造Bootstrap枢轴量
令
同理可得基于
进一步, 我们考虑共同位置参数
其中
若
类似于
分别基于
其中,
注3.2 当
此外, 本文基于不同权重给出第二种Bootstrap置信区间.令
分别将
类似于
令
同理可得, 基于
在假设检验问题(3.9)成立的条件下, 类似于(3.14)式构造检验统计量为
类似于
同样地,
4 Monte Carlo模拟
本小节通过Monte Carlo模拟, 从数值上研究上述置信区间的覆盖概率和区间长度的统计性质.为方便起见, 本小节针对共同位置参数
Step 1 对于给定的
Step 2 由(2.15)和(2.17)式, 可得
Step 3 生成Bootstrap样本
Step 4 由(2.15)式, 利用Bootstrap样本计算矩估计值
Step 5 将步骤3和步骤4重复
Step 6 将步骤1和步骤5重复
在模拟研究中, 令名义置信水平为95%, 内循环数
对于三个总体, 设尺度参数
对于五个总体, 设尺度参数
类似于第3节中给出的方法, 我们在模拟中增加两种基于惩罚极大似然方法的Bootstrap置信区间[27], 分别记作
对于两个总体, 表 1和表 4分别给出六种Bootstrap置信区间的模拟覆盖概率和区间长度.就覆盖概率而言, 当偏度参数较小时,
表 1 两个总体时六种Bootstrap置信区间的模拟覆盖概率
| (λ1, λ2) = (3, 4) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.8616 | 0.8552 | 0.8740 | 0.9488 | 0.9532 | 0.9460 | 0.9012 | 0.8984 | 0.8980 | 0.9500 | 0.9540 | 0.9548 | ||
| 0.8636 | 0.8564 | 0.8748 | 0.9492 | 0.9528 | 0.9464 | 0.9008 | 0.8968 | 0.8980 | 0.9508 | 0.9536 | 0.9548 | ||
| 0.8636 | 0.8564 | 0.8752 | 0.9492 | 0.9524 | 0.9472 | 0.9012 | 0.8948 | 0.8988 | 0.9508 | 0.9536 | 0.9548 | ||
| 0.8616 | 0.8552 | 0.8740 | 0.9488 | 0.9532 | 0.9460 | 0.9012 | 0.8984 | 0.8980 | 0.9500 | 0.9540 | 0.9548 | ||
| 0.8612 | 0.8552 | 0.8736 | 0.9484 | 0.9532 | 0.9460 | 0.9008 | 0.9000 | 0.8980 | 0.9500 | 0.9548 | 0.9536 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9388 | 0.9224 | 0.9248 | 0.9464 | 0.9544 | 0.9588 | 0.9260 | 0.9324 | 0.9396 | 0.9492 | 0.9544 | 0.9532 | ||
| 0.9392 | 0.9196 | 0.9256 | 0.9464 | 0.9536 | 0.9600 | 0.9260 | 0.9292 | 0.9400 | 0.9492 | 0.9532 | 0.9532 | ||
| 0.9396 | 0.9196 | 0.9260 | 0.9464 | 0.9536 | 0.9600 | 0.9260 | 0.9284 | 0.9404 | 0.9488 | 0.9528 | 0.9532 | ||
| 0.9388 | 0.9224 | 0.9248 | 0.9464 | 0.9544 | 0.9588 | 0.9260 | 0.9324 | 0.9396 | 0.9492 | 0.9544 | 0.9532 | ||
| 0.9388 | 0.9224 | 0.9252 | 0.9464 | 0.9548 | 0.9588 | 0.9260 | 0.9332 | 0.9396 | 0.9492 | 0.9544 | 0.9532 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9236 | 0.9376 | 0.9404 | 0.9412 | 0.9492 | 0.9520 | 0.9284 | 0.9336 | 0.9400 | 0.9472 | 0.9536 | 0.9576 | ||
| 0.9240 | 0.9348 | 0.9404 | 0.9408 | 0.9472 | 0.9512 | 0.9288 | 0.9300 | 0.9408 | 0.9468 | 0.9536 | 0.9576 | ||
| 0.9244 | 0.9336 | 0.9404 | 0.9408 | 0.9472 | 0.9512 | 0.9288 | 0.9292 | 0.9408 | 0.9472 | 0.9528 | 0.9576 | ||
| 0.9236 | 0.9376 | 0.9404 | 0.9412 | 0.9492 | 0.9520 | 0.9284 | 0.9336 | 0.9400 | 0.9472 | 0.9536 | 0.9576 | ||
| 0.9228 | 0.9392 | 0.9404 | 0.9412 | 0.9496 | 0.9520 | 0.9284 | 0.9348 | 0.9400 | 0.9472 | 0.9540 | 0.9576 | ||
| (λ1, λ2) = (5, 6) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9312 | 0.9312 | 0.9400 | 0.9652 | 0.9688 | 0.9656 | 0.9548 | 0.9532 | 0.9584 | 0.9656 | 0.9684 | 0.9724 | ||
| 0.9320 | 0.9312 | 0.9408 | 0.9652 | 0.9688 | 0.9660 | 0.9556 | 0.9504 | 0.9592 | 0.9656 | 0.9680 | 0.9724 | ||
| 0.9328 | 0.9304 | 0.9408 | 0.9652 | 0.9688 | 0.9660 | 0.9556 | 0.9496 | 0.9596 | 0.9656 | 0.9680 | 0.9728 | ||
| 0.9312 | 0.9312 | 0.9400 | 0.9652 | 0.9688 | 0.9656 | 0.9548 | 0.9532 | 0.9584 | 0.9656 | 0.9684 | 0.9724 | ||
| 0.9312 | 0.9324 | 0.9400 | 0.9652 | 0.9688 | 0.9656 | 0.9548 | 0.9536 | 0.9580 | 0.9660 | 0.9684 | 0.9720 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9680 | 0.9572 | 0.9660 | 0.9612 | 0.9652 | 0.9724 | 0.9584 | 0.9584 | 0.9680 | 0.9648 | 0.9696 | 0.9716 | ||
| 0.9680 | 0.9548 | 0.9660 | 0.9620 | 0.9640 | 0.9724 | 0.9588 | 0.9552 | 0.9680 | 0.9648 | 0.9684 | 0.9716 | ||
| 0.9676 | 0.9544 | 0.9664 | 0.9616 | 0.9640 | 0.9724 | 0.9588 | 0.9544 | 0.9680 | 0.9648 | 0.9684 | 0.9716 | ||
| 0.9680 | 0.9572 | 0.9660 | 0.9612 | 0.9652 | 0.9724 | 0.9584 | 0.9584 | 0.9680 | 0.9648 | 0.9696 | 0.9716 | ||
| 0.9676 | 0.9592 | 0.9656 | 0.9612 | 0.9652 | 0.9728 | 0.9576 | 0.9588 | 0.9680 | 0.9648 | 0.9704 | 0.9716 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9532 | 0.9668 | 0.9680 | 0.9620 | 0.9676 | 0.9724 | 0.9564 | 0.9560 | 0.9668 | 0.9588 | 0.9708 | 0.9692 | ||
| 0.9524 | 0.9640 | 0.9680 | 0.9616 | 0.9672 | 0.9724 | 0.9568 | 0.9524 | 0.9664 | 0.9588 | 0.9688 | 0.9692 | ||
| 0.9524 | 0.9636 | 0.9680 | 0.9616 | 0.9672 | 0.9728 | 0.9564 | 0.9520 | 0.9668 | 0.9588 | 0.9680 | 0.9692 | ||
| 0.9532 | 0.9668 | 0.9680 | 0.9620 | 0.9676 | 0.9724 | 0.9564 | 0.9560 | 0.9668 | 0.9588 | 0.9708 | 0.9692 | ||
| 0.9536 | 0.9672 | 0.9676 | 0.9620 | 0.9684 | 0.9720 | 0.9564 | 0.9580 | 0.9672 | 0.9588 | 0.9716 | 0.9692 | ||
| (λ1, λ2) = (8, 9) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9548 | 0.9564 | 0.9620 | 0.9736 | 0.9752 | 0.9720 | 0.9680 | 0.9664 | 0.9720 | 0.9724 | 0.9744 | 0.9776 | ||
| 0.9548 | 0.9556 | 0.9628 | 0.9736 | 0.9752 | 0.9716 | 0.9684 | 0.9656 | 0.9728 | 0.9724 | 0.9744 | 0.9776 | ||
| 0.9548 | 0.9552 | 0.9628 | 0.9736 | 0.9752 | 0.9716 | 0.9684 | 0.9656 | 0.9736 | 0.9724 | 0.9744 | 0.9780 | ||
| 0.9548 | 0.9564 | 0.9620 | 0.9736 | 0.9752 | 0.9720 | 0.9680 | 0.9664 | 0.9720 | 0.9724 | 0.9744 | 0.9776 | ||
| 0.9548 | 0.9576 | 0.9624 | 0.9736 | 0.9756 | 0.9720 | 0.9680 | 0.9664 | 0.9720 | 0.9724 | 0.9748 | 0.9776 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9764 | 0.9676 | 0.9764 | 0.9668 | 0.9708 | 0.9776 | 0.9716 | 0.9680 | 0.9772 | 0.9704 | 0.9764 | 0.9796 | ||
| 0.9764 | 0.9660 | 0.9764 | 0.9672 | 0.9704 | 0.9772 | 0.9720 | 0.9648 | 0.9776 | 0.9700 | 0.9756 | 0.9800 | ||
| 0.9764 | 0.9656 | 0.9764 | 0.9672 | 0.9704 | 0.9772 | 0.9716 | 0.9640 | 0.9776 | 0.9700 | 0.9752 | 0.9800 | ||
| 0.9764 | 0.9676 | 0.9764 | 0.9668 | 0.9708 | 0.9776 | 0.9716 | 0.9680 | 0.9772 | 0.9704 | 0.9764 | 0.9796 | ||
| 0.9760 | 0.9684 | 0.9764 | 0.9668 | 0.9716 | 0.9776 | 0.9704 | 0.9696 | 0.9772 | 0.9704 | 0.9768 | 0.9796 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9692 | 0.9748 | 0.9780 | 0.9704 | 0.9748 | 0.9772 | 0.9692 | 0.9772 | 0.9836 | 0.9684 | 0.9788 | 0.9736 | ||
| 0.9696 | 0.9732 | 0.9784 | 0.9700 | 0.9736 | 0.9772 | 0.9656 | 0.9760 | 0.9876 | 0.9680 | 0.9768 | 0.9736 | ||
| 0.9696 | 0.9732 | 0.9784 | 0.9704 | 0.9736 | 0.9772 | 0.9656 | 0.9764 | 0.9809 | 0.9680 | 0.9768 | 0.9736 | ||
| 0.9692 | 0.9748 | 0.9780 | 0.9704 | 0.9748 | 0.9772 | 0.9692 | 0.9772 | 0.9863 | 0.9684 | 0.9788 | 0.9736 | ||
| 0.9696 | 0.9756 | 0.9784 | 0.9704 | 0.9756 | 0.9772 | 0.9700 | 0.9772 | 0.9868 | 0.9684 | 0.9800 | 0.9732 | ||
注:
表 2 三个总体时六种Bootstrap置信区间的模拟覆盖概率
| (λ1, λ2, λ3) = (3, 3, 4) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.8655 | 0.8396 | 0.8668 | 0.9330 | 0.9144 | 0.9428 | 0.9085 | 0.8744 | 0.9080 | 0.9580 | 0.9388 | 0.9620 | ||
| 0.8675 | 0.8380 | 0.8668 | 0.9335 | 0.9180 | 0.9424 | 0.9080 | 0.8724 | 0.9076 | 0.9565 | 0.9432 | 0.9608 | ||
| 0.8685 | 0.8348 | 0.8668 | 0.9310 | 0.9216 | 0.9408 | 0.9065 | 0.8708 | 0.9084 | 0.9560 | 0.9480 | 0.9620 | ||
| 0.8690 | 0.8340 | 0.8672 | 0.9320 | 0.9248 | 0.9396 | 0.9080 | 0.8708 | 0.9104 | 0.9550 | 0.9492 | 0.9620 | ||
| 0.8690 | 0.8336 | 0.8676 | 0.9315 | 0.9228 | 0.9412 | 0.9060 | 0.8712 | 0.9088 | 0.9560 | 0.9484 | 0.9620 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9230 | 0.8804 | 0.9324 | 0.9580 | 0.9320 | 0.9624 | 0.9400 | 0.8988 | 0.9416 | 0.9615 | 0.9336 | 0.9664 | ||
| 0.9205 | 0.8736 | 0.9344 | 0.9570 | 0.9380 | 0.9624 | 0.9415 | 0.8976 | 0.9412 | 0.9605 | 0.9352 | 0.9664 | ||
| 0.9275 | 0.8708 | 0.9340 | 0.9560 | 0.9436 | 0.9624 | 0.9420 | 0.8964 | 0.9420 | 0.9605 | 0.9436 | 0.9676 | ||
| 0.9295 | 0.8696 | 0.9340 | 0.9545 | 0.9464 | 0.9620 | 0.9445 | 0.8944 | 0.9432 | 0.9590 | 0.9484 | 0.9672 | ||
| 0.9275 | 0.8720 | 0.9336 | 0.9560 | 0.9448 | 0.9620 | 0.9435 | 0.8964 | 0.9428 | 0.9605 | 0.9452 | 0.9672 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9415 | 0.8904 | 0.9448 | 0.9345 | 0.9000 | 0.9456 | 0.9450 | 0.8752 | 0.9420 | 0.9380 | 0.8924 | 0.9448 | ||
| 0.9430 | 0.8844 | 0.9452 | 0.9335 | 0.9088 | 0.9448 | 0.9450 | 0.8684 | 0.9420 | 0.9385 | 0.9016 | 0.9452 | ||
| 0.9450 | 0.8772 | 0.9448 | 0.9335 | 0.9200 | 0.9456 | 0.9465 | 0.8604 | 0.9424 | 0.9400 | 0.9112 | 0.9452 | ||
| 0.9440 | 0.8740 | 0.9448 | 0.9340 | 0.9252 | 0.9452 | 0.9445 | 0.8528 | 0.9424 | 0.9410 | 0.9188 | 0.9448 | ||
| 0.9445 | 0.8768 | 0.9440 | 0.9335 | 0.9228 | 0.9452 | 0.9460 | 0.8588 | 0.9424 | 0.9405 | 0.9136 | 0.9448 | ||
| (λ1, λ2, λ3) = (5, 5, 6) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9410 | 0.9036 | 0.9444 | 0.9595 | 0.9388 | 0.9664 | 0.9550 | 0.9128 | 0.9588 | 0.9670 | 0.9540 | 0.9756 | ||
| 0.9415 | 0.9004 | 0.9440 | 0.9595 | 0.9436 | 0.9664 | 0.9560 | 0.9072 | 0.9596 | 0.9665 | 0.9576 | 0.9756 | ||
| 0.9415 | 0.8936 | 0.9448 | 0.9590 | 0.9476 | 0.9656 | 0.9580 | 0.9016 | 0.9608 | 0.9670 | 0.9616 | 0.9752 | ||
| 0.9395 | 0.8892 | 0.9452 | 0.9580 | 0.9516 | 0.9644 | 0.9565 | 0.8948 | 0.9616 | 0.9670 | 0.9620 | 0.9744 | ||
| 0.9415 | 0.8920 | 0.9444 | 0.9590 | 0.9484 | 0.9652 | 0.9575 | 0.9016 | 0.9612 | 0.9670 | 0.9616 | 0.9752 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9630 | 0.8964 | 0.9704 | 0.9735 | 0.9432 | 0.9796 | 0.9650 | 0.8976 | 0.9704 | 0.9735 | 0.9444 | 0.9796 | ||
| 0.9635 | 0.8852 | 0.9704 | 0.9725 | 0.9492 | 0.9800 | 0.9655 | 0.8904 | 0.9688 | 0.9740 | 0.9516 | 0.9796 | ||
| 0.9650 | 0.8672 | 0.9704 | 0.9730 | 0.9576 | 0.9804 | 0.9655 | 0.8760 | 0.9696 | 0.9745 | 0.9588 | 0.9792 | ||
| 0.9625 | 0.8608 | 0.9692 | 0.9720 | 0.9620 | 0.9800 | 0.9650 | 0.8660 | 0.9708 | 0.9745 | 0.9628 | 0.9784 | ||
| 0.9645 | 0.8652 | 0.9692 | 0.9730 | 0.9604 | 0.9800 | 0.9650 | 0.8744 | 0.9692 | 0.9745 | 0.9604 | 0.9788 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9665 | 0.8680 | 0.9716 | 0.9520 | 0.9200 | 0.9696 | 0.9595 | 0.8388 | 0.9672 | 0.9595 | 0.9060 | 0.9660 | ||
| 0.9650 | 0.8536 | 0.9724 | 0.9510 | 0.9292 | 0.9696 | 0.9595 | 0.8196 | 0.9688 | 0.9585 | 0.9192 | 0.9660 | ||
| 0.9650 | 0.8336 | 0.9712 | 0.9515 | 0.9364 | 0.9688 | 0.9620 | 0.7944 | 0.9688 | 0.9585 | 0.9312 | 0.9656 | ||
| 0.9660 | 0.8248 | 0.9688 | 0.9520 | 0.9404 | 0.9688 | 0.9625 | 0.7784 | 0.9676 | 0.9585 | 0.9380 | 0.9668 | ||
| 0.9655 | 0.8312 | 0.9700 | 0.9520 | 0.9380 | 0.9692 | 0.9620 | 0.7900 | 0.9684 | 0.9585 | 0.9320 | 0.9664 | ||
| (λ1, λ2, λ3) = (6, 8, 9) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9510 | 0.9116 | 0.9568 | 0.9650 | 0.9484 | 0.9728 | 0.9625 | 0.9184 | 0.9656 | 0.9765 | 0.9620 | 0.9816 | ||
| 0.9510 | 0.9104 | 0.9560 | 0.9650 | 0.9524 | 0.9732 | 0.9620 | 0.9108 | 0.9656 | 0.9755 | 0.9628 | 0.9812 | ||
| 0.9525 | 0.9016 | 0.9552 | 0.9650 | 0.9572 | 0.9728 | 0.9640 | 0.9060 | 0.9660 | 0.9735 | 0.9660 | 0.9816 | ||
| 0.9510 | 0.8952 | 0.9548 | 0.9655 | 0.9612 | 0.9724 | 0.9640 | 0.9000 | 0.9664 | 0.9730 | 0.9684 | 0.9800 | ||
| 0.9530 | 0.9008 | 0.9548 | 0.9650 | 0.9588 | 0.9728 | 0.9645 | 0.9048 | 0.9664 | 0.9730 | 0.9660 | 0.9816 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9685 | 0.8964 | 0.9748 | 0.9780 | 0.9568 | 0.9820 | 0.9705 | 0.9036 | 0.9744 | 0.9785 | 0.9560 | 0.9828 | ||
| 0.9695 | 0.8868 | 0.9756 | 0.9785 | 0.9604 | 0.9824 | 0.9705 | 0.8928 | 0.9740 | 0.9785 | 0.9616 | 0.9824 | ||
| 0.9695 | 0.8660 | 0.9756 | 0.9775 | 0.9672 | 0.9820 | 0.9705 | 0.8744 | 0.9744 | 0.9780 | 0.9664 | 0.9824 | ||
| 0.9695 | 0.8560 | 0.9760 | 0.9775 | 0.9704 | 0.9820 | 0.9695 | 0.8652 | 0.9756 | 0.9780 | 0.9704 | 0.9824 | ||
| 0.9695 | 0.8644 | 0.9756 | 0.9775 | 0.9668 | 0.9820 | 0.9705 | 0.8728 | 0.9740 | 0.9780 | 0.9672 | 0.9828 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9720 | 0.8676 | 0.9776 | 0.9630 | 0.9324 | 0.9768 | 0.9665 | 0.8388 | 0.9736 | 0.9690 | 0.9224 | 0.9716 | ||
| 0.9715 | 0.8516 | 0.9772 | 0.9630 | 0.9372 | 0.9768 | 0.9660 | 0.8068 | 0.9744 | 0.9690 | 0.9320 | 0.9708 | ||
| 0.9705 | 0.8300 | 0.9776 | 0.9610 | 0.9468 | 0.9764 | 0.9680 | 0.7800 | 0.9732 | 0.9695 | 0.9428 | 0.9708 | ||
| 0.9700 | 0.8156 | 0.9752 | 0.9620 | 0.9520 | 0.9768 | 0.9670 | 0.7604 | 0.9724 | 0.9685 | 0.9492 | 0.9696 | ||
| 0.9700 | 0.8272 | 0.9772 | 0.9610 | 0.9476 | 0.9756 | 0.9675 | 0.7748 | 0.9728 | 0.9695 | 0.9452 | 0.9704 | ||
注:
表 3 五个总体时六种Bootstrap置信区间的模拟覆盖概率
| (λ1, λ2, λ3, λ4, λ5) = (3, 3, 4, 4, 5) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.8720 | 0.8332 | 0.8700 | 0.9600 | 0.9280 | 0.9596 | 0.9210 | 0.8760 | 0.9220 | 0.9655 | 0.9220 | 0.9664 | ||
| 0.8690 | 0.8368 | 0.8664 | 0.9545 | 0.9144 | 0.9560 | 0.9190 | 0.8836 | 0.9192 | 0.9615 | 0.9148 | 0.9656 | ||
| 0.8670 | 0.8412 | 0.8644 | 0.9500 | 0.9088 | 0.9544 | 0.9165 | 0.8868 | 0.9188 | 0.9635 | 0.9112 | 0.9660 | ||
| 0.8655 | 0.8440 | 0.8632 | 0.9525 | 0.9196 | 0.9552 | 0.9175 | 0.8900 | 0.9168 | 0.9640 | 0.9228 | 0.9648 | ||
| 0.8595 | 0.8504 | 0.8644 | 0.9500 | 0.9280 | 0.9516 | 0.9135 | 0.8948 | 0.9144 | 0.9645 | 0.9224 | 0.9636 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9300 | 0.8784 | 0.9352 | 0.9630 | 0.9132 | 0.9728 | 0.9405 | 0.8888 | 0.9400 | 0.9535 | 0.9016 | 0.9608 | ||
| 0.9290 | 0.8896 | 0.9324 | 0.9650 | 0.9056 | 0.9712 | 0.9390 | 0.8988 | 0.9388 | 0.9545 | 0.8796 | 0.9624 | ||
| 0.9270 | 0.8964 | 0.9316 | 0.9655 | 0.8936 | 0.9700 | 0.9395 | 0.9032 | 0.9396 | 0.9625 | 0.8632 | 0.9644 | ||
| 0.9260 | 0.8996 | 0.9316 | 0.9635 | 0.9152 | 0.9704 | 0.9390 | 0.9084 | 0.9376 | 0.9615 | 0.8916 | 0.9648 | ||
| 0.9240 | 0.9096 | 0.9296 | 0.9640 | 0.9164 | 0.9712 | 0.9380 | 0.9164 | 0.9344 | 0.9615 | 0.8964 | 0.9652 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9480 | 0.8772 | 0.9444 | 0.9660 | 0.9040 | 0.9672 | 0.9450 | 0.8688 | 0.9380 | 0.9630 | 0.8732 | 0.9640 | ||
| 0.9480 | 0.8844 | 0.9440 | 0.9670 | 0.8788 | 0.9700 | 0.9445 | 0.8780 | 0.9376 | 0.9580 | 0.8484 | 0.9620 | ||
| 0.9455 | 0.8976 | 0.9420 | 0.9680 | 0.8588 | 0.9692 | 0.9420 | 0.8944 | 0.9376 | 0.9565 | 0.8328 | 0.9572 | ||
| 0.9445 | 0.9048 | 0.9416 | 0.9685 | 0.8896 | 0.9692 | 0.9410 | 0.9016 | 0.9364 | 0.9565 | 0.8708 | 0.9580 | ||
| 0.9450 | 0.9152 | 0.9412 | 0.9640 | 0.8928 | 0.9684 | 0.9410 | 0.9096 | 0.9364 | 0.9590 | 0.8816 | 0.9588 | ||
| (λ1, λ2, λ3, λ4, λ5) = (4, 4, 5, 5, 6) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9250 | 0.8764 | 0.9248 | 0.9645 | 0.9248 | 0.9668 | 0.9535 | 0.8948 | 0.9568 | 0.9695 | 0.9172 | 0.9740 | ||
| 0.9235 | 0.8808 | 0.9232 | 0.9575 | 0.9096 | 0.9616 | 0.9530 | 0.9016 | 0.9552 | 0.9680 | 0.9088 | 0.9740 | ||
| 0.9220 | 0.8900 | 0.9216 | 0.9565 | 0.9012 | 0.9608 | 0.9505 | 0.9124 | 0.9532 | 0.9710 | 0.9036 | 0.9736 | ||
| 0.9195 | 0.8940 | 0.9212 | 0.9575 | 0.9144 | 0.9604 | 0.9515 | 0.9168 | 0.9516 | 0.9685 | 0.9164 | 0.9720 | ||
| 0.9160 | 0.9016 | 0.9212 | 0.9570 | 0.9188 | 0.9588 | 0.9500 | 0.9252 | 0.9516 | 0.9705 | 0.9188 | 0.9720 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9540 | 0.8812 | 0.9608 | 0.9675 | 0.9052 | 0.9756 | 0.9555 | 0.8800 | 0.9596 | 0.9620 | 0.8912 | 0.9720 | ||
| 0.9545 | 0.8968 | 0.9612 | 0.9700 | 0.8960 | 0.9780 | 0.9565 | 0.8924 | 0.9588 | 0.9580 | 0.8700 | 0.9672 | ||
| 0.9525 | 0.9076 | 0.9596 | 0.9710 | 0.8836 | 0.9764 | 0.9545 | 0.9072 | 0.9572 | 0.9645 | 0.8496 | 0.9680 | ||
| 0.9490 | 0.9140 | 0.9568 | 0.9700 | 0.9096 | 0.9772 | 0.9530 | 0.9156 | 0.9568 | 0.9640 | 0.8808 | 0.9704 | ||
| 0.9450 | 0.9288 | 0.9564 | 0.9705 | 0.9076 | 0.9772 | 0.9530 | 0.9272 | 0.9536 | 0.9650 | 0.8880 | 0.9708 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9655 | 0.8628 | 0.9640 | 0.9695 | 0.8952 | 0.9692 | 0.9545 | 0.8284 | 0.9536 | 0.9645 | 0.8544 | 0.9684 | ||
| 0.9640 | 0.8712 | 0.9632 | 0.9720 | 0.8648 | 0.9736 | 0.9540 | 0.8524 | 0.9532 | 0.9600 | 0.8264 | 0.9624 | ||
| 0.9625 | 0.8948 | 0.9632 | 0.9715 | 0.8472 | 0.9748 | 0.9535 | 0.8780 | 0.9516 | 0.9580 | 0.8032 | 0.9584 | ||
| 0.9625 | 0.9080 | 0.9620 | 0.9715 | 0.8752 | 0.9748 | 0.9530 | 0.8892 | 0.9528 | 0.9590 | 0.8532 | 0.9596 | ||
| 0.9610 | 0.9256 | 0.9608 | 0.9690 | 0.8792 | 0.9744 | 0.9515 | 0.9064 | 0.9504 | 0.9570 | 0.8632 | 0.9608 | ||
| (λ1, λ2, λ3, λ4, λ5) = (7, 7, 8, 8, 9) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9615 | 0.9072 | 0.9656 | 0.9710 | 0.9228 | 0.9756 | 0.9740 | 0.9080 | 0.9764 | 0.9770 | 0.9176 | 0.9808 | ||
| 0.9595 | 0.9152 | 0.9644 | 0.9680 | 0.9060 | 0.9712 | 0.9725 | 0.9172 | 0.9760 | 0.9760 | 0.9100 | 0.9804 | ||
| 0.9585 | 0.9236 | 0.9616 | 0.9665 | 0.8972 | 0.9684 | 0.9710 | 0.9308 | 0.9752 | 0.9765 | 0.9048 | 0.9800 | ||
| 0.9575 | 0.9308 | 0.9624 | 0.9660 | 0.9120 | 0.9692 | 0.9690 | 0.9400 | 0.9732 | 0.9770 | 0.9156 | 0.9800 | ||
| 0.9560 | 0.9372 | 0.9620 | 0.9655 | 0.9132 | 0.9700 | 0.9670 | 0.9516 | 0.9716 | 0.9755 | 0.9168 | 0.9792 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9750 | 0.8956 | 0.9800 | 0.9755 | 0.9016 | 0.9820 | 0.9735 | 0.8924 | 0.9764 | 0.9675 | 0.8852 | 0.9780 | ||
| 0.9735 | 0.9104 | 0.9792 | 0.9765 | 0.8888 | 0.9828 | 0.9735 | 0.9064 | 0.9768 | 0.9670 | 0.8664 | 0.9792 | ||
| 0.9705 | 0.9268 | 0.9796 | 0.9750 | 0.8796 | 0.9820 | 0.9725 | 0.9252 | 0.9756 | 0.9725 | 0.8432 | 0.9780 | ||
| 0.9695 | 0.9356 | 0.9800 | 0.9745 | 0.9040 | 0.9816 | 0.9715 | 0.9328 | 0.9740 | 0.9725 | 0.8752 | 0.9788 | ||
| 0.9670 | 0.9532 | 0.9780 | 0.9750 | 0.9048 | 0.9816 | 0.9695 | 0.9436 | 0.9732 | 0.9725 | 0.8796 | 0.9808 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.9780 | 0.8640 | 0.9800 | 0.9735 | 0.8916 | 0.9748 | 0.9720 | 0.8320 | 0.9764 | 0.9635 | 0.8320 | 0.9732 | ||
| 0.9775 | 0.8808 | 0.9800 | 0.9735 | 0.8584 | 0.9768 | 0.9715 | 0.8580 | 0.9756 | 0.9660 | 0.8120 | 0.9696 | ||
| 0.9770 | 0.9100 | 0.9792 | 0.9760 | 0.8352 | 0.9800 | 0.9705 | 0.8940 | 0.9748 | 0.9630 | 0.7788 | 0.9680 | ||
| 0.9760 | 0.9244 | 0.9792 | 0.9765 | 0.8652 | 0.9812 | 0.9700 | 0.9148 | 0.9736 | 0.9635 | 0.8380 | 0.9692 | ||
| 0.9760 | 0.9448 | 0.9776 | 0.9760 | 0.8648 | 0.9800 | 0.9705 | 0.9316 | 0.9728 | 0.9620 | 0.8496 | 0.9692 | ||
注:
表 4 两个总体时六种Bootstrap置信区间的模拟区间长度
| (λ1, λ2) = (3, 4) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0411 | 0.0221 | 0.0154 | 1.2987 | 1.0654 | 0.6986 | 0.0275 | 0.0201 | 0.0137 | 1.0710 | 0.9018 | 0.5738 | ||
| 0.1802 | 0.1991 | 0.1384 | 4.9169 | 6.6592 | 4.3665 | 0.1553 | 0.1808 | 0.1236 | 4.1442 | 5.6363 | 3.5863 | ||
| 0.4284 | 0.5529 | 0.3845 | 13.9794 | 17.0478 | 11.1784 | 0.4068 | 0.5022 | 0.3360 | 10.8372 | 14.4292 | 9.1810 | ||
| 0.8817 | 1.0838 | 0.7537 | 36.8349 | 52.2064 | 34.2320 | 0.8903 | 0.9845 | 0.6729 | 32.5810 | 44.1873 | 28.1151 | ||
| 1.3595 | 1.7916 | 1.2460 | 74.1995 | 106.5424 | 69.8603 | 1.4416 | 1.6275 | 1.1124 | 61.4367 | 90.1772 | 57.3771 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0252 | 0.0171 | 0.0112 | 0.8519 | 0.7178 | 0.4647 | 0.0383 | 0.0129 | 0.0083 | 0.5550 | 0.5160 | 0.3071 | ||
| 0.1485 | 0.1539 | 0.1009 | 3.2747 | 4.4861 | 2.9044 | 0.1147 | 0.1164 | 0.0746 | 2.5189 | 3.2254 | 1.9195 | ||
| 0.3626 | 0.4274 | 0.2802 | 9.6313 | 11.4847 | 7.4355 | 0.2774 | 0.3235 | 0.2072 | 6.4404 | 8.2571 | 4.9140 | ||
| 0.5683 | 0.8377 | 0.5493 | 26.9447 | 35.1702 | 22.7699 | 0.5835 | 0.6340 | 0.4062 | 21.0352 | 25.2859 | 15.0482 | ||
| 1.2108 | 1.3848 | 0.9080 | 48.5261 | 71.7750 | 46.4686 | 0.8832 | 1.0481 | 0.6715 | 32.1665 | 51.6033 | 30.7102 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0336 | 0.0110 | 0.0068 | 0.6014 | 0.3940 | 0.2379 | 0.0345 | 0.0092 | 0.0056 | 0.4908 | 0.3422 | 0.2053 | ||
| 0.0935 | 0.0986 | 0.0615 | 1.8589 | 2.4626 | 1.4867 | 0.1076 | 0.0826 | 0.0503 | 1.7424 | 2.1391 | 1.2834 | ||
| 0.2080 | 0.2740 | 0.1708 | 5.7627 | 6.3043 | 3.8061 | 0.2012 | 0.2295 | 0.1397 | 5.5726 | 5.4763 | 3.2856 | ||
| 0.4737 | 0.5371 | 0.3349 | 13.8291 | 19.3065 | 11.6555 | 0.3902 | 0.4499 | 0.2739 | 13.5280 | 16.7701 | 10.0614 | ||
| 0.8088 | 0.8878 | 0.5536 | 27.4740 | 39.4007 | 23.7863 | 0.6367 | 0.7437 | 0.4527 | 21.7438 | 34.2241 | 20.5332 | ||
| (λ1, λ2) = (5, 6) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0394 | 0.0210 | 0.0138 | 1.2360 | 1.0023 | 0.6375 | 0.0255 | 0.0183 | 0.0118 | 0.9932 | 0.8023 | 0.5009 | ||
| 0.1646 | 0.1887 | 0.1243 | 4.5252 | 6.2645 | 3.9848 | 0.1372 | 0.1645 | 0.1064 | 3.6578 | 5.0143 | 3.1310 | ||
| 0.3848 | 0.5242 | 0.3452 | 12.9767 | 16.0372 | 10.2012 | 0.3566 | 0.4568 | 0.2956 | 9.5920 | 12.8368 | 8.0154 | ||
| 0.7964 | 1.0275 | 0.6766 | 33.7643 | 49.1118 | 31.2397 | 0.7917 | 0.8955 | 0.5795 | 28.7679 | 39.3111 | 24.5460 | ||
| 1.2185 | 1.6985 | 1.1185 | 67.9331 | 100.2271 | 63.7537 | 1.2786 | 1.4804 | 0.9579 | 53.6549 | 80.2260 | 50.0932 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0228 | 0.0143 | 0.0089 | 0.7857 | 0.6215 | 0.3957 | 0.0361 | 0.0098 | 0.0061 | 0.5066 | 0.4393 | 0.2632 | ||
| 0.1275 | 0.1287 | 0.0803 | 2.8605 | 3.8848 | 2.4733 | 0.0952 | 0.0879 | 0.0545 | 2.2166 | 2.7457 | 1.6448 | ||
| 0.3042 | 0.3575 | 0.2231 | 8.5709 | 9.9451 | 6.3316 | 0.2233 | 0.2441 | 0.1515 | 5.6665 | 7.0291 | 4.2107 | ||
| 0.4537 | 0.7008 | 0.4373 | 23.6974 | 30.4554 | 19.3897 | 0.4774 | 0.4785 | 0.2969 | 18.6652 | 21.5255 | 12.8946 | ||
| 1.0214 | 1.1585 | 0.7229 | 41.8990 | 62.1532 | 39.5704 | 0.7079 | 0.7911 | 0.4908 | 27.3300 | 43.9289 | 26.3153 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0319 | 0.0080 | 0.0049 | 0.5740 | 0.3437 | 0.2114 | 0.0331 | 0.0068 | 0.0042 | 0.4703 | 0.3005 | 0.1874 | ||
| 0.0777 | 0.0724 | 0.0444 | 1.6875 | 2.1483 | 1.3215 | 0.0953 | 0.0616 | 0.0375 | 1.6146 | 1.8781 | 1.1713 | ||
| 0.1642 | 0.2010 | 0.1233 | 5.3241 | 5.4997 | 3.3830 | 0.1670 | 0.1712 | 0.1042 | 5.2454 | 4.8079 | 2.9985 | ||
| 0.3879 | 0.3939 | 0.2416 | 12.4861 | 16.8425 | 10.3598 | 0.3232 | 0.3355 | 0.2043 | 12.5257 | 14.7231 | 9.1822 | ||
| 0.6670 | 0.6512 | 0.3994 | 24.7334 | 34.3722 | 21.1422 | 0.5259 | 0.5546 | 0.3377 | 19.6984 | 30.0466 | 18.7387 | ||
| (λ1, λ2) = (8, 9) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0386 | 0.0204 | 0.0131 | 1.2039 | 0.9676 | 0.6056 | 0.0246 | 0.0174 | 0.0109 | 0.9618 | 0.7591 | 0.4681 | ||
| 0.1578 | 0.1837 | 0.1180 | 4.3248 | 6.0474 | 3.7849 | 0.1297 | 0.1563 | 0.0984 | 3.4612 | 4.7443 | 2.9255 | ||
| 0.3660 | 0.5103 | 0.3279 | 12.4635 | 15.4815 | 9.6895 | 0.3357 | 0.4342 | 0.2733 | 9.0888 | 12.1456 | 7.4894 | ||
| 0.7595 | 1.0002 | 0.6427 | 32.1929 | 47.4100 | 29.6727 | 0.7508 | 0.8511 | 0.5357 | 27.2271 | 37.1946 | 22.9350 | ||
| 1.1574 | 1.6535 | 1.0625 | 64.7261 | 96.7542 | 60.5558 | 1.2110 | 1.4069 | 0.8856 | 50.5105 | 75.9066 | 46.8056 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0219 | 0.0131 | 0.0080 | 0.7570 | 0.5777 | 0.3643 | 0.0355 | 0.0088 | 0.0054 | 0.4892 | 0.4095 | 0.2485 | ||
| 0.1190 | 0.1178 | 0.0721 | 2.6816 | 3.6109 | 2.2768 | 0.0897 | 0.0788 | 0.0486 | 2.1073 | 2.5595 | 1.5533 | ||
| 0.2806 | 0.3272 | 0.2004 | 8.1129 | 9.2440 | 5.8287 | 0.2080 | 0.2188 | 0.1351 | 5.3869 | 6.5525 | 3.9764 | ||
| 0.4076 | 0.6413 | 0.3927 | 22.2950 | 28.3083 | 17.8497 | 0.4473 | 0.4288 | 0.2648 | 17.8090 | 20.0658 | 12.1772 | ||
| 0.9453 | 1.0601 | 0.6492 | 39.0370 | 57.7713 | 36.4275 | 0.6581 | 0.7089 | 0.4378 | 25.5826 | 40.9500 | 24.8510 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0314 | 0.0072 | 0.0045 | 0.5646 | 0.3261 | 0.2034 | 0.0329 | 0.0063 | 0.0039 | 0.4632 | 0.2855 | 0.1814 | ||
| 0.0738 | 0.0651 | 0.0404 | 1.6289 | 2.0381 | 1.2713 | 0.0928 | 0.0564 | 0.0347 | 1.5702 | 1.7846 | 1.1336 | ||
| 0.1535 | 0.1809 | 0.1123 | 5.1740 | 5.2176 | 3.2545 | 0.1599 | 0.1566 | 0.0965 | 5.1318 | 4.5686 | 2.9020 | ||
| 0.3669 | 0.3546 | 0.2201 | 12.0263 | 15.9787 | 9.9664 | 0.3092 | 0.3069 | 0.1891 | 12.1779 | 13.9902 | 8.8866 | ||
| 0.6322 | 0.5862 | 0.3639 | 23.7951 | 32.6094 | 20.3393 | 0.5028 | 0.5073 | 0.3126 | 18.9885 | 28.5507 | 18.1355 | ||
注:
表 2和表 3分别给出六种Bootstrap置信区间在三个和五个总体情况下的模拟覆盖概率. 表 5和表 6分别给出六种Bootstrap置信区间在三个和五个总体情况下的模拟区间长度.就覆盖概率而言, 当偏度参数和样本量较小时,
表 5 三个总体时六种Bootstrap置信区间的模拟区间长度
| (λ1, λ2, λ3) = (3, 3, 4) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.1558 | 0.1979 | 0.1365 | 4.3721 | 6.2373 | 4.0877 | 0.1325 | 0.1794 | 0.1215 | 3.7023 | 5.2625 | 3.3734 | ||
| 0.3006 | 0.3512 | 0.2418 | 7.7139 | 11.0764 | 7.2551 | 0.2495 | 0.3182 | 0.2154 | 6.4917 | 9.3478 | 5.9910 | ||
| 0.4433 | 0.5465 | 0.3751 | 13.3325 | 17.2881 | 11.3168 | 0.4046 | 0.4949 | 0.3343 | 12.2296 | 14.5935 | 9.3507 | ||
| 1.0154 | 1.0665 | 0.7290 | 26.7962 | 33.8652 | 22.1617 | 0.7806 | 0.9649 | 0.6497 | 24.4722 | 28.5907 | 18.3170 | ||
| 1.5271 | 1.7688 | 1.2130 | 40.0428 | 56.0040 | 36.6571 | 1.3446 | 1.6015 | 1.0812 | 35.8804 | 47.2769 | 30.2912 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.1100 | 0.1527 | 0.0994 | 3.0012 | 3.9181 | 2.4516 | 0.0906 | 0.1159 | 0.0733 | 2.3937 | 3.0532 | 1.8877 | ||
| 0.2372 | 0.2708 | 0.1761 | 4.7556 | 6.9595 | 4.3525 | 0.1882 | 0.2057 | 0.1300 | 3.8212 | 5.4245 | 3.3539 | ||
| 0.3379 | 0.4209 | 0.2729 | 9.1752 | 10.8646 | 6.7914 | 0.2753 | 0.3204 | 0.2019 | 6.8204 | 8.4705 | 5.2370 | ||
| 0.5451 | 0.8201 | 0.5295 | 16.6665 | 21.2852 | 13.3020 | 0.5376 | 0.6261 | 0.3929 | 12.8209 | 16.5977 | 10.2607 | ||
| 1.2405 | 1.3619 | 0.8823 | 25.6048 | 35.1967 | 21.9996 | 0.8750 | 1.0374 | 0.6532 | 19.8941 | 27.4422 | 16.9660 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0770 | 0.0981 | 0.0608 | 1.9892 | 2.3561 | 1.4262 | 0.0687 | 0.0822 | 0.0494 | 1.8176 | 2.0390 | 1.2296 | ||
| 0.1658 | 0.1740 | 0.1077 | 2.8175 | 4.1868 | 2.5327 | 0.1298 | 0.1459 | 0.0875 | 2.7334 | 3.6225 | 2.1837 | ||
| 0.2416 | 0.2708 | 0.1668 | 5.6525 | 6.5386 | 3.9525 | 0.1859 | 0.2270 | 0.1356 | 5.1862 | 5.6567 | 3.4092 | ||
| 0.4589 | 0.5281 | 0.3235 | 10.3481 | 12.8113 | 7.7421 | 0.4102 | 0.4424 | 0.2631 | 10.0297 | 11.0841 | 6.6801 | ||
| 0.8659 | 0.8764 | 0.5392 | 13.4808 | 21.1830 | 12.8039 | 0.6102 | 0.7345 | 0.4385 | 14.6270 | 18.3261 | 11.0449 | ||
| (λ1, λ2, λ3) = (5, 5, 6) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.1407 | 0.1878 | 0.1222 | 4.0248 | 5.8983 | 3.7440 | 0.1151 | 0.1632 | 0.1041 | 3.2368 | 4.6661 | 2.9283 | ||
| 0.2739 | 0.3332 | 0.2165 | 7.0974 | 10.4754 | 6.6448 | 0.2185 | 0.2894 | 0.1845 | 5.6653 | 8.2891 | 5.2006 | ||
| 0.4017 | 0.5182 | 0.3357 | 12.3715 | 16.3519 | 10.3646 | 0.3563 | 0.4498 | 0.2864 | 10.9406 | 12.9415 | 8.1174 | ||
| 0.9341 | 1.0101 | 0.6519 | 24.9148 | 32.0333 | 20.2967 | 0.6866 | 0.8763 | 0.5565 | 21.9479 | 25.3549 | 15.9014 | ||
| 1.3924 | 1.6771 | 1.0854 | 36.9300 | 52.9723 | 33.5725 | 1.1886 | 1.4554 | 0.9262 | 31.7051 | 41.9254 | 26.2962 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0887 | 0.1279 | 0.0788 | 2.6180 | 3.3553 | 2.0751 | 0.0700 | 0.0875 | 0.0532 | 2.1090 | 2.6020 | 1.6216 | ||
| 0.1993 | 0.2269 | 0.1396 | 4.0753 | 5.9608 | 3.6841 | 0.1517 | 0.1552 | 0.0943 | 3.3151 | 4.6228 | 2.8811 | ||
| 0.2792 | 0.3524 | 0.2163 | 8.1131 | 9.3072 | 5.7488 | 0.2185 | 0.2419 | 0.1463 | 6.0298 | 7.2186 | 4.4990 | ||
| 0.4309 | 0.6860 | 0.4192 | 14.5853 | 18.2361 | 11.2604 | 0.4269 | 0.4728 | 0.2844 | 11.2715 | 14.1454 | 8.8144 | ||
| 1.0506 | 1.1400 | 0.6993 | 22.1638 | 30.1523 | 18.6226 | 0.6914 | 0.7832 | 0.4732 | 17.3326 | 23.3868 | 14.5749 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0593 | 0.0720 | 0.0437 | 1.8513 | 2.0602 | 1.2781 | 0.0558 | 0.0614 | 0.0369 | 1.7059 | 1.8071 | 1.1257 | ||
| 0.1345 | 0.1277 | 0.0774 | 2.5730 | 3.6615 | 2.2697 | 0.1069 | 0.1089 | 0.0654 | 2.5355 | 3.2111 | 1.9992 | ||
| 0.1932 | 0.1988 | 0.1197 | 5.2713 | 5.7193 | 3.5423 | 0.1503 | 0.1695 | 0.1013 | 4.8778 | 5.0149 | 3.1219 | ||
| 0.3651 | 0.3879 | 0.2319 | 9.6019 | 11.2065 | 6.9387 | 0.3410 | 0.3304 | 0.1963 | 9.4261 | 9.8271 | 6.1179 | ||
| 0.7096 | 0.6436 | 0.3869 | 12.2461 | 18.5292 | 11.4749 | 0.4951 | 0.5484 | 0.3276 | 13.6283 | 16.2471 | 10.1146 | ||
| (λ1, λ2, λ3) = (6, 8, 9) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.1374 | 0.1851 | 0.1190 | 3.8328 | 5.6934 | 3.5617 | 0.1115 | 0.1595 | 0.1006 | 3.0461 | 4.4063 | 2.7456 | ||
| 0.2679 | 0.3283 | 0.2107 | 6.7565 | 10.1120 | 6.3209 | 0.2122 | 0.2828 | 0.1783 | 5.3267 | 7.8279 | 4.8761 | ||
| 0.3922 | 0.5104 | 0.3265 | 11.8395 | 15.7855 | 9.8587 | 0.3464 | 0.4395 | 0.2767 | 10.4123 | 12.2221 | 7.6110 | ||
| 0.9154 | 0.9943 | 0.6336 | 23.8733 | 30.9242 | 19.3057 | 0.6669 | 0.8558 | 0.5375 | 20.9130 | 23.9460 | 14.9098 | ||
| 1.3617 | 1.6516 | 1.0557 | 35.2072 | 51.1376 | 31.9339 | 1.1564 | 1.4220 | 0.8948 | 29.9936 | 39.5952 | 24.6560 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0846 | 0.1226 | 0.0748 | 2.4665 | 3.1207 | 1.9302 | 0.0671 | 0.0827 | 0.0503 | 2.0203 | 2.4502 | 1.5399 | ||
| 0.1922 | 0.2175 | 0.1324 | 3.8063 | 5.5448 | 3.4270 | 0.1465 | 0.1468 | 0.0890 | 3.1575 | 4.3532 | 2.7361 | ||
| 0.2680 | 0.3377 | 0.2051 | 7.6932 | 8.6588 | 5.3476 | 0.2104 | 0.2286 | 0.1381 | 5.7836 | 6.7979 | 4.2725 | ||
| 0.4091 | 0.6571 | 0.3973 | 13.7625 | 16.9670 | 10.4745 | 0.4109 | 0.4466 | 0.2685 | 10.7888 | 13.3214 | 8.3705 | ||
| 1.0145 | 1.0923 | 0.6630 | 20.8033 | 28.0523 | 17.3230 | 0.6651 | 0.7403 | 0.4467 | 16.5347 | 22.0240 | 13.8411 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0571 | 0.0680 | 0.0415 | 1.8026 | 1.9617 | 1.2330 | 0.0543 | 0.0586 | 0.0355 | 1.6661 | 1.7271 | 1.0921 | ||
| 0.1306 | 0.1207 | 0.0734 | 2.4866 | 3.4866 | 2.1896 | 0.1043 | 0.1040 | 0.0630 | 2.4648 | 3.0692 | 1.9394 | ||
| 0.1871 | 0.1879 | 0.1136 | 5.1367 | 5.4466 | 3.4172 | 0.1462 | 0.1618 | 0.0976 | 4.7677 | 4.7936 | 3.0287 | ||
| 0.3531 | 0.3666 | 0.2198 | 9.3385 | 10.6722 | 6.6937 | 0.3329 | 0.3155 | 0.1889 | 9.2105 | 9.3939 | 5.9356 | ||
| 0.6897 | 0.6083 | 0.3669 | 11.8101 | 17.6458 | 11.0699 | 0.4818 | 0.5237 | 0.3154 | 13.2715 | 15.5304 | 9.8127 | ||
注:
表 6 五个总体时六种Bootstrap置信区间的模拟区间长度
| (λ1, λ2, λ3, λ4, λ5) = (3, 3, 4, 4, 5) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.1557 | 0.1978 | 0.1363 | 3.4939 | 4.6909 | 3.2412 | 0.1216 | 0.1617 | 0.1078 | 2.8773 | 3.4579 | 2.3837 | ||
| 0.2734 | 0.3518 | 0.2424 | 8.2839 | 11.5465 | 7.9518 | 0.2131 | 0.2876 | 0.1917 | 6.2643 | 8.7179 | 5.9407 | ||
| 0.4387 | 0.5513 | 0.3804 | 17.0336 | 22.4545 | 15.4017 | 0.3928 | 0.4504 | 0.3005 | 13.6951 | 17.0843 | 11.6810 | ||
| 1.0438 | 1.0821 | 0.7472 | 29.4770 | 38.7087 | 26.8397 | 0.7844 | 0.8838 | 0.5901 | 25.7350 | 29.3646 | 20.3567 | ||
| 1.4713 | 1.7906 | 1.2372 | 44.0148 | 60.0451 | 41.9806 | 1.2714 | 1.4625 | 0.9766 | 37.1142 | 45.4880 | 31.8257 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.1027 | 0.1398 | 0.0902 | 2.5296 | 2.8396 | 1.9479 | 0.0935 | 0.1159 | 0.0733 | 1.8318 | 2.4289 | 1.6117 | ||
| 0.2213 | 0.2485 | 0.1604 | 5.2675 | 7.0858 | 4.7783 | 0.1706 | 0.2060 | 0.1304 | 4.2271 | 5.9759 | 3.9423 | ||
| 0.3330 | 0.3895 | 0.2515 | 10.8420 | 13.8792 | 9.3431 | 0.2479 | 0.3226 | 0.2044 | 9.5049 | 11.5423 | 7.6441 | ||
| 0.5100 | 0.7648 | 0.4939 | 21.4102 | 24.0453 | 16.3943 | 0.5928 | 0.6331 | 0.4013 | 17.7956 | 20.1387 | 13.4950 | ||
| 0.9985 | 1.2659 | 0.8175 | 26.7238 | 37.3193 | 25.6653 | 0.8089 | 1.0476 | 0.6642 | 22.7187 | 31.3854 | 21.2205 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0822 | 0.1093 | 0.0687 | 1.7325 | 2.0830 | 1.3409 | 0.0628 | 0.0822 | 0.0494 | 1.6502 | 1.6998 | 1.0693 | ||
| 0.1728 | 0.1943 | 0.1221 | 3.6881 | 5.0325 | 3.3183 | 0.1143 | 0.1462 | 0.0879 | 3.3868 | 4.1695 | 2.6306 | ||
| 0.2729 | 0.3044 | 0.1915 | 8.6829 | 9.8244 | 6.4719 | 0.1815 | 0.2290 | 0.1378 | 8.1659 | 8.2079 | 5.2124 | ||
| 0.5130 | 0.5974 | 0.3761 | 16.8130 | 17.2494 | 11.4077 | 0.4510 | 0.4493 | 0.2705 | 14.5028 | 14.2889 | 9.0520 | ||
| 0.7733 | 0.9888 | 0.6224 | 24.5885 | 26.9702 | 17.9168 | 0.5895 | 0.7434 | 0.4476 | 16.8295 | 22.2257 | 14.1171 | ||
| (λ1, λ2, λ3, λ4, λ5) = (4, 4, 5, 5, 6) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.1462 | 0.1915 | 0.1272 | 3.2911 | 4.4496 | 3.0456 | 0.1088 | 0.1479 | 0.0948 | 2.7034 | 3.2557 | 2.2115 | ||
| 0.2565 | 0.3406 | 0.2263 | 7.8440 | 11.0346 | 7.5213 | 0.1904 | 0.2630 | 0.1686 | 5.8552 | 8.2163 | 5.5371 | ||
| 0.4124 | 0.5337 | 0.3552 | 16.2008 | 21.4728 | 14.5817 | 0.3571 | 0.4118 | 0.2644 | 12.8877 | 16.0774 | 10.8849 | ||
| 0.9921 | 1.0475 | 0.6977 | 27.9733 | 36.9794 | 25.3735 | 0.7145 | 0.8081 | 0.5192 | 24.2983 | 27.6426 | 18.9434 | ||
| 1.3857 | 1.7332 | 1.1552 | 41.6062 | 57.3327 | 39.6393 | 1.1556 | 1.3371 | 0.8594 | 34.8158 | 42.8044 | 29.5654 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0880 | 0.1214 | 0.0758 | 2.3754 | 2.6513 | 1.7957 | 0.0791 | 0.0964 | 0.0591 | 1.7105 | 2.2721 | 1.4887 | ||
| 0.1951 | 0.2159 | 0.1348 | 4.9387 | 6.6647 | 4.4483 | 0.1449 | 0.1714 | 0.1051 | 3.9676 | 5.6446 | 3.6908 | ||
| 0.2919 | 0.3383 | 0.2114 | 10.1844 | 13.0444 | 8.6890 | 0.2077 | 0.2684 | 0.1648 | 8.9952 | 10.9070 | 7.1541 | ||
| 0.4294 | 0.6643 | 0.4151 | 20.2033 | 22.5874 | 15.1945 | 0.5139 | 0.5266 | 0.3234 | 16.8518 | 19.0010 | 12.5837 | ||
| 0.8652 | 1.0995 | 0.6871 | 24.7762 | 35.0130 | 23.7310 | 0.6784 | 0.8714 | 0.5352 | 21.1760 | 29.5517 | 19.7318 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0696 | 0.0912 | 0.0561 | 1.6539 | 1.9649 | 1.2599 | 0.0532 | 0.0672 | 0.0400 | 1.6002 | 1.6103 | 1.0197 | ||
| 0.1504 | 0.1622 | 0.0998 | 3.5044 | 4.7685 | 3.1352 | 0.0973 | 0.1195 | 0.0712 | 3.2736 | 3.9771 | 2.5161 | ||
| 0.2378 | 0.2540 | 0.1565 | 8.3027 | 9.2860 | 6.0901 | 0.1548 | 0.1872 | 0.1116 | 7.9416 | 7.8271 | 4.9874 | ||
| 0.4440 | 0.4984 | 0.3073 | 16.1106 | 16.2937 | 10.7029 | 0.3986 | 0.3673 | 0.2191 | 14.0896 | 13.6050 | 8.6378 | ||
| 0.6591 | 0.8249 | 0.5084 | 23.4391 | 25.4566 | 16.7651 | 0.5028 | 0.6077 | 0.3626 | 16.1526 | 21.1227 | 13.4314 | ||
| (λ1, λ2, λ3, λ4, λ5) = (7, 7, 8, 8, 9) | |||||||||||||
| N1 | N2 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.1355 | 0.1836 | 0.1170 | 3.0581 | 4.1632 | 2.8178 | 0.0949 | 0.1315 | 0.0811 | 2.5129 | 3.0279 | 2.0208 | ||
| 0.2374 | 0.3266 | 0.2081 | 7.3303 | 10.4187 | 7.0135 | 0.1657 | 0.2338 | 0.1442 | 5.4125 | 7.6619 | 5.1002 | ||
| 0.3824 | 0.5116 | 0.3267 | 15.2237 | 20.2877 | 13.6218 | 0.3185 | 0.3661 | 0.2264 | 11.9978 | 14.9555 | 10.0096 | ||
| 0.9334 | 1.0040 | 0.6417 | 26.2275 | 34.9196 | 23.6569 | 0.6387 | 0.7184 | 0.4446 | 22.7218 | 25.7450 | 17.3886 | ||
| 1.2886 | 1.6610 | 1.0626 | 38.8013 | 54.0965 | 36.9026 | 1.0302 | 1.1885 | 0.7359 | 32.3204 | 39.8907 | 27.1060 | ||
| N3 | N4 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0747 | 0.1028 | 0.0627 | 2.2214 | 2.4616 | 1.6481 | 0.0685 | 0.0801 | 0.0486 | 1.5998 | 2.1215 | 1.3816 | ||
| 0.1715 | 0.1827 | 0.1114 | 4.6076 | 6.2369 | 4.1287 | 0.1260 | 0.1424 | 0.0865 | 3.7212 | 5.3159 | 3.4558 | ||
| 0.2548 | 0.2864 | 0.1748 | 9.5321 | 12.1893 | 8.0624 | 0.1780 | 0.2230 | 0.1356 | 8.5029 | 10.2646 | 6.6820 | ||
| 0.3566 | 0.5624 | 0.3432 | 18.9937 | 21.1033 | 14.0387 | 0.4556 | 0.4376 | 0.2662 | 15.9378 | 17.8566 | 11.7123 | ||
| 0.7446 | 0.9308 | 0.5684 | 22.8372 | 32.6800 | 21.8718 | 0.5819 | 0.7240 | 0.4405 | 19.6857 | 27.7385 | 18.3212 | ||
| N5 | N6 | ||||||||||||
| Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | Zmple | Zmle | Zmm | Tmple | Tmle | Tmm | ||
| 0.0593 | 0.0757 | 0.0464 | 1.5813 | 1.8492 | 1.1884 | 0.0476 | 0.0571 | 0.0347 | 1.5523 | 1.5169 | 0.9747 | ||
| 0.1321 | 0.1346 | 0.0825 | 3.3250 | 4.5016 | 2.9623 | 0.0873 | 0.1015 | 0.0617 | 3.1667 | 3.7736 | 2.4147 | ||
| 0.2092 | 0.2109 | 0.1294 | 7.9352 | 8.7334 | 5.7341 | 0.1391 | 0.1589 | 0.0967 | 7.7241 | 7.4248 | 4.7839 | ||
| 0.3879 | 0.4137 | 0.2540 | 15.4452 | 15.3345 | 10.0587 | 0.3678 | 0.3118 | 0.1899 | 13.7053 | 12.8871 | 8.2708 | ||
| 0.5663 | 0.6848 | 0.4202 | 22.3662 | 23.9540 | 15.7304 | 0.4518 | 0.5158 | 0.3143 | 15.5373 | 19.9767 | 12.8403 | ||
注:
5 案例分析
为了验证本文所给方法的合理性和有效性, 本小节将其应用于地区GDP和生物利用度数据的案例分析.
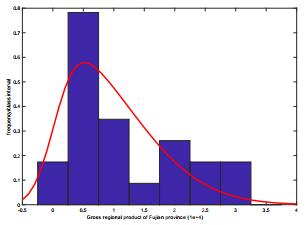
案例1 我们将上述方法应用于1995-2017年福建省和湖北省GDP数据.由图 1和图 2可见, 福建省和湖北省GDP数据均不服从正态分布且明显呈现出非对称、右偏的分布特征.为检验该结论的正确性, 对数据进行Shapiro-Wilk、Anderson-Darling和Kolmogorov-Smirnov正态性检验.结果表明:福建省GDP数据的
图 1
图 2
进一步, 我们考虑假设检验问题
在原假设
类似于
基于
可得基于
案例2 现对生物利用度进行研究, 将20名试验人员随机分成两个平行组进行实验, 以比较新的测试制剂(x)和具有长半衰期的药物产品的参考制剂(y).在统计分析中, 构造两种试剂的峰浓度(Cmax)位置参数置信区间对于确定是否具有不同的生物利用度非常重要. Wu等[28]分析了两组Cmax数据的特征, 认为这些数据的分布是高度正偏斜的.进一步, 对该数据进行偏正态分布检验, 即检验原假设
我们考虑假设检验问题
计算出Bootstrap检验统计量的
得出基于
6 结论
本文针对多个具有共同位置参数的偏正态总体, 当尺度参数和偏度参数未知时, 基于Bootstrap方法研究位置参数的区间估计和假设检验问题.首先, 分别给出未知参数的矩估计和极大似然估计.其次, 将徐礼文[1]对多个正态总体共同均值的探讨推广到多个偏正态总体, 进而构造共同位置参数的Bootstrap置信区间和Bootstrap检验统计量.再次, Monte Carlo模拟结果表明, 无论是两个总体、三个总体还是五个总体, 基于矩估计和惩罚极大似然估计的Bootstrap置信区间在覆盖概率意义下优于其他四种Bootstrap置信区间.最后, 将上述方法应用于地区生产总值和生物利用度数据的案例分析, 以验证本文所给方法的合理性和有效性.综上所述, 针对多个偏正态总体共同位置参数的统计推断问题, 本文建议优先应用基于矩估计和惩罚极大似然估计的Boostrap方法.
参考文献
A class of distributions which includes the normal ones
Further results on a class of distributions which includes the normal ones
Characterizations of the skew-normal and generalized chi distributions
Characteristic functions of scale mixtures of multivariate skew-normal distributions
DOI:10.1016/j.jmva.2011.03.004 [本文引用: 1]
Distribution of matrix quadratic forms under skew-normal settings
DOI:10.1016/j.jmva.2014.07.001 [本文引用: 1]
Multivariate measures of skewness for the skew-normal distribution
DOI:10.1016/j.jmva.2011.06.017 [本文引用: 1]
Asymptotic expansions for moments of skew-normal extremes
DOI:10.1016/j.spl.2013.02.010 [本文引用: 1]
The exact density of the sum of independent skew normal random variables
Estimation of location parameter in the skew normal setting with known coefficient of variation and skewness
Statistical inference for the location and scale parameters of the skew normal distribution
DOI:10.1007/s13226-018-0291-6 [本文引用: 1]
The Inference on the Location Parameters under Multivariate Skew Normal Settings//Kreinovich V, Thach N, Trung N, Thanh D
Testing hypotheses about the common mean of normal distributions
DOI:10.1016/0378-3758(84)90022-3 [本文引用: 1]
Combining independent tests in multivariate linear models
Confidence regions for the common mean vector of several multi-variate normal populations
DOI:10.2307/3315368
Exact confidence intervals for the common mean of several normal populations
DOI:10.2307/2533146
Inferences on the common mean of several normal populations based on the generalized variable method
Generalized inferences on the common mean of several normal populations
DOI:10.1016/j.jspi.2004.02.018
Generalized inferences on the common mean vector of several multivariate normal populations
DOI:10.1016/j.jspi.2006.07.005
An identity for exponential distributions with the common location parameter and its applications
Generalized inferences on the common mean in MANOVA models
Inferences on the common mean of several inverse Gaussian populations
DOI:10.1016/j.csda.2009.09.039 [本文引用: 1]
Modelling asymmetrically distributed circular data using the wrapped skew-normal distribution
The centred parametrization for the multivariate skew-normal distribution
DOI:10.1016/j.jmva.2008.01.020
Problems of inference for Azzalini's skewnormal distribution
DOI:10.1080/02664760050120542 [本文引用: 2]
Combining unbiased estimators
Maximum penalized likelihood estimation for skew-normal and skew-t distributions
DOI:10.1016/j.jspi.2012.06.022 [本文引用: 1]
Likelihood analysis for the ratio of means of two independent log-normal distributions
DOI:10.1111/j.0006-341X.2002.00463.x [本文引用: 1]