1 引言
设
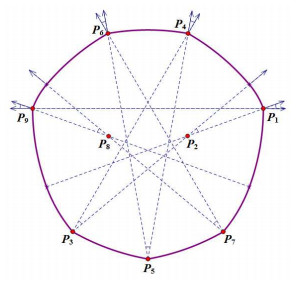
常宽凸集的概念由欧拉首次提出. 1876年, Reuleaux构造了以正三角形三个顶点为圆心, 边长为半径的外接圆弧组成的非圆的常宽曲线, 人们称之为Reuleaux三角形.该方法被推广在奇数边正多边形上得到Reuleaux正多边形.之后, Meissner将Reuleaux三角形推广至三维空间, 构造出两种不同的三维常宽凸集[1-2]. 1915年, Blaschke与Lebesgue分别证明了平面上等宽度的常宽凸体中Reuleaux三角形面积最小, 这个定理就是著名的Blaschke-Lebesgue定理.对于这个命题, 国内外的数学家们又先后给出了其它巧妙的证明[1,3-5].数学家十分关注Blaschke-Lebesgue定理的高维情形, 并提出了Blaschke-Lebesgue问题, 即高维等宽度的常宽凸体中谁的体积最小.长久以来, 人们猜测Meissner体是三维Blaschke-Lebesgue问题的解, 但至今未被证明.为此, 数学家不断尝试构造新的常宽凸集并研究其几何性质. 2003年, 潘生亮教授在文献[6]中利用Minkowski支撑函数得到了一类新的光滑的常宽凸集. 2007年, Lachand-Robert与Qudet用数学归纳法给出了一种
本文将讨论如何构造平面常宽曲线.为此, 我们首先定义了一类平面曲线, 称为杠杆轮(见正文中定义3.1), 并利用臂函数(见正文中第3节)给出杠杆轮的参数表示.其次, 我们证明了杠杆轮是平面常宽曲线的一种等价刻画.最后, 我们构造了一类臂函数为三角函数形式的常宽曲线, 并表明广义Reuleaux多边形(即由若干段圆弧围成的平面常宽凸体)是臂函数为分段常函数的一类杠杆轮.在此基础上, 构造了具体的广义Reuleaux多边形, 特别是偶数边的广义Reuleaux多边形.
2 基本概念
记
定义2.1 设
为
当
定义2.2 设
一般地, 称
设
3 杠杆轮的定义及参数方程
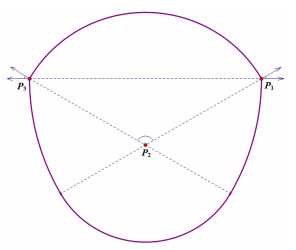
一般地, 常宽曲线由极值点构成, 即一个常宽曲线与其在任意方向上支撑线的交都为单点集(极值点定义参见文献[9]).因此, 设
(ⅰ)
特别地, 当
(ⅱ)
下面我们将对局部具有性质(ⅰ)和(ⅱ)的曲线进行研究.
定义3.1 设
其中
注3.1 杠杆轮
设
结合定义3.1中的条件(ⅱ), 可得
由(3.2)式, 可得
由
因此,
由
为杠杆轮
引理3.1 对任意的
证 由定义3.1中的条件(ⅰ)与(3.3)式, 可得
由定义3.1中条件(ⅱ)与(3.4)式, 可得
即
因为
记
注3.2 可以看出, 杠杆轮
且由引理3.1中的条件(ⅰ)可得
注3.3 对任意
注3.4 设杠杆轮
定理3.1(杠杆轮的参数方程) 若
且
其中
反过来, 若
为杠杆轮.
证 (1)
结合(3.4)式可得
令
当
结合定义3.1中的条件(ⅱ), 则有
结合引理3.1可知臂函数
(2) 设函数
首先, 证明曲线
即
结合性质(ⅱ)可得
其次, 由步骤(1)的证明过程可以看出(3.6)式成立, 进而(3.5)式也成立, 故定义3.1中的条件(ⅰ)成立.下面证明定义3.1中的条件(ⅱ)也是成立的.
任意取定
当
令
4 杠杆轮是常宽曲线的等价刻画
上一节通过观察Reuleaux多边形的特征定义了一类平面曲线:杠杆轮.本节将证明杠杆轮是常宽曲线的一种等价刻画.
引理4.1 下列各条款等价
证 (ⅰ)
(ⅱ)
令
由
令
这与定义2.2矛盾, 故(ⅱ)
(ⅲ)
看出,
同理
因此
同理,
若将
因为
故
(ⅱ)
对
进而
事实上, 若
因此
引理4.2 设曲线
证 设
其中
当
当
当
故
下面证明
令
进而,
定理4.1(常宽曲线的等价刻画)
证 充分性.设
由定义3.1中的条件(ⅱ)可得
故杠杆轮为广义常宽集.进一步, 结合已知条件
必要性.设
由引理4.1中步骤(ⅲ)
即
显然,
同理,
设
解得
若任意给定
又
5 平面常宽凸体的构造
下面我们利用定理3.1和定理4.1构造一类平面常宽曲线.设
其中
结合定理3.1和定理4.1可以证明, 函数
是杠杆轮(或常宽曲线)的臂函数当且仅当齐次线性方程组
成立且非零常数
记
利用(5.1), (5.2)和(5.5)式可以得到
其中
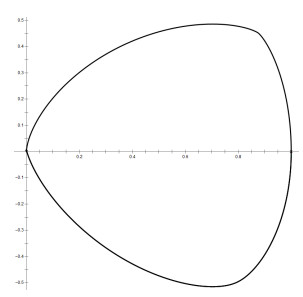
例5.1 当
其中
图 1
例5.2 当
其中
图 2
我们把包含圆与Reuleaux多边形在内的所有可以分割为若干段圆弧的常宽曲线统称为广义Reuleaux多边形.下面我们讨论广义Reuleaux多边形的构造.由定理3.1和定理4.1可知, 对任意宽度为
定理5.1 任意广义
证 首先, 设
设
且对任意
即在
其次, 设
其中右开区间
是半径为
事实上, 构造广义Reuleaux多边形就是构造臂函数为分段常函数的杠杆轮.为此, 我们设
其中右开区间
结合定理3.1和定理5.1可以证明, 若
成立且非零常数
则分段常函数
是广义Reuleaux多边形的臂函数.反之, 若任意广义Reuleaux多边形的臂函数
设分段常函数
是广义Reuleaux多边形
易看出, 当常数
其中非负整数
综上所述, 将区间
例5.3 将区间
设直径长度
图 3
例5.4 将区间
设直径长度
图 4
6 小结
为了构造平面常宽凸体, 我们基于Reuleaux多边形的性质定义了一类平面曲线, 称为杠杆轮, 它是平面常宽曲线的一种等价刻画.我们引入了杠杆轮的臂函数, 用臂函数给出了杠杆轮的参数表示, 从而给出了常宽曲线的一种不同于支撑函数表示的参数方程.特别地, 本文定义的臂函数区别于支撑函数.首先, 臂函数不依赖于原点位置.其次, 可以用臂函数的积分表示曲线参数方程, 不要求臂函数的连续性, 并且比支撑函数更便于构造Reuleaux多边形.
另外, 本文构造了一类臂函数为三角函数形式的常宽曲线, 并且推广了经典的Reuleaux多边形, 得到了广义Reuleaux多边形.
参考文献
Über Punktmengen konstanter Breite
Analytic proof of Blaschke's theorem on the curve of constant breadth with minimum area
A direct proof of a theorem of Blaschke and Lebesgue
DOI:10.1007/BF02930861 [本文引用: 1]
切线极坐标的一个应用
An application of the polar tangential coordinate
Bodies of constant width in arbitrary dimension
DOI:10.1002/mana.200510512 [本文引用: 1]
一类常宽"等腰梯形"
DOI:10.3969/j.issn.0253-2778.2011.10.002 [本文引用: 1]
On the isosceles trapezoids of constant width
DOI:10.3969/j.issn.0253-2778.2011.10.002 [本文引用: 1]