1 引言
设
显然, 张量的爱因斯坦积满足结合律.本文记
其中
进一步, 记对角张量为
其中
记
在文献[6]中, Ji和Wei提出偶数阶张量的加权Moore-Penrose逆.
设
记
如果方阵
2 预备知识
定义2.1[17] 设
记
引理2.1[17] 设
(1)
(2)
引理2.2[17] 设
且
定义2.2[17] 设
(ⅰ)
(ⅱ)
(ⅲ)
(ⅳ)
(ⅴ)
其中
注2.1 由文献[15, 引理3.2]有
引理2.4[19] 设
其中
进一步得
注2.2 设
应用
注2.3 如果
引理2.5 设
(ⅰ)
(ⅱ)
(ⅲ)
(ⅳ)
证 应用(2.1)式和
应用
应用(2.1)式和
以及
应用(2.1)式和
应用
应用(2.1)式和
以及
3 张量core逆的性质
定理3.1 设
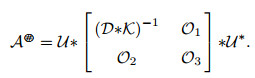
证 设
设
其中
定理3.2 设
(ⅰ)
(ⅱ)
证 由于
得到
由于
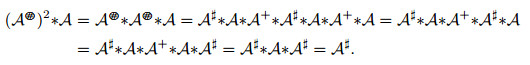
定理3.2得证.
定理3.3 设
则
证 由定理3.1, 有
和
由于
以及
引理3.1 设
则
证 由于
定理3.4 设
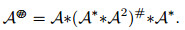
证 设
应用引理3.1, 我们知道
是可逆的.因此得到
应用(2.1)式和
即
4 张量偏序
矩阵偏序是满足自反性、传递性和反对称性的二元关系.以下是三种重要的矩阵偏序.
第一种偏序是由Hartwing在文献[5]提出的减序
第二种偏序是由Mitra在文献[14]中提出的sharp序
第三种偏序是由Baksalary和Trenkler在文献[1]提出的core序
类似于矩阵偏序, 我们称在张量上满足下述三个条件的二元关系
(1) 自反性,
(2) 对称性, 若
(3) 传递性, 若
在本节, 我们考虑张量的偏序并研究张量偏序的性质和刻画等.
定义4.1 设
的二元关系
以下定理证明
定理4.1
证 自反性显然成立.
设
设
即
定义4.2 设
的二元关系为
为了证明
引理4.1 设
其中
证 设
因此,
知道,
引理4.2 设
其中
证 假设
由
即
由
由
即
由
即
由
由(4.27), (4.29)和(4.31)式, 得到
由(4.30)式,
进而由(4.26)式, 得到
证毕.
定理4.2 T-core序是一个张量偏序.
证 为了证明
由张量core满足{2}逆和(4.32)式第二个等式的右边, 得到
通过比较(4.6)和(4.33)式, 得到了
(ⅲ), 设
通过应用(4.34)和(4.35)式的第二个等式和引理2.1, 有
由(3.1)式, 得到了
类似地, 应用(4.34)和(4.35)式的第一个等式和引理2.1, 得到
此外, 引理2.1和引理2.2, 得到
由(3.1), (4.6)和(4.37)式, 得到
即
定理4.3 若
证 由引理2.1, (4.5)式的第一个条件可写为
5 张量方程
设
有解, 则通解为
其中
定理5.1 设
证 由于

则
其中
因而
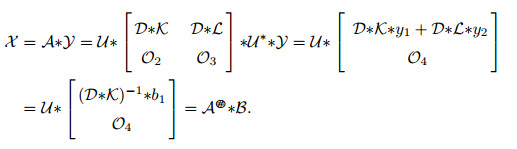
定理5.1证毕.
参考文献
Core inverse of matrices
DOI:10.1080/03081080902778222 [本文引用: 3]
Solving multilinear systems via tensor inversion
DOI:10.1137/100804577 [本文引用: 1]
Characterizations and representations of core and dual core inverses
DOI:10.4153/CMB-2016-045-7 [本文引用: 1]
Weighted Moore-Penrose inverses and the fundamental theorem of even-order tensors with Einstein product
The Drazin inverse of an even-order tensor and its application to singular tensor equations
DOI:10.1016/j.camwa.2018.02.006 [本文引用: 1]
The generalized inverses of tensors and an application to linear models
DOI:10.1016/j.camwa.2017.04.017
爱因斯坦积下张量的加权Moore-Penrose逆的扰动理论
Perturbation theory for weighted Moore-Penrose inverse of tensors via Einstein product
Revisitation of the core inverse
DOI:10.1007/s11859-015-1109-6 [本文引用: 1]
Some more properties of core partial order
An order-p tensor factorization with applications in imaging
Generalized tensor function via the tensor singular value decomposition based on the T-product
DOI:10.1016/j.laa.2019.12.035 [本文引用: 1]
On group inverses and the sharp order
DOI:10.1016/0024-3795(87)90248-5 [本文引用: 1]
Outer and
DOI:10.1080/03081087.2018.1521783 [本文引用: 2]
Group, Moore-Penrose, core and dual core inverse in rings with involution
Core and core-EP inverses of tensors
DOI:10.1007/s40314-019-0983-5 [本文引用: 6]
Moore-Penrose inverse of tensors via Einstein product
DOI:10.1080/03081087.2015.1083933 [本文引用: 3]
Perturbation bounds for DMP and CMP inverses of tensors via Einstein product
DOI:10.1007/s40314-019-0964-8 [本文引用: 1]
Characterizations of the core inverse and the core partial ordering
DOI:10.1080/03081087.2014.975702 [本文引用: 2]
The accelerated overrelaxation splitting method for solving symmetric tensor equations
DOI:10.1007/s40314-019-0964-8 [本文引用: 1]


