1 引言
种群动力学模型是对生物种群演化过程的近似模拟(精确模拟几乎是不可能的).因此, 模型的平衡态及其稳定性就相应地表征了种群的生态平衡及其稳定性.演化过程的复杂性决定了模型的非线性特点.众所周知:非线性系统的稳定性分析绝非易事.就具有个体特征结构差异的连续种群模型而言, 挑战性就更强, 因为模型通常形为非线性偏微分-积分方程或方程组, 并附有全局反馈的边界条件.目前, 国内外学者对这类模型进行了较为深入的研究, 获得了许多深刻结果, 它们对预测种群演化趋势、生物多样性保护、抑制生物入侵、科学开发生物资源等方面都具有良好的指导意义.对年龄结构模型可参见文献[1-7]及其所引文献, 尺度结构模型参见文献[8-11]及其所引文献.从数学观点看, 尺度(长度、表面积、体积、重量等)结构模型是年龄结构模型的拓展, 二者都是有趣又困难的研究对象.
作为种群中个体社会地位的模拟, 等级结构模型在近二十年受到了较多关注.尽管取得了一些成果, 但与年龄结构、尺度结构模型的相应成果比较, 对等级结构模型的研究还远不完善.值得强调的是:由于年龄和尺度是影响个体等级的两种主要因素, 等级结构模型也是年龄结构模型与尺度结构模型的进一步拓展, 理论分析难度更大一些.有关等级结构模型的平衡态及其稳定性成果较为少见.文献[12]分析一类尺度等级结构模型的稳定性, 具有零边界条件:文献[13]针对一类离散等级结构模型给出了稳定性判据.本文力图研究一类非线性等级结构模型的平衡态与稳定性, 等级由年龄确定, 具有非零的全局反馈边界条件.主要关注正平衡态的存在性, 以往用于确立年龄结构、尺度结构模型正平衡态的方法已不再适用.本文运用文献[2]中的非零元不动点定理证明系统存在正平衡态, 并对零解的稳定性作细致分析.
2 正平衡态的存在性
本文旨在探索下列非线性等级结构种群模型平衡态的存在性与稳定性
其中
本文的分析过程需要下列条件
(H1) 对任意
(H2) 对任意
(H3) 函数
非负函数
由系统
由此易知:
当
通常被称作该种群相应于
为了证明系统
引理2.1 令
(1) 对任意满足
(2) 存在
那么映射
定理2.1 当
取Banach空间
定义映射
第一步:证明下列结果.
引理2.2 映射F是连续的.
证 设
由系统
即
另一方面, 有
其中
第二步:证明
引理2.3(Fréchet-Kolmogorov) 假设
证 为了应用引理2.3, 将
从而
同理, 由
再证
其中
当
由此即得
最后证明
利用
对
第三步:证明当
证 若
由
下面只考虑
(1)
从而
(2)
再由
利用
第四步:证明
证 用反证法, 分四种情形处理.
(1)
由映射
当
(2)
令
(3)
令
(4)
当
综合以上分析知:引理2.1中的所有条件都满足.因此, 映射
3 零平衡态的稳定性
系统(2.1)在零平衡态处的线性化结果如下
下面推导零平衡态的特征方程.考虑系统
解得
由此利用系统
易知
另一方面, 当
推出矛盾.因此当
再假设
其中应用了
注意到
定理3.1 (1)当
(2) 当
4 数值模拟
例1(零平衡态渐近稳定) 选定参数如下:
个体繁殖率
若种群初始分布为
计算可得
若其它参数相同, 则相应于初始分布
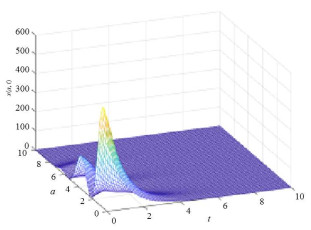
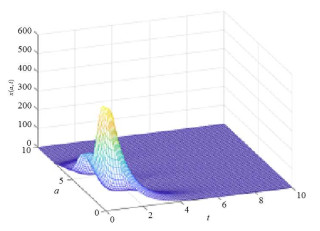
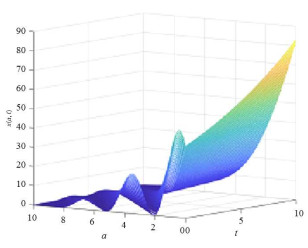
通过计算绘制下列图形, 显示零平衡态的稳定性, 与定理3.1中的结论(2)一致.
图 1
图 2
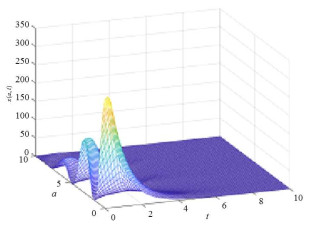
例2(零平衡态不稳定) 选定参数如下:
个体死亡率
个体繁殖率
图 3
图 4
图 5
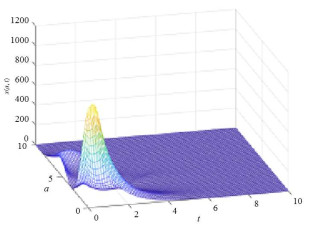
相应于参数组:
个体繁殖率
可得
图 6
5 讨论
定理2.1为正平衡态的存在性建立了判别方法, 其中主要条件是
参考文献
Non-linear age-dependent population dynamics
DOI:10.1007/BF00250793 [本文引用: 1]
On the qualitative behaviour of populations with age-specific interactions
DOI:10.1016/0898-1221(83)90020-2 [本文引用: 1]
Stability of nonlinear age-dependent population model containing a control variable
Dynamics of age-structured predator-prey population models
The stability of nonlinear age-dependent population equation
On the stability of the cell size distribution
DOI:10.1007/BF00277748 [本文引用: 1]
Stability conditions for a non-linear size-structured model
DOI:10.1016/j.nonrwa.2004.06.003
Stability results for a size-structured population model with resources-dependence and inflow
DOI:10.1016/j.jmaa.2009.07.005
具有尺度结构和双加权的种群模型:稳定性与最优收获
A weighted population model with size-structure:Stability and optimal harvesting
Steady states in hierarchical structured populations with distributed states at burth
DOI:10.3934/dcdsb.2012.17.2671 [本文引用: 1]
The global dynamics of a discrete nonlinear hierarchical population system
DOI:10.1142/S1793524519500220 [本文引用: 1]
一类非线性等级结构种群控制模型解的适定性
The well-posedness of a nonlinear age-structured population control model
一类非线性等级结构种群模型的数值解法
Numerical method od a nonlinear hierarchical age-structured population model