1 引言
在Bardeen-Cooper-Schrieffer(BCS)量子超导理论中超导状态被一个正的能隙函数所刻画, 记为
为了叙述的方便, 通常考虑BCS模型的一维情形:
其中
当核函数
文献[2]中给出了一些数值结果: BCS方程(1.1)有一个正解
然而, 条件(1.3)是一种简单的假设, 为了使模型更接近实际, Bogoliubov, Tolmachev和Shirkov在文献[1]中提出了如下模型:
其中, 区间变为
注1.1 问题(1.4)–(1.5)通常被称为Bogoliubov-Tolmachev-Shirkov (BTS)模型, 它是BCS模型的一个自然延伸.
文献[2]基于核函数恒正的数值方法对于核函数变号的情况不能使用, 为此, 我们提出一种新的数值方法求解具有变号核函数问题(1.4)的临界温度和能隙解.我们设计了最小-混合格式和最大-混合格式, 同时证明了存在两个相应的数值临界温度
2 BTS模型的数值方法
记
引入变量
注2.1 由文献[11]可知存在一个唯一的正的转变温度,
下面, 我们给出确定临界温度的数值方法.首先, 对区间
然后, 我们分两种情况来处理问题:
情况Ⅰ
问题(1.4)的下方逼近离散格式是
其中
格式(2.3)的解被记为:
问题(1.4)的上方逼近离散格式为
其中
格式(2.6)的解记为:
注2.2 格式(2.3)的最小-混合离散格式和格式(2.6)最大-混合离散格式是新的, 对文献[2]中的格式有本质的改进.
为了说明数值解的收敛性, 需要给出以下引理.为了方便, 记
引理2.1 令
对于每一个固定的
证 证明类似于[11]中的情形, 此处略去.
记
则易证下面的引理成立.
引理2.2
引理2.3 如果
证 因为函数
由(2.10)式, 可得存在一个常数
由(2.11)式和引理2.1可知, 如果
引理2.4 如果
证 从(2.7)式, 容易验证
由(2.12)和(2.3)式, 易知当
在格式(2.3)中令
在
引理2.5 如果
证 由引理2.3可知, 存在一个绝对常数
令
不妨假设存在某个正数
由(2.17)式可知
由(2.3)式, (2.18)式和引理2.1, 可得
由(2.19)式, 可得
由(2.3)式, (2.20)式和引理2.2, 可得
由(2.14)式, 若
由数学归纳法原理, (2.16)和(2.17)式普遍成立.
由格式(2.3)的第二个方程可知, 数列
令
引理2.6
证 为了证明结论成立, 只需要说明:如果
由格式(2.3), 可知
结合(2.23)和(2.24)式, 可得
在(2.4)式中, 令
综合利用引理2.4, 引理2.5和引理2.6, 可得到如下结果:
定理2.1 在
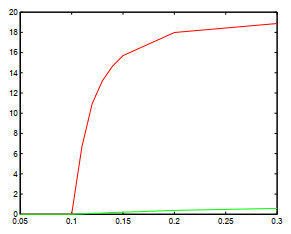
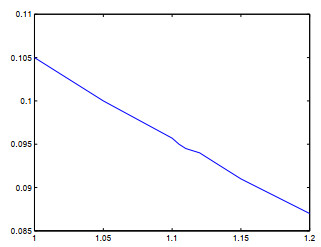
图 1
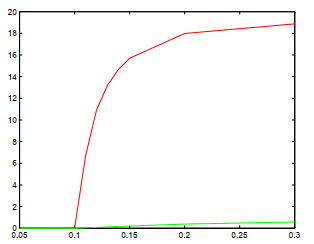
图 4
图 4
最小-混合格式(
对于格式(2.6), 采用与定理2.1类似的证明, 可以得到以下结果:
定理2.2 在
此外, 我们有以下重要的比较定理:
定理2.3 若
而且, 令
证 由(2.2), (2.3)和(2.6)式, 容易验证(2.26)式成立.
下面, 我们验证(2.27)式成立.由定理2.1, 对任意给出的
由(2.26)式, 可知
同理, 可得
由(2.28)和(2.29)式, 可得(2.27)式成立.证毕.
情况Ⅱ
对于这种情况, 我们需要将格式(2.2)重写为以下形式:
对于(2.30)式, 其最小-混合格式为
其中
其最大-混合格式为
类似于情况Ⅰ, 可以定义如下符号:
按照格式(2.3)的方法, 可以得到与定理2.1, 定理2.2和定理2.3相似的结果, 具体细节略去.
综上, 可以得出结论:最小-混合格式从下方逼近了系统(2.2)的临界温度和能隙解的近似解, 而最大-混合格式则从上方逼近了系统(2.2)的临界温度和能隙解的近似解.
3 数值算例
在这一节中, 我们给出了一些算例来验证本文所设计的数值方法的有效性.
算例1 首先选取参数
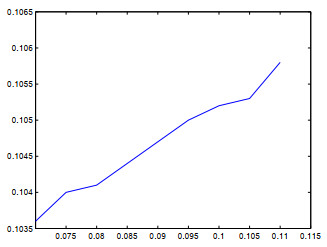
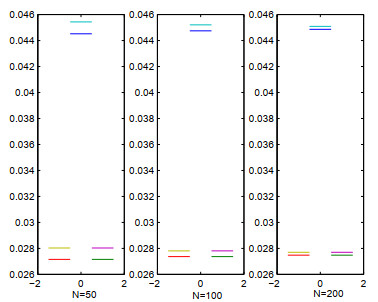
图 2
图 2
最大-混合格式(从上到下), 最小-混合格式(从下到上), u (left), v (right), \beta = 6, N = 50, 100, 200
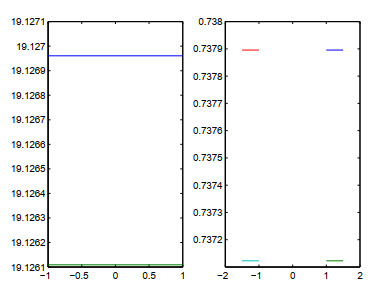
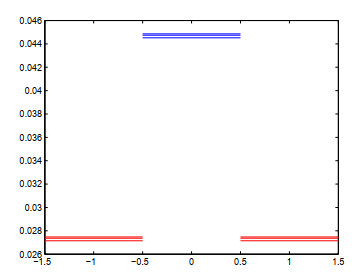
图 3
下面, 我们只改变
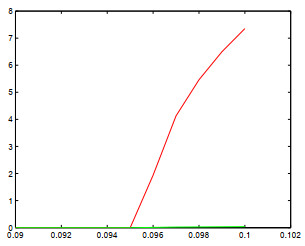
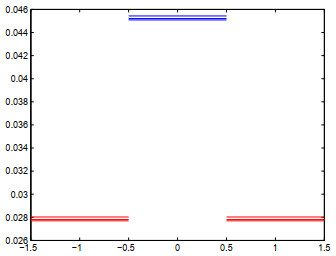
图 5
图 5
最小-混合格式(
图 6
现在, 我们只改变
通过图 7, 我们看到
图 7
算例2 令
图 8
图 9
图 10
图 11
下面, 我们只增加
图 12表明:当
图 12
现在, 我们只改变
图 13表明:
图 13
从图中可以看出, 数值算例验证了本文的理论结果, 也与相应的物理现象吻合得很好.
参考文献
A new method in the theory of superconductivity
The critical temperature and gap solution in the Bardeen-Cooper-Schrieffer theory of superconductivity
The BCS gap equation for spin-polarized Fermions
Critical temperature and energy gap for the BCS equation
Linear fermion systems, molecular field models, and the KMS condition
The modern theory of superconductivity
The solution to the BCS gap equation for superconductivity and its temperature dependence
On the Bardeen-Cooper-Schrieffer integral equation in the theory of superconductivity
Rigorous proof of isotope effect by Bardeen-Cooper-Schrieffer theory