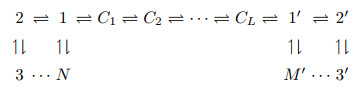连续时间齐次马尔可夫链在我国得到了系统深入的研究, 参见文献[4, 15, 22, 26, 33], 并且已经广泛应用于各个领域, 包括生物、工程、经济管理、社会管理等, 例如, 离子通道的马尔可夫链模型、商品折旧率的马尔可夫链模型、受马尔可夫链调控的风险模型^[1]等.现实系统中, 潜在的马尔可夫链（例如调控风险模型的潜在马尔可夫链)的转移速率(或概率)是怎样的?可能恰恰就是首先要通过少数状态观测的数据来确认的, 例如, 确定由连续时间马尔可夫链建模的离子通道的门控动力学就是这种实际应用于生物物理学的典型例子, 参见文献[5]及进一步的文献.因此, 如何利用部分可观测数据确认潜在的马尔可夫链的转移速率矩阵在实际应用中起着非常重要的作用, 称为马尔可夫链的统计确认问题.

由给定的转移速率矩阵推导出在某一状态或几个状态下的击中时间的概率密度函数是相对容易的.然而, 使用这些概率密度函数反过来(或逆过程, 或反演)确认潜在的转移速率矩阵是非常困难的, 这是由概率密度函数产生的复杂性(由转移速率经过复杂的运算而产生)造成的.文献[7]提供了一个由观测数据获得转移速率矩阵的办法, 即找出偏差矩阵的Drazin逆, 但它要知道每个状态的平均击中时间.显然, 在实际应用中, 要获得全部状态的击中时间分布是不可能的.因此, 确认问题通常使用极大似然估计方法, 见文献[5, 21, 25, 28, 32]等.此外, 文献[8]开始了探索利用整数集上简单马尔可夫链和两个子集的首次击中时和首次击中位置的联合分布来确定的D-perturbation马尔可夫链的转移概率.

然而, 文献[9, 27-28]提出了马尔可夫链反演方法来执行如此复杂的逆过程, 也称为马尔可夫链的统计确认^[32].该反演过程利用马尔可夫链的潜在拓扑结构这一先验信息, 其关键是禁忌速率对击中时分布性质的进一步揭示和内在编码信息的刻画.这个问题在实际应用中分为三个步骤.我们本文重点关注最后一个关键步骤, 即找出如何通过这些概率密度函数来确认潜在的转移速率矩阵的条件和建议算法.与极大似然法相比, 该方法具有明显的优势, 参见文献[32]以获得更多评论.

保持可逆性的马尔可夫模型的统计确认问题已经讨论了, 其原因已在文献[32]中介绍.事实上, 一些现实系统能够遵循微观可逆性或细致平衡原理, 至少在离子通道的应用中, 可逆性的假设在许多情况下是合理的, 参见文献[23].如何判断是否可逆呢?文献[22]表明可通过环流分解进行判断; 另外, 作为例子, 文献[2, 18]根据两状态轨迹的粗粒度信息(coarsegrained information), 提出了一个判断三状态马尔可夫系统是否可逆的标准.

一般来说, 作为有限状态的可逆马尔可夫链模型, 只有两类拓扑(有环和无环).文献[9, 27-28]提出了生灭链、星形链、星形分枝链等基本的(无环)模型的统计确认方法:生灭链可由任意一个反射壁的观测确认、星形链可由其中心状态的观测确认、星形分枝链可由各分枝的末端(叶子)状态的观测确认.最近, 又解决了更一般的树形马尔可夫链的统计确认问题^[32]:可由所有叶子状态的观测确认; 因为无环的结构类形都属于树形, 因而是一个重要的类型.马尔可夫链统计确认的一个关键问题是找出更一般类型的可行的解决办法并提出建议的算法.因此, 本文将借助禁忌速率探讨最重要并且最关键的另一类型, 即有环(至少包含一个环)的可逆马尔可夫链.得到了确认其转移速率矩阵的必要条件(包括环形的充分必要条件), 以及关于其充分性的一般结论:有环可逆马尔可夫链的转移速率矩阵可以通过所有叶子状态和每个子环中任何两个相邻状态的击中时分布来计算得到; 给出了精确计算各转移速率的算法, 并通过数例验证了算法的正确性.随着无环和有环的可逆马尔可夫链的统计确认问题可以由此方法计算解决, 标志着马尔可夫链的统计确认问题在可逆性条件下已经形成了较为系统的理论和较为成熟的计算.

定理2.1  对于一般的有限状态空间上的连续时间可逆有环马尔可夫链, 如下结论成立.

(Ⅰ)所有叶子状态的观测是确认无环子图的充分条件, 也是首选的有效方法.

(Ⅱ)两相邻状态的观测是确认一个环或子环的必要条件, 也是非常关键的打开环的方法; 如果它有$ k $个子环, 那么$ k $对来自每个子环的两相邻状态的观测是确认它的必要条件.

定理2.2(充分条件)  对于一般的有限状态空间上的连续时间可逆有环马尔可夫链, 其转移速率矩阵可以通过所有叶子状态和每个环中的任何两相邻状态的观测来确认.

推论2.1(充分必要条件)  对于有限状态空间上的连续时间环形可逆马尔可夫链, 两个相邻状态的观测是确认其转移速率矩阵的充分必要条件.

这里所说的观测, 是指实际应用中由观测得到的相应的击中时和逗留时分布的密度函数, 见3.2节; 涉及多个状态的观测时, 要求它们是可区分的, 参见文献[28, 32]; 所谓的两相邻状态是指它们有直接的非零转移, 一般不是多个环的公共节点状态.有必要指出, 通常所说的有环链, 仍然不包含极端复杂的网络情形, 例如, 全连接网络.

为方便起见, diag$ (\cdots) $表示对角矩阵, $ \top $表示转置, $ {\bf 1} $表示一个单位列向量, 0是一个零矩阵(向量), 其维数由上下文确定; $ A_i $表示矩阵的第$ i $列, 并且约定: $ \inf\varnothing = +\infty $.

设$ \{X_t:t\geq0\} $是有限状态空间$ S = \{0, 1, \cdots, M\} $上的连续时间不可约马尔可夫链, 其保守的$ Q $ -矩阵为$ Q = {(q_{ij})}_{S\times S} $, 使得$ Q{\bf 1} = 0\ (q_{ij}\geq 0, j\neq i, q_{i} = -q_{ii}>0), $且$ \widetilde{\pi} = [\pi_0, \pi_{1}, \cdots, \pi_{M}]^{\top} $是$ Q $的平稳分布, 满足

(3.1) $ \begin{equation} \begin{array}{lll} &\widetilde{\pi}^{\top}{\bf 1} = 1, \\ &\widetilde{\pi}^{\top}Q = {\bf 0}. \end{array} \end{equation} $

如果其潜在的马尔可夫链是可逆的, 则其平稳分布满足^{[3-4, 15, 22]}

(3.2) $ \begin{equation} \pi_{i}q_{ij} = \pi_{j}q_{ji}, \forall i, j\in S. \end{equation} $

记$ \Pi\equiv {\rm diag}(\pi_0, \pi_{1}, \cdots, \pi_{M}) $, 则它具有如下的矩阵形式

(3.3) $ \begin{equation} \Pi^{1/2}Q\Pi^{-1/2} = (\Pi^{1/2}Q\Pi^{-1/2})^{\top}. \end{equation} $

如果不特别说明, 本文所说的马尔可夫链通常指有限状态空间上的连续时间可逆马尔可夫链, 且其初始分布是其平稳分布.

设$ O $是状态空间中某些被观测的状态集合, 且满足可区分性条件, 见文献[32], 其他状态表示为$ C = S-O $, 那么可以将Q矩阵写成如下的分块矩阵

(3.4) $ \begin{equation} Q = \left(\begin{array}{ccc} Q_{oo} {\quad}& Q_{oc}\\ Q_{co} {\quad}& Q_{cc} \end{array}\right). \end{equation} $

相应地, 其平稳分布为$ \widetilde{\pi}^{\top} = [\widetilde{\pi}^{\top}_{o}, \widetilde{\pi}^{\top}_{c}] $.

$ O $的击中时(相应地, 逗留时)可定义为$ \tau = \inf\{t>0, X_t\in O\} $ (相应地, $ \sigma = \inf\{t>0, $$ X_t\not\in O\} $), 也称为$ C $的逗留时(相应地, 击中时).

因为需要, 先回顾一下有关聚合马尔可夫链的基本结果.

为了记号简便, 令$ C\equiv\{1, 2, \cdots, N\} $, $ \Pi_c\equiv {\rm diag}(\pi_{1}, \pi_{2}, \cdots, \pi_{N}) $.因为$ Q_{cc} $是非奇异的, 所以它有$ N $个负的特征值, 记为$ -\alpha_{1}, -\alpha_{2}, \cdots, -\alpha_{N}, {(\alpha_{i}>0)} $, 通过在$ (\cdot, \cdot)_{\Pi_c} $下的对称参数化, 可将$ Q_{cc} $进行对角化处理, 相应的正交矩阵为$ E $, 令$ W = \Pi^{-1/2}_c E $, $ D = W^{-1} $, $ A = {\rm diag}(\alpha_1, \alpha_2, \cdots, \alpha_N) $, 可得关于其击中时分布的如下引理^{[28, 32]}.

引理3.1  $ O $的击中时$ \tau $ (相应地, $ C $的逗留时)的概率密度函数服从$ N $ -混合指数密度

$ f_{\tau}(t) = (\widetilde{\pi}^{\top}_{c}{\bf 1})^{-1}(D{\bf 1})^{\top}A\exp(-At)D{\bf 1} = \sum\limits_{i = 1}^{N}\gamma_i\exp(-\alpha_it), \ t>0, $

其中$ \gamma_i = \alpha_i(D{\bf 1})^{\top}_i(D{\bf 1})_i(\widetilde{\pi}^{\top}_{c}{\bf 1})^{-1} $.

推论3.1  单个状态$ i $的逗留时$ \sigma $服从参数为$ q_{i} $的指数分布

$ f_{\sigma}(t) = q_i\exp(-q_it), \ t>0. $

对$ n\geq 1 $, 令

(3.5) $ \begin{equation} d_n = \sum\limits_{i = 1}^{N}{\gamma_i}{\alpha_i^{n-1}}, \quad c_n = (\pi^{\top}_{c}{\bf 1})d_n = (1-\pi^{\top}_{o}{\bf 1})d_n, \end{equation} $

则$ (-1)^{n}d_n $是$ O $的击中时分布函数在零时刻的$ n $阶微分.由系3.1和(2.5)式, 可得如下引理.

引理3.2  设单个状态$ i $的平均逗留时间为$ E\sigma $, 则$ q_i $和$ \pi_i $可由下式得出

(3.6) $ \begin{equation} q_i = 1/E\sigma, \quad \pi_i = d_1/(q_i+d_1) = c_1E\sigma. \end{equation} $

由文献[28, 32]的讨论知, 一旦拟合出基于$ O $观测得到的必要的概率密度函数, 那么相应的$ c_n $$ (n\geq 1) $就是已知常数了.因此, 在后续文中说到"通过某个状态(集)的观测"就是指"通过某个状态(集)的击中时和逗留时的概率密度函数".

击中时分布在零时刻的各阶微分与Q矩阵之间的关系可得一类非常重要的约束关系.

引理3.3  基于观测$ O $的如下微分关系成立

(3.7) $ \begin{equation} c_n = (-1)^{n}{\bf 1}^{\top}\Pi_c Q^n_{cc}{\bf 1}. \end{equation} $

右式虽表达简洁, 但无法直接呈现其实际的构成, 因此, 还需借助禁忌速率进行深入剖析.

对于$ H\subset S $, $ n\in \bf{N} $, 令

(3.8) $ \begin{equation} _H {\bar{q}_{ij}}^{(n)} = \sum\limits_{k_1, \cdots, k_{n-1}\notin H}q_{i, k_{1}}q_{k_{1}k_{2}}\cdots q_{k_{n-1}, j}, i, j\in S, n\geq1 \end{equation} $

为从状态$ i $出发经$ n $步到达状态$ j $, 且在此之前从未到过$ H $的禁忌速率^[29], 则对于给定的$ m = 0, 1, 2, \cdots, n $, 禁忌速率满足如下的Chapman-Kolmogorov (C-K)方程

(3.9) $ \begin{equation} _{H}\overline{q}^{(n)}_{ij} = \sum\limits_{k\notin H}\ _{H}\overline{q}^{(m)}_{ik}\ _{H}\overline{q}^{(n-m)}_{kj}, \end{equation} $

为了更好的理解后续的求解过程, 进一步探索$ _{\{i\}}\overline{q}^{(n)}_{jj} $(从状态$ i $出发经$ n $步回到状态$ i $, 且在此之前从未到过$ H $的禁忌速率)的表达式.

对于给定的$ i, j\in S $, 如果$ q_{ij}>0 $, 称$ i $直接可达$ j $, 记为$ i\rightarrow j $; 称$ i $可达$ j $, 记为$ i\rightsquigarrow j $, 如果存在$ j_1, j_2, \cdots, j_{n-1} \in S $, 使得

$ i\rightarrow j_1\rightarrow j_2\rightarrow \cdots \rightarrow j_{n-1}\rightarrow j. $

令$ L(i, j;n) = (i, j_{1}, \cdots, j_{n-1}, j) $为从状态$ i $到达状态$ j $的一个路径, 这里, $ n $表示路径长度.进一步, 称$ i $和$ j $是互通的, 如果$ q_{ij}>0 $且$ q_{ji}>0 $, 记为$ i\leftrightarrow j $.因此, 对于可逆马尔可夫链来说, $ i\rightarrow j $意味着$ i\leftrightarrow j $.与状态$ i $直接可达的状态的数目称为状态$ i $的节点度数, 记为$ \deg(i) $; 如果一个状态$ i $的度数$ \deg(i) = 1 $, 则称为叶子状态.

$ _ {H}\overline{q}^{(n)}_{jj} $从$ j $出发, 经过$ n $步转移后再要回到$ j $, 一般情况下, 它最多只能跑到距离它$ n/2 $步的状态, 所以, 对于给出的$ j\in S $, $ n\in N^{+} $, 互不相同的$ j, j_1, \cdots, j_m\notin H $ ($ 1\leq m\leq [\frac{n}{2}] $), 我们用禁忌速率$ _ {H}\overline{q}^{(n)}_{jj}(j\leftrightarrow j_1\leftrightarrow \cdots\leftrightarrow j_{m}) $表示从状态$ j $出发, 沿着路径$ L(j, j_m;m) = (j, j_1, \cdots, j_m) $, 最远到达$ j_m $, 然后回到状态$ j $的速率.

性质3.1  令$ \overline{q}(j_1, j_2, \cdots j_k) = q_{j_1, j_2}q_{j_2, j_3}\cdots q_{j_{k-1}, j_k}q_{j_{k}, j_{k-1}}\cdots q_{j_3, j_2}q_{j_2, j_1}, \!\! $下列等式成立^[29]

(3.10) $ \begin{eqnarray} _{\{i\}}\overline{q}^{(2k+1)}_{jj} (j\leftrightarrow j_1\leftrightarrow \cdots\leftrightarrow j_{k})& = &\bigg({\bf q}_{j_{k}}+2\sum\limits_{s\in \{j, j_1, \cdots, j_{k-1}\}}q_{s}\bigg)\ \overline{q}(j, j_1, \cdots, j_k){}\\ &&+ _{\{i\}}\overline{q}^{(2k+1)}_{jj}(j\leftrightarrow j_1\leftrightarrow \cdots\leftrightarrow j_{k-1}), \\ _{\{i\}}\overline{q}^{(2k+2)}_{jj}(j\leftrightarrow j_1\leftrightarrow \cdots\leftrightarrow j_{k+1})& = & q_{j_k, j_{k+1}}{{\bf q}_{j_{k+1}, j_k}}\ \overline{q}(j, j_1, \cdots, j_k){}\\ &&+_{\{i\}}\overline{q}^{(2k+2)}_{jj}(j\leftrightarrow j_1\leftrightarrow \cdots\leftrightarrow j_{k}).{} \end{eqnarray} $

在后面的求解过程中, 每个公式中粗体字的量可能是其中的一个新的未知量.

推论3.2  $ O $的微分关系可用禁忌速率表达成^[29]

(3.11) $ \begin{equation} c_n = (-1)^{n+1}\sum\limits_{j\in O}\sum\limits_{i\in C}\pi_i\ _{O}\overline{q}^{(n)}_{ij} = (-1)^{n+1}\sum\limits_{j\in O}\pi_j\sum\limits_{i\in C}\ _{O}\overline{q}^{(n)}_{ji}. \end{equation} $

特别地, 若$ O = \{i\} $, 则推论3.2为

推论3.3  如果单个状态$ i $在一个树(或$ m $个状态的环)中, 那么关于$ i $的微分关系能够解码为如下形式, 对所有的$ n $ (或$ n<m $), 有

(3.12) $ \begin{eqnarray} c_1& = &\pi_i\sum\limits_{j}\ _{\{i\}}\overline{q}^{(1)}_{ij} = \sum\limits_{j\neq i}\pi_iq_{ij} = \sum\limits_{j\neq i}\pi_jq_{ji}, {}\\ c_2& = &\pi_i\ _{\{i\}}\overline{q}^{(2)}_{ii} = \sum\limits_{j\neq i}\pi_iq_{ij}q_{ji} = \sum\limits_{j\neq i}\pi_j (q_{ji})^2, {}\\ c_3& = &\pi_i\ _{\{i\}}\overline{q}^{(3)}_{ii} = \sum\limits_{j\neq i}\pi_iq_{ij}\ _{\{i\}}\overline{q}^{(1)}_{jj}q_{ji} = \sum\limits_{j\neq i}\pi_iq_{ij}q_jq_{ji} = \sum\limits_{j\neq i}\pi_j (q_{ji})^2q_j, \\ c_4& = &\pi_i\ _{\{i\}}\overline{q}^{(4)}_{ii} = \sum\limits_{j\neq i}\pi_iq_{ij}\ _{\{i\}}\overline{q}^{(2)}_{jj}q_{ji} = \sum\limits_{j\neq i}\pi_iq_{ij}\bigg[\sum\limits_{k\neq i}q_{jk}q_{kj}\bigg]q_{ji}{}\\ & = &\sum\limits_{j\neq i}\pi_j(q_{ji})^2\bigg[\sum\limits_{k\neq i}q_{jk}q_{kj}\bigg], {}\\ c_{n}& = &\pi_i\ _{\{i\}}\overline{q}^{(n)}_{ii} = \sum\limits_{j\neq i}\pi_iq_{ij}\ _{\{i\}} \overline{q}^{(n-2)}_{jj}q_{ji} = \sum\limits_{j\neq i}\pi_j(q_{ji})^2\ _{\{i\}}\overline{q}^{(n-2)}_{jj}, n\geq 5.{} \end{eqnarray} $

右边第一个方程就是状态$ i $的所有流出(或流入)速率的和.这里为了记号简洁, 让$ q_{kk} = q_k $, 即可去掉$ c_n $右边前面的系数$ (-1)^n $.

上述可能的转移解码了$ Q_{cc} $和$ c_n $之间的信息, 使得大部分的转移都可由$ c_n $求解出.为了求解过程的简单和计算的精确性, 通常叶子状态观测是首选.

最后, 适当放宽^[32]中有关可确定性的条件(主要考虑完全树或状态数很少的特殊的环的情形), 对马氏链的统计确认施加了一个相对温和的限制条件, 即所观测的状态数至多比整个链状态数的一半多一个时, 从马尔可夫链统计确认的意义上来说, 称为可确定的.

定理2.1(Ⅰ)来自树形马尔可夫链的统计确认理论^[32]:可由所有叶子状态的观测确认.

关于定理2.1(Ⅱ).首先, 根据生灭链^[9]及后续的研究, 如果只观测一个不是反射壁的状态时, 它是无法确定该生灭链的, 从而更无法确定一个环形链或子环.因此, 要确定一个环形链, 至少需要观测两个状态, 而且, 如果两个状态不相邻的话, 也无法确定该环形链, 即使观测链中一半的互不相邻的状态, 也无法确定; 例如, 环中共有$ 2N $个状态, 记为$ 1, 2, \cdots, 2N $, 即使我们观测状态$ 1, 3, 5, 7, \cdots, 2N-1 $, 也无法找到打开环的突破口, 也就无法求出其转移速率矩阵.也就是说, 要打开一个环, 两相邻状态的观测是必要条件.

同理, 如果一个链中有$ k $个环(指最小的环, 例如, 图 5中只能算两个环), 那么每个环都需要两个相邻状态的观测才能独立的打开, 从而需要观测$ k $对两相邻的状态.

因此, 定理2.1成立.

环形链是指由仅仅只有一个环的链.给定一个有限状态空间$ S = \{1, 2, \cdots, N\} $上的环形马尔可夫链, 即每个状态只与其他相邻的状态是互通的, 其中$ N $和$ 1 $是互通的.

与对应的生灭链相比, 其中只是多了$ q_{1N} $和$ q_{N1} $这两个非零的转移速率.另外, 可逆性要求满足$ q_{12}\cdots q_{N-1, N}q_{N1} = q_{N, N-1}\cdots q_{21}q_{1N} $, 即文献[23]中所说的满足微观可逆性或通道中的细致平衡条件.这两个链之间的转移速率的差异看起来可能不是很明显, 但其动力学行为却有很大的不同.因此, 它非常重要, 而且要确定其转移速率的难度急剧增加.

引理5.1  对于$ O = \{m, m+1\}\ (1\leq m, m+1\leq N) $来说, 下列方程成立.

(5.1) $ \begin{equation} c^{(m, m+1)}_1 = \pi_mq_{m, m-1}+\pi_{m+1}q_{m+1, m+2}, \end{equation} $

(5.2) $ \begin{equation} c^{(m, m+1)}_2 = \pi_mq^2_{m, m-1}+\pi_{m+1}q^2_{m+1, m+2}. \end{equation} $

下面的引理可由推论3.3得出.

引理5.2  接下来的方程对任意的$ 1\leq i\leq N $, 和$ 2\leq s\leq [\frac{N-1}{2}] $成立.

(5.3) $ \begin{equation} \frac{1}{E\sigma^{(i)}} = q_i = q_{i, i+1}+q_{i, i-1}, \end{equation} $

(5.4) $ \begin{equation} c^{(i)}_1 = \pi_{i-1}q_{i-1, i}+\pi_{i+1}q_{i+1, i}, \end{equation} $

(5.5) $ \begin{equation} c^{(i)}_2 = \pi_{i-1}q^2_{i-1, i}+\pi_{i+1}q^2_{i+1, i}, \end{equation} $

(5.6) $ \begin{equation} c^{(i)}_3 = \pi_{i-1}q^2_{i-1, i}\ {{\bf q}_{i-1}}+\pi_{i+1}q^2_{i+1, i}\ q_{i+1}, \end{equation} $

(5.7) $ \begin{equation} c^{(i)}_4 = \pi_{i-1}q^2_{i-1, i}(q^2_{i-1}+q_{i-1, i-2}\ {{\bf q}_{i-2, i-1}})+\pi_{i+1}q^2_{i+1, i}(q^2_{i+1}+q_{i+1, i+2}\ q_{i+2, i+1}), \end{equation} $

(5.8) $ \begin{eqnarray} c^{(i)}_{2s+1}& = &\pi_{i-1}q^2_{i-1, i}\big[({{\bf q}_{i-s}}+2\sum\limits^{s-1}_{k = 1}q_{i-k})\ \overline{q}(i-1, i-2, \cdots, i-s){}\\ &&+ _{\{i\}}\overline{q}^{(2s-1)}_{i-1, i-1}(i-1\leftrightarrow i-2\leftrightarrow \cdots\leftrightarrow i-s+1)\big]{}\\ & &+\pi_{i+1}q^2_{i+1, i}\big[({{\bf q}_{i+s}}+2\sum\limits^{s-1}_{k = 1}q_{i+k})\ \overline{q}(i+1, i+2, \cdots, i+s){}\\ &&+ _{\{i\}}\overline{q}^{(2s-1)}_{i+1, i+1}(i+1\leftrightarrow i+2\leftrightarrow \cdots\leftrightarrow i+s-1)\big], \end{eqnarray} $

(5.9) $ \begin{eqnarray} c^{(i)}_{2s+2}& = &\pi_{i-1}q^2_{i-1, i}[q_{i-s, i-s-1}{{\bf q}_{i-s-1, i-s}}\ \overline{q}(i-1, i-2, \cdots, i-s){}\\ &&+_{\{i\}}\overline{q}^{(2s)}_{i-1, i-1}(i-1\leftrightarrow i-2\leftrightarrow \cdots\leftrightarrow i-s)]{}\\ & &+\pi_{i+1}q^2_{i+1, i}[q_{i+s, i+s+1}{{\bf q}_{i+s+1, i+s}}\ \overline{q}(i+1, i+2, \cdots, i+s){}\\ &&+_{\{i\}}\overline{q}^{(2s)}_{i+1, i+1}(i+1\leftrightarrow i+2\leftrightarrow \cdots\leftrightarrow i+s)]. \end{eqnarray} $

其中对于$ i+s>N $, 有$ i+s\doteq (i+s)-N $且对于$ i-s\leq 0 $有$ i-s\doteq (i-s)+N $, 下同.

(5.8)式或(5.9)式的右边表明仅有黑体部分的两个可能是较前一阶导数新增的未知量.然而, 在后续通过确定的两相邻状态的观测来求解的过程中, 每个方程都只有一个新的未知速率, 具体地说, 当观测两个相邻状态中较小(相应地, 较大)的状态时, 只有第一个(相应地, 第二个)黑体是未知量；例如, 如果观测状态为$ m $和$ m+1 $, 则$ c^{(m)}_{n} $中的第一个是新的未知量, $ c^{(m+1)}_{n} $中的第二个是新的未知量.

推论2.1的证明  由定理2.1(Ⅰ), 要证明推论2.1, 只需要证明两相邻状态的观测也是充分条件即可, 即证明：对于环形链, 由其中任意两相邻状态的观测可确认全部转移速率.

不失一般性, 设$ m $和$ m+1 $$ (1\leq m, m+1\leq N) $是观测的两相邻状态.

首先, 环是可打开的.根据(5.3)式, 对于$ i = m $和$ i = m+1 $有$ q_i = 1/E\sigma^{(i)}, \pi_i = c^{(i)}_1E\sigma^{(i)} $.则$ q_{m, m-1} $和$ q_{m+1, m+2} $是方程(5.1)–(5.2)的两个实根, 这两个实根也是关于$ c^{(m, m+1)}_n $$ (n = 1, 2) $和$ c^{(m)}_1, c^{(m+1)}_1 $的实函数.于是有$ q_{m, m+1} = q_m-q_{m, m-1} $和$ q_{m+1, m} = q_{m+1}-q_{m+1, m+2} $成立.

其次, 当$ i = m $和$ i = m+1 $时, 分别可得$ \pi_{m-1}, q_{m-1, m} $和$ \pi_{m+2}, q_{m+2, m+1} $是方程(5.6)–(5.7)的两个实根.

(5.10) $ \begin{equation} \label{eq-cycle-1} \begin{array}{lll} { } q_{m-1} = \frac{c^{(m)}_3-\pi_{m+1}q^2_{m+1, m}q_{m+1}}{\pi_{m-1}q^2_{m-1, m}}, \quad { } q_{m+2} = \frac{c^{(m+1)}_3-\pi_{m}q^2_{m, m+1}q_m}{\pi_{m+2}q^2_{m+2, m+1}}, {\nonumber}\\ [2mm] { } q_{m-1, m-2} = q_{m-1}-q_{m-1, m}, q_{m+2, m+3} = q_{m+2}-q_{m+2, m+1}. \end{array} \end{equation} $

进一步, 当$ i = m, m+1 $时, 根据(5.7)式可得

(5.11) $ \begin{eqnarray} &&q_{m-2, m-1} = \frac{c^{(m)}_4-\pi_{m+1}q^2_{m+1, m}(q^2_{m+1}+q_{m+1, m+2}\ q_{m+2, m+1})-\pi_{m-1}q^2_{m-1, m}q^2_{m-1}}{\pi_{m-1}q^2_{m-1, m}q_{m-1, m-2}}, {}\\ &&q_{m+3, m+2} = \frac{c^{(m+1)}_4-\pi_{m}q^2_{m, m+1}(q^2_{m}+q_{m, m-1}q_{m-1, m})-\pi_{m+2}q^2_{m+2, m+1}q^2_{m+2}}{\pi_{m+2}q^2_{m+2, m+1}q_{m+2, m+3}}, \\ &&\pi_{m-2} = \frac{\pi_{m-1}q_{m-1, m-2}}{q_{m-2, m-1}}, \quad \pi_{m+3} = \frac{\pi_{m+2}q_{m+2, m+3}}{q_{m+3, m+2}}. {} \end{eqnarray} $

这意味着当$ i = m $ (或$ i = m+1 $)时, 根据(5.8)式可以向左(或向右)移动得到$ q_{m-s} $和$ q_{m-s, m-s-1} = q_{m-s}-q_{m-s, m-s+1} $ (或$ q_{m+s+1} $和$ q_{m+s+1, m+s+2} = q_{m+s+1}-q_{m+s+1, m+s} $), 于是, 当$ i = m $ (或$ i = m+1 $)时, 也可以根据(5.9)式向左(或向右)移动得到$ q_{m-s-1, m-s} $ (或$ q_{m+s+2, m+s+1} $).

最后, 可用数学归纳法来证明该推论, 这里省略繁琐的证明细节.因此, 两相邻状态的观测是确认一个环形链的充分必要条件, 即先通过任意两个相邻状态的观测打开环, 然后前后(向左和向右)依次确认其余的转移速率, 这也是有环链的统计确认的一个关键思想.

注5.1  这个简要的证明思路给出了相应的算法.文献[31]通过观测两个特殊的相邻状态给出了另一个更具体的证明和算法.需要指出的是, 虽然文献[31]表明了$ c_n $是关于某些转移速率的函数表达, 但仍不清楚其构成; 而本文关于$ c_n $的表达式比文献[31]中的更清晰, 可以明确地看出每个$ c_n $的构成, 甚至可以说, 能够准确地写出每个表达式.

算法5.1  环形链.

1) 打开环:根据证明中的第一部分可以计算出$ q_m, q_{m+1}, \pi_m, \pi_{m+1} $, $ q_{m, m-1} $和$ q_{m+1, m+2} $, $ q_{m, m+1} $和$ q_{m+1, m} $;

2) 根据(5.4)和(5.5)式, 向左计算出$ \pi_{m-1}, q_{m-1, m} $, 向右计算出$ \pi_{m+2}, q_{m+2, m+1} $;

3) 根据(5.10)式, 向左计算出$ q_{m-1}, q_{m-1, m-2} $, 向右计算出$ q_{m+2}, q_{m+2, m+3} $;

4) 根据(5.11)式, 向左计算出$ q_{m-2, m-1}, \pi_{m-2} $, 向右计算出$ q_{m+3, m+2}, \pi_{m+3} $;

5) 重复步骤3)和步骤4):对于$ s = 2, 3, \cdots $, 根据(5.4)和(5.5)式分别向左和向右可以计算出剩余的转移速率.

本文说单环链是指由一个环和其他无环的子图组成的链；有环的链是指至少有一个环的链.不失一般性, 考虑具有代表性的单环链(环形链是特例)和双环链.解决了这些代表性的有环链的统计确认, 对于一般的有环的马尔可夫链, 只当作是它们的组合, 也就自然证明了定理2.2是成立的.

首先, 考虑一条直线连接的单环链, 类似于环形链的情形, 可逆性要求其转移速率满足$ q_{12}\cdots q_{N-1, N}q_{N1} = q_{N, N-1}\cdots q_{21}q_{1N} $.文献[23]中列举了图 1特例(直线上仅有1个状态)的离子通道门控, 其实还有许多一条直线连接的单环图, 如蝌蚪图和平锅图.文献[25, 30]研讨了这一类中最简单的情形(即环中仅有3个状态且直线上仅有1个状态)的解决方案.

$ \begin{array}{ccccccccccccccccccccc} &0&\rightleftharpoons&\cdots&\rightleftharpoons&1&\rightleftharpoons&N\\ &&&&&\upharpoonleft\downharpoonright& &\vdots\\ &&&&&2&\rightleftharpoons&3 \end{array} $

根据线性子图的结果, 通过状态$ 0 $的逗留时间和击中时间的概率密度函数可以确认$ 0 $和$ 1 $之间所有转移速率.根据环形链的求解方法, 不难得到一个关于充分性的结果如下.

定理6.1  对于图 1中的马尔可夫链, 可以通过叶子状态和环中任意两相邻状态的观测确认.

证明很简单.相应的算法就是先直接根据文献[9]中生灭连的算法计算出线性子图的转移速率, 然后根据算法5.1计算子环中的其它转移速率.实际上, 还可以给出一个更优的结论.

定理6.2  对于图 1中的马尔可夫链, 它可以通过环中任意两相邻状态(除了度数为$ 3 $的状态)的观测来确认.

证  根据环形链统计确认的基本思想, 观测距离节点度数为$ 3 $的状态(即图 1中的状态$ 1 $)越远的两个邻接状态时, 特别是当两邻接状态是子环的中心状态时, 就越容易确定子环中的转移速率.不失一般性, 类似于前一小节中的环形链的证明, 两相邻的状态$ m $和$ m+1 $使得$ m-2\leq N-(m+1) $.为了方便表达, 令$ 1' , 2' , \cdots, M' $是右图中状态$ 0 $和$ 1 $之间从左到右的状态编号.

该证明与环形链的证明思路几乎是一样的, 主要变化是关于$ m $和$ m+1 $的(6.1)–(6.2)式中多出的两个表达式的替换.首先, 对于$ \{m, m+1\} $有(5.1)–(5.2)式成立, 且对于$ i = m $和$ i = m+1 $分别有(5.3)–(5.6)式成立.可以按前一小节中的环形链类似的方法打开图 1中的子环.

第二, 当$ s\leq m-2 $时, (5.8)–(5.9)式分别对$ i = m $和$ i = m+1 $成立.因此, 根据环形链的算法, 从状态$ m $ (或$ m+1 $)可以向左(或向右)确认出状态$ m-j $ (或$ m+1+j $)的转移速率(即$ j = 0, 1, 2, \cdots, m-1 $), 直到$ m-j = 1 $的转移速率.也就是说, 直到$ s = m-2 $, 可以得到从状态$ 1 $到$ 2m $之间的所有转移速率.

第三, 当$ N-m+1\geq s\geq m-1 $时, 对于$ i = m $来说, (5.8)–(5.9)式更新如下.

(6.1) $ \begin{equation} c^{(m)}_{2s+1} = \pi_{m-1}q^2_{m-1, m}\big[A^{s}_1+A^{s}_2+A^{s}_3+A^{s}_4\big]+\pi_{m+1}q^2_{m+1, m}\big[B^{s}_1+B^{s}_2\big ], \end{equation} $

其中

$ A^{s}_1 = ({\bf q}_{(s-m+1)' }+2\sum\limits^{m-1}_{k = 1}q_k+2\sum\limits^{s-m}_{k = 1}q_{k' })\ \overline{q}(m-1, \cdots , 2, 1, 1' , 2' , \cdots, (s-m+1)' ), $

$ A^{s}_2 = _{\{m\}}\overline{q}^{(2s-1)}_{m-1, m-1}(m-1\leftrightarrow \cdots\leftrightarrow 2\leftrightarrow 1\leftrightarrow 1' \leftrightarrow 2' \leftrightarrow \cdots\leftrightarrow (s-m)' ), $

$ A^{s}_3 = {(\bf q}_{m-s+N}+2\sum\limits^{s-1}_{k = 1}q_{m-k})\ \overline{q}(m-1, \cdots, 2, 1, N, N-1, \cdots, N-s+m), $

$ A^{s}_4 = _{\{m\}}\overline{q}^{(2s-1)}_{m-1, m-1}(m-1\leftrightarrow \cdots\leftrightarrow 2\leftrightarrow 1\leftrightarrow N\leftrightarrow N-1\leftrightarrow \cdots\leftrightarrow N-s+m+1), $

$ B^{s}_1 = ({\bf q}_{m+s}+2\sum\limits^{s-1}_{k = 1}q_{m+k})\ \overline{q}(m+1, m+2, \cdots, m+s), $

$ B^{s}_2 = _{\{m\}}\overline{q}^{(2s-1)}_{m+1, m+1}(m+1\leftrightarrow m+2\leftrightarrow \cdots\leftrightarrow m+s-1); $

(6.2) $ \begin{equation} c^{(m)}_{2s+2} = \pi_{m-1}q^2_{m-1, m}\big[A^{s}_5+A^{s}_6+A^{s}_7+A^{s}_8\big]+\pi_{m+1}q^2_{m+1, m}\big[B^{s}_3+B^{s}_4\big]. \end{equation} $

其中

$ A^{s}_5 = q_{(s-m+1)' , (s-m+2)' }{{\bf q}_{(s-m+2)' , (s-m+1)' }}\overline{q}(m-1, \cdots, 2, 1, 1' , \cdots, (s-m+1)' ), $

$ A^{s}_6 = _{\{m\}}\overline{q}^{(2s)}_{m-1, m-1}(m-1\leftrightarrow m-2\leftrightarrow \cdots\leftrightarrow 1\leftrightarrow 1' \leftrightarrow 2' \leftrightarrow \cdots\leftrightarrow (s-m+1)' ), $

$ A^{s}_7 = {q_{N-s+m-1, N-s+m}{\bf q}_{N-s+m, N-s+m-1}}\ \overline{q}(m-1, \cdots, 1, N, \cdots, N-s+m), $

$ A^{s}_8 = _{\{m\}}\overline{q}^{(2s)}_{m-1, m-1}(m-1\leftrightarrow m-2\leftrightarrow \cdots\leftrightarrow 1\leftrightarrow N\leftrightarrow N-1\leftrightarrow \cdots\leftrightarrow N-s+m), $

$ B^{s}_3 = q_{m+s, m+s+1}{{\bf q}_{m+s+1, m+s}}\ \overline{q}(m+1, m+2, \cdots, m+s), $

$ B^{s}_4 = _{\{m\}}\overline{q}^{(2s)}_{m+1, m+1}(m+1\leftrightarrow m+2\leftrightarrow \cdots\leftrightarrow m+s), $

通过比较(5.8)–(5.9)式与(6.1)–(6.2)式, 可以发现主要变化是$ A^{s}_j $ ($ j = 1, 2, 5, 6 $)中多出了状态$ 0 $到$ 1 $之间的未知速率.然而, 在下面关于$ i = m+1 $的方程中, 它们也会出现在相同的部分.

(6.3) $ \begin{eqnarray} c^{(m+1)}_{2s+3}& = &\pi_{m}q^2_{m, m+1}\ _{\{m+1\}}\overline{q}^{(2s+1)}_{m, m} +\pi_{m+2}q^2_{m+2, m+1}\ _{\{m+1\}}\overline{q}^{(2s+1)}_{m+2, m+2}{}\\ & = &\pi_{m}q^2_{m, m+1}q_{m, m-1}q_{m-1, m}\big[A^{s}_1+\overline{A}^{s}_2+A^{s}_3+\overline{A}^{s}_4\big] +\pi_{m+2}q^2_{m+2, m+1}\big[\overline{B}^{s}_1+\overline{B}^{s}_2\big], {\qquad} \end{eqnarray} $

其中

$ \overline{A}^{s}_2 = _{\{m+1\}}\overline{q}^{(2s-1)}_{m-1, m-1}(m-1\leftrightarrow \cdots\leftrightarrow 2\leftrightarrow 1\leftrightarrow 1' \leftrightarrow 2' \leftrightarrow \cdots\leftrightarrow (s-m)' ), $

$ \overline{A}^{s}_4 = _{\{m+1\}}\overline{q}^{(2s-1)}_{m-1, m-1}(m-1\leftrightarrow \cdots\leftrightarrow 1\leftrightarrow N\leftrightarrow N-1\leftrightarrow \cdots\leftrightarrow N-s+m+1), $

$ \overline{B}^{s}_1 = ({{\bf q}_{m+s+2}}+2\sum\limits^{s+1}_{k = 2}q_{m+k})\ \overline{q}(m+2, m+3, \cdots, m+s+2), $

$ \overline{B}^{s}_2 = _{\{m+1\}}\overline{q}^{(2s+1)}_{m+2, m+2}(m+2\leftrightarrow m+3\leftrightarrow \cdots\leftrightarrow m+s+2); $

(6.4) $ \begin{eqnarray} c^{(m+1)}_{2s+4}& = &\pi_{m}q^2_{m, m+1}\ _{\{m+1\}}\overline{q}^{(2s+2)}_{m, m}+\pi_{m+2}q^2_{m+2, m+1}\ _{\{m+1\}}\overline{q}^{(2s+2)}_{m+2, m+2}{}\\ & = &\pi_{m}q^2_{m, m+1}q_{m, m-1}q_{m-1, m}\big[A^{s}_5+\overline{A}^{s}_6+A^{s}_7+ \overline{A}^{s}_8\big]+\pi_{m+2}q^2_{m+2, m+1}\big[\overline{B}^{s}_3+\overline{B}^{s}_4\big], {\qquad} \end{eqnarray} $

其中

$ \overline{A}^{s}_6 = \ _{\{m+1\}}\overline{q}^{(2s)}_{m-1, m-1}(m-1\leftrightarrow \cdots\leftrightarrow 1\leftrightarrow 1' \leftrightarrow 2' \leftrightarrow \cdots\leftrightarrow (s-m+1)' ), $

$ \overline{A}^{s}_8 = \ _{\{m+1\}}\overline{q}^{(2s)}_{m-1, m-1}(m-1\leftrightarrow m-2\leftrightarrow \cdots\leftrightarrow 1\leftrightarrow N\leftrightarrow \cdots\leftrightarrow N-s+m), $

$ \overline{B}^{s}_3 = q_{m+s+2, m+s+3}{{\bf q}_{m+s+3, m+s+2}}\ \overline{q}(m+2, m+3, \cdots, m+s+2), $

$ \overline{B}^{s}_4 = _{\{m+1\}}\overline{q}^{(2s+2)}_{m+2, m+2}(m+2\leftrightarrow m+3\leftrightarrow \cdots\leftrightarrow m+s+2). $

注意到以上方程中, 禁忌集合$ \{m\} $和$ \{m+1\} $是等价的, 这表明了$ \overline{A}^{s}_j = A^{s}_j $对$ j = 2, 4, 6, 8 $均成立.因此, 分别把(6.1)–(6.2)式中的$ A^{s}_j $ ($ j = 1, 2, 5, 6 $)替换到(6.3)–(6.4)式中, 就可以进一步确认出状态$ \{2m+1, 2m+2, \cdots, N, 1\} $之间的转移速率.

这表明可以通过从$ m $ (或$ m+1 $)出发同时向左或向右确认转移速率, 直到确认出所有的转移速率.

最后, 返回到(6.1)和(6.2)式中的$ A^{s}_j $ ($ j = 1, 2, 5, 6 $), 我们可以确定从状态$ 1 $到$ 0 $之间(即状态$ \{1, 1' , 2' \cdots, M' , 0\} $)的所有转移速率.

注6.1  如果两相邻状态包含了图中唯一的度数为$ 3 $的状态(即状态$ 1 $), 则无法打开环.

算法6.1  由一个环和一条直线组成的单环链.

1) 根据算法5.1, 打开环并确认出状态$ 1 $到$ 2m $之间的转移速率, 直到$ s = m-2 $, 即$ \pi_j, q_j $, $ q_{j, j+1}, q_{j+1, j}\ j = 1, \cdots, 2m $;

2) 对于$ s = m-1 $来说, 通过把(6.1)式中的$ A^{m-1}_j $ ($ j = 1, 2 $)代入到(6.3)式中, 向右计算出$ q_{2m+1} $; 于是有

$ q_{2m+1, 2m+2} = q_{2m+1}-q_{2m+1, 2m}; $

3) 对于$ s = m-1 $来说, 通过把(6.2)式中的$ A^{m-1}_j $ ($ j = 5, 6 $)代入到(6.4)式中, 向右计算出$ q_{2m+2, 2m+1} $; 于是有

$ \pi_{2m+2} = \pi_{2m+1}q_{2m+1, 2m+2}/q_{m+2, m+1}; $

4) 重复步骤2)和步骤3):计算出状态$ 2m+2 $和$ N $之间的其余转移速率, 即$ \pi_j, q_j, q_{j, j+1}, $$ q_{j+1, j} $ ($ j = 2m+2, \cdots, N $, 且$ q_{N+1, N} = q_{1N}, q_{N, N+1} = q_{N1}) $;

5) 对于$ s = m-1 $, 由(6.1)和(6.2)式计算出$ q_{1' } $与$ q_{1' , 1} $; 于是有

$ q_{1, 1' } = q_{1}-q_{1N}-q_{12}, \ \pi_{1' } = \pi_{1}q_{1, 1' }/q_{1' , 1}, \ q_{1' , 2' } = q_{1' }-q_{1' , 1}-q_{1' , N}; $

6) 重复步骤5):在$ s = m, m+1, \cdots $的情况下, 通过(6.1)与(6.2)式, 沿着直线的部分, 计算出从$ 1' $到$ 0 $的所有转移速率.

接下来, 对含有多条直线的单环链, 例如图 2, 当所有叶子状态可观测时, 可以确定所有直线上的转移速率.于是可得如下结论.

定理6.3  对于图 2中含有多条直线的单环链, 每个链都可以通过所有叶子状态以及环形中任意两相邻状态的观测确认.

对于一般的单环链:树形和环形的组合.作为一个例子, 见图 3.根据树形马尔可夫链的结论^[32], 通过所有叶子状态的观测就可以确认出整个树形子链, 于是可得如下结论.

定理6.4  对于由一个树形和环形组成的单环链, 可以通过树中所有叶子状态和环中任何两相邻状态的观测来确认.

算法6.2  树和环组成的单环链.

1) 由文献[32]中树形链的确认算法, 通过观测所有叶子可以确认出整个树形部分转移速率;

2) 类似于一条直线的单环链的确认算法, 通过观察环中的任何两相邻状态就可以计算子环中的所有转移速率.

注6.2  不是所有叶子状态都需要观测.理论上, 当所有的叶子中只有一个是不可能观测时, 它也是可确认的.然而, 对所有叶子的观测应该是最优的, 这样可以最小化误差传播. \label{remark-cycle-tree}

作为含有多个环的有环链的代表, 首先论证两个环通过一条直线连接的有环链.

图 4由两个环通过一条直线连接的有环链的示意图.如前所述, 需要分别观测左环中的两相邻状态和右环中的另两相邻状态分割打开两个环.因此, 可以得出下面的通过最少的状态观测的结论.

定理6.5  对于图 4中的双环链, 它可以通过左环中的任何两相邻状态和右环中的任何两相邻状态的观测来确认.

证  关键的方法是将两个环分别打开.正如由一条直线的单环链的统计确认理论中所述, 两相邻状态距离节点度数为$ 3 $的状态越远, 越容易确认出该子环的转移速率, 特别是当两个邻接状态是该子环的中心状态时.而且, 应该先确认状态数较少的环.不失一般性, 假设左环内的状态数少于右环内的状态数, 即$ N<M' $.

先考虑左边的子环.类似于前述的环形链的情况, 满足条件$ m-2\leq N-(m+1) $的两相邻状态$ m $和$ m+1 $被观测, 可以确定左子环和线性部分的转移速率.

类似于前面小节中的一条直线的单环链, 可以很容易地打开左边的子环, 然后确定状态$ 1 $和$ 2m $之间的转移速率.在后续的从状态$ 2m+1 $到$ N $之间转移速率的求解过程中, $ c^{(m)}_{n} (n>m) $中不仅包含直线部分的转移速率, 而且包含右边子环中的转移速率.然而, 它们可以用类似于定理6.2中那样, 被$ c^{(m+1)}_{n+2} (n>m) $中的相同部分来代替.进一步可以确认线性部分的转移速率.

再继续通过观测右环的任何两相邻状态来确认其转移速率.

注6.3  以上两个子环中存在两个节点度数为$ 3 $的状态, 即图 4中的状态$ 1 $和状态$ 1' $.如果左环中的两相邻状态包含状态$ 1 $, 且右环中的另两相邻状态包含状态$ 1' $, 则第一步将无法打开任何一个子环.如果两个环中间没有直线的部分, 且共一个节点状态, 比如, 状态$ 1 $和状态$ 1' $重合, 形成一个“8”字形, 此时, 状态$ 1 $是两个环的公共状态, 则该链还可由状态$ 1 $和两个环中与之相邻的各一个状态的观测来确认(例如, $ \{1, 2, 2'\} $).

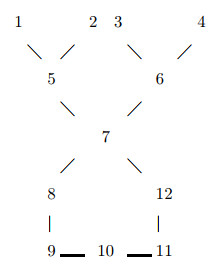
然后, 考虑一个更复杂的情形, 即两个环共一条边的双环链, 如图 5.

定理6.6  对于图 5所示有公共边的双环链, 它可以通过上面环中的任意两相邻状态和下面环中的任意两相邻状态(即$ \{A_1, \cdots, A_m\} $中的任意两相邻状态, $ \{B_2, \cdots, B_{n-1}\} $中的任意两相邻状态, $ \{C_1, \cdots, C_s\} $中的任意两相邻状态, $ 3 $对相邻状态中任选$ 2 $对)的观测来确认.

为了证明该算法的正确性和该方法的统计意义, 本文给出了一个数例.正如前面所述, 本文主要集中在求解的最后一步, 且假定已经很好的拟合出了每个需要观测的状态的逗留时和击中时的概率密度函数.

设$ \{X_t;t\geq 0\} $是一个含有树的单环链(见图 6), 状态空间为$ S = \{1, 2, 3, 4, 5, 6, 7, 8, $$ 9, 10, 11, 12\} $, 转移速率矩阵为\\

(7.1) $ \begin{equation} Q = \left(\begin{array}{cccccccccccc} -10 &0 &0 &0 &10 &0 &0 &0 &0 &0 &0 &0\\ 0 &-25 &0 &0 &25 &0 &0 &0 &0 &0 &0 &0\\ 0 &0 &-30 &0 &0 &30 &0 &0 &0 &0 &0 &0\\ 0 &0 &0 &-15 &0 &15 &0 &0 &0 &0 &0 &0\\ 5 &15 &0 &0 &-50 &0 &30 &0 &0 &0 &0 &0\\ 0 &0 &10 &15 &0 &-40 &15 &0 &0 &0 &0 &0\\ 0 &0 &0 &0 &5 &10 &-50 &10 &0 &0 &0 &50\\ 0 &0 &0 &0 &0 &0 &25 &-75 &50 &0 &0 &0\\ 0 &0 &0 &0 &0 &0 &0 &20 &-50 &30 &0 &0\\ 0 &0 &0 &0 &0 &0 &0 &0 &15 &-40 &25 &0\\ 0 &0 &0 &0 &0 &0 &0 &0 &0 &80 &-160 &80\\ 0 &0 &0 &0 &0 &0 &25 &0 &0 &0 &25 &-50 \end{array}\right). \end{equation} $

下面将证明该$ Q $矩阵可以由环形部分的任意两相邻状态以及树形部分的叶子状态的击中时和逗留时的概率密度函数所决定.

按照算法6.2, 它们可由状态$ 1, 2, 3, 4 $和$ 8 $到$ 12 $之间任何两个状态的观测确定.根据等价性, 可观测$ 1, 2, $$ 3, 4, 9, 10 $来确定.按照注6.2之技巧, 现通过更少的状态$ 1, 2, 3, 9, 10 $来确定.

本文把计算分为两步:拟合出必要的击中时和逗留时的概率密度函数, 这里省去.并由此计算得到相应的$ \pi_i, q_i, c^{(i)}_n (i = 1, 2, 3, 9, 10) $和$ c^{(9, 10)}_n $.

第二步  计算出转移速率.

首先, 由$ f_{\sigma^{(i)}}(t) $和$ q_i = \frac{1}{E\sigma} $得

(7.2) $ \begin{equation} \begin{array}{lll} &q_1 = q_{15} = 10, \qquad &\pi_1 = 0.00933126, \\ &q_2 = q_{25} = 25. &\pi_2 = 0.01119751, \\ &q_3 = q_{36} = 30, \qquad&\pi_3 = 0.02488336, \\ &q_9 = q_{98}+q_{9, 10} = 50, &\pi_9 = 0.11197512, \\ &q_{10} = q_{10, 9}+q_{10, 11} = 40, &\pi_{10} = =0.22395023. \end{array} \end{equation} $

而且, 可计算出关于状态$ 1 $的$ c^{(1)}_n $.

$ c^{(1)}_1 = 0.09331260, \qquad c^{(1)}_2 = 0.46656299, {\qquad} c^{(1)}_3 = 23.32814930, $

$ c^{(1)}_4 = 1411.35303266, {\qquad} c^{(1)}_5 = 92437.79160185. $

同理可得其它状态的.

$ \begin{array}{llll} &c^{(2)}_1 = 0.27993779, \qquad &c^{(3)}_1 = 0.74650078, \\ &c^{(2)}_2 = 4.19906687, \qquad &c^{(3)}_2 = 7.46500778, \\ &c^{(2)}_3 = 209.95334370, \qquad &c^{(3)}_3 = 298.60031104, \\ &c^{(2)}_4 = 11337.48055988, \quad &c^{(3)}_4 = 14743.39035770, \\ &c^{(2)}_5 = 658203.73250389; \quad &c^{(3)}_5 = 810886.46967340;\\ &c^{(9)}_1 = 5.59875583, \qquad &c^{(10)}_1 = 8.95800933, \\ &c^{(9)}_2 = 162.36391913, \qquad &c^{(10)}_2 = 548.67807154, \\ &c^{(9)}_3 = 10413.68584759, \qquad &c^{(10)}_3 = 76702.95489891, \\ &c^{(9)}_4 = 839253.49922239, \quad &c^{(10)}_4 = 12714774.49455674, \\ &c^{(9)}_5 = 80949611.19751182; \quad &c^{(10)}_5 = 2196279937.79159550;\\ &c^{(9, 10)}_1 = 7.83825816, \qquad &c^{(9, 10)}_2 = 184.75894246. \end{array} $

因此, 由算法6.2, 可得

$ q_{51} = \frac{c^{(1)}_2}{c^{(1)}_1} = 4.99999989, {\qquad} q_{52} = \frac{c^{(2)}_2}{c^{(2)}_1} = 15.00000007, $

$ q_{63} = \frac{c^{(3)}_2}{c^{(3)}_1} = 9.99999997, {\qquad} q_{6} = \frac{c^{(3)}_3}{c^{(3)}_2} = 39.99999998, $

$ q_{5} = \frac{c^{(1)}_3}{c^{(1)}_2} = 50.00000005, {\qquad} q_{57} = q_5-q_{51}-q_{52} = 30.00000009 , $

$ \pi_5 = \frac{[c^{(1)}_1]^2}{c^{(1)}_2} = 0.01866252, {\qquad} \pi_6 = \frac{[c^{(3)}_1]^2}{c^{(3)}_2} = 0.07465008, $

$ q_{75} = \frac{\frac{c^{(1)}_4}{c^{(1)}_2}-q_{52}q_{25}-q_5^{2}}{q_{57}} = 4.99999876, {\qquad} \pi_7 = \frac{\pi_5q_{57}}{q_{75}} = 0.11197514, $

于是有

$ q_{7} = \frac{\frac{c^{(1)}_5}{c^{(1)}_2}-q_{52}q_2q_{25}-q^{3}_5-2q_5(q_{52}q_{25}+q_{57}q_{75})}{q_{57}q_{75}} = 75.00002725. $

接下来, 由$ c^{(9, 10)}_1, c^{(9, 10)}_2 $, 可得$ q_{98} = 20.00000000, q_{10, 11} = 25.00000000 $, 于是可得

$ q_{9, 10} = q_9-q_{98} = 30.00000000, \quad q_{10, 9} = q_{10}-q_{10, 11} = 15.00000000. $

相似地, 由$ c^{(9)}_1 $和$ c^{(9)}_2 $, 可得

$ \pi_{8} = 0.04479005 , \qquad q_{8, 9} = 50.00000000, $

再由$ c^{(9)}_3 $, 可得

$ q_{8} = \frac{c^{(9)}_3-\pi_{10}q^2_{10, 9}q_{10}}{\pi_{8}q^2_{89}} = 74.99999454, $

$ q_{87} = q_8-q_{89} = 24.99999454, {\qquad} q_{78} = \frac{\pi_8q_{87}}{\pi_7} = 9.99999684. $

最后, 由$ c^{(10)}_1 $和$ c^{(10)}_2 $, 可得

$ \pi_{11} = 0.06998445 , \qquad q_{11, 10} = 80.00000000, $

再由$ c^{(10)}_3, c^{(10)}_4, c^{(10)}_5 $获得

$ q_{11} = \frac{c^{(10)}_3-\pi_{9}q^2_{9, 10}q_{9}}{\pi_{11}q^2_{11, 10}} = 159.99999486, \qquad q_{11, 12} = q_{11}-q_{11, 10} = 79.99999486, $

$ q_{12, 11} = \frac{c^{(10)}_4-\pi_9q^{2}_{9, 10}(q^{2}_9+q_{98}q_{89})-\pi_{11}q^{2}_{11, 10}q^{2}_{11}}{\pi_{11}q^{2}_{11, 10}q_{11, 12}} = 25.00002217, \\ $

$ \begin{eqnarray*} q_{12}& = &\frac{c^{(10)}_5-\pi_9q^{2}_{9, 10}(q^{3}_9+2q_9q_{98}q_{89}+q_{98}q_8q_{89})-\pi_{11}q^{2}_{11, 10}(q^{3}_{11}+2q_{11}q_{11, 12}q_{12, 11})}{\pi_{11}q^{2}_{11, 10}q_{11, 12}q_{12, 11}} \\ & = &50.00018770, \end{eqnarray*} $

$ \pi_{12} = \frac{\pi_{11}q_{11, 12}}{q_{12, 11}} = 0.22395002, \qquad q_{12, 7} = q_{12}-q_{12, 11} = 25.00016553, $

$ q_{7, 12} = \frac{\pi_{12}q_{12, 7}}{\pi_7} = 50.00027301, \qquad q_{76} = q_7-q_{75}-q_{78}-q_{7, 12} = 9.99976980, $

$ \pi_{67} = \frac{\pi_7q_{76}}{\pi_6} = 14.99951271, \qquad q_{64} = q_{6}-q_{63}-q_{67} = 15.0004873, $

$ \pi_4 = 1-\sum\limits_{i\neq 4} = 0.07465008, \qquad q_{46} = \frac{\pi_6q_{64}}{\pi_4} = 15.00063198. $

故, 由上可得$ q_4 = q_{46} = 15.00063198. $

至此, 所有转移速率都求出来了.

不难发现该方法是正确的, 而且是非常有效的.

本文完成了有环的可逆马尔可夫链的统计确认问题, 这也是最重要和最关键的一类马尔可夫链.结论是:有环的可逆马尔可夫链是可通过马尔可夫链反演法来确定的.随着本文的有环链和之前的无环链的确定, 可逆马尔可夫链的统计确认已经形成了系统的理论和成熟的算法.为了进一步完善该理论并拓展应用范围, 未来将探索有着更广泛应用的不可逆马尔可夫链的统计确认问题, 尽管这可能非常困难.