1 引言
分辨率的概念在众多领域中有重要作用.显示分辨率是指显示器能够显示的像素数;图像分辨率指单位长度的图像中包含的像素点数;角分辨率是指两个相邻的目标信号能被雷达分辨时的最小相隔角度;时间分辨率是将连续变化过程离散化后的最小时间间隔;空间分辨率是遥感图像中能够辨别临界距离的最小极限.此外,分辨率在工程技术等领域应用广泛,如在光学中,像分辨本领被用来判断两个相邻物点的像能否被分开[1];在谱估计中,谱估计分辨率是指利用白噪声中的双正弦分辨特性评价不同谱估计方法中的分辨率[2];在雷达监测中,雷达角分辨率被用来表示雷达的指向精度,雷达波长越长,雷达角分辨率越低[3];在描述人的听觉时,分辨率被用来描述人耳能够辨识并区分声音的频率宽度[4].分辨率在其它学科领域也有广泛应用,数字信号处理中的频率分辨率是指算法将两个相近的信号谱峰分开的能力,不仅与信号处理的算法有关,而且受信号中信噪比等因素的影响[5].
上述分辨率的概念都是对特定参数而言. 2019年,鲁纳纳等[6]研究过参数分辨率的相关问题,本文在其基础上,给出了参数分辨率的完整概念和计算方法,并将参数分辨率应用于实例中.参数分辨率是指从区分一般参数的角度,给出相近信号能否被区分的一个标准,用于评价算法对相近参数(信号)的区分能力.最小二乘法与全最小一乘法是一元线性回归模型常用的参数估计方法,其理论研究完善[7],并且应用广泛[8],因此采用最小二乘法与全最小一乘法对一元线性回归模型进行参数分辨率分析,并给出参数分辨率的具体定义和计算方法.实验结果表明两种算法均具有性质:随信噪比的增大,参数分辨率的精度增高,即两个相近信号越容易被分开;对线性回归模型而言,局部参数分辨率与整体参数分辨率保持一致;线性噪声信号中噪声标准差与最小二乘参数分辨率满足线性关系,并利用区间估计理论给出了证明,该线性关系的发现为计算线性回归模型的参数分辨率提供了一种预测方式.最后,对两段相似的音频信号,分别采用最小二乘法和全最小一乘法进行参数分辨率分析,实验结果进一步说明了参数分辨率的合理性和有效性.
2 参数分辨率的引入
现有分辨率的概念均是从区分特定参数的角度出发,给出算法对相近信号(参数)的区分能力,这些概念都比较有针对性,而本文提出的是一种更加宽泛的分辨率概念:参数分辨率.参数分辨率概念的核心是从区分一般参数的角度出发,给出相近信号可以被分开的标准,用于衡量算法对相近信号的区分能力.该区分标准可以是相近信号被分开的最小间隔,也可以是相近信号不能被分开的最大间隔,本文选用前者作为区分标准.
参数分辨率的基本思想是对给定的两段相近信号,利用参数估计算法对信号中的参数进行估计,通过判断两组估计参数能否被分开,进而判断这两段相近信号能否被分开.但是判断参数能否被分开是一个比较困难的问题,因为缺乏对参数的标签,所以引入无监督学习中的聚类算法.为了给出两组参数可以被区分的标准,设置聚类准确率
定义2.1 (参数分辨率的一般定义) 在
准确率
参数分辨率的产生与模型参数、信噪比以及信号噪声等因素有关,因此下面将通过计算最小二乘法和全最小一乘法对一元线性回归模型的参数分辨率,说明参数分辨率的合理性、可行性和有效性.
3 准备工作
3.1 最小二乘法的相关原理
最小二乘法(LS)是提供“观测组合”的主要工具之一,它依据对某事件的大量观测而获得“最佳”成果和“最可能”表现形式.
对于一元线性回归模型
最小二乘法的目标为估计得到的参数
其中
由于
这就是参数
(1)它们是独立正态变量
所以,在线性回归模型下有
(2)它们满足Gauss-Markov定理:在线性回归模型中,如果误差满足零均值、同方差且互不相关,则回归系数的最佳线性无偏估计就是最小二乘估计.
3.2 全最小一乘法的相关原理
设样本点为
回归直线为
设过直线的两个样本点为
于是直线方程为
所有样本点
那么与
3.3 实验步骤
本小结以一元线性回归模型和最小二乘法为例,给出参数分辨率的计算方法和最小二乘参数分辨率的具体定义.
Step1 产生含参的噪声信号和参数的估计值
(1)产生原始信号
对于线性回归模型
(2)计算噪声强度(NP)
固定信噪比SNR,利用公式
(3)产生噪声信号
首先产生一组服从标准正态分布的随机数
(4)检验随机数的稳健性
利用由随机数
比较其和原先给定的信噪比
(5)产生参数的估计值
对两个噪声信号
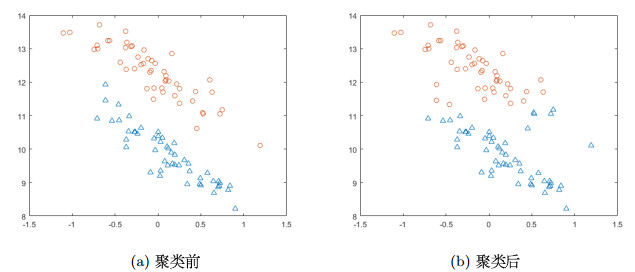
图 1
Step2 引入聚类算法,给出两个相近信号可以被区分的标准
由表 1可知,密度峰值聚类相较k-means聚类和模糊聚类对点的类判别较准确,即误判点的个数少于其他的聚类算法.此外,还可以使用Fisher判别准则或其它分类较准确的聚类方法.
密度峰值聚类的核心思想是对聚类中心的刻画,聚类中心应同时具有两个特点: (ⅰ)本身的密度大,即它被密度均不超过它的邻居包围; (ⅱ)与其他密度更大的数据点之间“距离”相对更大.密度峰值聚类的聚类步骤
(ⅰ)计算每个点的局部密度
(ⅱ)计算一个将
(ⅲ)计算其余的点到这两个聚类中心的距离,距离较小的归为一类.
设聚类的点的总个数为
定义3.1 (最小二乘参数分辨率的定义) 在
4 实验结果与分析
对于一元线性回归模型
4.1 基于相对误差的LS参数分辨率与参数变化的影响分析
固定参数
表 2 不同聚类算法的判别结果
| SNR | 分开值1 | RE1 (%) | 分开值2 | RE2 (%) | |RE1 - RE2| (%) |
| 30 | 10.198 | 1.98 | 9.807 | 1.93 | 0.06 |
| 40 | 10.064 | 0.64 | 9.937 | 0.63 | 0.01 |
| 50 | 10.020 | 0.20 | 9.980 | 0.20 | 0 |
| 60 | 10.007 | 0.07 | 9.993 | 0.07 | 0 |
| 70 | 10.002 | 0.02 | 9.998 | 0.02 | 0 |
| 80 | 10.001 | 0.01 | 9.999 | 0.01 | 0 |
由表 2的最后一列知,参数
4.2 基于相对误差的LS参数分辨率与信噪比的影响分析
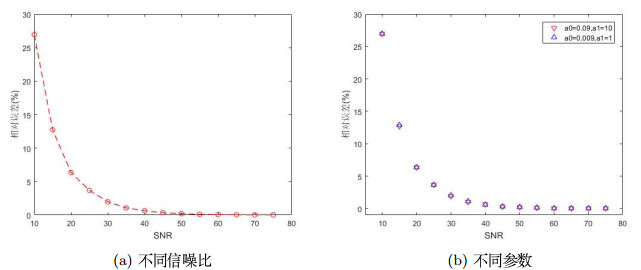
图 2
参数分辨率是指参数估计中,两个相近信号能被分开的最小间隔.最小间隔越小,参数分辨率的精度越高. 图 2(a)中点线表示可以区分两个相近信号时参数间的最短距离,即参数分辨率.线以下表示参数间的距离小于参数分辨率,算法不能有效地区分这两组数据,即两个相近的信号不能被区分开,此时只能把两个信号看成同一个信号.线以上表示参数间的距离大于参数分辨率,算法能够有效区分这两组数据,此时参数对信号的影响差别不能忽略,尤其是在信号分离中,需看成两个不同的信号.由图 2(a)可知,随着信噪比的增大,相对误差减小,参数分辨率的精度提高,即两个相近信号越容易被分开,这与实际情况相吻合,说明本文提出的参数分辨率概念是合理的.
参数
4.3 基于绝对误差的LS参数分辨率与噪声方差的影响分析
本小节主要研究噪声方差和基于绝对误差的参数分辨率之间的关系.因两个一元线性回归模型
图 3
这预示线性噪声中噪声的标准差与基于绝对误差的参数分辨率满足线性关系.
定理4.1 一元线性噪声信号中噪声的标准差
其中
证 对噪声信号
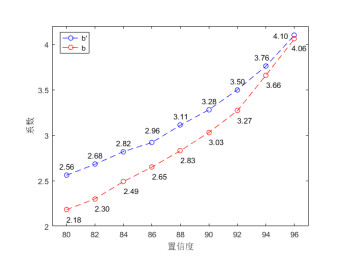
图 4
选取枢轴量
经不等式变形可得
由于标准正态分布为单峰对称的,所以在
由
由于置信区间长度与参数分辨率是同一事件的两种表现形式,即准确率为
注4.1 参数分辨率的准确率和置信区间的置信度是一一对应的,固定参数分辨率的成功率
图 5
4.4 不同算法对同一模型的参数分辨率分析
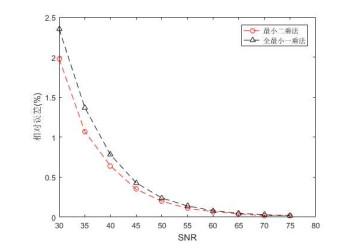
参数分辨率是衡量算法准确度的有效指标.基于绝对误差与相对误差,通过实验分析全最小一乘参数分辨率与信噪比、方差等因素的关系,可以得到与最小二乘法相似的结果.此节只列出基于相对误差的不同信噪比下的最小二乘法与全最小一乘法参数分辨率结果.
由图 6可知,在高斯噪声下,最小二乘参数分辨率在所有的信噪比范围内都优于全最小一乘参数分辨率,所以相较全最小一乘法,最小二乘法对一元线性回归模型的参数估计准确度更高,这与Gauss-Markov定理是一致的,说明参数分辨率作为信号划分的评判标准是有效的.
图 6
5 实例分析
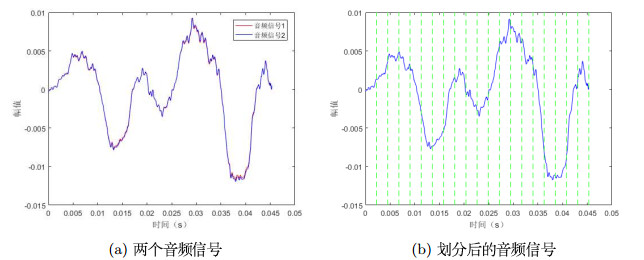
不同算法对同一组信号的区分能力是有差异的.截取一段低音提琴的音频信号
图 7
(1)将音频信号分成
(2)将每一段中的
(3)使用相同的模型和不同的算法拟合(2)中的
(4)计算每一段信号拟合后的决定系数
通过对每一段信号的线性拟合,原始信号就变成了逐段线性的信号,并且每一段原始信号由对应线性信号的斜率参数与截距参数决定.为了判断两段相近信号能否被分开,设置参数
本例中,令
6 总结
参数分辨率是对分辨率概念的自然延伸,是衡量两个相近信号能否分开的一个标准,是评价模型及算法准确度的有效指标.本文结合聚类的思想,给出参数分辨率的定义和计算方法,分别用最小二乘法与全最小一乘法对一元线性回归模型进行参数分辨率分析,从而说明参数分辨率概念的合理性、可行性和有效性.实验结果表明两种算法均具有性质:随着信噪比的增大,参数分辨率的精度增高,即相近信号越容易被分开;对线性回归模型而言,局部参数分辨率与整体参数分辨率保持一致.此外,利用区间估计理论证明了线性噪声信号中噪声标准差与最小二乘参数分辨率满足线性关系,这为计算线性回归模型的参数分辨率提供了一种预测方式.最后,对两段相似的音频信号,分别采用最小二乘法和全最小一乘法进行参数分辨率分析,实验结果进一步说明了参数分辨率的合理性和有效性.参数分辨率的提出,不仅为区分相近信号提供了新的解决方法,而且为评估模型及算法的准确度提供了新的参考依据.待研究的问题有高维最小二乘法的参数分辨率,其它模型及算法的参数分辨率等.
参考文献
低采样率高分辨率压缩功率谱估计方法的仿真研究
Simulation on low sampling rate high resolution compressed power spectrum estimation method
基于MUSIC算法高频地波雷达的角分辨率
Angle resolution of HK ground wave radar based on MUSIC scheme
Piecewise-linear frequency shifting algorithm for frequency resolution enhancement in digital hearing aids
Fine resolution frequency estimation from three DFT samples:case of windowed data
DOI:10.1016/j.sigpro.2015.03.009 [本文引用: 1]
EM算法的参数分辨率
Research on resolution based on EM algorithm
Online detection of broken rotor bar fault in induction motors by combining estimation of signal parameters via min-norm algorithm and square method
DOI:10.1007/s10033-017-0185-2 [本文引用: 1]
关于加权全最小一乘法
On weighted total least absolute deviations
K-means聚类算法研究综述
Review of k-means clustering algorithm
模糊聚类理论发展及应用的研究进展
Research progress in the development and application of fuzzy clustering theory
Cluster by fast search and find of density peaks
DOI:10.1126/science.1242072 [本文引用: 1]