1 引言
在对流体的数值模拟中,有两种典型的数值方法:拉格朗日方法和欧拉方法.欧拉法能够处理大变形问题,但是由于输运计算会带来误差,同时很难给出精确的材料界面.拉格朗日方法的网格完全跟随流体运动,能够用网格边界清晰地捕捉材料界面;但是当涉及大变形时,网格会产生扭曲,需要结合网格重分和物理量重映来保证模拟的正常实施.
考虑到拉格朗日方法能很好地计算流体界面,在可压缩流体流动的数值模拟中能够很好地处理间断问题,同时非结构三角形网格在处理复杂几何问题时具有明显的优势,本文给出一种使用RKDG方法在非结构网格上求解的拉格朗日格式.本文格式是一种半拉格朗日格式,格式中变量的梯度算子和散度算子采用欧拉坐标表示,时间导数采用拉格朗日坐标表示,从而省去了求解映射雅可比矩阵的步骤,简化了计算过程.在本文格式中,网格节点跟随流体运动,节点速度的求解方法是文献[4]中四边形网格节点速度求解方法向三角形网格的延伸,算法依据文献[5]中的相关内容进行改进,格式选取顶点沿边的熵波速度来代替文献[4]算法中的边法向速度的Roe平均.为了保证模拟的稳定实施,本文利用非结构三角形网格上的HWENO(Hermite weighted essential non-oscillatory)重构来控制间断附近产生的虚假振荡.一些数值算例验证了格式在非结构网格上的二阶精度和鲁棒性.
本文的基本内容如下:第2节给出了欧拉方程组的拉格朗日形式.第3节给出非结构三角形网格上使用RKDG方法求解拉氏(拉格朗日)方程组弱形式的基本过程.第4节给出的算例验证了算法的性能.
2 拉式框架下可压缩欧拉方程组的弱形式
在本节,参照文献[6]的做法,我们首先给出了可压缩欧拉方程组的拉格朗日形式,同时给出用于求解的积分弱形式.欧拉框架下的无源可压缩流体力学方程组为
其中,未知量为流体密度
设可压缩流体在初始时刻的区域为
其中
由于映射可逆,且
其中
设一个依赖欧拉坐标的流场物理量:
结合轨迹方程,可得
其中
将守恒变量
对于任意的测试函数
在空间
由于映射
已知在某一时刻
3 RKDG方法
3.1 空间离散
本节将采用间断有限元(DG)方法对弱形式(2.10)进行空间离散化.
首先,对计算空间进行网格划分.初始时刻计算区域为
其中
定义
其中
使用间断有限元求解(2.10)式的过程如下:寻求一个数值解
对所有的检验函数
其中
由格林公式,可得
其中
由于(3.2)式对所有的检验函数成立,检验函数选取为基函数
其中
(3.3)式演化为
其中
3.2 时间离散与斜率限制器
本节首先给出网格节点移动速度的选取方式.我们对[4]中的四边形网格速度求解器进行延伸,获得适用于非结构网格的拉格朗日速度.在非结构网格上,假设连接一个顶点
顶点
步骤1 设
其中,
步骤3 设
结合所有线段在
对于分片多项式逼近, DG方法将导致在强间断处产生虚假振荡.本文采用一种非结构三角形网格上的HWENO重构(参见文献[3])作为限制器控制虚假振荡.该重构保持了DG方法的紧致性,完美地达到了压制虚假振荡的效果.
4 数值算例
4.1 精度测试
我们考虑二维低密度流问题,检测本文格式的精度.初始条件为:
表 1 格式关于密度的误差和精度
| order | order | order | ||||
| 7.07E-002 | 2.1029E-002 | 2.4996E-002 | 6.8346E-002 | |||
| 3.51E-002 | 5.5261E-003 | 1.9280 | 6.7907E-003 | 1.8800 | 1.7204E-002 | 1.9900 |
| 1.76E-002 | 1.4303E-003 | 1.9498 | 1.8440E-003 | 1.8806 | 4.6818E-003 | 1.8776 |
| 8.31E-003 | 3.6687E-004 | 1.9630 | 5.0124E-004 | 1.8793 | 1.4688E-003 | 1.8724 |
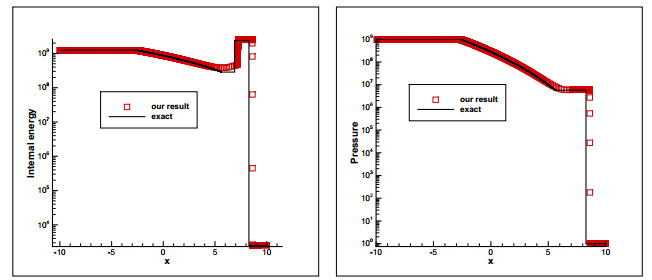
4.2 Leblanc激波管问题
该激波管问题的初始条件为:
图 1
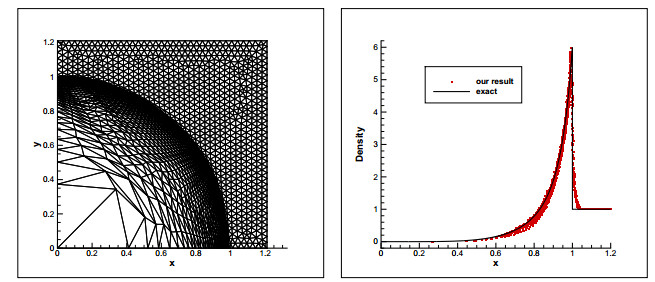
4.3 Sedov问题
Sedov问题是一个包含由强爆破产生的圆柱对称型强激波传播过程的经典算例,它经常被用于测试拉式格式的鲁棒性.该问题的计算区域设为
图 2
从图中可以看出格式得到的结果很好地逼近了精确解,同时很好地保持了网格的良好品质和解的对称性.
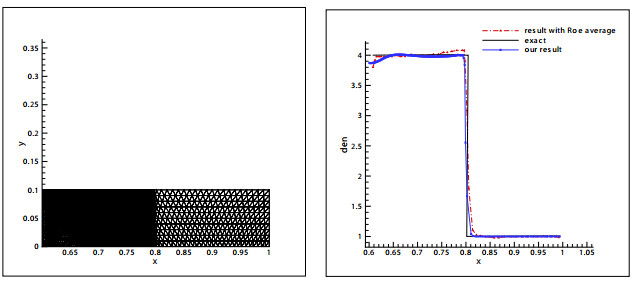
4.4 Salzman问题
Salzman问题被广泛应用于拉式算法的健壮性测试中.本算例的初始计算区域为
图 3
参考文献
The Runge-Kutta discontinuous Galerkin method for conservation laws Ⅱ:general framework
On the computation of multi-material flows using ALE formulation
DOI:10.1016/j.jcp.2003.09.026 [本文引用: 1]
A hermite WENO-based limiter for discontinuous Galerkin method on unstructured grids
A high order ENO conservative Lagrangian type scheme for the compressible Euler equations
DOI:10.1016/j.jcp.2007.09.017 [本文引用: 6]
Positivity-preserving Lagrangian scheme for multi-material compressible flow
DOI:10.1016/j.jcp.2013.09.047 [本文引用: 2]
A Cell-Centered Lagrangian scheme for two-dimensional compressible flow problems
DOI:10.1137/050633019 [本文引用: 1]
High order Lagrangian ADER-WENO schemes on unstructured meshes-application of several node solvers to hydrodynamics and magnetohydrodynamics
DOI:10.1002/fld.3947 [本文引用: 1]
An arbitrary Lagrangian-Eulerian RKDG method for compressible Euler equations on unstructured meshes:Single-material flow
DOI:10.1016/j.jcp.2019.07.015 [本文引用: 1]