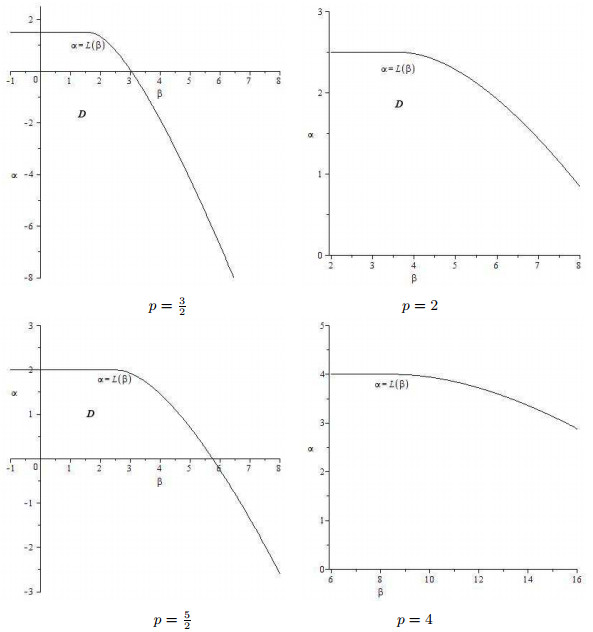
图 1
参数 p = \frac{3}{2}, 2, \frac{5}{2}, 4 D \alpha = L(\beta)
由引理2.6和(2.9)式知:当且仅当 \beta\leq \inf\limits_{r\in(0, 1)}[1+h(r)] = (p^2+1)/2 {G_{\beta}}'(r)>0 r\in(0, 1) G_{\beta}(r) (0, 1) \beta>(p^2+1)/2 \lambda = \lambda(\beta)\in(0, 1) r\in(0, \lambda) G_{\beta}'(r)<0 r\in(\lambda, 1) G_{\beta}'(r)>0 G_{\beta}(r) (0, 1) L(\beta)<p G_{\beta}(r) (0, 1) (L(\beta), \infty) .
子情形1.2 \beta\leq (p^2+1)/2 \alpha>p . 则由(3.1)和(3.2)式,引理2.8(1)及其类似子情形1.1的讨论可知:当 \alpha>p \beta\leq (p^2+1)/2 x_{0}, y_{0}\in(0, r_{1}) x_{1}, y_{1}\in(r_{1}, 1) E_{p}\left(H_{\alpha}(x_{0}, y_{0})\right)\leq H_{\beta}\left({E_{p}}(x_{0}), {E_{p}}(y_{0})\right) E_{p}\left(H_{\alpha}(x_{1}, y_{1})\right)\geq H_{\beta}\left({E_{p}}(x_{1}), {E_{p}}(y_{1})\right) . 因此, E_{p} (0, 1) H_{\alpha, \beta} H_{\alpha, \beta}
[1]
Abramowitz M , Stegun I A . Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Washington : US Government Printing Office , 1964
[本文引用: 1]
[2]
Lehto O , Virtanen K I . Quasiconformal Mappings in the Plane. New York : Springer-Verlag , 1973
[本文引用: 1]
[3]
Anderson G D , Vamanamurthy M K , Vuorinen M . Conformal Invariants, Inequalities, and Quasiconformal Maps. New York : John Wiley & Sons , 1997
[本文引用: 2]
[5]
Wang M K , Chu Y M , Qiu Y F , Qiu S L . An optimal power mean inequality for the complete elliptic integrals
Appl Math Lett, 2011 , 24 6 ): 887 - 890
DOI:10.1016/j.aml.2010.12.044
[6]
Wang G D , Zhang X H , Chu Y M . A power mean inequality for the Grötzsch ring function
Math Inequal Appl, 2011 , 14 4 ): 833 - 837
URL
[7]
Chu Y M , Wang M K , Qiu S L . Optimal combinations bounds of root-square and arithmetic means for Toader mean
Proc Indian Acad Sci Math Sci, 2012 , 122 1 ): 41 - 51
DOI:10.1007/s12044-012-0062-y
[8]
Wang M K , Chu Y M , Qiu S L , Jiang Y P . Bounds for the perimeter of an ellipse
J Approx Theory, 2012 , 164 7 ): 928 - 937
DOI:10.1016/j.jat.2012.03.011
[9]
Chu Y M , Qiu Y F , Wang M K . Hölder mean inequalities for the complete elliptic integrals
Integral Transforms Spec Funct, 2012 , 23 7 ): 521 - 527
DOI:10.1080/10652469.2011.609482
[10]
Wang G D , Zhang X H , Chu Y M . A power mean inequality involving the complete elliptic integrals
Rocky Mountain J Math, 2014 , 44 5 ): 1661 - 1667
DOI:10.1216/RMJ-2014-44-5-1661
[11]
Yang Z H, Qian W M, Chu Y M, Zhang W. Monotonicity rule for the quotient of two functions and its application. J Inequal Appl, 2017, Article: 106
[12]
Qian W M, Chu Y M. Sharp bounds for a special quasi-arithmetic mean in terms of arithmetic and geometric means with two parameters. J Inequal Appl, 2017, Article: 274
[13]
Yang Z H , Qian W M , Chu Y M , Zhang W . On approximating the arithmetic-geometric mean and complete elliptic integral of the first kind
J Math Anal Appl, 2018 , 462 2 ): 1714 - 1726
URL
[14]
Huang T R, Tan S Y, Ma X Y, Chu Y M. Monotonicity properties and bounds for the complete p -elliptic integrals. J Inequal Appl, 2018, Article: 239
[15]
Zhao T H, Wang M K, Zhang W, Chu Y M. Quadratic transformation inequalities for Gaussian hypergeometric function. J Inequal Appl, 2018, Article: 251
[16]
Yang Z H , Qian W M , Chu Y M . Monotonicity properties and bounds involving the complete elliptic integrals of the first kind
Math Inequal Appl, 2018 , 21 4 ): 1185 - 1199
URL
[17]
Yang Z H , Chu Y M , Zhang W . High accuracy asymptotic bounds for the complete elliptic integral of the second kind
Appl Math Comput, 2019 , 348 552 - 564
URL
[18]
Zhao T H, Zhou B C, Wang M K, Chu Y M. On approximating the quasi-arithmetic mean. J Inequal Appl, 2019, Article: 42
[19]
Wang J L, Qian W M, He Z Y, Chu Y M. On approximating the Toader mean by other bivariate means. J Funct Spaces, 2019, Article ID: 6082413
[20]
Wang M K , Chu Y M , Zhang W . Monotonicity and inequalities involving zero-balanced hypergeometric function
Math Inequal Appl, 2019 , 22 2 ): 601 - 617
URL
[21]
Qiu S L , Ma X Y , Chu Y M . Sharp Landen transformation inequalities for hypergeometric functions, with applications
J Math Anal Appl, 2019 , 474 2 ): 1306 - 1337
URL
[本文引用: 1]
[23]
Drábek P , Manásevich R . On the closed solution to some nonhomogeneous eigenvalue problems with p -Laplacian
Differential Integral Equations, 1999 , 12 6 ): 773 - 788
URL
[本文引用: 1]
[24]
Kobayashi H , Takeuchi S . Applications of generalized trigonometric functions with two parameters
Commun Pure Appl Anal, 2019 , 18 3 ): 1509 - 1521
DOI:10.3934/cpaa.2019072
[25]
Takeuchi S. Applications of generalized trigonometric functions with two parameters Ⅱ. 2019, arXiv: 1904.01827
[本文引用: 1]
[26]
Takeuchi S . Legendre-type relations for generalized complete elliptic integrals
J Class Anal, 2016 , 9 1 ): 35 - 42
URL
[本文引用: 1]
[28]
Wang M K , Zhang W , Chu Y M . Monotonicity, convexity and inequalities involving the generalized elliptic integrals
Acta Math Sci, 2019 , 39B 5 ): 1440 - 1450
URL
[本文引用: 1]
[29]
Wang M K, Chu H H, Chu Y M. Precise bounds for the weighted Hölder mean of the complete p -elliptic integrals. J Math Anal Appl, 2019, 480 (2), Article ID: 123388
[本文引用: 1]
[30]
Huang T R, Han B W, Ma X Y, Chu Y M. Optimal bounds for the generalized Euler-Mascheroni constant. J Inequal Appl 2018, Article: 118
[本文引用: 1]
[31]
Zaheer Ullah S, Adil Khan M, Chu Y M. A note on generalized convex functions. J Inequal Appl, 2019, Article: 291
[本文引用: 1]
[32]
Zhang X H . Monotonicity and functional inequalities for the complete p -elliptic integrals
J Math Anal Appl, 2017 , 453 2 ): 942 - 953
URL
[本文引用: 2]
[33]
Anderson G D , Qiu S L , Vamanamurthy M K , Vuorinen M . Generalized elliptic integrals and modular equations
Pacific J Math, 2000 , 192 1 ): 1 - 37
DOI:10.2140/pjm.2000.192.1
[本文引用: 1]
[35]
Anderson G D , Sugawa T , Vamanamurthy M K , Vourinen M . Twice-punctured hyperbolic sphere with a conical singularity and generalized elliptic integral
Math Z, 2010 , 266 1 ): 181 - 191
DOI:10.1007/s00209-009-0560-5
[36]
Neuman E . Inequalities and bounds for generalized complete elliptic integrals
J Math Anal Appl, 2011 , 373 1 ): 203 - 213
URL
[37]
Bhayo B A , Vuorinen M . On generalized complete elliptic integrals and modular functions
Proc Edinb Math Soc (2), 2012 , 55 3 ): 591 - 611
DOI:10.1017/S0013091511000356
[38]
Yang Z H , Chu Y M . A monotonicity property involving the generalized elliptic integral of the first kind
Math Inequal Appl, 2017 , 20 3 ): 729 - 735
URL
[39]
Wang M K , Li Y M , Chu Y M . Inequalities and infinite product formula for Ramanujan generalized modular equation function
Ramanujan J, 2018 , 46 1 ): 189 - 200
DOI:10.1007/s11139-017-9888-3
[40]
Wang M K , Chu Y M , Zhang W . The precise estimates for the solution of Ramanujan's generalized modular equation
Ramanujan J, 2019 , 49 3 ): 653 - 668
DOI:10.1007/s11139-018-0130-8
[本文引用: 1]
[41]
He X H , Qian W M , Xu H Z , Chu Y M . Sharp power mean bounds for two Sándor-Yang means
Rev R Acad Cienc Exactas Fís Nat Ser A Mat, 2019 , 113 3 ): 2627 - 2638
DOI:10.1007/s13398-019-00643-2
[42]
Qian W M, Yang Y Y, Zhang H W, Chu Y M. Optimal two-parameter geometric and arithmetic mean bounds for the Sándor-Yang mean. J Inequal Appl, 2019, Article: 287
[43]
Bullen P S . Handbook of Means and Their Inequalities. Dordrecht : Kluwer Academic Publishers Group , 2003
[本文引用: 1]
[45]
Baricz Á. Convexity of the zero-balanced Gaussian hypergeometric functions with respect to Hölder means. JIPAM J Inequal Pure Appl Math, 2007, 8 (2), Article: 40
[本文引用: 1]
[46]
Wang M K , Chu Y M , Qiu S L , Jiang Y P . Convexity of the complete elliptic integrals of the first kind with respect to Hölder means
J Math Anal Appl, 2012 , 388 2 ): 1141 - 1146
DOI:10.1016/j.jmaa.2011.10.063
[本文引用: 1]
[47]
Chu Y M , Wang M K , Jiang Y P , Qiu S L . Concavity of the complete elliptic integrals of the second kind with respect to Hölder means
J Math Anal Appl, 2012 , 395 2 ): 637 - 642
DOI:10.1016/j.jmaa.2012.05.083
[本文引用: 2]
[48]
Zhou L M , Qiu S L , Wang F . Inequalities for the generalized elliptic integrals with respect to Hölder mean
J Math Anal Appl, 2012 , 386 2 ): 641 - 646
DOI:10.1016/j.jmaa.2011.08.026
[本文引用: 1]
[49]
Baricz Á , Bhayo B A , Klén R . Convexity properties of generalized trigonometric and hyperbolic functions
Aequationes Math, 2015 , 89 3 ): 473 - 484
DOI:10.1007/s00010-013-0222-x
[本文引用: 1]
[50]
Baricz Á , Bhayo B A , Vuorinen M . Turán inequalities for generalized inverse trigonometric functions
Filomat, 2015 , 29 2 ): 303 - 313
DOI:10.2298/FIL1502303B
[本文引用: 1]
1
1964
... 令 0<r<1 {\cal K}(r) {\cal E}(r) [1 ] 分别定义为 ...
1
1973
... 在过去的三十多年,完全椭圆积分的研究主要集中于它们在几何函数论中的应用.许多共形不变量、拟共形映射中的偏差函数都可以用完全椭圆积分来表示[2 -3 ] .特别地,关于 {\cal K}(r) {\cal E}(r) [4 -21 ] . ...
2
1997
... 在过去的三十多年,完全椭圆积分的研究主要集中于它们在几何函数论中的应用.许多共形不变量、拟共形映射中的偏差函数都可以用完全椭圆积分来表示[2 -3 ] .特别地,关于 {\cal K}(r) {\cal E}(r) [4 -21 ] . ...
... 引理2.1 [3 ] 对 -\infty<a<b<+\infty f g [a, b] (a, b) (a, b) g'\neq 0 . 如果 f'/g' (a, b)
Bounds for complete elliptic integrals of the first kind
1
2010
... 在过去的三十多年,完全椭圆积分的研究主要集中于它们在几何函数论中的应用.许多共形不变量、拟共形映射中的偏差函数都可以用完全椭圆积分来表示[2 -3 ] .特别地,关于 {\cal K}(r) {\cal E}(r) [4 -21 ] . ...
An optimal power mean inequality for the complete elliptic integrals
0
2011
A power mean inequality for the Gr?tzsch ring function
0
2011
Optimal combinations bounds of root-square and arithmetic means for Toader mean
0
2012
Bounds for the perimeter of an ellipse
0
2012
H?lder mean inequalities for the complete elliptic integrals
0
2012
A power mean inequality involving the complete elliptic integrals
0
2014
On approximating the arithmetic-geometric mean and complete elliptic integral of the first kind
0
2018
Monotonicity properties and bounds involving the complete elliptic integrals of the first kind
0
2018
High accuracy asymptotic bounds for the complete elliptic integral of the second kind
0
2019
Monotonicity and inequalities involving zero-balanced hypergeometric function
0
2019
Sharp Landen transformation inequalities for hypergeometric functions, with applications
1
2019
... 在过去的三十多年,完全椭圆积分的研究主要集中于它们在几何函数论中的应用.许多共形不变量、拟共形映射中的偏差函数都可以用完全椭圆积分来表示[2 -3 ] .特别地,关于 {\cal K}(r) {\cal E}(r) [4 -21 ] . ...
A new form of the generalized complete elliptic integrals
4
2016
... 令 p\in(1, \infty) r\in(0, 1) [22 ] 引入了二类完全 p {K}_{p}(r) {E}_{p}(r)
... 近几年,完全 p [22 , 26 ] 证明完全 p K_{p} E_{p}
... 其中对 r\in(0, 1) r' = \sqrt[p]{1-r^p} . 利用式(1.5), Takeuchi[22 , 27 ] 发现了当 p = 3 p = 4 \pi_{p} p 22 ,命题2.8]) ...
... -椭圆积分与经典的Gauss超几何函数具有如下关系(参见文献[22 ,命题2.8]) ...
On the closed solution to some nonhomogeneous eigenvalue problems with p -Laplacian
1
1999
... 易见 \sin_{2}\theta = \sin\theta \pi_{2} = \pi {K}_{2}(r) = {\cal K}(r) {E}_{2}(r) = {\cal E}(r) . \sin_{p}\theta \pi_{p} 1 p - Laplacian方程的特征值问题[23 -25 ] . ...
Applications of generalized trigonometric functions with two parameters
0
2019
1
... 易见 \sin_{2}\theta = \sin\theta \pi_{2} = \pi {K}_{2}(r) = {\cal K}(r) {E}_{2}(r) = {\cal E}(r) . \sin_{p}\theta \pi_{p} 1 p - Laplacian方程的特征值问题[23 -25 ] . ...
Legendre-type relations for generalized complete elliptic integrals
1
2016
... 近几年,完全 p [22 , 26 ] 证明完全 p K_{p} E_{p}
Complete p -elliptic integrals and a computation formula of \pi_{p} for p =4
1
2018
... 其中对 r\in(0, 1) r' = \sqrt[p]{1-r^p} . 利用式(1.5), Takeuchi[22 , 27 ] 发现了当 p = 3 p = 4 \pi_{p} p 22 ,命题2.8]) ...
Monotonicity, convexity and inequalities involving the generalized elliptic integrals
1
2019
... 是Gauss超几何函数[28 -29 ] , a, b, c c\neq 0, -1, -2, \cdots (a)_{0} = 1 (a\neq 0) (a)_{n} = a(a+1)(a+2)(a+3)\cdots(a+n-1) = \Gamma(n+a)/\Gamma(a) (n = 1, 2, 3\cdots) \Gamma(x) = \int_{0}^{\infty}t^{x-1}e^{-t}{\rm d}t [30 -31 ] . ...
1
... 是Gauss超几何函数[28 -29 ] , a, b, c c\neq 0, -1, -2, \cdots (a)_{0} = 1 (a\neq 0) (a)_{n} = a(a+1)(a+2)(a+3)\cdots(a+n-1) = \Gamma(n+a)/\Gamma(a) (n = 1, 2, 3\cdots) \Gamma(x) = \int_{0}^{\infty}t^{x-1}e^{-t}{\rm d}t [30 -31 ] . ...
1
... 是Gauss超几何函数[28 -29 ] , a, b, c c\neq 0, -1, -2, \cdots (a)_{0} = 1 (a\neq 0) (a)_{n} = a(a+1)(a+2)(a+3)\cdots(a+n-1) = \Gamma(n+a)/\Gamma(a) (n = 1, 2, 3\cdots) \Gamma(x) = \int_{0}^{\infty}t^{x-1}e^{-t}{\rm d}t [30 -31 ] . ...
1
... 是Gauss超几何函数[28 -29 ] , a, b, c c\neq 0, -1, -2, \cdots (a)_{0} = 1 (a\neq 0) (a)_{n} = a(a+1)(a+2)(a+3)\cdots(a+n-1) = \Gamma(n+a)/\Gamma(a) (n = 1, 2, 3\cdots) \Gamma(x) = \int_{0}^{\infty}t^{x-1}e^{-t}{\rm d}t [30 -31 ] . ...
Monotonicity and functional inequalities for the complete p -elliptic integrals
2
2017
... 最近,张孝惠[32 ] 将完全椭圆积分 {\cal K}(r) {\cal E}(r) p K_{p}(r) E_{p}(r) . ...
... 证 (1)–(5)可参见文献[32 ,引理3.4(1), (4)–(7)].下证明(6),利用Gauss超几何函数的级数展开可得 ...
Generalized elliptic integrals and modular equations
1
2000
... 完全椭圆积分的另一种重要的广义形式,称为广义椭圆积分 {{\cal K}}_{a}(r) {{\cal E}}_{a}(r) 33 ]).事实上,对 a\in(0, 1) r\in(0, 1) {{\cal K}}_{a}(r) {{\cal E}}_{a}(r)
Turán inequalities for generalized complete elliptic integrals
1
2007
... 更多 {{\cal K}}_{a}(r) {{\cal E}}_{a}(r) 34 -40 ]. ...
Twice-punctured hyperbolic sphere with a conical singularity and generalized elliptic integral
0
2010
Inequalities and bounds for generalized complete elliptic integrals
0
2011
On generalized complete elliptic integrals and modular functions
0
2012
A monotonicity property involving the generalized elliptic integral of the first kind
0
2017
Inequalities and infinite product formula for Ramanujan generalized modular equation function
0
2018
The precise estimates for the solution of Ramanujan's generalized modular equation
1
2019
... 更多 {{\cal K}}_{a}(r) {{\cal E}}_{a}(r) 34 -40 ]. ...
Sharp power mean bounds for two Sándor-Yang means
0
2019
1
2003
... 特别令 \alpha = -1 0 1 H(x, y) = H_{-1}(x, y) G(x, y) = H_{0}(x, y) A(x, y) = H_{1}(x, y) . 众所周知,对固定的 x, y>0 x\neq y H_{\alpha}(x, y) \alpha {{\Bbb R}} \!\! 43 ]. ...
Generalized convexity and inequalities
1
2007
... 2007年,对 \alpha = 0, -1, 1 \beta = 0, -1, 1 [44 ] 探究了由Maclaurin级数定义的函数的 H_{\alpha, \beta} H_{\alpha, \beta} \!\! H_{\alpha, \beta}
1
... Baricz[45 ] 考察了零平衡超几何函数 F(a, b;a+b;x)(a, b>0) (\alpha, \beta)\in\{(\alpha, \beta)|\alpha\leq 2, \beta\geq 0\} {\cal K}(r) (0, 1) H_{\alpha, \beta} {\cal K}(r) (0, 1) H_{\alpha, \beta} [46 ] 证明.类似地,相同作者在文献[47 ]中得到了关于第二类完全椭圆积分在 (0, 1)
Convexity of the complete elliptic integrals of the first kind with respect to H?lder means
1
2012
... Baricz[45 ] 考察了零平衡超几何函数 F(a, b;a+b;x)(a, b>0) (\alpha, \beta)\in\{(\alpha, \beta)|\alpha\leq 2, \beta\geq 0\} {\cal K}(r) (0, 1) H_{\alpha, \beta} {\cal K}(r) (0, 1) H_{\alpha, \beta} [46 ] 证明.类似地,相同作者在文献[47 ]中得到了关于第二类完全椭圆积分在 (0, 1)
Concavity of the complete elliptic integrals of the second kind with respect to H?lder means
2
2012
... Baricz[45 ] 考察了零平衡超几何函数 F(a, b;a+b;x)(a, b>0) (\alpha, \beta)\in\{(\alpha, \beta)|\alpha\leq 2, \beta\geq 0\} {\cal K}(r) (0, 1) H_{\alpha, \beta} {\cal K}(r) (0, 1) H_{\alpha, \beta} [46 ] 证明.类似地,相同作者在文献[47 ]中得到了关于第二类完全椭圆积分在 (0, 1)
... 定理1.1 [47 ] 第二类完全椭圆积分 {\cal E}(r) (0, 1) H_{\alpha, \beta}
Inequalities for the generalized elliptic integrals with respect to H?lder mean
1
2012
... 2012年,周丽明等[48 ] 考虑了两类广义椭圆积分,给出了 {\cal K}_{a}(r) (0, 1) H_{\alpha, \alpha} {\cal E}_{a}(r) a\in(0, 1/2] ) 在 (0, 1) H_{\alpha, \alpha} 49 -50 ]中也研究广义三角函数的 H_{\alpha, \alpha}
Convexity properties of generalized trigonometric and hyperbolic functions
1
2015
... 2012年,周丽明等[48 ] 考虑了两类广义椭圆积分,给出了 {\cal K}_{a}(r) (0, 1) H_{\alpha, \alpha} {\cal E}_{a}(r) a\in(0, 1/2] ) 在 (0, 1) H_{\alpha, \alpha} 49 -50 ]中也研究广义三角函数的 H_{\alpha, \alpha}
Turán inequalities for generalized inverse trigonometric functions
1
2015
... 2012年,周丽明等[48 ] 考虑了两类广义椭圆积分,给出了 {\cal K}_{a}(r) (0, 1) H_{\alpha, \alpha} {\cal E}_{a}(r) a\in(0, 1/2] ) 在 (0, 1) H_{\alpha, \alpha} 49 -50 ]中也研究广义三角函数的 H_{\alpha, \alpha}