众所周知,大多数反问题的计算是基于相应正问题的计算.由于反问题的病态性,特别是数值计算的不稳定性,正问题的高精度计算显得尤为重要.有限差分法是数值求解偏微分方程的经典方法.与其他类型的数值方法如有限元法相比较,有限差分法无法适应复杂的区域.但是,有限差分法也有其优点,例如计算格式构造简单,并且容易计算机编程.

本文中,我们考虑以下反初值问题

(1.1) $ \begin{equation} \left\{\begin{array}{ll} u_t-(a(x)u_x)_x = f(x, t), \quad & (x, t)\in Q = [0, l]\times(0, T], \\ u|_{t = 0} = g(x), & x\in [0, l], \end{array}\right. \end{equation} $

其中$ a(x) $是一个给定光滑函数且满足

(1.2) $ \begin{equation} a(0) = a(l) = 0, \; \; \; \; a(x)>0, \; \; x\in(0, l), \end{equation} $

$ f(x, t) $是给定源项,而$ g(x) $是方程(1.1)中的未知函数.假设给定如下附加条件

(1.3) $ \begin{equation} u(x, T) = k(x), \quad x\in[0, l], \end{equation} $

这里$ k(x) $是一个给定观测函数.本文主要研究如何由(1.1)和(1.3)式同时确定$ u $和$ g $.

数学模型(1.1)属于退化抛物型方程^{[1-2, 4, 13]}.根据著名的Fichera退化抛物方程理论(参见文献[10]),我们知道在退化边界上是否应给出边界条件是由Fichera函数的符号所决定的.通过简单的计算,可以很容易地检查在退化边界$ x = 0 $和$ x = l $处,对应的Fichera函数值为零,故而不应给出边界条件.因此,数学模型(1.1)的提法是合适的.

关于非退化抛物方程的反源或初值问题,许多文献均有涉及,如文献[3, 6-8, 14-15]等.但是,比起非退化方程的研究,退化方程反问题的研究却非常少.在文献[10]中,作者研究了重构下列退化抛物型方程

$ u_t-\left(a(x)u_x\right)_x+c(x)u = f(x) $

源项$ f(x) $的反问题.基于最优控制理论,证明了控制泛函极小元的存在性和唯一性,并获得了反问题的数值解.文献[11]讨论了类似的问题,并用极值原理证明了原问题解的唯一性.文献[16]考虑了下列退化抛物型方程

$ u_t-\left(a(x)u_x\right)_x = 0 $

的初值反演问题,利用对数凸性方法证明了解的条件稳定性,并通过Landweber迭代得到了稳定的数值解.

据作者所知,文献[16]应该是第一个研究退化抛物型方程反初值问题的文献.文献[16]中存在两个缺陷

$ \bullet $ 正问题的差分格式只有一阶精度；

$ \bullet $ 反问题的解是由Landweber迭代得到的,其收敛速度很慢.

为了加速收敛,本文采用共轭梯度法来求解数值解.然而,对于二阶退化抛物型方程来说,要提高计算精度似乎并不容易.

Crank-Nicolson方法(CN)是一种广泛应用于抛物型方程的数值方法,其精度为二阶.将CN方法应用于初边值问题,例如,以下非退化模型

(1.4) $ \begin{equation} \left\{\begin{array}{ll} v_t-(\tilde{a}(x)v_x)_x = \tilde{f}(x, t), \quad & (x, t)\in [0, l]\times(0, T], \\ v_x(0, t) = v_x(l, t) = 0, & t\in (0, T], \\ v|_{t = 0} = \tilde{g}(x), & x\in [0, l], \end{array}\right. \end{equation} $

其中, $ \tilde{a}(x)\ge \Lambda>0 $.通常,齐次Neumann边界条件的处理必须具有二阶精度,否则整体计算精度不能达到二阶.对于方程(1.4),可以使用所谓的虚拟点法^[9],即利用中心差商来近似Neumann边界条件,然后通过联立方程来消除虚拟点.然而,这种方法不能应用于我们的问题.事实上,方程(1.1)在边界处退化为下列两个双曲型方程

(1.5) $ \begin{eqnarray} && \frac{\partial u}{\partial t}-a'(0)\frac{\partial u}{\partial x} = f(0, t), \end{eqnarray} $

(1.6) $ \begin{eqnarray} && \frac{\partial u}{\partial t}-a'(l)\frac{\partial u}{\partial x} = f(l, t). \end{eqnarray} $

如果我们仍然将中心差商应用于方程(1.5)-(1.6),则不能消除虚拟点,因为系数$ a(x) $在$ x = 0 $和$ x = l $时为零.

本文采用一种新的且相当简单的方法来处理方程(1.5)-(1.6),从而得到二阶精度的差分格式,并证明该格式的稳定性和收敛性,这也是本文的主要贡献.

本文的主要结构如下:在第2节中,提出了一种新的二阶精度差分法,并证明了该方法的稳定性和收敛性.在第3节中,将反问题简化为算子方程,并在共轭梯度法的基础上设计了一种数值算法来求解问题.最后一节,给出了一些典型的数值算例来说明反演算法的有效性.

将区域$ \bar{Q} = [0, l]\times[0, T] $划分为$ J\times N $网格,空间步长为$ h = \frac{l}{J} $,时间步长为$ \tau = \frac{T}{N} $.

网格点$ (x_{j}, t_{n}) $定义为

$ x_{j} = jh, \; j = 0, 1, 2, \cdots, J; $

$ t_{n} = n\tau, \; n = 0, 1, 2, \cdots, N. $

记号$ u{_{j}^{n}} $表示有限差分方程的解$ u(jh, n\tau) $.

本文引入以下记号

$ \begin{eqnarray*} &&\delta_{x}u_{i+\frac{1}{2}} = \frac{1}{h}(u_{i+1}-u_{i}), {\quad} \delta_{x}^{2}u_{i} = \frac{1}{h}(\delta_{x}u_{i+\frac{1}{2}}-\delta_{x}u_{i-\frac{1}{2}}), \\ &&D_{x^{+}}u_{i} = \frac{1}{h}(u_{i+1}-u_{i}), {\quad} D_{x^{-}}u_{i} = \frac{1}{h}(u_{i}-u_{i-1}), \\ &&t_{k+\frac{1}{2}} = \frac{1}{2}(t_k+t_{k+1}), \delta_{t}u^{k+\frac{1}{2}} = \frac{1}{\tau}(u^{k+1}-u^{k}), \\ &&B_{x^{+}}u_i = \frac{1}{2h}(-3u_i+4u_{i+1}-u_{i+2}), {\quad} B_{x^{-}}u_i = \frac{1}{2h}(u_{i-2}-4u_{i-1}+3u_i) \end{eqnarray*} $

和一些模

$ \|u\| = \sqrt{h\sum\limits_{j = 1}^{J-1}\alpha_{j}u_{j}^{2}}, \; \; \; \; |[u]| = \sqrt{h\sum\limits_{j = 0}^{J}\alpha_{j}u_{j}^{2}}, $

其中, $ \alpha_{0} = \alpha_{J} = \frac{1}{2} $, $ \alpha_{1} = \alpha_{2} = \cdots = \alpha_{J-1} = 1 $.

通过有限体积法^[9],我们可得方程(1.1)的CN格式

(2.1) $ \begin{equation} \delta_t u_{j}^{n+\frac{1}{2}}-\delta_x\left( a_j\delta_x u_{j}^{n+\frac{1}{2}}\right) = f_{j}^{n+\frac{1}{2}}, \end{equation} $

其中, $ 1\leq j\leq J-1 $, $ 0\leq n\leq N-1 $, $ a_j = a(x_j) $.上式的截断误差为$ O(\tau^2+h^2) $.

本文假设$ a'(0), \; a'(l)\neq 0 $.因此,边界条件由方程(1.5)-(1.6)给出.为了保持二阶精度,我们用以下差分方程

(2.2) $ \begin{eqnarray} && \delta_t u_{0}^{n+\frac{1}{2}}-a'(0)B_{x^{+}}u_{0}^{n+\frac{1}{2}} = f_{0}^{n+\frac{1}{2}}, \end{eqnarray} $

(2.3) $ \begin{eqnarray} && \delta_t u_{J}^{n+\frac{1}{2}}-a'(l)B_{x^{-}}u_{J}^{n+\frac{1}{2}} = f_{J}^{n+\frac{1}{2}} \end{eqnarray} $

来近似方程(1.5)-(1.6).容易看出, (2.2)和(2.3)式的截断误差是$ O(\tau^2+h^2) $.

方程(1.1)的初始条件可以离散为

(2.4) $ \begin{equation} u_{j}^{0} = g_{j}, \; \; \; \; \; \; j = 0, 1, 2, \cdots, J. \end{equation} $

引理2.1 假设$ {\{u_{j}^{n}|\; 0\leq j\leq J, \; 0\leq n\leq N\}} $是差分方程(2.1)-(2.4)的解,那么当$ \tau $较小时,有

$ |[u^{n}]|^{2}\leq {\rm e}^{4CT}\left(|[g]|^{2}+4T\max\limits_{0\leq k\leq n-1}|[f^{k+\frac{1}{2}}]|^{2}\right), \; \; n = 1, 2, \cdots, N, $

这里, $ C $与$ a(x) $有关.

证 在方程(2.1)两边同时乘$ 2hu_{j}^{n+\frac{1}{2}} $,并从$ j = 1 $到$ j = J-1 $进行加和,得到

(2.5) $ \begin{equation} \frac{1}{\tau}(\|u^{n+1}\|^{2}-\|u^{n}\|^{2}) = 2h\sum\limits_{j = 1}^{J-1} [\delta_{x}(a_{j}\delta_{x}u_{j}^{n+\frac{1}{2}})]u_{j}^{n+\frac{1}{2}}+2h\sum\limits_{j = 1}^{J-1} f_{j}^{n+\frac{1}{2}}u_{j}^{n+\frac{1}{2}}. \end{equation} $

由(2.5)式右端的第一项,我们可知

(2.6) $ \begin{eqnarray} && 2h\sum\limits_{j = 1}^{J-1}\left[\delta_{x}(a_{j}\delta_{x}u_{j}^{n+\frac{1}{2}})\right]u_{j}^{n+\frac{1}{2}} \\ & = & 2\sum\limits_{j = 1}^{J-1}\left[a_{j+\frac{1}{2}}\delta_{x}u_{j+\frac{1}{2}}^{n+\frac{1}{2}}-a_{j-\frac{1}{2}}\delta_{x}u_{j-\frac{1}{2}}^{n+\frac{1}{2}}\right]u_{j}^{n+\frac{1}{2}}\\ & = & 2\sum\limits_{j = 2}^{J}\left(a_{j-\frac{1}{2}}\delta_{x}u_{j-\frac{1}{2}}^{n+\frac{1}{2}}\right)u_{j-1}^{n+\frac{1}{2}}-2\sum\limits_{j = 1}^{J-1}\left(a_{j-\frac{1}{2}}\delta_{x}u_{j-\frac{1}{2}}^{n+\frac{1}{2}}\right) u_{j}^{n+\frac{1}{2}}\\ & = & -2\sum\limits_{j = 1}^{J}\left(a_{j-\frac{1}{2}}\delta_{x}u_{j-\frac{1}{2}}^{n+\frac{1}{2}}\right) \left(u_{j}^{n+\frac{1}{2}}-u_{j-1}^{n+\frac{1}{2}}\right) +2\left(a_{J-\frac{1}{2}}\delta_{x}u_{J-\frac{1}{2}}^{n+\frac{1}{2}}\right)u_{J}^{n+\frac{1}{2}}-2\left(a_{\frac{1}{2}}\delta_{x}u_{\frac{1}{2}}^{n+\frac{1}{2}}\right)u_{0}^{n+\frac{1}{2}} \\ & = &-2h\sum\limits_{j = 1}^{J}a_{j-\frac{1}{2}}\left|\delta_{x}u_{j-\frac{1}{2}}^{n+\frac{1}{2}}\right|^2 +2\left(a_{J-\frac{1}{2}}D_{x-}u_{J}^{n+\frac{1}{2}}\right)u_{J}^{n+\frac{1}{2}}-2\left(a_{\frac{1}{2}}D_{x+}u_{0}^{n+\frac{1}{2}}\right)u_{0}^{n+\frac{1}{2}} . \end{eqnarray} $

结合(2.5)式、(2.6)式以及柯西不等式可得

(2.7) $ \begin{eqnarray} &&\frac{1}{\tau}\left(\left\|u^{n+1}\right\|^{2}-\left\|u^{n}\right\|^{2}\right) +2h\sum\limits_{j = 1}^{J}a_{j-\frac{1}{2}}\left|\delta_{x}u_{j-\frac{1}{2}}^{n+\frac{1}{2}}\right|^{2} \\ &\leq& 2\left(a_{J-\frac{1}{2}}D_{x^{-}}u_{J}^{n+\frac{1}{2}}\right)u_{J}^{n+\frac{1}{2}}- 2\left(a_{\frac{1}{2}}D_{x^{+}}u_{0}^{n+\frac{1}{2}}\right)u_{0}^{n+\frac{1}{2}} +\left\|u^{n+\frac{1}{2}}\right\|^{2}+\left\|f^{n+\frac{1}{2}}\right\|^{2}. \end{eqnarray} $

在方程(2.2)的两边同时乘$ u_{0}^{n+\frac{1}{2}}h $,得到

(2.8) $ \begin{eqnarray} \frac{1}{2\tau}\left[(u_{0}^{n+1})^{2}h-(u_{0}^{n})^{2}h\right] & = & a'(0)\left(B_{x^{+}}u_{0}^{n+\frac{1}{2}}\right)u_{0}^{n+\frac{1}{2}}h+ f_{0}^{n+\frac{1}{2}}u_{0}^{n+\frac{1}{2}}h \\ &\leq& a'(0)\left(B_{x^{+}}u_{0}^{n+\frac{1}{2}}\right)u_{0}^{n+\frac{1}{2}}h+ \frac{h}{2}\left(\left|f_{0}^{n+\frac{1}{2}}\right|^2+\left|u_{0}^{n+\frac{1}{2}}\right|^2\right). \end{eqnarray} $

对方程(2.3)做类似的处理,有

(2.9) $ \begin{equation} \frac{1}{2\tau}\left[(u_{J}^{n+1})^{2}h-(u_{J}^{n})^{2}h\right] \leq a'(l)\left(B_{x^{-}}u_{J}^{n+\frac{1}{2}}\right)u_{J}^{n+\frac{1}{2}}h+ \frac{h}{2}\left(\left|f_{J}^{n+\frac{1}{2}}\right|^2+\left|u_{J}^{n+\frac{1}{2}}\right|^2\right). \end{equation} $

由(2.7)-(2.9)式,我们可以得到

(2.10) $ \begin{eqnarray} && \frac{1}{\tau}\left(|[u^{n+1}]|^{2}-|[u^{n}]|^{2}\right) +2h\sum\limits_{j = 1}^{J}a_{j-\frac{1}{2}}\left|\delta_{x}u_{j-\frac{1}{2}}^{n+\frac{1}{2}}\right|^{2} \\ &\leq& |[u^{n+\frac{1}{2}}]|^{2}+|[f^{n+\frac{1}{2}}]|^{2}+ 2\left(a_{J-\frac{1}{2}}D_{x^{-}}u_{J}^{n+\frac{1}{2}}\right)u_{J}^{n+\frac{1}{2}} -2\left(a_{\frac{1}{2}}D_{x^{+}}u_{0}^{n+\frac{1}{2}}\right)u_{0}^{n+\frac{1}{2}} \\ &&+a'(0)\left(B_{x^{+}}u_{0}^{n+\frac{1}{2}}\right)u_{0}^{n+\frac{1}{2}}h+a'(l)\left(B_{x^{-}}u_{J}^{n+\frac{1}{2}}\right)u_{J}^{n+\frac{1}{2}}h. \end{eqnarray} $

由$ a(x) $的光滑性,利用Taylor展式可以将其展开成如下形式

(2.11) $ \begin{eqnarray} &&a_{\frac{1}{2}} = a(\frac{1}{2}h) = a(0)+a'(0)\frac{h}{2}+\frac{1}{2}a''(\theta_{1})\frac{h^{2}}{4} = a'(0)\frac{h}{2}+\frac{1}{2}a''(\theta_{1})\frac{h^{2}}{4}, \end{eqnarray} $

(2.12) $ \begin{eqnarray} &&a_{J-\frac{1}{2}} = a(J h-\frac{1}{2}h) = a(l)-a'(l)\frac{h}{2}+\frac{1}{2}a''(\theta_{2})\frac{h^{2}}{4} = -a'(l)\frac{h}{2}+\frac{1}{2}a''(\theta_{2})\frac{h^{2}}{4}, \end{eqnarray} $

其中, $ 0\leq \theta_{1}\leq \frac{1}{2}h $, $ (J-\frac{1}{2})h\leq\theta_{2}\leq J h $.

由(2.10)式、(2.11)式以及(2.12)式可知

(2.13) $ \begin{eqnarray} && \frac{1}{\tau}\left(|[u^{n+1}]|^{2}-|[u^{n}]|^{2}\right) +2h\sum\limits_{j = 1}^{J}a_{j-\frac{1}{2}}\left|\delta_{x}u_{j-\frac{1}{2}}^{n+\frac{1}{2}}\right|^{2} \\ &\leq& |[u^{n+\frac{1}{2}}]|^{2}+|[f^{n+\frac{1}{2}}]|^{2} \\ &&+a'(0)\left[(B_{x^{+}}-D_{x^{+}}) u_{0}^{n+\frac{1}{2}}\right]u_{0}^{n+\frac{1}{2}}h +a'(l) \left[(B_{x^{-}}-D_{x^{-}})u_{J}^{n+\frac{1}{2}}\right]u_{J}^{n+\frac{1}{2}}h\\ &&+\frac{1}{4}a''(\theta_{2})\left(D_{x^{-}}u_{J}^{n+\frac{1}{2}}\right)u_{J}^{n+\frac{1}{2}}h^{2}- \frac{1}{4}a''(\theta_{1})\left(D_{x^{+}}u_{0}^{n+\frac{1}{2}}\right)u_{0}^{n+\frac{1}{2}}h^{2}. \end{eqnarray} $

将(2.13)式右端的第三项和第四项分别用$ I_1 $和$ I_2 $表示.对于$ I_1 $,我们利用(2.1)式有

(2.14) $ \begin{eqnarray} I_1 & = & a'(0)u_{0}^{n+\frac{1}{2}}h\left[\frac{1}{2h}(-3u_{0}^{n+\frac{1}{2}} +4u_{1}^{n+\frac{1}{2}}-u_{2}^{n+\frac{1}{2}})-\frac{1}{h}(u_{1}^{n+\frac{1}{2}}- u_{0}^{n+\frac{1}{2}})\right] \\ & = & -\frac{1}{2}h^2a'(0)u_{0}^{n+\frac{1}{2}}\delta_x^2u_{1}^{n+\frac{1}{2}} \\ & = & -\frac{1}{2}\frac{a'(0)}{a_1}h^2\delta_x(a_1\delta_xu_{1}^{n+\frac{1}{2}})u_{1}^{n+\frac{1}{2}} +\frac{1}{2}\frac{a'(0)}{a_1}\left[(a_{\frac{3}{2}}-a_1)u_{2}^{n+\frac{1}{2}}\right. \\ &&\left.-(a_{\frac{3}{2}}+a_{\frac{1}{2}}-2a_1)u_{1}^{n+\frac{1}{2}}+ (a_{\frac{1}{2}}-a_1)u_{0}^{n+\frac{1}{2}}\right]u_{0}^{n+\frac{1}{2}} \\ & = & \frac{1}{2}\frac{a'(0)}{a_1}h^2(f_{1}^{n+\frac{1}{2}}-\delta_tu_{1}^{n+\frac{1}{2}})u_{0}^{n+\frac{1}{2}} \\ &&+\frac{1}{2}\frac{a'(0)}{a_1}\left[(a_{\frac{3}{2}}-a_1)u_{2}^{n+\frac{1}{2}} -(a_{\frac{3}{2}}+a_{\frac{1}{2}}-2a_1)u_{1}^{n+\frac{1}{2}}+ (a_{\frac{1}{2}}-a_1)u_{0}^{n+\frac{1}{2}}\right]u_{0}^{n+\frac{1}{2}}, \end{eqnarray} $

注意到

(2.15) $ \begin{eqnarray} &&a_{\frac{3}{2}} = a_1+\frac{h}{2}a'_1+\frac{1}{2}a''(\theta_{3})\frac{h^{2}}{4}, \end{eqnarray} $

(2.16) $ \begin{eqnarray} &&a_{\frac{1}{2}} = a_1-\frac{h}{2}a'_1+\frac{1}{2}a''(\theta_{4})\frac{h^{2}}{4}, \end{eqnarray} $

这里, $ h\leq \theta_{3}\leq \frac{3}{2}h $, $ \frac{h}{2}\leq \theta_{4}\leq h $.结合(2.14)-(2.16)式,得到

(2.17) $ \begin{eqnarray} I_1 & = & \frac{h^2}{2}\frac{a'(0)}{a_1}(f_{1}^{n+\frac{1}{2}}-\delta_tu_{1}^{n+\frac{1}{2}})u_{0}^{n+\frac{1}{2}} +\frac{1}{2}\frac{a'(0)}{a_1}\left[(\frac{h}{2}a'_1+\frac{h^2}{8}a''(\theta_{3}))u_{2}^{n+\frac{1}{2}}\right. \\ && \left.-\frac{h^2}{8}(a''(\theta_{3})+a''(\theta_{4}))u_{1}^{n+\frac{1}{2}}+ (-\frac{h}{2}a'_1+\frac{h^2}{8}a''(\theta_{4}))u_{0}^{n+\frac{1}{2}}\right]u_{0}^{n+\frac{1}{2}}. \end{eqnarray} $

利用$ a(x) $的光滑性,令

(2.18) $ \begin{equation} C_1 = \frac{1}{4}\left|\frac{a'(0)}{a_1}\right|\max\left\{1, \; \; |a'_1|, \; \; \frac{1}{4} |a''(\theta_{3})|, \; \; \frac{1}{4} |a''(\theta_{4})|\right\}. \end{equation} $

因此, (2.17)式有如下估计

(2.19) $ \begin{eqnarray} I_1 &\leq& C_1h^2\left[|f_{1}^{n+\frac{1}{2}}|^2+|u_{0}^{n+\frac{1}{2}}|^2 +\frac{1}{\tau}\left(|u_{1}^{n+1}|^2+|u_{1}^{n}|^2+2|u_{0}^{n+\frac{1}{2}}|^2\right)\right] \\ &&+C_1h\left[(1+h)|u_{2}^{n+\frac{1}{2}}| +2h|u_{1}^{n+\frac{1}{2}}|+ (1+h)|u_{0}^{n+\frac{1}{2}}|\right] |u_{0}^{n+\frac{1}{2}}| \\ &\leq& C_1h|[f^{n+\frac{1}{2}}]|^2+\frac{C_1h}{\tau}\left(|[u^{n+1}]|^2+|[u^{n}]|^2\right) +C_1\left(4+h+\frac{2h}{\tau}\right)|[u^{n+\frac{1}{2}}]|^2 \\ &\leq& C_1h|[f^{n+\frac{1}{2}}]|^2 +C_1\left(2+\frac{h}{2}+\frac{2h}{\tau}\right)\left(|[u^{n+1}]|^2+|[u^{n}]|^2\right), \end{eqnarray} $

这里用到了如下不等式

(2.20) $ \begin{equation} |[u^{n+\frac{1}{2}}]|^2\leq \frac{1}{2}\left(|[u^{n+1}]|^2+|[u^{n}]|^2\right). \end{equation} $

对$ I_2 $做类似的处理,可得

(2.21) $ \begin{eqnarray} I_2 \leq C_2h|[f^{n+\frac{1}{2}}]|^2 +C_2\left(2+\frac{h}{2}+\frac{2h}{\tau}\right)\left(|[u^{n+1}]|^2+|[u^{n}]|^2\right), \end{eqnarray} $

其中

$ C_2 = \frac{1}{4}\left|\frac{a'(l)}{a_{J-1}}\right|\max\left\{1, \; \; |a'_{J-1}|, \; \; \frac{1}{4} |a''(x)|\right\}. $

对于方程(2.13)右端的最后两项,我们可以得到

(2.22) $ \begin{eqnarray} && \frac{1}{4}a''(\theta_{2})\left(D_{x^{-}}u_{J}^{n+\frac{1}{2}}\right)u_{J}^{n+\frac{1}{2}}h^{2}- \frac{1}{4}a''(\theta_{1})\left(D_{x^{+}}u_{0}^{n+\frac{1}{2}}\right)u_{0}^{n+\frac{1}{2}}h^{2} \\ &\leq& C_3h\left[|u_{J}^{n+\frac{1}{2}}(u_{J}^{n+\frac{1}{2}}-u_{J-1}^{n+\frac{1}{2}})| +|u_{0}^{n+\frac{1}{2}}(u_{1}^{n+\frac{1}{2}}-u_{0}^{n+\frac{1}{2}})|\right] \\ &\leq& 3C_3|[u^{n+\frac{1}{2}}]|^2 \\ &\leq& \frac{3}{2}C_3\left(|[u^{n+1}]|^2+|[u^{n}]|^2\right), \end{eqnarray} $

其中$ C_3 = \frac{1}{4}\max\left\{|a''(\theta_1)|, \; \; |a''(\theta_2)|\right\} $.

结合(2.13), (2.19), (2.21)和(2.22)式,可知

(2.23) $ \begin{eqnarray} && \frac{1}{\tau}\left(|[u^{n+1}]|^{2}-|[u^{n}]|^{2}\right)-(1+(C_1+C_2)h)|[f^{n+\frac{1}{2}}]|^2 \\ &\leq&\left[\frac{1}{2}+\frac{3}{2}C_3+(C_1+C_2)\left(2+\frac{h}{2}+\frac{2h}{\tau}\right)\right] \left(|[u^{n+1}]|^2+|[u^{n}]|^2\right). \end{eqnarray} $

在实际计算过程中,参数$ \tau $和$ h $通常具有相同阶数,亦即$ \tau\sim h $.因此,在不失一般性的前提下,我们可以假设

(2.24) $ \begin{equation} 1+(C_1+C_2)h\leq 2, \; \; \; \; \frac{1}{2}+\frac{3}{2}C_3+(C_1+C_2)\left(2+\frac{h}{2}+\frac{2h}{\tau}\right)\leq C. \end{equation} $

然后,可以将(2.23)式改写为

(2.25) $ \begin{equation} |[u^{n+1}]|^{2}\leq\frac{1+C\tau}{1-C\tau}|[u^{n}]|^{2}+\frac{2\tau}{1-C\tau}|[f^{n+\frac{1}{2}}]|^{2}. \end{equation} $

因此,如果$ \tau $足够小,以至于$ \tau<\frac{1}{2C} $,那么有

(2.26) $ \begin{eqnarray} \frac{1}{1-C\tau}<1+2C\tau, \; \; \; \; \frac{1+C\tau}{1-C\tau}<1+4C\tau, \; \; \; \; \frac{2\tau}{1-C\tau}<4\tau. \end{eqnarray} $

由(2.25)和(2.26)式,我们可知

(2.27) $ \begin{eqnarray} |[u^{n+1}]|^{2}\leq \left(1+4C\tau\right)|[u^{n}]|^{2}+4\tau|[f^{n+\frac{1}{2}}]|^{2}. \end{eqnarray} $

利用离散Gronwall不等式^[12],可以得到

$ \begin{eqnarray*} |[u^{n}]|^{2} &\leq & {\rm e}^{4Cn\tau}\left(|[u^{0}]|^{2}+4\tau\sum\limits_{k = 0}^{n-1}|[f^{k+\frac{1}{2}}]|^{2}\right) \\ &\leq& {\rm e}^{4CT}\left(|[g]|^{2}+4T\max\limits_{0\leq k \leq n-1}|[f^{k+\frac{1}{2}}]|^{2}\right). \end{eqnarray*} $

引理2.1证明完毕.

现在,我们讨论差分格式的收敛性.设

$ z_j^{n+\frac{1}{2}} = u(x_j, t_{n+\frac{1}{2}})-u_j^{n+\frac{1}{2}}, \; \; \; \; 0\leq j\leq J, \; 0\leq n\leq N-1. $

可以很容易地看出, $ z_j^{n+\frac{1}{2}} $满足以下误差方程

(2.28) $ \begin{eqnarray} \delta_{t}z_{j}^{n+\frac{1}{2}}-\delta_{x}(a_{j}\delta_{x}z_{j}^{n+\frac{1}{2}})& = &e_{j}^{n+\frac{1}{2}}, 1\leq j\leq J-1, 0\leq n\leq N-1, \end{eqnarray} $

(2.29) $ \begin{eqnarray} z_{j}^{0}& = &0, \qquad{\quad}\ \ 0\leq j\leq J, \end{eqnarray} $

(2.30) $ \begin{eqnarray} \delta_{t}z_{0}^{n+\frac{1}{2}}-a'(0)B_{x^{+}}z_{0}^{n+\frac{1}{2}}& = &e_{0}^{n+\frac{1}{2}}, 0\leq n\leq N-1, \end{eqnarray} $

(2.31) $ \begin{eqnarray} \delta_{t}z_{J}^{n+\frac{1}{2}}-a'(l)B_{x^{-}}z_{J}^{n+\frac{1}{2}}& = &e_{J}^{n+\frac{1}{2}}, 0\leq n\leq N-1. \end{eqnarray} $

值得注意的是

$ e_{j}^{n+\frac{1}{2}} = O(\tau^2+h^2), \qquad 1\leq j\leq J, \; 0\leq n\leq N-1. $

通过引理2.1,我们可以得到

(2.32) $ \begin{equation} |[u(\cdot, t_{n})-u^{n}]| = O(\tau^2)+O(h^{\frac{5}{2}}), \; \; 0\leq n\leq N. \end{equation} $

目前存在许多有效的正则化方法,例如Tikhonov正则化方法或Landweber迭代,它们都可用于反问题(1.1)的求解.然而, Tikhonov正则化方法需要求解抽象算子方程的逆算子,这通常是很困难的. Landweber迭代可以避免这一困难,但其收敛速度非常慢.所以,本文采用共轭梯度法(CGM) (参见文献[5])来处理我们的反问题.

定义下列算子

(3.1) $ \begin{eqnarray} {\cal L}:\; \; L^2(0, l) &\rightarrow& L^2(0, l) \\ {\cal L}g & = & u(\cdot, T) = k(x), \end{eqnarray} $

其中, $ u $是方程(1.1)的解.容易看出, $ f(x, t)\neq 0 $,算子$ {\cal L} $不是线性算子,而是仿射算子.利用线性迭加原理,我们可以将观测值$ k(x) $分解成两个函数$ k_1(x) $和$ k_2(x) $,它们满足$ k_1(x)+k_2(x) = k(x) $.将函数$ k_1(x) $定义为$ u_1(\cdot, T) = k_1(x) $,其中$ u_1 $满足以下方程

(3.2) $ \begin{equation} \left\{\begin{array}{ll} u_{1t}-(a(x)u_{1x})_x = 0, \quad & (x, t)\in Q, \\ u_1|_{t = 0} = g(x), & x\in [0, l]. \end{array}\right. \end{equation} $

将函数$ k_2(x) $定义为$ u_2(\cdot, T) = k_2(x) $,其中$ u_2 $满足以下方程

(3.3) $ \begin{equation} \left\{\begin{array}{ll} u_{2t}-(a(x)u_{2x})_x = f(x, t), \quad & (x, t)\in Q, \\ u_2|_{t = 0} = 0, & x\in [0, l]. \end{array}\right. \end{equation} $

函数$ g(x) $未知,而函数$ f(x, t) $是给定的.因此,方程(3.3)是一个适定的正问题,且$ k_2(x) $可以看作是一个已知函数.如果我们定义下列算子

(3.4) $ \begin{eqnarray} {\cal L}_1:\; \; L^2(0, l) &\rightarrow& L^2(0, l) \\ {\cal L}_1g & = & u_1(\cdot, T) = k_1(x), \end{eqnarray} $

其中$ u_1 $是方程(3.2)的解,则$ {\cal L}_1 $是线性算子.

因此,基于上述的分析,我们在本节始终假设$ f(x, t)\equiv 0, \; (x, t)\in Q $.算子$ {\cal L} $是线性的,其共轭算子$ {\cal L}^* $由下面引理给出.

引理3.1 对于任意$ \psi(x) $,令$ v(\cdot, 0) = {\cal L}^*\psi $.那么$ v $满足下列抛物型方程

(3.5) $ \begin{equation} \left\{\begin{array}{ll} -v_t-(a(x)v_x)_x = 0, \quad & (x, t)\in Q, \\ v|_{t = T} = \psi(x), & x\in \Omega. \end{array}\right. \end{equation} $

引理3.1的证明见文献[16].

假设“真解”$ k(x) $是可以达到的,即存在$ g(x)\in L^2(0, l) $,使得

$ u(x, T;g) = k(x), $

而且观测噪声水平$ \|k^{\delta}-k\|_{L^2(0, l)}\leq \delta $的上界$ \delta $是已知的.

迭代算法的过程可以表述为如下步骤.

Step 1 令$ m = 0 $,选择迭代初值$ g = g_{0}(x) $,为方便起见,我们选取$ g_{0}(x)\equiv0, \; \; x\in[0, l] $.

Step 2 求解初边值问题(1.1),得到解$ u_{m}(x, t) $,其中$ g(x) = g_{m}(x) $.

Step 3 确定残差

$ r_m = k^{\delta}(x)-u_m(x, T). $

然后,求解共轭方程

(3.6) $ \begin{equation} \left\{\begin{array}{ll} -v_t-(a(x)v_x)_x = 0, \quad & (x, t)\in Q, \\ v|_{t = T} = r_m(x), \\ \end{array}\right. \end{equation} $

得到解$ v_m(x, 0) $.

Step 4 计算

$ s_m = v_m(\cdot, 0)+\alpha_{m-1}s_{m-1}, $

其中

$ \alpha_{m-1} = \left\{\begin{array}{ll} 0, \quad &m = 0, \\ { }\frac{\|v_m(\cdot, 0)\|^2_{L^2(0, l)}}{\|v_{m-1}(\cdot, 0)\|^2_{L^2(0, l)}}, {\quad}& m\ge 1. \end{array}\right. $

Step 5 求解以下方程

(3.7) $ \begin{equation} \left\{\begin{array}{ll} u_t-(a(x)u_x)_x = 0, {\quad} (x, t)\in Q, \\ u(x, 0) = s_m(x), \\ \end{array}\right. \end{equation} $

得到解$ u(x, T): = q_m(x) $.计算

$ \beta_{m} = \frac{\|v_m(\cdot, 0)\|^2_{L^2(0, l)}}{\|q_{m}\|^2_{L^2(0, l)}}, $

并令

$ g_{m+1} = g_m+\beta_{m}s_m. $

Step 6 令$ m = m+1 $,继续执行Step 2.

终止迭代步骤如下.

设$ \lambda>1 $是一个定数.直到第$ m\in {\Bbb N} $步时终止算法,此时

(3.8) $ \begin{equation} \|r_m\|_{L^2(0, l)}\leq \lambda \delta. \end{equation} $

首先,我们检验差分格式对第二节中正问题的有效性.

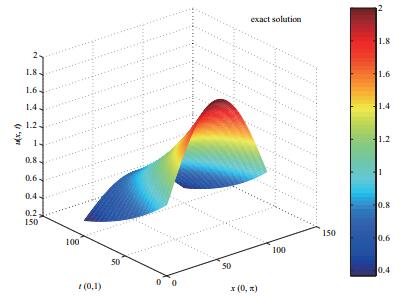
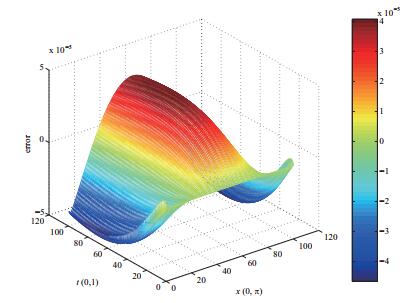
我们先考虑以下方程

(4.1) $ \begin{equation} \left\{\begin{array}{ll} u_t-(\sin(x)u_x)_x = -{\rm e}^{-t}(1+\sin(x)+\cos(2x)), \quad & (x, t)\in [0, \pi]\times(0, 1], \\ u|_{t = 0} = 1+\sin(x), & x\in [0, \pi], \end{array}\right. \end{equation} $

其中$ f(x, t) = -{\rm e}^{-t}(1+\sin(x)+\cos(2x)) $为源项,在这种情况下, $ u(x, t) = {\rm e}^{-t}(1+\sin(x)) $为方程(4.1)的解析解.在数值计算过程中,我们取空间步长$ h $和时间步长$ \tau $为

$ h = \pi/100, \; \tau = 0.01. $

图 1和图 2分别表示精确解$ u(x, t) $和差分格式(2.1)-(2.4)的误差面.可以很容易地看出,数值结果与第二节中的理论精度吻合得很好.

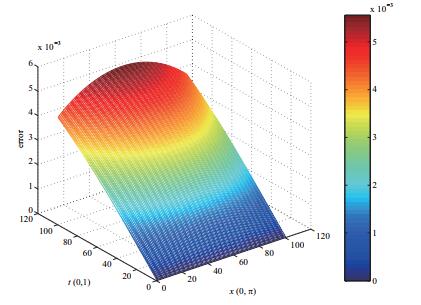
其后,我们考虑文献[16]中所提出的差分格式

(4.2) $ \begin{eqnarray} \delta_{t}u_{j}^{n+\frac{1}{2}}-\delta_{x}(a_{j}\delta_{x}u_{j}^{n+1})& = &f_{j}^{n+1}, \qquad 1\leq j\leq J-1, \; 0\leq n\leq N-1, \end{eqnarray} $

(4.3) $ \begin{eqnarray} u_{j}^{0}& = &g_{j}, {\quad}\ \qquad 0\leq j\leq J, \end{eqnarray} $

(4.4) $ \begin{eqnarray} \delta_{t}u_{0}^{n+\frac{1}{2}}-a'(0)D_{x^{+}}u_{0}^{n+1}& = &f_{0}^{n+1}, \qquad 0\leq n\leq N-1, \end{eqnarray} $

(4.5) $ \begin{eqnarray} \delta_{t}u_{J}^{n+\frac{1}{2}}-a'(l)D_{x^{-}}u_{J}^{n+1}& = &f_{J}^{n+1}, \qquad 0\leq n\leq N-1, \end{eqnarray} $

其截断误差为$ O(\tau+h) $. 图 3表示该差分格式的误差面.

将图 2和图 3相比较,我们可以得知差分格式(4.2)-(4.5)具有一阶精度,而差分格式(2.1)-(2.4)具有二阶精度,这与上述理论结果是一致的.

接下来,我们转而进行反问题的数值模拟.我们做了两个数值算例来检验迭代算法的稳定性.在所有算例中,基本参数选取为

$ l = \pi, \; \; T = 0.2, \; \; f(x, t)\equiv 0, \; (x, t)\in Q, $

并且假设扩散系数$ a(x) $为

$ a(x) = \sin (x), \; \; x\in [0, \pi]. $

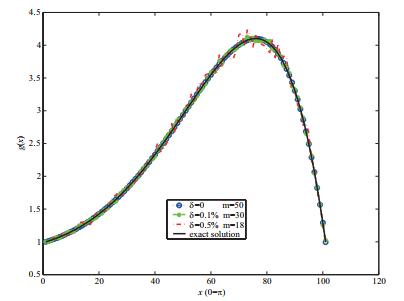
算例1 第一个算例中,我们取

$ g(x) = 1+2\sin (x)\exp\left(x-\frac{\pi}{2}\right), \; \; x\in[0, \pi]. $

附加条件$ k(x) $由下式给出

$ k(x) = u(x, T;g), \; \; x\in[0, \pi], $

$ u(x, t;g) $为(1.1)对应于初值$ g(x) $和$ f\equiv0 $的数值解.引入如下形式的噪声数据

$ k^{\delta}(x) = u^{\delta}(x, T) = u(x, T)[1+\delta\times {\rm random}(x)]. $

图 4展示了引入噪声数据下的重构结果.当$ \delta = 0 $时, (即使在这种情况下,附加数据仍然存在误差,因为它们是根据正问题计算得出的)未知初值函数$ g(x) $可以快速地被重构并且过程稳定.迭代初值取为0,我们看到,仅需要50次迭代就可以很好地重构初值.在噪声水平为$ \delta = 0.1\% $以及$ \delta = 0.5\% $的情况下,重构结果也是令人满意的.虽然存在一些震荡现象,但该算法还是稳定有效的.

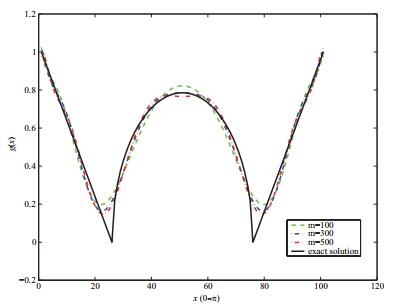
算例2 在第二个数值实验中,我们试图重构一个较复杂的函数$ g(x) $,令其为

(4.6) $ \begin{equation} g(x) = \left\{\begin{array}{ll} { } -\frac{\pi}{4}\left(x-\frac{\pi}{4}\right), &{ } x\in \left[0, \frac{\pi}{4}\right], \\ { } \left[\frac{\pi^2}{16}-\left(x-\frac{\pi}{2}\right)^2\right]^{\frac{1}{2}}, \quad & { } x\in \left[\frac{\pi}{4}, \frac{3\pi}{4}\right], \\ { } \frac{\pi}{4}\left(x-\frac{3\pi}{4}\right), &{ } x\in \left[\frac{3\pi}{4}, \pi\right], \end{array}\right. \end{equation} $

该函数是连续阶跃函数.这里的$ a(x) $与算例1中的函数相同.

虽然该函数是连续函数,但很明显它在一些点是不可微的.这些不可微点在数学中称为尖点.可以看出,该函数的两个连接点$ x = \frac{\pi}{4} $和$ x = \frac{3\pi}{4} $是尖点.在反问题的计算中,精确重构尖点是很困难的.

该算法效果良好,只需要100次迭代,就可以达到令人满意的收敛结果.如果继续增加迭代次数,那么数值曲线会更加接近尖点.需说明一下, 500次迭代并不算太多.事实上,如果采用Landweber迭代^[16],为了达到同样的效果,所需的迭代次数约为当前算法的10倍.