为了顺利应用非线性连续模型研究生物种群的演化趋势,数值求解是关键环节之一,因为绝大多数情况下无法获得封闭的精确解.种群内部的个体之间存在诸如年龄、尺度、等级、生理阶段等差异,而结构化的种群模型能将个体的生命参数与种群演化动力学联系起来,这类模型的连续形式通常为非线性偏微分－积分方程（组）.受人口动力学研究的启发,自上个世纪80年代学者们开始研究种群生态学领域连续型结构化种群模型的数值方法,取得了一些可用性很好的结果.年龄结构模型可参见文献[1-8]及其所引文献;尺度结构模型可参见文献[9-17]及所引文献.以下简要回顾一些主要成果.

文献[1]对一类非线性年龄结构模型提出迎风差分近似算法,模型带有广泛的边界条件.运用抽象离散化理论分析了算法的一致性、稳定性与收敛性.文献[2]对同一模型给出盒子算法,它是二阶收敛的.针对Gurtin-MacCamy模型,文献[3]设计Euler方法,但无收敛性分析.文献[4]对McKendrick类模型的最优控制问题导出HJB方程,并对作为其粘性解的值函数提出有限差分法.文献[5]对当时已有的数值方法作综述,主要包括特征线方法与有限差分法.文献[6]就线性自治年龄结构模型给出有限元方法,分析其稳定性并估计误差.基于特征线上的积分,文献[7]为一类非线性非自治系统提出了数值算法,证明其为二阶收敛的.专著[8]对年龄结构系统模型的数值解方法论和具体算法做了可读性很强的陈述.在尺度结构模型方面,文献[9]提出了求解一类随机模型反问题的计算方法,文献[10]对一类具有广泛边界条件的系统证明了解的存在性、光滑性,以及数值解法的收敛性.基于非负增长率和密度依赖的个体参数建模,文献[11]比较了Euler法、隐差分法和特征线法,指出:将特征线法与适应性格点相结合会取得更好的效果.文献[12]对含有正增长率的线性模型提出近似解法,并导出最优收敛速度.类似地,文献[13]研究各种算法的效率,比较特征线法、L-W方法与盒子法,认为盒子法所受限制虽少,但耗时较多.综述文献[14]对当时已有的尺度结构模型的近似算法作出比较和评述.针对描述Gambussia affinis种群演化模型,文献[15]介绍了四种算法,分析解的特点.文献[16]的建模考虑资源与种群的相互作用,并且尺度能收缩、最大尺度可变,文中给出了改进的Euler法.文献[17]对一类含有外界幼体投放的非线性模型设计了隐差分逼近,确立了收敛性.除了分析适定性、稳定性和最优收获问题,文献[18]也对一类尺度结构模型给出了离散化方法与算例.

相比之下,尽管对个体等级现象的生态学研究在上世纪30年代已有成果报道,但对等级结构种群模型的数值方法研究则较晚,本世纪初方才起步.文献[19]对基于尺度的等级结构模型证明了迎风差分逼近的收敛性,以此确立精确解的存在性;该模型的5阶WENO算法则由文献[20]给出.文献[21]引入一类基于特征线的数值逼近法,并给出应用实例.

基于个体等级的连续数学模型,一方面较为真实地描述了种群生态实际,另一方面也导致了较强的理论与数值分析挑战.与年龄、尺度结构模型比较,等级结构模型具有更强的非线性需要处理.适用于年龄和尺度结构模型的数值解法,都不能直接用于等级结构模型.因此,本文拟研究一类连续等级结构模型,提出它的数值解法,证明其收敛性,并给出数值算例.

本文旨在研究下列非线性等级结构种群模型的数值解法:

其中$Q_T = ({0, A}) \times ({0, T})$, $A$为个体的年龄上限, $T$代表种群演化时间长度. $x(a, t)$表述$t$时刻种群的年龄分布,函数$\mu$和$\beta$分别给出种群个体的平均死亡率和繁殖率,它们都依赖于种群内部环境$E(x)(a, t)$, $\alpha$代表年长者的折扣系数.从$E(x)$的定义即知:种群内部竞争中年轻者占优.初始分布由$x_0 (a)$给出,满足$x_0(A)=0$.

假定下述基本条件成立:

(A1)   $\beta \in {\cal C}^2([0, A]\times [0, T])$非负有界,关于$E(x)$单调不增且满足局部Lipschitz条件;

(A2)   $\mu \in {\cal C}^2([0, A)\times [0, T])$恒正,关于$E(x)$严格单增、满足局部Lipschitz条件,且对任意$t>0$有$\int_0^A \mu(a, t, 0){\rm d}a=+\infty$.

注2.1  文献[22]已经对系统(2.1)的适定性进行了分析.运用文献[8,定理2.5]的证明思路可以确立:若基本条件(A1)-(A2)成立,则系统(2.1)的解满足$x\in {\cal C}^2([0, A)\times [0, T]),$$x(a, t)\geq 0, ~x(A, t)=0$.

系统(2.1)的解在特征线$a-t=c \ (c$为常数)上满足

对任意给定的$(a_0, t_0)\in Q_T$,存在$h>0$,使得$(a_0+h, t_0+h)\in Q_T$.从而由(3.1)式知

为了陈述算法所需,引进下列记号:

(1)  常数$A^*\in (0, A)$使得死亡率$\mu(a, t, E(x)(a, t))$在$[0, A^*]$上有界.记$f(a, t)=\int_{A^*}^a \mu (r, t, 0){\rm d}r$, $A^*\le a \le A$且$f(A)=\infty$.

(2)  引入一个正整数$J^*$,在$[0, A]$上定义网格步长$h=A^*/J^*$.则年龄总步数为$J=[A/h]$,时间总步数$N=[T/h]$,这里的$[\cdot]$表示向下取.

(3)  记$a_j=jh, 0\le j\le J$, $a_{J^*}=A^*$且$a_J\le A$.记年龄等分中点$a_{j+\frac{1}{2}}=a_j+\frac{h}{2}=(j+\frac{1}{2})h$, $t_n=nh, 0\le n\le N$,记时间等分中点$t_{n+\frac{1}{2}}=t_n+\frac{h}{2}=(n+\frac{1}{2})h$.

(4)  令${\bf X}^n=[X_0^n, X_1^n, \cdots, X_J^n]$,其中$X_j^n$为$x(a_j, t_n), 0\le j \le J, 0\le n \le N$的数值近似,下标$j$代表年龄网格点$a_j$,上标$n$代表时间网格点$t_n$.

(5)  按照(4)中的记号, ${\bf X}^0=[X_0^0, X_1^0, \cdots, X_J^0]$为已知向量,其中$X_j^0=x_0(a_j), 0\le j\le J.$

利用(4)式可定义系统(2.1)的数值算法如下:对$0\le n \le N-1$,

其中${\bf \beta(X^n)}=\beta(a_j, t_n, {\bf Q_h^{**}(X^n)}), 0 \le j\le J$.这里的

年龄等分中点处的近似值定义为:

令步长$h$取值于集合$H=\{A^*/J^*, J^*\in {\Bbb N}\}$, $J=[A/h]$, $N=[T/h]$.对任意$h\in H$定义如下空间:

其中$\mathbb R ^{J+1}$用于考虑在网格点处对理论解的近似;

其中第一项用于考虑初始分布的误差,第二项用于考虑边界点的误差,第三项用于考虑其它节点的误差.显然空间$X_h, Y_h$有相同的维数.

为了测量误差的大小,定义如下范数:

赋予$X_h$空间和$Y_h$空间如下范数:若$\big({\bf V}^0, {\bf V}^1, \cdots, {\bf V}^N\big)\in X_h$,则

若$\big({\bf P}^0, {\bf P}_0, {\bf P}^1, {\bf P}^2, \cdots, {\bf P}^N\big)\in Y_h,$则

令${\bf x}$代表系统$(2.1)$的解,对$\forall h\in H,$

设$M$是一个固定的正常数,记$B_{x_h}({\bf x}_h, Mh)\subset X_h$为以${\bf x}_h$为中心,以$Mh$为半径的开球,定义如下映射:

等号右边的元素定义如下:

对于$0\le n\le N-1,$

其中

易知, $\big({\bf X}^0, {\bf X}^1, \cdots, {\bf X}^N\big)\in X_h$是方程(3.3)-(3.5)的解,当且仅当

在下文中, $C$将代表一个与步长$h$无关的正的常数,其在不同的位置可能取值不同.

引理4.1   假设(A1)-(A4)成立, ${\bf V}^n, {\bf W}^n\in B_{\infty}({\bf x}^n, Mh), 1\le n\le N.$则当$h$充分小时有

证  由(3.6)和(3.8)式知:对于$1\leq n\leq N$有

(4.9)式得证.

同理由$(3.6)$式和假设条件(A3), $\Vert\beta({\bf X}^n)\Vert_{\infty}\le C$知

$(4.10)$式得证.

当$0\le j \le J^*-1$时,由$(4.6)$式可知

当$J^*\le j \le J-1$时,由$(4.7)$式可知

由假设条件(A1)-(A4),不等式$(4.9)$和$||{\bf W}^n||_{\infty}\le C$知,当$0\le j \le J-1, 0\le n \le N-1$时,有

$(4.11)$式得证.

最后,利用$(3.7)$式和不等式$(4.11)$知:对$1\le n\le N-1$,有

$(4.12)$式得证.

定义4.1^[7]   记局部离散误差为${\bf \Gamma}_h({\bf x}_h)\in Y_h$.若$\lim\limits_{h\rightarrow 0}\Vert{\bf \Gamma}_h({\bf x}_h)\Vert_{Y_h}=0,$则称$(4.1)$式是一致的.

引理4.2   若条件(A1)-(A4)成立,则当$h\rightarrow 0$时,局部离散误差满足:

证  记${\bf \Gamma}_h({\bf x}_h)=\big({\bf L}^0, {\bf L}_0, {\bf L}^1, {\bf L}^2\cdots, {\bf L}^n\big)$.首先考虑${\bf L}^{n+1}, 0\le n\le N-1$的上界.由(3.2), (4.4)式和中点积分法则的标准误差知,当$0\le j\le J^*-1$时,有

其中${\bf x}_{j+\frac{1}{2}}^{n+\frac{1}{2}}$是由$(4.6)$和$(4.7)$式计算的,因此不是系统$(2.1)$在$t_{n+\frac{1}{2}}$处的解,由积分规则的收敛性质及$(3.9)$式,当$0\le j\le J^*-1$时,有

所以有

从而当$0\le j\le J^*-1$时,有$\big|L_{j+1}^{n+1}\big|\le Ch^2$.

同理,当$J^*\le j\le J-1$时,由(3.2)和(4.5)式知

综上,由$(4.15)$和$(4.16)$式知

下面考虑${\bf L}_0$的上界,推导过程和$(4.16)$式类似,由假设条件(A1)-(A4),积分规则的标准误差边界,系统$(2.1)$中的$x(0, t) = \int_0^A \beta(a, t, E(x)(a, t))x(a, t){\rm d}a$及$(4.3)$式知:存在一个$\hat{a},$当$1\le n\le N$时,有

最后一步用到了$A=Jh$.再由${\bf x}^0$和${\bf X}^0$的定义知: $\Vert{\bf x}^0-{\bf X}^0\Vert_{\infty}=0$.引理得证.

定义4.2^[7]   对$h\in H$,令$M_h>0$为一个由$h$确定的实数.如果存在两个正的常数$h_0$和$S$使得: $\forall h\in H$, $h\le h_0$,开球$B_{X_h}({\bf x}_h, M_h)$包含于${\bf \Gamma}_h$是定义域中,且对于开球中的任意两元${\bf V}_h, {\bf W}_h$,满足

则称离散化映射${\bf \Gamma}_h$关于${\bf x}_h$稳定.

引理4.3   若条件(A1)-(A4)成立,则离散化映射${\bf \Gamma}_h$关于阈值为$M_h$的${\bf x}_h$是稳定的.

证  令$\big({\bf V}^0, {\bf V}^1, \cdots, {\bf V}^N\big), \big({\bf W}^0, {\bf W}^1, \cdots, {\bf W}^N\big)\in B_{X_h}({\bf x}_h, M_h)$,并且设

当$0\le j\le J^*-1$时,将$P_{j+1}^{n+1}, R_{j+1}^{n+1}$分别带入$(4.4)$式可推得

同理,当$J^*\le j\le J-1$时,由$(4.5)$式得

当$0\le j\le J-1$时,由假设条件, $\Vert{\bf W}\Vert_{\infty}\le C$以及不等式$(4.12)$,由(4.19), (4.20)式可得

当$1\le j<n\le N$时,将$(4.21)$式由左至右递推可知

另一方面,当$1\le n<j$时,同样由$(4.21)$式递推可知

由$(4.3)$式可得

由不等式$(4.10)$及$\vert{\bf W}^n\Vert_{\infty}\le C$知

分别将(4.22), (4.23)和(4.25)式中的$|E_j^n|$乘以$h$并关于下标$j(0\le j\le J)$进行求和,对于$1\le n\le N$得

运用离散化的Gronwall引理得

最后将(4.26)式带入到(4.22), (4.23)和(4.25)式中,即得引理结论.

定义4.3^[7]   记全局离散误差为${\bf e}_h={\bf x}_h-{\bf X}_h.$如果存在$h_0>0$,使得$\forall h\in{\bf H}$且$h\le h_0$, $(4.8)$式有唯一的解${\bf X}_h$,且

那么称$\Gamma_h$收敛.

下面引用文献[23]中的已知结果:

引理4.4^[23]   假设$\Gamma_h$是一致的且关于阈值${\bf x}_h$是稳定的.如果$\Gamma_h$在$B({\bf x}_h, M_h)$上连续,且$h\rightarrow 0$时, $\Vert{\bf \Gamma}_h({\bf x}_h)\Vert_{Y_h}=o(M_h)$,那么下列结论成立:

(1)   $(4.8)$式在$B({\bf x}_h, M_h)$上有唯一的解;

(2)  上述解收敛并且$\Vert{\bf e}_h\Vert_{X_h}=O(\Vert{\bf \Gamma}_h({\bf x}_h)\Vert_{Y_h}).$

定理4.1   假设(A1)-(A4)成立.则当$h$足够小时,数值方法(3.3)-(3.5)有唯一的解${\bf X}_h\in B_{X_h}({\bf x}_h, Mh)$,并且有下式成立:

证   $\Gamma_h$的一致性和稳定性已分别由引理2.2和引理2.3给出,解的唯一性已由引理2.4给出,所以当步长$h\rightarrow 0$时,由方程(3.3)-(3.5)所得近似解收敛于系统的理论解.

例1  种群走向绝灭.选定参数: $A=10, \, T=10, \, \alpha = 0.6,$种群初始分布: $x_0(a)=4(10-a)^2;$

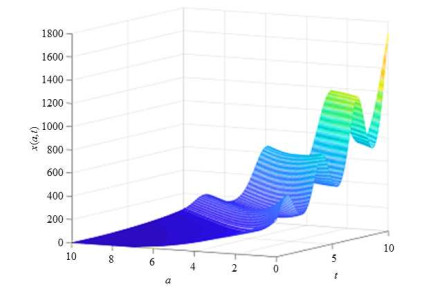
例2  种群持续生存.选定参数: $A=10, \; T=10, \; \alpha=0.5$种群初始分布: