1 引言
众所周知,许多经典的可积系统的初值问题可以由反散射方法来求解. 1997年, Fokas[1]借鉴反散射变换的思想提出了统一变换方法,我们称之为Fokas方法,该方法很好的求解了可积方程的初边值问题[2-5].就像全直线上的反散射方法一样, Fokas方法也是将初边值问题的解表示成相应的Riemann-Hilbert (RH)问题的解. 2012年, Lenells[6]首次将此方法做了推广,并且研究了Degasperis-Procesi方程在半直线上的初边值问题[7].在这之后,越来越多的学者开始关注可积系统的初边值问题[8-23].此外,基于RH方法得到的可积方程的多孤子解在近几年也得到了广泛研究[24-29].
2015年,张等[30]从耦合高阶Chen-Lee-Liu方程
出发,在约化条件
本文结构如下:在第二部分,给出了Lax对的谱分析.在第三部分,证明了HOCLL方程初边值问题的解可用RH问题的形式解唯一表示.
2 谱分析
HOCLL方程(1.2)有如下的Lax对[30]
其中
因此, Lax对方程(2.1)有下列形式
其中
因此,方程(2.3)等价为
写成全微分形式有
其中
其中,
然后,我们寻找方程(2.1)如下形式的一个解
将(2.8)式代入(2.5)式的
从得
由
这里
注意到方程(2.1)的守恒律
我们定义
其中
由于(2.12)式与积分路径无关,而且
因此, Lax对方程(2.5)可以写为
其中
由
因此,方程(2.14)可以写成
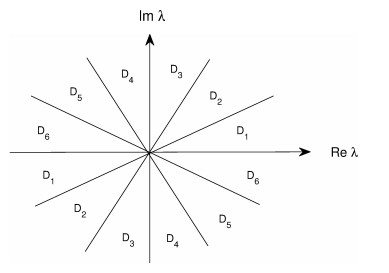
2.1 特征函数
假设
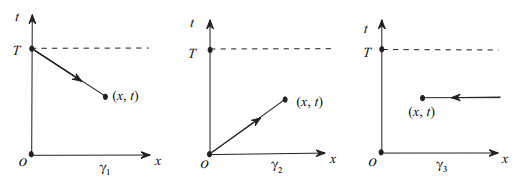
图 1
假设
同时,在曲线上有如下的不等式
为了得到
其中
图 2
2.2 谱函数和全局关系
为了导出RH问题的跳跃矩阵,定义两个
在方程(2.22)第一、二个式中分别取
由(2.22)和(2.23)式可以得到如下的全局关系
特别地,由于
其中
命题2.1 (对称性) 特征函数
有如下的对称性:
命题2.2 由方程(2.22)和(2.23)定义的谱函数
我们定义矩阵函数
利用方程(2.23)和(2.26),我们得到
2.3 跳跃矩阵及计算
为了研究方便,我们假设
矩阵函数
因此,我们有
命题2.3 假设
其中
其中
证 为了导出(2.31)式,我们把(2.22)和(2.27)式写成下面的形式
通过直接计算可以得到(2.33)式,并且
其中
2.4 留数条件
函数
命题2.4 记
(ⅰ)
(ⅱ)
(ⅲ)
(ⅳ)
证 这里我们只需证明(ⅰ),其余的留数计算与之类似.考虑
将
进一步地,我们有
这就是(ⅰ)式,证毕.
3 Riemann-Hilbert问题
在上一部分定义的
定理3.1 在方程(2.27)中,由
因此,
此外,
证 事实上,如果函数
定理3.2 (消灭定理)定理3.1中的带有边界条件
参考文献
A unified transform method for solving linear and certain nonlinear PDEs
Integrable nonlinear evolution equations on the half-line
The derivative nonlinear Schrödinger equation on the half-line
A Riemann-Hilbert approach to the Chen-Lee-Liu equation on the half line
A Riemann-Hilbert approach to the complex Sharma-Tasso-Olver equation on the half line
Initial-boundary value problems for integrable evolution equations with 3×3 Lax pairs
The Degasperis-Procesi equation on the half-line
The three wave equation on the half-line
A Riemann-Hilbert approach to the initial-boundary problem for derivative nonlinear Schrödinger equation
The Fokas-Lenells equation on the finite interval
A Riemann-Hilbert approach for the Novikov equation
The mixed coupled nonlinear Schrödinger equation on the half-line via the Fokas method
Initial-boundary value problems of the coupled modified Korteweg-de Vries equation on the half-line via the Fokas method
Initial-boundary value problems for the general coupled nonlinear Schrödinger equation on the interval via the Fokas method
An initial-boundary value problem for the integrable spin-1 Gross-Pitaevskii equations with a 4×4 Lax pair on the half-line
A Riemann-Hilbert approach to the complex Sharma-Tasso-Olver equation on the half Line
Initial-boundary value problems for the coupled higher-order nonlinear Schrödinger equations on the half-line
Riemann-Hilbert approach for an initial-boundary value problem of the two-component modified Korteweg-de Vries equation on the half-line
A Fokas approach to the coupled modified nonlinear Schrödinger equation on the half-line
Riemann-Hilbert approach for an initial-boundary value problem of an integrable coherently coupled nonlinear Schrödinger system on the half-line
The unified transform method to initial-boundary value problem of the coupled cubic-quintic nonlinear Schrödinger system
A Riemann-Hilbert approach to the initial-boundary value problem for Kundu-Eckhaus equation on the half line
广义Sasa-Satsuma方程在半直线上的初边值问题
An initial-boundary value problem for the generalized Sasa-Satsuma equation on the half-line
Riemann-Hilbert problems and N-soliton solutions for a coupled mKdV system
Riemann-Hilbert problems of a six-component fourth-order AKNS system and its soliton solutions
Application of the Riemann-Hilbert approach to the multicomponent AKNS integrable hierarchies
Riemann-Hilbert problems and soliton solutions of a multicomponent mKdV system and its reduction
Riemann-Hilbert problems of a six-component mKdV system and its soliton solutions
Riemann-Hilbert approach and N-soliton formula for a higher-order Chen-Lee-Liu equation
Rogue wave solutions of a higher-order Chen-Lee-Liu equation