Couette-Taylor流的力学机理与能量转换

Couette-Taylor流的力学机理与能量转换

王贺元^,¹^,²

Dynamical Mechanism and Energy Conversion of Couette-Taylor Flow

Wang Heyuan^,¹^,²

收稿日期: 2018-03-22

基金资助:

国家自然科学基金. 11572146
沈阳师范大学博士启动基金. 054-91900302009

Received: 2018-03-22

Fund supported:

国家自然科学基金. 11572146
沈阳师范大学博士启动基金. 054-91900302009

作者简介 About authors

王贺元,E-mail:987236994@qq.com , E-mail：987236994@qq.com

摘要

同轴圆筒间Couette-Taylor流问题是典型的旋转流动问题，它是层流到湍流过渡的范例，国内外众多学者对其进行了深入的研究.该文探讨Couette-Taylor流问题的力学机理与能量转换，通过将Couette-Taylor流三模混沌系统转换成Kolmogorov形系统，把系统的力矩分为四种类型：惯性力矩，内力矩，耗散力矩和外力矩.通过不同力矩的结合分析和研究了Couette-Taylor流产生混沌的关键因素和物理意义.研究了哈密顿能量，动能和势能之间的相互转换.讨论了能量与雷诺数之间的关系.研究表明四种力矩的耦合是产生混沌的必要条件，而且只有耗散力矩和驱动力矩（外力矩）相匹配时，系统才能产生混沌，其中任何三种力矩耦合均不可能产生混沌.圆筒旋转产生的外力矩供给系统能量，能量增长导致流动失稳，从而产生泰勒漩涡和混沌，进而得出了Couette-Taylor流的能量转换和物理意义.引进Casimir函数分析系统的动力学行为和能量转换，并估计混沌吸引子的界.Casimir函数反映了能量转换和轨道与平衡点间的距离，数值结果仿真出它们之间的关系.

关键词： Couette-Taylor流 ; 力学机理 ; Kolmogorov系统 ; 混沌

Abstract

There have been a lot of investigations which concern with rotating flow between two concentric cylinders (abbreviate frequently as Couette-Taylor Flow), Couette-Taylor flow is the typical rotation flow problems, It provides a paradigm from laminar to turbulent transition. Dynamical mechanism and energy conversion of Couette-Taylor flow are investigated in this paper, the Couette-Taylor flow chaotic system is transformed into Kolmogorov type system, which is decomposed into four types of torques:inertial torque, internal torque, dissipation and external torque. By the combinations of different torques, key factors of chaos generation and the physical meaning of Couette-Taylor Flow are studied. The conversion among Hamiltonian energy, kinetic energy and potential energy is investigated. The relationship between the energies and the Reynolds number is discussed. It concludes that the combination of the four torques is necessary conditions to produce chaos, and only when the dissipative torques matches the driving (external) torques can the system produce chaos, any combination of three types of torques cannot produce chaos. The external torque, which is provided by the rotation of the cylinder, supply the energy of the system, and that leads to Taylor vortex and chaos, the physical meaning and energy conversion of Couette-Taylor flow system are investigated. The Casimir function is introduced to analyze the system dynamics, and its derivation is chosen to formulate energy conversion. The bound of chaotic attractor is obtained by the Casimir function and Lagrange multiplier. The Casimir function reflects the energy conversion and the distance between the orbit and the equilibria. These relationships are illustrated by numerical simulations.

Keywords： Couette-Taylor flow ; Dynamical Mechanism ; Kolmogorov system ; Chaos

PDF (1761KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王贺元. Couette-Taylor流的力学机理与能量转换. 数学物理学报[J], 2020, 40(1): 243-256 doi:

Wang Heyuan. Dynamical Mechanism and Energy Conversion of Couette-Taylor Flow. Acta Mathematica Scientia[J], 2020, 40(1): 243-256 doi:

1 引言

同轴圆筒间旋转流动的Couette-Taylor流问题是近一个世纪以来人们普遍关注的热点问题,由于其流动形态的可观测性以及它在湍流研究中的基础性地位及其在流体机械、石油化工等领域的广泛应用,国际上将其列为非线性科学的范例之一.国内外众多学者对其复杂的动力学行为进行了大量深入的研究,相关文献非常丰富(文献[1-12]只是2000多篇文献中较少的一部分).如果内圆筒旋转,外圆筒静止,这种流动历经Couette流、Taylor涡流、Taylor行进波、波状螺旋漩涡、调制波状螺旋漩涡、湍状Taylor涡流等十几种波形最终进入湍流(见图 1),如果内外圆筒同时正向或反向旋转,可以观察到更为丰富的流动,具体见文献[3-12].

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1 Couette-Taylor流的演化

以往的研究工作大都侧重于从流动的稳定性和分岔理论开展研究,主要是利用分岔理论来解释和分析实验中观察到的流动发展到湍流前的各种涡流及其相互演化的过程,以及从层流过渡到湍流的方式及仿真等,而对流动的生成机理,能量转换及物理意义等问题很少有文献涉及.因此探讨Couette-Taylor流的生成机理和物理意义等相关问题是非常有意义和具有挑战性的.

混沌系统按其各项及相互作用是相当复杂的.如果从力学角度对混沌进行研究,可以从中发现更多的混沌基本成因.从力学角度研究混沌系统已经有了良好的开端,阿诺德^[13]用Kolmogorov系统来描述具有哈密顿函数的不同的强迫动力系统,流体动力系统等. Pasini和Pelino^[14]对Lorenz系统进行了研究,并给出了统一的柯尔莫哥洛夫(Kolmogorov)和洛伦茨(Lorenz)系统.齐和梁^[15]引进Casimir函数分析了Chen混沌系统的动力学行为和能量转换,揭示了能量转换和轨道与平衡点间的距离,并估计了混沌吸引子的界.文献[16]研究了Chen混沌系统力学机理与能量转换,将Chen混沌系统转换成Kolmogorov形系统,通过不同力矩的结合分析和研究了Chen混沌系统产生混沌的关键因素和物理意义.研究了哈密顿能量,动能和势能之间的相互转换.讨论了能量与雷诺数之间的关系.文献[17]研究了齐四翼混沌系统的力学机理与能量转换,通过与Kolmogorov系统和欧拉方程的比较,把四翼混沌系统的矢量场分解为惯性力矩、内力矩、耗散和外力矩来探讨产生混沌的基本因素.利用Lie-Poisson括号揭示哈密顿能,动能与势能的相互转换.通过五种情形分析研究了四翼混沌吸引子不同类型力矩的功能和作用以及产生不同类型动力学模式的关键因素.此外,借助扩展的Kolmogorov系统, Pelino等^[18]研究了洛伦兹系统的能量转换.上述几篇文献开启了从力学角度研究混沌系统的先河,但文献[15-17]中的混沌系统均为数值混沌系统(通过数值计算发现的混沌系统),没有明确的物理意义.借鉴这三篇文献的思想和方法我们探讨了具有明确物理意义的Couette-Taylor流问题,讨论的Couette-Taylor流三模混沌系统属于物理混沌系统(具有物理背景和物理意义的混沌系统),研究了Couette-Taylor流的动力机制,物理意义和能量转换.把Couette-Taylor流三模态系统(见文献[12])的状态变量视为角动量,将矢量场分解为惯性力矩,内转矩,耗散力矩和外力矩,不同的力矩的耦合视为不同的动力模式,通过分析各种力矩与Couette-Taylor流的不同模态的因果关系,揭示各种Taylor涡和混沌生成的力学机理.从力学角度分析同轴圆筒间旋转流动的各种涡流和混沌的生成机理目前还没有文献涉及.

由于Couette-Taylor流的全局吸引子是非常复杂和难于计算的. Couette-Taylor流系统的轨道从一个不稳定的平衡点移动到另一个不稳定的平衡点,相应地,轨道和平衡点之间的距离随参数和时间的不同而变化.我们发现,卡西米尔(Casimir)函数与距离有密切关系,关于洛伦茨吸引子的可预测性和能量可以通过能量转换来进行研究^[18].因此,通过引入卡西米尔函数的导数,我们给出了Couette-Taylor流系统的能量转换,并且分析了它们的动力学和能量转换.

本文的结构如下:第2节将Couette-Taylor系统转换为Kolmogorov系统.第3节分析了不同动力模式的力学机理.在第4节,引入卡西米尔函数来获得混沌吸引子的边界,探讨它的动态行为.第5节按扩展Kolmogorov系统和能量转换,分析了Couette-Taylor流系统的力学机制,势能和动能间的转换和卡西米尔函数的关系.最后,第6部分是总结.

2 Couette-Taylor流三模系统及其Kolmogorov系统

文献[2]利用同轴圆筒间隙区域Stokes算子的特征函数作为基函数对周期性边界条件Navier-Stokes方程进行傅里叶展开,将原偏微分方程组化为常微分方程组,取傅里叶级数的前三项,得到下列方程组

(2.1) $ \begin{equation} \left\{ \begin{array}{l} \dot x = - \sigma x + cy, \\ \dot y = -xz +arx -y, \\ \dot z = xy-bz , \end{array} \right. \end{equation} $

这里$ x, y, z $是傅里叶系数,它们是时间$ t $的函数, $ \sigma, a, b, c $都是正的参数, $ r $为雷诺数,与圆筒的旋转角速度成正比.当$ \sigma = 9.35, a = 0.758, b = 1.45, $$ c = 8.4 $系统存在混沌吸引子.为了发现系统(2.1)的状态变量的物理意义和系统(2.1)的力学机理我们引进如下三维形式的Kolmogorov系统

(2.2) $ \begin{equation} \dot X = \{X, H\} -\Lambda X+f, \end{equation} $

其中$ X = [x, y, z]^T $,反对称括号$ \{\cdot, \cdot\} $表示哈密顿函数$ H $动能部分的代数结构,以及cosymplectic矩阵$ J $,或Lie-Poisson结构^[19]

(2.3) $ \begin{equation} \{F, G\} = J_{ik}\partial_i F\partial_k G. \end{equation} $

系统(2.2)是Kolmogorov描述具有哈密顿函数的不同强迫动力系统,流体动力系统等引入的^[13].在欧拉方程中力(或力矩)$ \{X, H\} $是惯性力(离心力).系统(2.2)是具有耗散力和外力的广义欧拉方程^[19].经变量变换$ x\mapsto x, y\mapsto y, z\mapsto z-ar- c $,系统(2.1)化为

(2.4) $ \begin{equation} \left\{ \begin{array}{l} \dot x = - \sigma x + cy , \\ \dot y = -xz -cx -y, \\ \dot z = xy-bz-b(ar+c). \end{array} \right. \end{equation} $

变换之后系统(2.4)平衡点的数量和性质与原系统(2.1)的相同,但平衡点的位置发生了改变.容易获得系统(2.4)有如下三个平衡点:

$ O = [0, 0, -(ar+c)], \quad P^{\pm} = \bigg[\pm\sqrt{b(\frac{ac}{\sigma}r-1)}, \pm\sqrt{b\frac{\sigma}{c}(ar-\frac{\sigma}{c})}, -(c+\frac{\sigma}{c}) \bigg]. $

定义哈密顿能量(the Hamiltonian energy) $ H = K + U $,其中动能$ K = \frac{1}{2}(x^2+2y^2+2z^2) $,势能$ U = cz $.哈密顿能量$ H $包括动能(the kinetic energy)$ K $和势能(the potential energy)$ U $.则系统(2.4)被描述为如下的Kolmogorov系统

(2.5) $ \begin{equation} \dot X = \left( \begin{array}{c} cy \\ -xz -cx\\ xy\\ \end{array} \right ) -\left( \begin{array}{c} \sigma x \\ y\\ bz\\ \end{array} \right ) +\left( \begin{array}{c} 0 \\ 0\\ -b(ar+c)\\ \end{array} \right ) = \{X, H\} -\Lambda X+f, \end{equation} $

其中$ \Lambda = {\rm diag}(\sigma, 1, b) $, $ f = (0, 0, -b(ar+c))^T $.

注1 变量$ X $相当于角动量,时间导数$ \dot X $表示流体流动的反应力矩(the reaction torque).第一项$ \{X, H\} $是守恒项,包括由动能产生的惯性力矩和势能释放的内力矩.第二项$ \Lambda X $是耗散力矩,即摩擦或加热交换或粘滞力,最后一项$ f $是外力矩(驱动力矩).

3 系统(2.5)的动力学机制及其分析

本节我们研究不同类型的力矩对系统(2.5)的影响,从而发现产生Taylor涡和混沌的关键因素.

情形1 系统只包含惯性力矩(由动能$ K $产生的),即系统仅包含动能

(3.1) $ \begin{equation} \dot X = \{X, K\} = \left( \begin{array}{c} 0 \\ -xz\\ xy\\ \end{array} \right ). \end{equation} $

动能函数的导数$ \dot K = x\dot x+2y\dot y +2z\dot z = 0. $

显然,系统(3.1)是保守系统,因此,一个闭合的周期轨道产生如图 2(a)所示,状态变量$ z $的轨迹如图 2(b)所示.事实上,由于$ x $是常量,系统(3.1)是线性系统.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2 系统在惯性力矩下的动力学行为

情形2 系统包含哈密顿函数中的惯性力矩(由动能$ K $产生的)和内力矩(由势能$ U $释放的),即系统仅包含内能,相应的方程为

(3.2) $ \begin{equation} \dot X = \{X, H\} = \left( \begin{array}{c} cy \\ -xz-cx\\ xy\\ \end{array} \right ). \end{equation} $

哈密顿函数的导数$ \dot H = x\dot x+2y\dot y +2z\dot z+c\dot z = 0. $

系统(3.2)也是一个保守的系统,因此,如图 3(a)所示,产生一个闭合的周期轨道,状态$ z $的轨迹如图 3(b)所示.比较情形1和情形2,势能U的出现使解更频繁地振荡.由于$ c>0 $,系统是非线性系统,并且势能U的存在使产生的周期解频率比情形1大得多,这意味着内力矩使系统解移动的速度比情形1时快得多.频率取决于参数$ c $,内力矩(由U释放)加强了轨道的拉伸和收缩,这对Taylor涡和混沌的生成可能是潜在有效的.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3 系统在惯性力矩和内力矩下的动力学行为

情形3 系统包含惯性力矩,内力矩和耗散力矩,即系统包含内能和耗散因素,但不包含驱动因素,相应的方程为

(3.3) $ \begin{equation} \dot X = \{X, K+U\} -\Lambda X = \left( \begin{array}{c} cy \\ -xz -cx\\ xy\\ \end{array} \right ) -\left( \begin{array}{c} \sigma x \\ y\\ bz\\ \end{array} \right ), \end{equation} $

对于$ \sigma = 9.35, a = 0.758, b = 1.45, c = 8.4 $,容易获得

$ {\rm Div}(V) = \frac{\partial\dot x}{\partial x}+\frac{\partial\dot y}{\partial y} +\frac{\partial\dot z}{\partial z} = -\sigma-1-b<0, $

其中V是系统相空间的体积.因此,此情形下系统是耗散的,即相空间的体积在流量下以指数形式收缩^[20].哈密顿的能量变化率是

$ \dot H = x\dot x+2y\dot y +2z\dot z+c\dot z = -\sigma x^2-2y^2-2bz^2-bcz. $

不同于文献[14, 18]中讨论的Kolmogorov系统,我们不能通过哈密顿函数的导数来确定能量耗散. 图 4 (a)给出了哈密顿函数$ H $的时间演化,显示能量是耗散的,因为体积$ V $耗散从而能量减少,如图 4(b)所示.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4 能量函数的时间演化

情形4 系统在惯性力矩,内力矩和外力矩下,即系统包含内能和驱动因素,但不包含耗散因素,相应的方程为

(3.4) $ \begin{equation} \dot X = \{X, K+U\} +f = \left( \begin{array}{c} cy \\ -xz -cx\\ xy\\ \end{array} \right ) +\left( \begin{array}{c} 0 \\ 0\\ -b(ar+c)\\ \end{array} \right ), \end{equation} $

由于有了外力矩$ f $,总的角动量在外力矩的方向发展,这意味着轨道不仅在周期加倍内移动,而且还被外力矩拉伸以产生螺旋状的曲线,如图 5(a)$ (r = 27) $所示. 图 5(b)显示状态变量$ z $的振荡频率随时间增长($ r = 27 $).令$ V_1 = cz-x^2/2 $,那么它的导数$ \dot{V}_1 = -bc(ar+c)<0 $.导数积分后的,很容易获得$ V_1(t)-V_1(0) = \int^t_0(-bc(ar+c)){\rm d}s = -bc(ar+c)t $,即当$ t\rightarrow +\infty $或$ r\rightarrow +\infty $时, $ V_1(t)\rightarrow \infty $.也就是说$ x $或$ z $是无界的,因此,哈密顿函数H也趋于无穷,如图 6所示.实际上,外力矩主要增加了动能;相比之下,势能则受到外力矩的影响较小.可以看出,随着时间的推移,动能增加,这就导致了哈密顿能量的增加.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5 系统在惯性力矩，内力矩和外力矩下的动力学行为

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6 能量的演化

为了分析和比较各种力矩对实际Couettt-Taylor流动所起的作用,我们讨论了上面虚拟的四种情形,下面的情形5才具有真实的物理意义.

情形5 系统在全部力矩下,即系统包含内能,同时包含耗散因素和驱动因素,相应的方程为

(3.5) $ \begin{equation} \dot X = \{X, K\}+\{X, U\}-\Lambda X+f = \left( \begin{array}{c} cy \\ -xz -cx\\ xy\\ \end{array} \right ) -\left( \begin{array}{c} \sigma x \\ y\\ bz\\ \end{array} \right ) +\left( \begin{array}{c} 0 \\ 0\\ -b(ar+c)\\ \end{array} \right ). \end{equation} $

当$ r = 32 $时系统(3.5)存在混沌吸引子如图 7(a)所示.情形3中没有外力矩, Couette-Taylor流系统解趋于平衡点$ O $.而情形4下Couette-Taylor流系统解在没有耗散的情况下无限增长.因此,外力和耗散耦合是Couette-Taylor流系统产生混沌吸引子的必要条件.然而,当外力矩与耗散力矩不匹配时,耗散并不足以保证Couette-Taylor流系统的能量衰减,也就是说外力和耗散虽然是产生混沌的基本因素,但外力和耗散简单的耦合并不总是使系统产生混沌.例如,如图 7(b)所示. 图 8(a)绘制了当$ r = 76 $时系统的准周期吸引子.只有当参数$ r $在一定范围内取值($ 31.6\leq r\leq 315 $),且当驱动因素(外力)与耗散因素相匹配时,系统才可能产生混沌. 图 8(b)绘制动能和势能的时间演化($ r = 30 $),其中上曲线表示动能,下曲线表示势能,当动能接近波峰时,势能到达波谷,这说明这两种能量相互转化.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7 系统在全部力矩下的动力学行为

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8 系统（3.5）的动力学

4 系统(2.4)的卡西米尔(Casimir)函数及其全局稳定性分析

混沌系统具有一些奇异的性质:如初始灵敏性和解的有界性.对于非混沌系统,正Lyapunov指数意味着系统解无限制地增长.然而,对于一个有界的混沌吸引子来说,其轨线增长的同时在不断的折叠,因此,解的边界性质在混沌系统研究中是至关重要的.通常很难找到混沌吸引子的边界,利用拉格朗日乘数法和卡西米尔函数法,我们得到了Couette-Taylor流系统混沌吸引子的边界.数值模拟表明,这是一个清晰的边界.卡西米尔函数$ C $,就像在流体动力学中的涡量拟能(enstrophy)或势能涡度,对于分析一个动态系统的稳定性条件和全局描述非常有用,它由括号(2.3)的内核定义,即

$ \{C, G\} = 0, \quad \forall G\in C^\infty(g^*), $

这意味着在Lie-Poisson括号下卡西米尔函数与每个函数可交换^[19].对于Couette-Taylor流系统来说,卡西米尔函数定义为

$ C = \frac{1}{2}(x^2+y^2+z^2). $

由(2.3)式和文献[19],我们有

$ \{C, G\} = -X\cdot(\nabla C \times \nabla G) = -X\cdot(X \times \nabla G) = 0, $

其中$ X = [x, y, z]^T $.根据方程(2.4)得

$ \dot{C} = -(\sigma x^2+y^2+bz^2+b(ar+c)z). $

令

$ \Xi_0 = \bigg\{(x, y, z)\mid \sigma x^2+y^2+b(z+(ar+c))^2 = \frac{(ar+c)^2}{4}\bigg\}. $

显然$ \Xi_0 $是$ {\Bbb R}^3 $中的椭球,在$ \Xi_0 $表面上$ \dot{C} = 0 $,所以$ C(t) $的所有极值点均位于$ \Xi_0 $的表面.当系统(2.5)或(5.2)的轨线从$ \Xi_0 $的内部移出时$ \dot{C}<0 $,因此卡西米尔函数下降到$ \dot{C} = 0 $,达到其极小值.当轨线进入$ \Xi_0 $内,有$ \dot{C}>0 $,然后,卡西米尔函数增加直到$ \dot{C} = 0 $达到它的最大值.应该注意的是,三个平衡点均位于$ \Xi_0 $的表面,因为平衡点是通过$ \dot{X} = 0 $求得的,推得$ \dot{C} = 0 $.受文献[22]方法的启发,下面我们给出卡西米尔函数和混沌吸引子的边界.

定理4.1 卡西米尔函数被限制在如下集合内

$ \Xi = \{(x, y, z) |x^2+y^2+z^2\leq(ar+c)^2\}. $

证根据上述分析, $ C(t) $的最大最小值点均位于集合$ \Xi_0 $内,因此, $ C(t) $的上界可以用如下有约束的优化问题来处理

(4.1) $ \begin{equation} \begin{array}{lll} \max \quad C = \frac{1}{2}(x^2+y^2+z^2), \\ {\rm s.t.}\quad \sigma x^2+y^2+bz^2+b(ar+c)z = 0.\\ \end{array} \end{equation} $

定义拉格朗日函数

$ L = \frac{1}{2}(x^2+y^2+z^2)+\lambda(\sigma x^2+y^2+bz^2+b(ar+c)z), $

其中$ \lambda $是拉格朗日乘子.

通过计算我们得到如下关于变量的导数

(4.2) $ \begin{equation} \left\{ \begin{array}{lll} \frac{\partial L}{\partial x} = x+2\lambda \sigma x = 0, \\ \frac{\partial L}{\partial y} = y+2\lambda y = 0, \\ \frac{\partial L}{\partial z} = z+2b\lambda z+b\lambda (ar+c) = 0, \\ \frac{\partial L}{\partial \lambda} = \sigma x^2+y^2+bz^2+b(ar+c)z = 0, \end{array} \right. \end{equation} $

因此得到两个解

$ (x, y, z, \lambda) = (0, 0, 0, 0) \quad \mbox{和}\quad (0, 0, -(ar+c), -\frac{1}{b}). $

所以, $ C $的最大值为$ (ar+c)^2/2 $,即

$ C = \frac{1}{2}(x^2+y^2+z^2)\leq \frac{1}{2}(ar+c)^2. $

证毕.

定理4.1给出了Couette-Taylor流系统混沌吸引子边界的精确估计.卡西米尔函数的值如图 9(a) ($ r = 40 $)所示,我们可以看到函数$ C(t) $以$ (ar+c)^2/2 $为上界振荡.混沌吸引子被包围在边界球内,如图 9(b)所示.为了显示卡西米尔函数与平衡点$ P^\pm $之间的关系,我们定义两种距离:

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9 </b></p> </div> </div> <br> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(4.3)</label><tex-math id="E4.3"> $ \begin{equation} D_1(t) = |X(t)-P^+|, \quad D_2(t) = |X(t)-P^-|, \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C47">这表示系统(2.5)的轨道与平衡点<span class="formulaText"><inline-formula><tex-math id="M95">$ P^\pm $</tex-math></inline-formula></span>之间的距离.在<a class="table-icon" style="color:#2150f9" href="#Fig10"; id="inline_content图 10(a)">图 10(a)</a> (<span class="formulaText"><inline-formula><tex-math id="M96">$ r = 30 $</tex-math></inline-formula></span><span class="formulaNumber">)</span>中,实线是Casimir函数,虚线是<span class="formulaText"><inline-formula><tex-math id="M97">$ D_1(t) $</tex-math></inline-formula></span>和<span class="formulaText"><inline-formula><tex-math id="M98">$ D_2(t) $</tex-math></inline-formula></span><span class="formulaNumber">.</span>为了突出他们间的关系,距离的振幅放大了. <a class="table-icon" style="color:#2150f9" href="#Fig10"; id="inline_content图 10(a)">图 10(a)</a>表明,当轨线远离平衡点<span class="formulaText"><inline-formula><tex-math id="M99">$ P^+ $</tex-math></inline-formula></span>或<span class="formulaText"><inline-formula><tex-math id="M100">$ P^- $</tex-math></inline-formula></span>时卡西米尔函数达到最大值.当轨线同时接近平衡点<span class="formulaText"><inline-formula><tex-math id="M101">$ P^\pm $</tex-math></inline-formula></span>时,卡西米尔函数达到最小值. <a class="table-icon" style="color:#2150f9" href="#Fig10"; id="inline_content图 10(b)">图 10(b)</a> (<span class="formulaText"><inline-formula><tex-math id="M102">$ r = 31 $</tex-math></inline-formula></span><span class="formulaNumber">)</span>中显示了更紧密的关系,在这个图中,虚线是<span class="formulaText"><inline-formula><tex-math id="M103">$ D_1(t) $</tex-math></inline-formula></span>与<span class="formulaText"><inline-formula><tex-math id="M104">$ D_2(t) $</tex-math></inline-formula></span>之和,它与Casimir函数具有类似的动态.他们的极值点几乎在同一时间点,而且他们也有同样的上升和下降趋势.</p> </div> </div> <h3 style="position: absolute; opacity: 0; filter:Alpha(opacity=0);">图 10</h3> <div class="content-zw-img" id="Fig10"> <div class="content-zw-img-img figure outline_anchor" onmouseleave="likai(this);"> <img src="sxwlxb-40-1-243-10.jpg" onclick="clickss(this)" onmouseover="huoqukuanduimg(this);" class="tupian"> <p class="tishi"> <a href="sxwlxb-40-1-243-10.jpg.html" target="_blank">新窗口打开</a>| <a href="sxwlxb-40-1-243-10.jpg.zip">下载原图ZIP</a>| <a href="sxwlxb-40-1-243-10.jpg.ppt">生成PPT</a> </p> </div> <div class="content-zw-img-shuoming"> <p class="content-zw-img-shuoming-title-cn"><b>图 10 <strong>函数与距离<i>D</i><sub>1</sub>，<i>D</i><sub>2</sub>的关系</strong><br> </b></p> </div> </div> <br> <div class="paragraph"> <div class="content-zw-1"> <p id="C48">当圆筒的角速度<span class="formulaText"><inline-formula><tex-math id="M105">$ \omega $</tex-math></inline-formula></span>增大(<span class="formulaText"><inline-formula><tex-math id="M106">$ r $</tex-math></inline-formula></span>增大)时,系统(2.4)的动能增加,如<a class="table-icon" style="color:#2150f9" href="#Fig11"; id="inline_content图 11">图 11</a>所示,外力矩主要是增加动能,最终导致流动失稳而出现泰勒涡和混沌. <a class="table-icon" style="color:#2150f9" href="#Fig11"; id="inline_content图 11">图 11</a>显示了距离<span class="formulaText"><inline-formula><tex-math id="M107">$ D_1 $</tex-math></inline-formula></span>和<span class="formulaText"><inline-formula><tex-math id="M108">$ D_2 $</tex-math></inline-formula></span>的总和与卡西米尔函数随参数<span class="formulaText"><inline-formula><tex-math id="M109">$ r $</tex-math></inline-formula></span>变化的变化趋势.</p> </div> </div> <h3 style="position: absolute; opacity: 0; filter:Alpha(opacity=0);">图 11</h3> <div class="content-zw-img" id="Fig11"> <div class="content-zw-img-img figure outline_anchor" onmouseleave="likai(this);"> <img src="sxwlxb-40-1-243-11.jpg" onclick="clickss(this)" onmouseover="huoqukuanduimg(this);" class="tupian"> <p class="tishi"> <a href="sxwlxb-40-1-243-11.jpg.html" target="_blank">新窗口打开</a>| <a href="sxwlxb-40-1-243-11.jpg.zip">下载原图ZIP</a>| <a href="sxwlxb-40-1-243-11.jpg.ppt">生成PPT</a> </p> </div> <div class="content-zw-img-shuoming"> <p class="content-zw-img-shuoming-title-cn"><b>图 11 <strong>能量和Casimir函数相对于<i>r</i>的演化</strong><br> </b></p> </div> </div> <br> <div class="paragraph"> <div class="content-zw-1"> <p id="C49">根据以上理论分析和仿真结果,我们得出如下结论,当<span class="formulaText"><inline-formula><tex-math id="M110">$ acr<\sigma $</tex-math></inline-formula></span>时,系统(2.4)仅存在平衡点<span class="formulaText"><inline-formula><tex-math id="M111">$ O $</tex-math></inline-formula></span>,这种定常的状态表明流体处于静止状态, Couette-Taylor流处于层流的状态,即流体围绕中心轴旋转,即Couette流动.当<span class="formulaText"><inline-formula><tex-math id="M112">$ acr>\sigma $</tex-math></inline-formula></span>,系统存在以下三个平衡: <span class="formulaText"><inline-formula><tex-math id="M113">$ O, P^+, P^-, $</tex-math></inline-formula></span>平衡点<span class="formulaText"><inline-formula><tex-math id="M114">$ O $</tex-math></inline-formula></span>从稳定结点变成鞍结点,新平衡点<span class="formulaText"><inline-formula><tex-math id="M115">$ P^{\pm} $</tex-math></inline-formula></span>是稳定的,这种稳定的状态代表稳定的泰勒涡,如<a class="table-icon" style="color:#2150f9" href="#Fig1"; id="inline_content图 1(a)">图 1(a)</a>.新的平衡点随着<span class="formulaText"><inline-formula><tex-math id="M116">$ r $</tex-math></inline-formula></span>增加逐渐丧失其稳定性,他们从稳定结点发展到稳定焦点,最后变成了鞍结点.同时,系统(2.4)的轨线趋于<span class="formulaText"><inline-formula><tex-math id="M117">$ P^{\pm} $</tex-math></inline-formula></span>,在<span class="formulaText"><inline-formula><tex-math id="M118">$ P^{+} $</tex-math></inline-formula></span>和<span class="formulaText"><inline-formula><tex-math id="M119">$ P^{-} $</tex-math></inline-formula></span>之间来回跳跃,对应的实际流动如<a class="table-icon" style="color:#2150f9" href="#Fig1"; id="inline_content图 1(b)">图 1(b)</a>, <a class="table-icon" style="color:#2150f9" href="#Fig1"; id="inline_content(c)">(c)</a>, <a class="table-icon" style="color:#2150f9" href="#Fig1"; id="inline_content(d)">(d)</a>所示.距离<span class="formulaText"><inline-formula><tex-math id="M120">$ D_1 $</tex-math></inline-formula></span>与<span class="formulaText"><inline-formula><tex-math id="M121">$ D_2 $</tex-math></inline-formula></span>之和随<span class="formulaText"><inline-formula><tex-math id="M122">$ r $</tex-math></inline-formula></span>增大而单调递增.动能从最小值逐渐增加, Casimir函数也有类似的增加趋势.随着泰勒涡的稳定性的丧失(<a class="table-icon" style="color:#2150f9" href="#Fig1"; id="inline_content图 1(a)">图 1(a)</a>)泰勒行进波,旋转波和调制波状泰勒涡相继出现(<a class="table-icon" style="color:#2150f9" href="#Fig1"; id="inline_content图 1(b)">图 1(b)</a>, <a class="table-icon" style="color:#2150f9" href="#Fig1"; id="inline_content(c)">(c)</a>, <a class="table-icon" style="color:#2150f9" href="#Fig1"; id="inline_content(d)">(d)</a>),在耗散和驱动的内禀作用下,系统的内能不断增大,从各种规则涡流经由暂态混沌最终到达混沌.在<a class="table-icon" style="color:#2150f9" href="#T1"; id="inline_content表 1">表 1</a>中,我们给出了这些相关结论的细节.</p> </div> </div> <div class="zw-zsbg figure_table outline_anchor"> <div class="table_anchor" style="display: none; "><b></b></div> <div class="caption_title" style="display: none; "><b>表 1</b></div> <div class="shitibiao"> <p class="content-zw-biao-title-cn"> <strong>表 1</strong> <span><i>σ</i>=9.35,<i>a</i>=0.758,<i>b</i>=1.45,<i>c</i>=8.4,<i>r</i>取不同值时三模系统(2.1)的动力学行为与能量演化及其相应的Couette-Taylor流实际运动</span> </p> </div> <div class="table-responsive" id="T1" style="width: 700px;margin: 0 auto;"> <table width="91%" class="tablea table"><thead><tr><td align="center"><i>r</i>值范围</td><td align="center">0<<i>acr</i><<i>σ</i>0 <i>r</i><sub>1</sub>=1.4685</td><td align="center" colspan="4"><i>acr</i>><i>σ</i><br/><i>r</i><sub>e</sub>=1.7532 <i>r<sub>g</sub></i>=27.5452 <i>r<sub>h</sub></i>=31.6102</td></tr></thead><tbody><tr><td align="center">定点<i>O</i></td><td align="center">稳定结点</td><td align="center" colspan="4">鞍结点(一个方向不稳,另两个方向稳定)</td></tr><tr><td align="center">定点<i>P</i><sup>+</sup>和<i>P</i><sup>-</sup></td><td align="center">不存在</td><td align="center">稳定结点</td><td align="center">稳定结点</td><td align="center">稳定结点</td><td align="center">鞍点</td></tr><tr><td align="center">系统(2.4)相空间中的运动情况</td><td align="center">趋于稳定定态<i>O</i></td><td align="center">趋于稳定定态<i>P</i><sup>+</sup>或<i>P</i><sup>-</sup></td><td align="center">运动最终按螺旋线趋于<i>P</i><sup>+</sup>或<i>P</i><sup>-</sup></td><td align="center">同左,但越靠近<i>r<sub>h</sub></i>，轨线在<i>P</i><sup>+</sup>和<i>P</i><sup>-</sup>之间来回跳动的越频繁,出现暂态混沌,最终趋于<i>P</i><sup>+</sup>或<i>P</i><sup>-</sup></td><td align="center">不稳定极限环(亚临界霍普夫分岔)</td></tr><tr><td align="center">动能</td><td align="center">最小值</td><td align="center" colspan="2">逐渐增大</td><td align="center">保持增大</td><td align="center">增长</td></tr><tr><td align="center">Casimir函数</td><td align="center">最小值</td><td align="center" colspan="2">逐渐增大</td><td align="center">保持增大</td><td align="center">增长</td></tr><tr><td align="center"><i>D</i><sub>1</sub>与<i>D</i><sub>2</sub>之和</td><td align="center">不存在</td><td align="center" colspan="2">逐渐递增</td><td align="center">递增</td><td align="center">逐渐增大</td></tr><tr><td align="center">Coutte-Talor流的实际流动</td><td align="center">Couette流</td><td align="center" colspan="2">形成规则的Talor涡流及Talor行进波等如图 1(a)(b)(c)</td><td align="center">经过波状涡流等达到暂态混沌如图 1(d)</td><td align="center">不规则湍流(混沌)如图 1(d)</td></tr></tbody></table> </div> <p class="biaotishi1"> <a href="sxwlxb-40-1-243/T1.html" target="_blank">新窗口打开</a>| <a href="sxwlxb-40-1-243/T1.csv.zip">下载CSV</a> </p> </div> <br> <h2 class="title-biaoti outline_anchor" level="1" id="outline_anchor_1"> 5 能量转换 </h2> <div class="paragraph"> <div class="content-zw-1"> <p id="C50">我们注意到系统(2.5)的第一项是由哈密顿能量传递的力矩,它似乎与后面两项,即耗散和外力矩没有关系,但从<a class="table-icon" style="color:#2150f9" href="#Fig11"; id="inline_content图 11">图 11</a>中我们发现能量与这两项有关.由于每一类型的力矩是一个耦合的线性或非线性的具有三个分量的矢量,其作用于一个质点上,因此很难研究系统(2.5)的力矩.但是,由于能量是一个标量,所以通过研究能量来发现力矩特征是很容易的,而能量是流体流动的一个重要因素,在接下来的讨论中,我们讨论了能量与这两种力矩的关系.莫里森<sup>[<a class="demo-basic" href="javascript:;" onmouseover="jjaxxawwhah(this,'b21')">21</a>]</sup>通过Lyapunov函数将哈密顿动力学的Li-Poisson括号扩展为包括耗散,即</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(5.1)</label><tex-math id="E5.1"> $ \begin{equation} \dot X = \{X, H\} +\langle X, L\rangle, \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C51">其中<span class="formulaText"><inline-formula><tex-math id="M124">$ \langle F, L\rangle = g_{ij}\frac{\partial F}{\partial x_i}\frac{\partial L}{\partial x_j} $</tex-math></inline-formula></span>是爱因斯坦符号, <span class="formulaText"><inline-formula><tex-math id="M125">$ L $</tex-math></inline-formula></span>是一个Lyanpunov函数耗散部分, <span class="formulaText"><inline-formula><tex-math id="M126">$ g_{ij} = \frac{1}{2}\varepsilon_{im}^n \varepsilon_{kn}^m $</tex-math></inline-formula></span>是Cartan-Killing指标.运用哈密顿能量与耗散能量交换思想,佩利诺等<sup>[<a class="demo-basic" href="javascript:;" onmouseover="jjaxxawwhah(this,'b22')">22</a>]</sup>用<span class="formulaText"><inline-formula><tex-math id="M128">$ L+G $</tex-math></inline-formula></span>替换<span class="formulaText"><inline-formula><tex-math id="M129">$ L $</tex-math></inline-formula></span>,其中<span class="formulaText"><inline-formula><tex-math id="M130">$ G $</tex-math></inline-formula></span>是外力释放的能量.因此,方程(2.5)重写为</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(5.2)</label><tex-math id="E5.2"> $ \begin{equation} \dot X = \{X, H\} +\langle X, L\rangle+\langle X, G\rangle, \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C52">其中<span class="formulaText"><inline-formula><tex-math id="M131">$ L = \frac{1}{2}(\sigma x^2+y^2+bz^2), G = b(ar+c)z $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M132">$ \langle X, P\rangle = -\frac{\partial P}{\partial X} $</tex-math></inline-formula></span><span class="formulaNumber">.</span>方程(5.2)可以解释为整个混沌系统包含四种类型的能量:动能、势能、耗散能和外力能,这些能量转换为四种类型的力矩:惯性力矩、内力矩、耗散力矩和外力矩.对于Couette-Taylor流,流体粒子包含动能和源自于重力、热量损失以及辐射吸收的势能,作用于流体粒子上的总力矩产生角加速度.</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C53">根据方程(2.3)和(5.2),我们有</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(5.3)</label><tex-math id="E5.3"> $ \begin{equation} \frac{\partial K}{\partial X}\{X, H\} = \{K, H\} , \quad \quad\frac{\partial K}{\partial X}\langle X, L\rangle = \langle K, L\rangle. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C54">那么</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(5.4)</label><tex-math id="E5.4"> $ \begin{eqnarray} \dot K& = &\frac{\partial K}{\partial X}\dot{X} = \frac{\partial K}{\partial X}(\{X, H\}+\langle X, L\rangle+\langle X, G\rangle)\\ & = & \{K, H\} +\langle K, L\rangle+\langle K, G\rangle\\ & = &\{K, U\} +\langle K, L\rangle+\langle K, G\rangle\\ & = & -cxy-[\sigma x^2+2y^2+2bz^2+2b(ar+c)z], \end{eqnarray} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C55">其中<span class="formulaText"><inline-formula><tex-math id="M133">$ \{K, U\} = -cxy $</tex-math></inline-formula></span><span class="formulaNumber">.</span>因此,动能的变化率与势能、耗散能、外能量有一定的关系.同理,我们也有</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(5.5)</label><tex-math id="E5.5"> $ \begin{equation} \dot{U} = \{U, K\}+\langle U, L\rangle+\langle U, G\rangle = cxy-bcz-bc(ar+c), \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C56">这意味着势能的变化率等于它与动能、耗散能量和外部能量的交换.</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C57">由于<span class="formulaText"><inline-formula><tex-math id="M134">$ \{C, K\} $</tex-math></inline-formula></span>和<span class="formulaText"><inline-formula><tex-math id="M135">$ \{C, U\} $</tex-math></inline-formula></span>都为零,卡西米尔函数显然不会与<span class="formulaText"><inline-formula><tex-math id="M136">$ U $</tex-math></inline-formula></span>和<span class="formulaText"><inline-formula><tex-math id="M137">$ K $</tex-math></inline-formula></span>交互(interact with).因此,引入新状态函数<sup>[<a class="demo-basic" href="javascript:;" onmouseover="jjaxxawwhah(this,'b22')">22</a>]</sup>. <span class="formulaText"><inline-formula><tex-math id="M139">$ W = \dot{C} = -(2L+G) $</tex-math></inline-formula></span><span class="formulaNumber">.</span>卡西米尔函数是热力学能,因此,卡西米尔变化率为耗散与供给能量之间的交换率.通过类似的方法我们有</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(5.6)</label><tex-math id="E5.6"> $ \begin{eqnarray} \dot W& = &\{W, K\} +\{W, U\} +\langle W, L\rangle+\langle W, G\rangle\\ & = &-[2\sigma c-2c+2(b-1)z+b(ar+c)]xy\\ &&+2\sigma^2x^2+2y^2+2b^2z^2+3b^2(ar+c)z+b^2(ar+c)^2. \end{eqnarray} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C58">然后, Couette-Taylor流系统的能量转换可以写成</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(5.7)</label><tex-math id="E5.7"> $ \begin{equation} \left\{ \begin{array}{lll} \dot K = -\{U, K\}+\langle K, L+G\rangle, \\ \dot{U} = \{U, K\}+\langle U, L+G\rangle, \\ \dot W = \{W, K\} +\{W, U\} +\langle W, L\rangle+\langle W, G\rangle\\ \quad\ = -[2\sigma c-2c+2(b-1)z+b(ar+c)]xy\\ \qquad\ + 2\sigma^2x^2+2y^2+2b^2z^2+3b^2(ar+c)z+b^2(ar+c)^2, \end{array} \right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C59">这考虑了在<span class="formulaText"><inline-formula><tex-math id="M140">$ K, U $</tex-math></inline-formula></span>和<span class="formulaText"><inline-formula><tex-math id="M141">$ W $</tex-math></inline-formula></span>交换项中的耗散和力.方程(5.4)–(5.7)表明参数<span class="formulaText"><inline-formula><tex-math id="M142">$ r $</tex-math></inline-formula></span>对Couette-Taylor流系统的能量演化有显著影响.</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C60">在上面的公式中,当<span class="formulaText"><inline-formula><tex-math id="M143">$ xy<0 $</tex-math></inline-formula></span>时, <span class="formulaText"><inline-formula><tex-math id="M144">$ \{K, U\} $</tex-math></inline-formula></span>是正数;因此,有势能转变为动能的净转换.相应的,当<span class="formulaText"><inline-formula><tex-math id="M145">$ xy>0 $</tex-math></inline-formula></span>时, <span class="formulaText"><inline-formula><tex-math id="M146">$ \{K, U\} $</tex-math></inline-formula></span>为负数,有动能变为势能的净转换.</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C61">Couette-Taylor流系统有螺旋式轨道,它的轨道从一个不稳定的平衡点移动到另一个不稳定的平衡点.当轨道远离不稳定的平衡点之一时, <span class="formulaText"><inline-formula><tex-math id="M147">$ D_1 $</tex-math></inline-formula></span>与<span class="formulaText"><inline-formula><tex-math id="M148">$ D_2 $</tex-math></inline-formula></span>的距离和因参数<span class="formulaText"><inline-formula><tex-math id="M149">$ r $</tex-math></inline-formula></span>增大而逐渐增大,如<a class="table-icon" style="color:#2150f9" href="#Fig12"; id="inline_content图 12">图 12</a>所示.也就是<span class="formulaText"><inline-formula><tex-math id="M150">$ r $</tex-math></inline-formula></span>增大,使得驱动与耗散相匹配,二者共同作用导致系统内能增大,生成各种泰勒涡最终出现混沌.因而轨线在两个不稳定的平衡点之间频繁跳跃,使得<span class="formulaText"><inline-formula><tex-math id="M151">$ D_1 $</tex-math></inline-formula></span>与<span class="formulaText"><inline-formula><tex-math id="M152">$ D_2 $</tex-math></inline-formula></span>的距离和也逐渐增大.</p> </div> </div> <h3 style="position: absolute; opacity: 0; filter:Alpha(opacity=0);">图 12</h3> <div class="content-zw-img" id="Fig12"> <div class="content-zw-img-img figure outline_anchor" onmouseleave="likai(this);"> <img src="sxwlxb-40-1-243-12.jpg" onclick="clickss(this)" onmouseover="huoqukuanduimg(this);" class="tupian"> <p class="tishi"> <a href="sxwlxb-40-1-243-12.jpg.html" target="_blank">新窗口打开</a>| <a href="sxwlxb-40-1-243-12.jpg.zip">下载原图ZIP</a>| <a href="sxwlxb-40-1-243-12.jpg.ppt">生成PPT</a> </p> </div> <div class="content-zw-img-shuoming"> <p class="content-zw-img-shuoming-title-cn"><b>图 12 <strong><i>D</i><sub>1</sub>与<i>D</i><sub>2</sub>的距离和与Casimir函数关于<i>r</i>的演化</strong><br> </b></p> </div> </div> <br> <div class="paragraph"> <div class="content-zw-1"> <p id="C62">虽然Couette-Taylor流混沌系统与Lorenz系统不同,但能量转换时间演化与文献[<a class="demo-basic" href="javascript:;" onmouseover="jjaxxawwhah(this,'b18')">18</a>]的结果相似,能量、西米尔函数以及<span class="formulaText"><inline-formula><tex-math id="M153">$ D_1 $</tex-math></inline-formula></span>与<span class="formulaText"><inline-formula><tex-math id="M154">$ D_2 $</tex-math></inline-formula></span>的距离之和与外力矩(雷诺数<span class="formulaText"><inline-formula><tex-math id="M155">$ r $</tex-math></inline-formula></span><span class="formulaNumber">)</span>间的演化关系是本文的重要发现.</p> </div> </div> <h2 class="title-biaoti outline_anchor" level="1" id="outline_anchor_1"> 6 结论 </h2> <div class="paragraph"> <div class="content-zw-1"> <p id="C63">本文研究了Couette-Taylor流类洛伦兹系统的动力学机理和能量转换,通过理论和数值结果揭示了Couette-Taylor流问题的力学机制和物理意义.首先,探讨了Couette-Taylor流类洛伦兹系统作为柯尔莫哥洛夫系统的力学和物理意义.剖析了Couette-Taylor流混沌系统四种不同类型的力矩,研究了这些力矩的耦合的五种情况,探讨了产生泰勒涡和混沌的关键因素.在保守的情况下,哈密顿量是一个常数,相应的方程产生周期解.当耗散力矩或外力矩加入到保守系统中时,哈密顿函数趋近于零或无穷大,对应的系统不会产生混沌.当考虑到所有力矩时, Couette-Taylor流系统才产生混沌,并且动能和势能之间相互转换.对于Couette-Taylor流系统,内能、耗散因素和驱动因素并存是产生混沌的必要条件,而且,只有当耗散与驱动相匹配时,系统才能生成混沌.圆筒旋转的机械能为系统提供能量,增加的动能导致流动不稳定,依次生成Talor涡流、Talor行进波和波状涡流等经过暂态混沌,最终到达混沌.其次,本文将Couette-Taylor流混沌系统作为一个扩展的Kolmogorov系统研究了其力学和物理意义.引进卡西米尔函数来分析系统动力学和能量转换.两种不稳定平衡点的距离之和与卡西米尔函数有密切的关系,它们的时间演化是一致的.卡西米尔函数是内能,因此,它的变化速率是耗散与供给能量(外力矩)之间的交换速率.内能的导数起着能量转换的作用,平衡点距离的时间演化也有类似的动态.</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <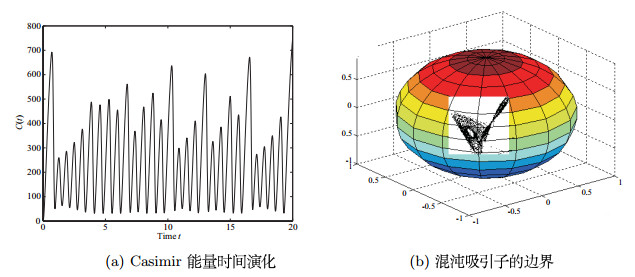p id="C64">Couette-Taylor流系统是耗散系统,其有界性是不平凡的,通过拉格朗日乘数法和卡西密尔函数法,得到了混沌吸引子的一个清晰的边界,数值仿真显示了方法的有效性.</p> </div> </div> <div class="cankaowenxian1"></div> <h2 class="title-biaoti"> <span class="outline_anchor" level="1">参考文献 </span> <div class="btn-group"> <button style="font-size:11px;padding:3px;" type="button" onclick="sddas();" class="btn btn-info dropdown-toggle" data-toggle="dropdown"> View Option <span class="caret"></span> </button> <ul class="dropdown-menu kkaqqqq" role="menu" style="background:#e1e7ea;padding-left:0px !important;"> <li onclick="daxcbdh();"><a href="javascript:;" class="ref_sort" type="1" style="color:#000;">原文顺序</a></li> <li onclick="daxcbdh();"><a href="javascript:;" class="ref_sort" type="2" style="color:#000;">文献年度倒序</a></li> <li onclick="daxcbdh();"><a href="javascript:;" class="ref_sort" type="3" style="color:#000;">文中引用次数倒序</a></li> <li onclick="daxcbdh();"><a href="javascript:;" class="ref_sort" type="4" style="color:#000;">被引期刊影响因子</a></li> </ul> </div> </h2> <div class="cankaowenxian"> <div id="b1" name="b1" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [1] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Chen</surname> <given-names>F</given-names> </name>, <name> <surname>Hsien</surname> <given-names>D Y</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">A model study of stability of couette flow</p><source>Comm on Appl Math and Comput</source>, <year>1987</year>, <volume><strong>1</strong></volume> (<issue>2</issue>): <fpage>22</fpage>- <lpage>33</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_physics%2f0303009" target="_blank">URL</a> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8221"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b1')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b2" name="b2" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [2] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Wang</surname> <given-names>H Y</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Lorenz systems for the incompressible flow between two concentric rotating cylinders</p><source>Journal of Partial Differential Equations</source>, <year>2010</year>, <volume><strong>23</strong></volume> (<issue>3</issue>): <fpage>209</fpage>- <lpage>221</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="doi"> DOI:<a href="https://doi.org/10.4208/jpde.v23.n3.1" target="_blank">10.4208/jpde.v23.n3.1</a> </span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8222"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b2')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b3" name="b3" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [3] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Wang</surname> <given-names>H Y</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">The chaos behavior and simulation of three model systems of Couette-Taylor flow</p><source>Acta Mathematica Scientia</source>, <year>2015</year>, <volume><strong>35</strong></volume> (<issue>2</issue>): <fpage>769</fpage>- <lpage>779</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sxwlxb201504013" target="_blank">URL</a> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8223"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b3')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b4" name="b4" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [4] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Feugainga</surname> <given-names>Gassa</given-names> </name>, <name> <surname>Crumeyrollea</surname> <given-names>O</given-names> </name>, <name> <surname>Yang</surname> <given-names>K S</given-names> </name>, <name> <surname>Mutabazia</surname> <given-names>I</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Destabilization of the Couette-Taylor flow by modulation of the inner cylinder rotation</p><source>European Journal of Mechanics-B/Fluids</source>, <year>2014</year>, <volume><strong>44</strong></volume>, <fpage>82</fpage>- <lpage>87</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="doi"> DOI:<a href="https://doi.org/10.1016/j.euromechflu.2013.10.006" target="_blank">10.1016/j.euromechflu.2013.10.006</a> </span> <span class="cited" id="bd_cited_count_"></span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b5" name="b5" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [5] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Ostilla</surname> <given-names>R</given-names> </name>, <name> <surname>Stevens</surname> <given-names>R</given-names> </name>, <name> <surname>Grossmann</surname> <given-names>S</given-names> </name>, <etal>et al</etal>. </person-group> <p class="cankaowenxian-xx-z">Optimal Taylor-Couette flow:Direct numerical simulations</p><source>Journal of Fluid Mechanics</source>, <year>2013</year>, <volume><strong>719</strong></volume>, <fpage>14</fpage>- <lpage>46</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="doi"> DOI:<a href="https://doi.org/10.1017/jfm.2012.596" target="_blank">10.1017/jfm.2012.596</a> </span> <span class="cited" id="bd_cited_count_"></span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b6" name="b6" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [6] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Wang</surname> <given-names>H Y</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Dynamical behaviors and numerical simulation of Lorenz systems for the incompressible flow between two concentric rotating cylinders</p><source>International Journal of Bifurcation and Chaos</source>, <year>2012</year>, <volume><strong>22</strong></volume> (<issue>5</issue>): <fpage>56</fpage>- <lpage>73</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1142/S0218127412501246" target="_blank">URL</a> <span class="cited" id="bd_cited_count_"></span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b7" name="b7" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [7] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="book"> <person-group person-group-type="author"> <name> <surname>Chossat</surname> <given-names>P</given-names> </name>, <name> <surname>Looss</surname> <given-names>G</given-names> </name>. </person-group> <source>The Couette-Taylor Problem</source>. <publisher-loc>New York</publisher-loc>: <publisher-name>Springer-Verlag</publisher-name>, <year>1994</year> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="cited" id="bd_cited_count_"></span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b8" name="b8" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [8] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="book"> <person-group person-group-type="author"> <name> <surname>Swinney</surname> <given-names>H L</given-names> </name>, <name> <surname>Gollub</surname> <given-names>J P</given-names> </name>. </person-group> <source>Hydrodynamic Instablilities and the Transition to Turbulence</source>. <publisher-loc>New York</publisher-loc>: <publisher-name>Springer-Verlag</publisher-name>, <year>1981</year> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="cited" id="bd_cited_count_"></span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b9" name="b9" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [9] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Taylor</surname> <given-names>G I</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Stability of a viscous liquid contained between two rotating cylinders</p><source>Phil Trans Roy Soc A</source>, <year>1923</year>, <volume><strong>223</strong></volume>, <fpage>289</fpage>- <lpage>343</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=S002211206400091X" target="_blank">URL</a> <span class="cited" id="bd_cited_count_"></span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b10" name="b10" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [10] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Thomas</surname> <given-names>D G</given-names> </name>, <name> <surname>Khomami</surname> <given-names>B</given-names> </name>, <name> <surname>Sureshkumar</surname> <given-names>R</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Nonlinear dynamics of viscoelastic Taylor-Couette flow, effect of elasticity on pattern selection, molecular conformation and drag</p><source>J Fluid Mech</source>, <year>2009</year>, <volume><strong>620</strong></volume>, <fpage>353</fpage>- <lpage>382</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="doi"> DOI:<a href="https://doi.org/10.1017/S0022112008004710" target="_blank">10.1017/S0022112008004710</a> </span> <span class="cited" id="bd_cited_count_"></span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b11" name="b11" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [11] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Anderreck</surname> <given-names>C D</given-names> </name>, <name> <surname>Liu</surname> <given-names>S S</given-names> </name>, <name> <surname>Swinney</surname> <given-names>H L</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Flow regimes in a circular Couette system with independent rotating cylinders</p><source>J Fluid Mech</source>, <year>1986</year>, <volume><strong>64</strong></volume>, <fpage>155</fpage>- <lpage>183</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="cited" id="bd_cited_count_"></span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b12" name="b12" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [12] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <string-name name-style="eastern">王贺元</string-name>, <string-name name-style="eastern">崔进</string-name>. </person-group> <p class="cankaowenxian-xx-z">旋转流动的低模分析及仿真研究</p><source>应用数学与力学</source>, <year>2017</year>, <volume><strong>38</strong></volume> (<issue>7</issue>): <fpage>794</fpage>- <lpage>806</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://d.old.wanfangdata.com.cn/Periodical/yysxhlx201707007" target="_blank">URL</a> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8232"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b12')" class="bianju"> [本文引用: 3]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal" xml:lang="en"> <person-group person-group-type="author"> <name> <surname>Wang</surname> <given-names>H Y</given-names> </name>, <name> <surname>Cui</surname> <given-names>Jin</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Low-dimensional analysis and numerical simulation of rotating flow</p><trans-source xml:lang="en">Applied Mathematics and Mechanics</trans-source>, <year>2017</year>, <volume><strong>38</strong></volume> (<issue>7</issue>): <fpage>794</fpage>- <lpage>806</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://d.old.wanfangdata.com.cn/Periodical/yysxhlx201707007" target="_blank">URL</a> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8233"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b12')" class="bianju"> [本文引用: 3]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b13" name="b13" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [13] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Arnold</surname> <given-names>V</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Kolmogorov'S hydrodynamic attractors</p><source>Proc R Soc Lond A</source>, <year>1991</year>, <volume><strong>434</strong></volume> (<issue>19</issue>): <fpage>19</fpage>- <lpage>22</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://cn.bing.com/academic/profile?id=1b5df541e63e3bca8e230060a9472f00&encoded=0&v=paper_preview&mkt=zh-cn" target="_blank">URL</a> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8234"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b13')" class="bianju"> [本文引用: 2]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b14" name="b14" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [14] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Pasini</surname> <given-names>A</given-names> </name>, <name> <surname>Pelino</surname> <given-names>V</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">A unified view of kolmogorov and lorenz systems</p><source>Phys Lett A</source>, <year>2000</year>, <volume><strong>275</strong></volume>, <fpage>435</fpage>- <lpage>446</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="doi"> DOI:<a href="https://doi.org/10.1016/S0375-9601(00)00620-4" target="_blank">10.1016/S0375-9601(00)00620-4</a> </span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8235"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b14')" class="bianju"> [本文引用: 2]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b15" name="b15" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [15] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Liang</surname> <given-names>X Y</given-names> </name>, <name> <surname>Qi</surname> <given-names>G Y</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Mechanical analysis and energy conversion of Chen chaotic system</p><source>General and Applied Physics</source>, <year>2017</year>, <volume><strong>47</strong></volume> (<issue>4</issue>): <fpage>288</fpage>- <lpage>294</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8236"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b15')" class="bianju"> [本文引用: 2]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b16" name="b16" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [16] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Liang</surname> <given-names>X Y</given-names> </name>, <name> <surname>Qi</surname> <given-names>G Y</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Mechanical analysis of Chen chaotic system</p><source>Chaos, Solitons and Fractals</source>, <year>2017</year>, <volume><strong>98</strong></volume>, <fpage>173</fpage>- <lpage>177</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="doi"> DOI:<a href="https://doi.org/10.1016/j.chaos.2017.03.021" target="_blank">10.1016/j.chaos.2017.03.021</a> </span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8237"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b16')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b17" name="b17" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [17] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Qi</surname> <given-names>G</given-names> </name>, <name> <surname>Liang</surname> <given-names>X</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Mechanical analysis of qi four-wing chaotic system</p><source>Nonlinear Dyn</source>, <year>2016</year>, <volume><strong>86</strong></volume> (<issue>2</issue>): <fpage>1095</fpage>- <lpage>1106</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a7a052e418975f4731ba24d12bdb811f" target="_blank">URL</a> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8238"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b17')" class="bianju"> [本文引用: 2]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b18" name="b18" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [18] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Pelino</surname> <given-names>V</given-names> </name>, <name> <surname>Maimone</surname> <given-names>F</given-names> </name>, <name> <surname>Pasini</surname> <given-names>A</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Energy cycle for the lorenz attractor</p><source>Chaos Soliton Fract</source>, <year>2014</year>, <volume><strong>64</strong></volume>, <fpage>67</fpage>- <lpage>77</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="doi"> DOI:<a href="https://doi.org/10.1016/j.chaos.2013.09.005" target="_blank">10.1016/j.chaos.2013.09.005</a> </span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8239"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b18')" class="bianju"> [本文引用: 4]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b19" name="b19" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [19] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="book"> <person-group person-group-type="author"> <name> <surname>Marsden</surname> <given-names>J</given-names> </name>, <name> <surname>Ratiu</surname> <given-names>T</given-names> </name>. </person-group> <source>Introduction to Mechanics and Symmetry:A Basic Exposition of Classical Mechanical Systems (2nd edn)</source>. <publisher-loc>Berlin</publisher-loc>: <publisher-name>Springer</publisher-name>, <year>2002</year> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8240"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b19')" class="bianju"> [本文引用: 4]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b20" name="b20" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [20] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="book"> <person-group person-group-type="author"> <name> <surname>Strogatz</surname> <given-names>S H</given-names> </name>. </person-group> <source>Nonlinear Dynamics and Chaos</source>. <publisher-loc>MA</publisher-loc>: <publisher-name>Perseus Books, Reading</publisher-name>, <year>1994</year> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8241"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b20')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b21" name="b21" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [21] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Morrison</surname> <given-names>P J</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Thoughts on brackets and dissipation:Old and new</p><source>Journal of Physics:Conference Series</source>, <year>2009</year>, <volume><strong>169</strong></volume> (<issue>1</issue>): <fpage>012006</fpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8242"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b21')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b22" name="b22" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [22] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Doering</surname> <given-names>C R</given-names> </name>, <name> <surname>Gibbon</surname> <given-names>J D</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">On the shape and dimension of the Lorenz attractor</p><source>Dyn Stab Syst</source>, <year>1995</year>, <volume><strong>10</strong></volume> (<issue>3</issue>): <fpage>255</fpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1080/02681119508806207" target="_blank">URL</a> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8243"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b22')" class="bianju"> [本文引用: 3]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> <div> <div id="article_reference_meta" style="display: none;"> <div id="article_reference_meta_b1"> <div id="article_reference_meta_b1_title" class="title_">A model study of stability of couette flow</div> <div id="article_reference_meta_b1_citedNumber">1</div> <div id="article_reference_meta_b1_nian">1987</div> <div id="article_reference_meta_b1_jcr"></div> <div id="article_reference_meta_b1_cjcr"></div> <div id="article_reference_meta_b1_articleCitedText"> <div class="sentence">... 同轴圆筒间旋转流动的Couette-Taylor流问题是近一个世纪以来人们普遍关注的热点问题,由于其流动形态的可观测性以及它在湍流研究中的基础性地位及其在流体机械、石油化工等领域的广泛应用,国际上将其列为非线性科学的范例之一.国内外众多学者对其复杂的动力学行为进行了大量深入的研究,相关文献非常丰富(文献[<xref ref-type="bibr" rid="b1">1</xref>-<xref ref-type="bibr" rid="b12">12</xref>]只是2000多篇文献中较少的一部分).如果内圆筒旋转,外圆筒静止,这种流动历经Couette流、Taylor涡流、Taylor行进波、波状螺旋漩涡、调制波状螺旋漩涡、湍状Taylor涡流等十几种波形最终进入湍流(见<xref ref-type="fig" rid="Fig1">图 1</xref>),如果内外圆筒同时正向或反向旋转,可以观察到更为丰富的流动,具体见文献[<xref ref-type="bibr" rid="b3">3</xref>-<xref ref-type="bibr" rid="b12">12</xref>]. ...</div> </div> </div> <div id="article_reference_meta_b2"> <div id="article_reference_meta_b2_title" class="title_">Lorenz systems for the incompressible flow between two concentric rotating cylinders</div> <div id="article_reference_meta_b2_citedNumber">1</div> <div id="article_reference_meta_b2_nian">2010</div> <div id="article_reference_meta_b2_jcr"></div> <div id="article_reference_meta_b2_cjcr"></div> <div id="article_reference_meta_b2_articleCitedText"> <div class="sentence">... 文献[<xref ref-type="bibr" rid="b2">2</xref>]利用同轴圆筒间隙区域Stokes算子的特征函数作为基函数对周期性边界条件Navier-Stokes方程进行傅里叶展开,将原偏微分方程组化为常微分方程组,取傅里叶级数的前三项,得到下列方程组 ...</div> </div> </div> <div id="article_reference_meta_b3"> <div id="article_reference_meta_b3_title" class="title_">The chaos behavior and simulation of three model systems of Couette-Taylor flow</div> <div id="article_reference_meta_b3_citedNumber">1</div> <div id="article_reference_meta_b3_nian">2015</div> <div id="article_reference_meta_b3_jcr"></div> <div id="article_reference_meta_b3_cjcr"></div> <div id="article_reference_meta_b3_articleCitedText"> <div class="sentence">... 同轴圆筒间旋转流动的Couette-Taylor流问题是近一个世纪以来人们普遍关注的热点问题,由于其流动形态的可观测性以及它在湍流研究中的基础性地位及其在流体机械、石油化工等领域的广泛应用,国际上将其列为非线性科学的范例之一.国内外众多学者对其复杂的动力学行为进行了大量深入的研究,相关文献非常丰富(文献[<xref ref-type="bibr" rid="b1">1</xref>-<xref ref-type="bibr" rid="b12">12</xref>]只是2000多篇文献中较少的一部分).如果内圆筒旋转,外圆筒静止,这种流动历经Couette流、Taylor涡流、Taylor行进波、波状螺旋漩涡、调制波状螺旋漩涡、湍状Taylor涡流等十几种波形最终进入湍流(见<xref ref-type="fig" rid="Fig1">图 1</xref>),如果内外圆筒同时正向或反向旋转,可以观察到更为丰富的流动,具体见文献[<xref ref-type="bibr" rid="b3">3</xref>-<xref ref-type="bibr" rid="b12">12</xref>]. ...</div> </div> </div> <div id="article_reference_meta_b4"> <div id="article_reference_meta_b4_title" class="title_">Destabilization of the Couette-Taylor flow by modulation of the inner cylinder rotation</div> <div id="article_reference_meta_b4_citedNumber">0</div> <div id="article_reference_meta_b4_nian">2014</div> <div id="article_reference_meta_b4_jcr"></div> <div id="article_reference_meta_b4_cjcr"></div> </div> <div id="article_reference_meta_b5"> <div id="article_reference_meta_b5_title" class="title_">Optimal Taylor-Couette flow:Direct numerical simulations</div> <div id="article_reference_meta_b5_citedNumber">0</div> <div id="article_reference_meta_b5_nian">2013</div> <div id="article_reference_meta_b5_jcr"></div> <div id="article_reference_meta_b5_cjcr"></div> </div> <div id="article_reference_meta_b6"> <div id="article_reference_meta_b6_title" class="title_">Dynamical behaviors and numerical simulation of Lorenz systems for the incompressible flow between two concentric rotating cylinders</div> <div id="article_reference_meta_b6_citedNumber">0</div> <div id="article_reference_meta_b6_nian">2012</div> <div id="article_reference_meta_b6_jcr"></div> <div id="article_reference_meta_b6_cjcr"></div> </div> <div id="article_reference_meta_b7"> <div id="article_reference_meta_b7_title" class="title_"></div> <div id="article_reference_meta_b7_citedNumber">0</div> <div id="article_reference_meta_b7_nian">1994</div> <div id="article_reference_meta_b7_jcr"></div> <div id="article_reference_meta_b7_cjcr"></div> </div> <div id="article_reference_meta_b8"> <div id="article_reference_meta_b8_title" class="title_"></div> <div id="article_reference_meta_b8_citedNumber">0</div> <div id="article_reference_meta_b8_nian">1981</div> <div id="article_reference_meta_b8_jcr"></div> <div id="article_reference_meta_b8_cjcr"></div> </div> <div id="article_reference_meta_b9"> <div id="article_reference_meta_b9_title" class="title_">Stability of a viscous liquid contained between two rotating cylinders</div> <div id="article_reference_meta_b9_citedNumber">0</div> <div id="article_reference_meta_b9_nian">1923</div> <div id="article_reference_meta_b9_jcr"></div> <div id="article_reference_meta_b9_cjcr"></div> </div> <div id="article_reference_meta_b10"> <div id="article_reference_meta_b10_title" class="title_">Nonlinear dynamics of viscoelastic Taylor-Couette flow, effect of elasticity on pattern selection, molecular conformation and drag</div> <div id="article_reference_meta_b10_citedNumber">0</div> <div id="article_reference_meta_b10_nian">2009</div> <div id="article_reference_meta_b10_jcr"></div> <div id="article_reference_meta_b10_cjcr"></div> </div> <div id="article_reference_meta_b11"> <div id="article_reference_meta_b11_title" class="title_">Flow regimes in a circular Couette system with independent rotating cylinders</div> <div id="article_reference_meta_b11_citedNumber">0</div> <div id="article_reference_meta_b11_nian">1986</div> <div id="article_reference_meta_b11_jcr"></div> <div id="article_reference_meta_b11_cjcr"></div> </div> <div id="article_reference_meta_b12"> <div id="article_reference_meta_b12_title" class="title_">旋转流动的低模分析及仿真研究</div> <div id="article_reference_meta_b12_citedNumber">3</div> <div id="article_reference_meta_b12_nian">2017</div> <div id="article_reference_meta_b12_jcr"></div> <div id="article_reference_meta_b12_cjcr"></div> <div id="article_reference_meta_b12_articleCitedText"> <div class="sentence">... 同轴圆筒间旋转流动的Couette-Taylor流问题是近一个世纪以来人们普遍关注的热点问题,由于其流动形态的可观测性以及它在湍流研究中的基础性地位及其在流体机械、石油化工等领域的广泛应用,国际上将其列为非线性科学的范例之一.国内外众多学者对其复杂的动力学行为进行了大量深入的研究,相关文献非常丰富(文献[<xref ref-type="bibr" rid="b1">1</xref>-<xref ref-type="bibr" rid="b12">12</xref>]只是2000多篇文献中较少的一部分).如果内圆筒旋转,外圆筒静止,这种流动历经Couette流、Taylor涡流、Taylor行进波、波状螺旋漩涡、调制波状螺旋漩涡、湍状Taylor涡流等十几种波形最终进入湍流(见<xref ref-type="fig" rid="Fig1">图 1</xref>),如果内外圆筒同时正向或反向旋转,可以观察到更为丰富的流动,具体见文献[<xref ref-type="bibr" rid="b3">3</xref>-<xref ref-type="bibr" rid="b12">12</xref>]. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... -<xref ref-type="bibr" rid="b12">12</xref>]. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 混沌系统按其各项及相互作用是相当复杂的.如果从力学角度对混沌进行研究,可以从中发现更多的混沌基本成因.从力学角度研究混沌系统已经有了良好的开端,阿诺德<sup>[<xref ref-type="bibr" rid="b13">13</xref>]</sup>用Kolmogorov系统来描述具有哈密顿函数的不同的强迫动力系统,流体动力系统等. Pasini和Pelino<sup>[<xref ref-type="bibr" rid="b14">14</xref>]</sup>对Lorenz系统进行了研究,并给出了统一的柯尔莫哥洛夫(Kolmogorov)和洛伦茨(Lorenz)系统.齐和梁<sup>[<xref ref-type="bibr" rid="b15">15</xref>]</sup>引进Casimir函数分析了Chen混沌系统的动力学行为和能量转换,揭示了能量转换和轨道与平衡点间的距离,并估计了混沌吸引子的界.文献[<xref ref-type="bibr" rid="b16">16</xref>]研究了Chen混沌系统力学机理与能量转换,将Chen混沌系统转换成Kolmogorov形系统,通过不同力矩的结合分析和研究了Chen混沌系统产生混沌的关键因素和物理意义.研究了哈密顿能量,动能和势能之间的相互转换.讨论了能量与雷诺数之间的关系.文献[<xref ref-type="bibr" rid="b17">17</xref>]研究了齐四翼混沌系统的力学机理与能量转换,通过与Kolmogorov系统和欧拉方程的比较,把四翼混沌系统的矢量场分解为惯性力矩、内力矩、耗散和外力矩来探讨产生混沌的基本因素.利用Lie-Poisson括号揭示哈密顿能,动能与势能的相互转换.通过五种情形分析研究了四翼混沌吸引子不同类型力矩的功能和作用以及产生不同类型动力学模式的关键因素.此外,借助扩展的Kolmogorov系统, Pelino等<sup>[<xref ref-type="bibr" rid="b18">18</xref>]</sup>研究了洛伦兹系统的能量转换.上述几篇文献开启了从力学角度研究混沌系统的先河,但文献[<xref ref-type="bibr" rid="b15">15</xref>-<xref ref-type="bibr" rid="b17">17</xref>]中的混沌系统均为数值混沌系统(通过数值计算发现的混沌系统),没有明确的物理意义.借鉴这三篇文献的思想和方法我们探讨了具有明确物理意义的Couette-Taylor流问题,讨论的Couette-Taylor流三模混沌系统属于物理混沌系统(具有物理背景和物理意义的混沌系统),研究了Couette-Taylor流的动力机制,物理意义和能量转换.把Couette-Taylor流三模态系统(见文献[<xref ref-type="bibr" rid="b12">12</xref>])的状态变量视为角动量,将矢量场分解为惯性力矩,内转矩,耗散力矩和外力矩,不同的力矩的耦合视为不同的动力模式,通过分析各种力矩与Couette-Taylor流的不同模态的因果关系,揭示各种Taylor涡和混沌生成的力学机理.从力学角度分析同轴圆筒间旋转流动的各种涡流和混沌的生成机理目前还没有文献涉及. ...</div> </div> </div> <div id="article_reference_meta_b12"> <div id="article_reference_meta_b12_title" class="title_">旋转流动的低模分析及仿真研究</div> <div id="article_reference_meta_b12_citedNumber">3</div> <div id="article_reference_meta_b12_nian">2017</div> <div id="article_reference_meta_b12_jcr"></div> <div id="article_reference_meta_b12_cjcr"></div> <div id="article_reference_meta_b12_articleCitedText"> <div class="sentence">... 同轴圆筒间旋转流动的Couette-Taylor流问题是近一个世纪以来人们普遍关注的热点问题,由于其流动形态的可观测性以及它在湍流研究中的基础性地位及其在流体机械、石油化工等领域的广泛应用,国际上将其列为非线性科学的范例之一.国内外众多学者对其复杂的动力学行为进行了大量深入的研究,相关文献非常丰富(文献[<xref ref-type="bibr" rid="b1">1</xref>-<xref ref-type="bibr" rid="b12">12</xref>]只是2000多篇文献中较少的一部分).如果内圆筒旋转,外圆筒静止,这种流动历经Couette流、Taylor涡流、Taylor行进波、波状螺旋漩涡、调制波状螺旋漩涡、湍状Taylor涡流等十几种波形最终进入湍流(见<xref ref-type="fig" rid="Fig1">图 1</xref>),如果内外圆筒同时正向或反向旋转,可以观察到更为丰富的流动,具体见文献[<xref ref-type="bibr" rid="b3">3</xref>-<xref ref-type="bibr" rid="b12">12</xref>]. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... -<xref ref-type="bibr" rid="b12">12</xref>]. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 混沌系统按其各项及相互作用是相当复杂的.如果从力学角度对混沌进行研究,可以从中发现更多的混沌基本成因.从力学角度研究混沌系统已经有了良好的开端,阿诺德<sup>[<xref ref-type="bibr" rid="b13">13</xref>]</sup>用Kolmogorov系统来描述具有哈密顿函数的不同的强迫动力系统,流体动力系统等. Pasini和Pelino<sup>[<xref ref-type="bibr" rid="b14">14</xref>]</sup>对Lorenz系统进行了研究,并给出了统一的柯尔莫哥洛夫(Kolmogorov)和洛伦茨(Lorenz)系统.齐和梁<sup>[<xref ref-type="bibr" rid="b15">15</xref>]</sup>引进Casimir函数分析了Chen混沌系统的动力学行为和能量转换,揭示了能量转换和轨道与平衡点间的距离,并估计了混沌吸引子的界.文献[<xref ref-type="bibr" rid="b16">16</xref>]研究了Chen混沌系统力学机理与能量转换,将Chen混沌系统转换成Kolmogorov形系统,通过不同力矩的结合分析和研究了Chen混沌系统产生混沌的关键因素和物理意义.研究了哈密顿能量,动能和势能之间的相互转换.讨论了能量与雷诺数之间的关系.文献[<xref ref-type="bibr" rid="b17">17</xref>]研究了齐四翼混沌系统的力学机理与能量转换,通过与Kolmogorov系统和欧拉方程的比较,把四翼混沌系统的矢量场分解为惯性力矩、内力矩、耗散和外力矩来探讨产生混沌的基本因素.利用Lie-Poisson括号揭示哈密顿能,动能与势能的相互转换.通过五种情形分析研究了四翼混沌吸引子不同类型力矩的功能和作用以及产生不同类型动力学模式的关键因素.此外,借助扩展的Kolmogorov系统, Pelino等<sup>[<xref ref-type="bibr" rid="b18">18</xref>]</sup>研究了洛伦兹系统的能量转换.上述几篇文献开启了从力学角度研究混沌系统的先河,但文献[<xref ref-type="bibr" rid="b15">15</xref>-<xref ref-type="bibr" rid="b17">17</xref>]中的混沌系统均为数值混沌系统(通过数值计算发现的混沌系统),没有明确的物理意义.借鉴这三篇文献的思想和方法我们探讨了具有明确物理意义的Couette-Taylor流问题,讨论的Couette-Taylor流三模混沌系统属于物理混沌系统(具有物理背景和物理意义的混沌系统),研究了Couette-Taylor流的动力机制,物理意义和能量转换.把Couette-Taylor流三模态系统(见文献[<xref ref-type="bibr" rid="b12">12</xref>])的状态变量视为角动量,将矢量场分解为惯性力矩,内转矩,耗散力矩和外力矩,不同的力矩的耦合视为不同的动力模式,通过分析各种力矩与Couette-Taylor流的不同模态的因果关系,揭示各种Taylor涡和混沌生成的力学机理.从力学角度分析同轴圆筒间旋转流动的各种涡流和混沌的生成机理目前还没有文献涉及. ...</div> </div> </div> <div id="article_reference_meta_b13"> <div id="article_reference_meta_b13_title" class="title_">Kolmogorov'S hydrodynamic attractors</div> <div id="article_reference_meta_b13_citedNumber">2</div> <div id="article_reference_meta_b13_nian">1991</div> <div id="article_reference_meta_b13_jcr"></div> <div id="article_reference_meta_b13_cjcr"></div> <div id="article_reference_meta_b13_articleCitedText"> <div class="sentence">... 混沌系统按其各项及相互作用是相当复杂的.如果从力学角度对混沌进行研究,可以从中发现更多的混沌基本成因.从力学角度研究混沌系统已经有了良好的开端,阿诺德<sup>[<xref ref-type="bibr" rid="b13">13</xref>]</sup>用Kolmogorov系统来描述具有哈密顿函数的不同的强迫动力系统,流体动力系统等. Pasini和Pelino<sup>[<xref ref-type="bibr" rid="b14">14</xref>]</sup>对Lorenz系统进行了研究,并给出了统一的柯尔莫哥洛夫(Kolmogorov)和洛伦茨(Lorenz)系统.齐和梁<sup>[<xref ref-type="bibr" rid="b15">15</xref>]</sup>引进Casimir函数分析了Chen混沌系统的动力学行为和能量转换,揭示了能量转换和轨道与平衡点间的距离,并估计了混沌吸引子的界.文献[<xref ref-type="bibr" rid="b16">16</xref>]研究了Chen混沌系统力学机理与能量转换,将Chen混沌系统转换成Kolmogorov形系统,通过不同力矩的结合分析和研究了Chen混沌系统产生混沌的关键因素和物理意义.研究了哈密顿能量,动能和势能之间的相互转换.讨论了能量与雷诺数之间的关系.文献[<xref ref-type="bibr" rid="b17">17</xref>]研究了齐四翼混沌系统的力学机理与能量转换,通过与Kolmogorov系统和欧拉方程的比较,把四翼混沌系统的矢量场分解为惯性力矩、内力矩、耗散和外力矩来探讨产生混沌的基本因素.利用Lie-Poisson括号揭示哈密顿能,动能与势能的相互转换.通过五种情形分析研究了四翼混沌吸引子不同类型力矩的功能和作用以及产生不同类型动力学模式的关键因素.此外,借助扩展的Kolmogorov系统, Pelino等<sup>[<xref ref-type="bibr" rid="b18">18</xref>]</sup>研究了洛伦兹系统的能量转换.上述几篇文献开启了从力学角度研究混沌系统的先河,但文献[<xref ref-type="bibr" rid="b15">15</xref>-<xref ref-type="bibr" rid="b17">17</xref>]中的混沌系统均为数值混沌系统(通过数值计算发现的混沌系统),没有明确的物理意义.借鉴这三篇文献的思想和方法我们探讨了具有明确物理意义的Couette-Taylor流问题,讨论的Couette-Taylor流三模混沌系统属于物理混沌系统(具有物理背景和物理意义的混沌系统),研究了Couette-Taylor流的动力机制,物理意义和能量转换.把Couette-Taylor流三模态系统(见文献[<xref ref-type="bibr" rid="b12">12</xref>])的状态变量视为角动量,将矢量场分解为惯性力矩,内转矩,耗散力矩和外力矩,不同的力矩的耦合视为不同的动力模式,通过分析各种力矩与Couette-Taylor流的不同模态的因果关系,揭示各种Taylor涡和混沌生成的力学机理.从力学角度分析同轴圆筒间旋转流动的各种涡流和混沌的生成机理目前还没有文献涉及. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 系统(2.2)是Kolmogorov描述具有哈密顿函数的不同强迫动力系统,流体动力系统等引入的<sup>[<xref ref-type="bibr" rid="b13">13</xref>]</sup>.在欧拉方程中力(或力矩)<span class="formulaText"><inline-formula><tex-math id="M19">$ \{X, H\} $</tex-math></inline-formula></span>是惯性力(离心力).系统(2.2)是具有耗散力和外力的广义欧拉方程<sup>[<xref ref-type="bibr" rid="b19">19</xref>]</sup>.经变量变换<span class="formulaText"><inline-formula><tex-math id="M21">$ x\mapsto x, y\mapsto y, z\mapsto z-ar- c $</tex-math></inline-formula></span>,系统(2.1)化为 ...</div> </div> </div> <div id="article_reference_meta_b14"> <div id="article_reference_meta_b14_title" class="title_">A unified view of kolmogorov and lorenz systems</div> <div id="article_reference_meta_b14_citedNumber">2</div> <div id="article_reference_meta_b14_nian">2000</div> <div id="article_reference_meta_b14_jcr"></div> <div id="article_reference_meta_b14_cjcr"></div> <div id="article_reference_meta_b14_articleCitedText"> <div class="sentence">... 混沌系统按其各项及相互作用是相当复杂的.如果从力学角度对混沌进行研究,可以从中发现更多的混沌基本成因.从力学角度研究混沌系统已经有了良好的开端,阿诺德<sup>[<xref ref-type="bibr" rid="b13">13</xref>]</sup>用Kolmogorov系统来描述具有哈密顿函数的不同的强迫动力系统,流体动力系统等. Pasini和Pelino<sup>[<xref ref-type="bibr" rid="b14">14</xref>]</sup>对Lorenz系统进行了研究,并给出了统一的柯尔莫哥洛夫(Kolmogorov)和洛伦茨(Lorenz)系统.齐和梁<sup>[<xref ref-type="bibr" rid="b15">15</xref>]</sup>引进Casimir函数分析了Chen混沌系统的动力学行为和能量转换,揭示了能量转换和轨道与平衡点间的距离,并估计了混沌吸引子的界.文献[<xref ref-type="bibr" rid="b16">16</xref>]研究了Chen混沌系统力学机理与能量转换,将Chen混沌系统转换成Kolmogorov形系统,通过不同力矩的结合分析和研究了Chen混沌系统产生混沌的关键因素和物理意义.研究了哈密顿能量,动能和势能之间的相互转换.讨论了能量与雷诺数之间的关系.文献[<xref ref-type="bibr" rid="b17">17</xref>]研究了齐四翼混沌系统的力学机理与能量转换,通过与Kolmogorov系统和欧拉方程的比较,把四翼混沌系统的矢量场分解为惯性力矩、内力矩、耗散和外力矩来探讨产生混沌的基本因素.利用Lie-Poisson括号揭示哈密顿能,动能与势能的相互转换.通过五种情形分析研究了四翼混沌吸引子不同类型力矩的功能和作用以及产生不同类型动力学模式的关键因素.此外,借助扩展的Kolmogorov系统, Pelino等<sup>[<xref ref-type="bibr" rid="b18">18</xref>]</sup>研究了洛伦兹系统的能量转换.上述几篇文献开启了从力学角度研究混沌系统的先河,但文献[<xref ref-type="bibr" rid="b15">15</xref>-<xref ref-type="bibr" rid="b17">17</xref>]中的混沌系统均为数值混沌系统(通过数值计算发现的混沌系统),没有明确的物理意义.借鉴这三篇文献的思想和方法我们探讨了具有明确物理意义的Couette-Taylor流问题,讨论的Couette-Taylor流三模混沌系统属于物理混沌系统(具有物理背景和物理意义的混沌系统),研究了Couette-Taylor流的动力机制,物理意义和能量转换.把Couette-Taylor流三模态系统(见文献[<xref ref-type="bibr" rid="b12">12</xref>])的状态变量视为角动量,将矢量场分解为惯性力矩,内转矩,耗散力矩和外力矩,不同的力矩的耦合视为不同的动力模式,通过分析各种力矩与Couette-Taylor流的不同模态的因果关系,揭示各种Taylor涡和混沌生成的力学机理.从力学角度分析同轴圆筒间旋转流动的各种涡流和混沌的生成机理目前还没有文献涉及. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 不同于文献[<xref ref-type="bibr" rid="b14">14</xref>, <xref ref-type="bibr" rid="b18">18</xref>]中讨论的Kolmogorov系统,我们不能通过哈密顿函数的导数来确定能量耗散. <xref ref-type="fig" rid="Fig4">图 4 (a)</xref>给出了哈密顿函数<span class="formulaText"><inline-formula><tex-math id="M47">$ H $</tex-math></inline-formula></span>的时间演化,显示能量是耗散的,因为体积<span class="formulaText"><inline-formula><tex-math id="M48">$ V $</tex-math></inline-formula></span>耗散从而能量减少,如<xref ref-type="fig" rid="Fig4">图 4(b)</xref>所示. ...</div> </div> </div> <div id="article_reference_meta_b15"> <div id="article_reference_meta_b15_title" class="title_">Mechanical analysis and energy conversion of Chen chaotic system</div> <div id="article_reference_meta_b15_citedNumber">2</div> <div id="article_reference_meta_b15_nian">2017</div> <div id="article_reference_meta_b15_jcr"></div> <div id="article_reference_meta_b15_cjcr"></div> <div id="article_reference_meta_b15_articleCitedText"> <div class="sentence">... 混沌系统按其各项及相互作用是相当复杂的.如果从力学角度对混沌进行研究,可以从中发现更多的混沌基本成因.从力学角度研究混沌系统已经有了良好的开端,阿诺德<sup>[<xref ref-type="bibr" rid="b13">13</xref>]</sup>用Kolmogorov系统来描述具有哈密顿函数的不同的强迫动力系统,流体动力系统等. Pasini和Pelino<sup>[<xref ref-type="bibr" rid="b14">14</xref>]</sup>对Lorenz系统进行了研究,并给出了统一的柯尔莫哥洛夫(Kolmogorov)和洛伦茨(Lorenz)系统.齐和梁<sup>[<xref ref-type="bibr" rid="b15">15</xref>]</sup>引进Casimir函数分析了Chen混沌系统的动力学行为和能量转换,揭示了能量转换和轨道与平衡点间的距离,并估计了混沌吸引子的界.文献[<xref ref-type="bibr" rid="b16">16</xref>]研究了Chen混沌系统力学机理与能量转换,将Chen混沌系统转换成Kolmogorov形系统,通过不同力矩的结合分析和研究了Chen混沌系统产生混沌的关键因素和物理意义.研究了哈密顿能量,动能和势能之间的相互转换.讨论了能量与雷诺数之间的关系.文献[<xref ref-type="bibr" rid="b17">17</xref>]研究了齐四翼混沌系统的力学机理与能量转换,通过与Kolmogorov系统和欧拉方程的比较,把四翼混沌系统的矢量场分解为惯性力矩、内力矩、耗散和外力矩来探讨产生混沌的基本因素.利用Lie-Poisson括号揭示哈密顿能,动能与势能的相互转换.通过五种情形分析研究了四翼混沌吸引子不同类型力矩的功能和作用以及产生不同类型动力学模式的关键因素.此外,借助扩展的Kolmogorov系统, Pelino等<sup>[<xref ref-type="bibr" rid="b18">18</xref>]</sup>研究了洛伦兹系统的能量转换.上述几篇文献开启了从力学角度研究混沌系统的先河,但文献[<xref ref-type="bibr" rid="b15">15</xref>-<xref ref-type="bibr" rid="b17">17</xref>]中的混沌系统均为数值混沌系统(通过数值计算发现的混沌系统),没有明确的物理意义.借鉴这三篇文献的思想和方法我们探讨了具有明确物理意义的Couette-Taylor流问题,讨论的Couette-Taylor流三模混沌系统属于物理混沌系统(具有物理背景和物理意义的混沌系统),研究了Couette-Taylor流的动力机制,物理意义和能量转换.把Couette-Taylor流三模态系统(见文献[<xref ref-type="bibr" rid="b12">12</xref>])的状态变量视为角动量,将矢量场分解为惯性力矩,内转矩,耗散力矩和外力矩,不同的力矩的耦合视为不同的动力模式,通过分析各种力矩与Couette-Taylor流的不同模态的因果关系,揭示各种Taylor涡和混沌生成的力学机理.从力学角度分析同轴圆筒间旋转流动的各种涡流和混沌的生成机理目前还没有文献涉及. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 研究了洛伦兹系统的能量转换.上述几篇文献开启了从力学角度研究混沌系统的先河,但文献[<xref ref-type="bibr" rid="b15">15</xref>-<xref ref-type="bibr" rid="b17">17</xref>]中的混沌系统均为数值混沌系统(通过数值计算发现的混沌系统),没有明确的物理意义.借鉴这三篇文献的思想和方法我们探讨了具有明确物理意义的Couette-Taylor流问题,讨论的Couette-Taylor流三模混沌系统属于物理混沌系统(具有物理背景和物理意义的混沌系统),研究了Couette-Taylor流的动力机制,物理意义和能量转换.把Couette-Taylor流三模态系统(见文献[<xref ref-type="bibr" rid="b12">12</xref>])的状态变量视为角动量,将矢量场分解为惯性力矩,内转矩,耗散力矩和外力矩,不同的力矩的耦合视为不同的动力模式,通过分析各种力矩与Couette-Taylor流的不同模态的因果关系,揭示各种Taylor涡和混沌生成的力学机理.从力学角度分析同轴圆筒间旋转流动的各种涡流和混沌的生成机理目前还没有文献涉及. ...</div> </div> </div> <div id="article_reference_meta_b16"> <div id="article_reference_meta_b16_title" class="title_">Mechanical analysis of Chen chaotic system</div> <div id="article_reference_meta_b16_citedNumber">1</div> <div id="article_reference_meta_b16_nian">2017</div> <div id="article_reference_meta_b16_jcr"></div> <div id="article_reference_meta_b16_cjcr"></div> <div id="article_reference_meta_b16_articleCitedText"> <div class="sentence">... 混沌系统按其各项及相互作用是相当复杂的.如果从力学角度对混沌进行研究,可以从中发现更多的混沌基本成因.从力学角度研究混沌系统已经有了良好的开端,阿诺德<sup>[<xref ref-type="bibr" rid="b13">13</xref>]</sup>用Kolmogorov系统来描述具有哈密顿函数的不同的强迫动力系统,流体动力系统等. Pasini和Pelino<sup>[<xref ref-type="bibr" rid="b14">14</xref>]</sup>对Lorenz系统进行了研究,并给出了统一的柯尔莫哥洛夫(Kolmogorov)和洛伦茨(Lorenz)系统.齐和梁<sup>[<xref ref-type="bibr" rid="b15">15</xref>]</sup>引进Casimir函数分析了Chen混沌系统的动力学行为和能量转换,揭示了能量转换和轨道与平衡点间的距离,并估计了混沌吸引子的界.文献[<xref ref-type="bibr" rid="b16">16</xref>]研究了Chen混沌系统力学机理与能量转换,将Chen混沌系统转换成Kolmogorov形系统,通过不同力矩的结合分析和研究了Chen混沌系统产生混沌的关键因素和物理意义.研究了哈密顿能量,动能和势能之间的相互转换.讨论了能量与雷诺数之间的关系.文献[<xref ref-type="bibr" rid="b17">17</xref>]研究了齐四翼混沌系统的力学机理与能量转换,通过与Kolmogorov系统和欧拉方程的比较,把四翼混沌系统的矢量场分解为惯性力矩、内力矩、耗散和外力矩来探讨产生混沌的基本因素.利用Lie-Poisson括号揭示哈密顿能,动能与势能的相互转换.通过五种情形分析研究了四翼混沌吸引子不同类型力矩的功能和作用以及产生不同类型动力学模式的关键因素.此外,借助扩展的Kolmogorov系统, Pelino等<sup>[<xref ref-type="bibr" rid="b18">18</xref>]</sup>研究了洛伦兹系统的能量转换.上述几篇文献开启了从力学角度研究混沌系统的先河,但文献[<xref ref-type="bibr" rid="b15">15</xref>-<xref ref-type="bibr" rid="b17">17</xref>]中的混沌系统均为数值混沌系统(通过数值计算发现的混沌系统),没有明确的物理意义.借鉴这三篇文献的思想和方法我们探讨了具有明确物理意义的Couette-Taylor流问题,讨论的Couette-Taylor流三模混沌系统属于物理混沌系统(具有物理背景和物理意义的混沌系统),研究了Couette-Taylor流的动力机制,物理意义和能量转换.把Couette-Taylor流三模态系统(见文献[<xref ref-type="bibr" rid="b12">12</xref>])的状态变量视为角动量,将矢量场分解为惯性力矩,内转矩,耗散力矩和外力矩,不同的力矩的耦合视为不同的动力模式,通过分析各种力矩与Couette-Taylor流的不同模态的因果关系,揭示各种Taylor涡和混沌生成的力学机理.从力学角度分析同轴圆筒间旋转流动的各种涡流和混沌的生成机理目前还没有文献涉及. ...</div> </div> </div> <div id="article_reference_meta_b17"> <div id="article_reference_meta_b17_title" class="title_">Mechanical analysis of qi four-wing chaotic system</div> <div id="article_reference_meta_b17_citedNumber">2</div> <div id="article_reference_meta_b17_nian">2016</div> <div id="article_reference_meta_b17_jcr"></div> <div id="article_reference_meta_b17_cjcr"></div> <div id="article_reference_meta_b17_articleCitedText"> <div class="sentence">... 混沌系统按其各项及相互作用是相当复杂的.如果从力学角度对混沌进行研究,可以从中发现更多的混沌基本成因.从力学角度研究混沌系统已经有了良好的开端,阿诺德<sup>[<xref ref-type="bibr" rid="b13">13</xref>]</sup>用Kolmogorov系统来描述具有哈密顿函数的不同的强迫动力系统,流体动力系统等. Pasini和Pelino<sup>[<xref ref-type="bibr" rid="b14">14</xref>]</sup>对Lorenz系统进行了研究,并给出了统一的柯尔莫哥洛夫(Kolmogorov)和洛伦茨(Lorenz)系统.齐和梁<sup>[<xref ref-type="bibr" rid="b15">15</xref>]</sup>引进Casimir函数分析了Chen混沌系统的动力学行为和能量转换,揭示了能量转换和轨道与平衡点间的距离,并估计了混沌吸引子的界.文献[<xref ref-type="bibr" rid="b16">16</xref>]研究了Chen混沌系统力学机理与能量转换,将Chen混沌系统转换成Kolmogorov形系统,通过不同力矩的结合分析和研究了Chen混沌系统产生混沌的关键因素和物理意义.研究了哈密顿能量,动能和势能之间的相互转换.讨论了能量与雷诺数之间的关系.文献[<xref ref-type="bibr" rid="b17">17</xref>]研究了齐四翼混沌系统的力学机理与能量转换,通过与Kolmogorov系统和欧拉方程的比较,把四翼混沌系统的矢量场分解为惯性力矩、内力矩、耗散和外力矩来探讨产生混沌的基本因素.利用Lie-Poisson括号揭示哈密顿能,动能与势能的相互转换.通过五种情形分析研究了四翼混沌吸引子不同类型力矩的功能和作用以及产生不同类型动力学模式的关键因素.此外,借助扩展的Kolmogorov系统, Pelino等<sup>[<xref ref-type="bibr" rid="b18">18</xref>]</sup>研究了洛伦兹系统的能量转换.上述几篇文献开启了从力学角度研究混沌系统的先河,但文献[<xref ref-type="bibr" rid="b15">15</xref>-<xref ref-type="bibr" rid="b17">17</xref>]中的混沌系统均为数值混沌系统(通过数值计算发现的混沌系统),没有明确的物理意义.借鉴这三篇文献的思想和方法我们探讨了具有明确物理意义的Couette-Taylor流问题,讨论的Couette-Taylor流三模混沌系统属于物理混沌系统(具有物理背景和物理意义的混沌系统),研究了Couette-Taylor流的动力机制,物理意义和能量转换.把Couette-Taylor流三模态系统(见文献[<xref ref-type="bibr" rid="b12">12</xref>])的状态变量视为角动量,将矢量场分解为惯性力矩,内转矩,耗散力矩和外力矩,不同的力矩的耦合视为不同的动力模式,通过分析各种力矩与Couette-Taylor流的不同模态的因果关系,揭示各种Taylor涡和混沌生成的力学机理.从力学角度分析同轴圆筒间旋转流动的各种涡流和混沌的生成机理目前还没有文献涉及. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... -<xref ref-type="bibr" rid="b17">17</xref>]中的混沌系统均为数值混沌系统(通过数值计算发现的混沌系统),没有明确的物理意义.借鉴这三篇文献的思想和方法我们探讨了具有明确物理意义的Couette-Taylor流问题,讨论的Couette-Taylor流三模混沌系统属于物理混沌系统(具有物理背景和物理意义的混沌系统),研究了Couette-Taylor流的动力机制,物理意义和能量转换.把Couette-Taylor流三模态系统(见文献[<xref ref-type="bibr" rid="b12">12</xref>])的状态变量视为角动量,将矢量场分解为惯性力矩,内转矩,耗散力矩和外力矩,不同的力矩的耦合视为不同的动力模式,通过分析各种力矩与Couette-Taylor流的不同模态的因果关系,揭示各种Taylor涡和混沌生成的力学机理.从力学角度分析同轴圆筒间旋转流动的各种涡流和混沌的生成机理目前还没有文献涉及. ...</div> </div> </div> <div id="article_reference_meta_b18"> <div id="article_reference_meta_b18_title" class="title_">Energy cycle for the lorenz attractor</div> <div id="article_reference_meta_b18_citedNumber">4</div> <div id="article_reference_meta_b18_nian">2014</div> <div id="article_reference_meta_b18_jcr"></div> <div id="article_reference_meta_b18_cjcr"></div> <div id="article_reference_meta_b18_articleCitedText"> <div class="sentence">... 混沌系统按其各项及相互作用是相当复杂的.如果从力学角度对混沌进行研究,可以从中发现更多的混沌基本成因.从力学角度研究混沌系统已经有了良好的开端,阿诺德<sup>[<xref ref-type="bibr" rid="b13">13</xref>]</sup>用Kolmogorov系统来描述具有哈密顿函数的不同的强迫动力系统,流体动力系统等. Pasini和Pelino<sup>[<xref ref-type="bibr" rid="b14">14</xref>]</sup>对Lorenz系统进行了研究,并给出了统一的柯尔莫哥洛夫(Kolmogorov)和洛伦茨(Lorenz)系统.齐和梁<sup>[<xref ref-type="bibr" rid="b15">15</xref>]</sup>引进Casimir函数分析了Chen混沌系统的动力学行为和能量转换,揭示了能量转换和轨道与平衡点间的距离,并估计了混沌吸引子的界.文献[<xref ref-type="bibr" rid="b16">16</xref>]研究了Chen混沌系统力学机理与能量转换,将Chen混沌系统转换成Kolmogorov形系统,通过不同力矩的结合分析和研究了Chen混沌系统产生混沌的关键因素和物理意义.研究了哈密顿能量,动能和势能之间的相互转换.讨论了能量与雷诺数之间的关系.文献[<xref ref-type="bibr" rid="b17">17</xref>]研究了齐四翼混沌系统的力学机理与能量转换,通过与Kolmogorov系统和欧拉方程的比较,把四翼混沌系统的矢量场分解为惯性力矩、内力矩、耗散和外力矩来探讨产生混沌的基本因素.利用Lie-Poisson括号揭示哈密顿能,动能与势能的相互转换.通过五种情形分析研究了四翼混沌吸引子不同类型力矩的功能和作用以及产生不同类型动力学模式的关键因素.此外,借助扩展的Kolmogorov系统, Pelino等<sup>[<xref ref-type="bibr" rid="b18">18</xref>]</sup>研究了洛伦兹系统的能量转换.上述几篇文献开启了从力学角度研究混沌系统的先河,但文献[<xref ref-type="bibr" rid="b15">15</xref>-<xref ref-type="bibr" rid="b17">17</xref>]中的混沌系统均为数值混沌系统(通过数值计算发现的混沌系统),没有明确的物理意义.借鉴这三篇文献的思想和方法我们探讨了具有明确物理意义的Couette-Taylor流问题,讨论的Couette-Taylor流三模混沌系统属于物理混沌系统(具有物理背景和物理意义的混沌系统),研究了Couette-Taylor流的动力机制,物理意义和能量转换.把Couette-Taylor流三模态系统(见文献[<xref ref-type="bibr" rid="b12">12</xref>])的状态变量视为角动量,将矢量场分解为惯性力矩,内转矩,耗散力矩和外力矩,不同的力矩的耦合视为不同的动力模式,通过分析各种力矩与Couette-Taylor流的不同模态的因果关系,揭示各种Taylor涡和混沌生成的力学机理.从力学角度分析同轴圆筒间旋转流动的各种涡流和混沌的生成机理目前还没有文献涉及. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 由于Couette-Taylor流的全局吸引子是非常复杂和难于计算的. Couette-Taylor流系统的轨道从一个不稳定的平衡点移动到另一个不稳定的平衡点,相应地,轨道和平衡点之间的距离随参数和时间的不同而变化.我们发现,卡西米尔(Casimir)函数与距离有密切关系,关于洛伦茨吸引子的可预测性和能量可以通过能量转换来进行研究<sup>[<xref ref-type="bibr" rid="b18">18</xref>]</sup>.因此,通过引入卡西米尔函数的导数,我们给出了Couette-Taylor流系统的能量转换,并且分析了它们的动力学和能量转换. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 不同于文献[<xref ref-type="bibr" rid="b14">14</xref>, <xref ref-type="bibr" rid="b18">18</xref>]中讨论的Kolmogorov系统,我们不能通过哈密顿函数的导数来确定能量耗散. <xref ref-type="fig" rid="Fig4">图 4 (a)</xref>给出了哈密顿函数<span class="formulaText"><inline-formula><tex-math id="M47">$ H $</tex-math></inline-formula></span>的时间演化,显示能量是耗散的,因为体积<span class="formulaText"><inline-formula><tex-math id="M48">$ V $</tex-math></inline-formula></span>耗散从而能量减少,如<xref ref-type="fig" rid="Fig4">图 4(b)</xref>所示. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 虽然Couette-Taylor流混沌系统与Lorenz系统不同,但能量转换时间演化与文献[<xref ref-type="bibr" rid="b18">18</xref>]的结果相似,能量、西米尔函数以及<span class="formulaText"><inline-formula><tex-math id="M153">$ D_1 $</tex-math></inline-formula></span>与<span class="formulaText"><inline-formula><tex-math id="M154">$ D_2 $</tex-math></inline-formula></span>的距离之和与外力矩(雷诺数<span class="formulaText"><inline-formula><tex-math id="M155">$ r $</tex-math></inline-formula></span><span class="formulaNumber">)</span>间的演化关系是本文的重要发现. ...</div> </div> </div> <div id="article_reference_meta_b19"> <div id="article_reference_meta_b19_title" class="title_"></div> <div id="article_reference_meta_b19_citedNumber">4</div> <div id="article_reference_meta_b19_nian">2002</div> <div id="article_reference_meta_b19_jcr"></div> <div id="article_reference_meta_b19_cjcr"></div> <div id="article_reference_meta_b19_articleCitedText"> <div class="sentence">... 其中<span class="formulaText"><inline-formula><tex-math id="M13">$ X = [x, y, z]^T $</tex-math></inline-formula></span>,反对称括号<span class="formulaText"><inline-formula><tex-math id="M14">$ \{\cdot, \cdot\} $</tex-math></inline-formula></span>表示哈密顿函数<span class="formulaText"><inline-formula><tex-math id="M15">$ H $</tex-math></inline-formula></span>动能部分的代数结构,以及cosymplectic矩阵<span class="formulaText"><inline-formula><tex-math id="M16">$ J $</tex-math></inline-formula></span>,或Lie-Poisson结构<sup>[<xref ref-type="bibr" rid="b19">19</xref>]</sup> ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 系统(2.2)是Kolmogorov描述具有哈密顿函数的不同强迫动力系统,流体动力系统等引入的<sup>[<xref ref-type="bibr" rid="b13">13</xref>]</sup>.在欧拉方程中力(或力矩)<span class="formulaText"><inline-formula><tex-math id="M19">$ \{X, H\} $</tex-math></inline-formula></span>是惯性力(离心力).系统(2.2)是具有耗散力和外力的广义欧拉方程<sup>[<xref ref-type="bibr" rid="b19">19</xref>]</sup>.经变量变换<span class="formulaText"><inline-formula><tex-math id="M21">$ x\mapsto x, y\mapsto y, z\mapsto z-ar- c $</tex-math></inline-formula></span>,系统(2.1)化为 ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 这意味着在Lie-Poisson括号下卡西米尔函数与每个函数可交换<sup>[<xref ref-type="bibr" rid="b19">19</xref>]</sup>.对于Couette-Taylor流系统来说,卡西米尔函数定义为 ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 由(2.3)式和文献[<xref ref-type="bibr" rid="b19">19</xref>],我们有 ...</div> </div> </div> <div id="article_reference_meta_b20"> <div id="article_reference_meta_b20_title" class="title_"></div> <div id="article_reference_meta_b20_citedNumber">1</div> <div id="article_reference_meta_b20_nian">1994</div> <div id="article_reference_meta_b20_jcr"></div> <div id="article_reference_meta_b20_cjcr"></div> <div id="article_reference_meta_b20_articleCitedText"> <div class="sentence">... 其中V是系统相空间的体积.因此,此情形下系统是耗散的,即相空间的体积在流量下以指数形式收缩<sup>[<xref ref-type="bibr" rid="b20">20</xref>]</sup>.哈密顿的能量变化率是 ...</div> </div> </div> <div id="article_reference_meta_b21"> <div id="article_reference_meta_b21_title" class="title_">Thoughts on brackets and dissipation:Old and new</div> <div id="article_reference_meta_b21_citedNumber">1</div> <div id="article_reference_meta_b21_nian">2009</div> <div id="article_reference_meta_b21_jcr"></div> <div id="article_reference_meta_b21_cjcr"></div> <div id="article_reference_meta_b21_articleCitedText"> <div class="sentence">... 我们注意到系统(2.5)的第一项是由哈密顿能量传递的力矩,它似乎与后面两项,即耗散和外力矩没有关系,但从<xref ref-type="fig" rid="Fig11">图 11</xref>中我们发现能量与这两项有关.由于每一类型的力矩是一个耦合的线性或非线性的具有三个分量的矢量,其作用于一个质点上,因此很难研究系统(2.5)的力矩.但是,由于能量是一个标量,所以通过研究能量来发现力矩特征是很容易的,而能量是流体流动的一个重要因素,在接下来的讨论中,我们讨论了能量与这两种力矩的关系.莫里森<sup>[<xref ref-type="bibr" rid="b21">21</xref>]</sup>通过Lyapunov函数将哈密顿动力学的Li-Poisson括号扩展为包括耗散,即 ...</div> </div> </div> <div id="article_reference_meta_b22"> <div id="article_reference_meta_b22_title" class="title_">On the shape and dimension of the Lorenz attractor</div> <div id="article_reference_meta_b22_citedNumber">3</div> <div id="article_reference_meta_b22_nian">1995</div> <div id="article_reference_meta_b22_jcr"></div> <div id="article_reference_meta_b22_cjcr"></div> <div id="article_reference_meta_b22_articleCitedText"> <div class="sentence">... 显然<span class="formulaText"><inline-formula><tex-math id="M70">$ \Xi_0 $</tex-math></inline-formula></span>是<span class="formulaText"><inline-formula><tex-math id="M71">$ {\Bbb R}^3 $</tex-math></inline-formula></span>中的椭球,在<span class="formulaText"><inline-formula><tex-math id="M72">$ \Xi_0 $</tex-math></inline-formula></span>表面上<span class="formulaText"><inline-formula><tex-math id="M73">$ \dot{C} = 0 $</tex-math></inline-formula></span>,所以<span class="formulaText"><inline-formula><tex-math id="M74">$ C(t) $</tex-math></inline-formula></span>的所有极值点均位于<span class="formulaText"><inline-formula><tex-math id="M75">$ \Xi_0 $</tex-math></inline-formula></span>的表面.当系统(2.5)或(5.2)的轨线从<span class="formulaText"><inline-formula><tex-math id="M76">$ \Xi_0 $</tex-math></inline-formula></span>的内部移出时<span class="formulaText"><inline-formula><tex-math id="M77">$ \dot{C}<0 $</tex-math></inline-formula></span>,因此卡西米尔函数下降到<span class="formulaText"><inline-formula><tex-math id="M78">$ \dot{C} = 0 $</tex-math></inline-formula></span>,达到其极小值.当轨线进入<span class="formulaText"><inline-formula><tex-math id="M79">$ \Xi_0 $</tex-math></inline-formula></span>内,有<span class="formulaText"><inline-formula><tex-math id="M80">$ \dot{C}>0 $</tex-math></inline-formula></span>,然后,卡西米尔函数增加直到<span class="formulaText"><inline-formula><tex-math id="M81">$ \dot{C} = 0 $</tex-math></inline-formula></span>达到它的最大值.应该注意的是,三个平衡点均位于<span class="formulaText"><inline-formula><tex-math id="M82">$ \Xi_0 $</tex-math></inline-formula></span>的表面,因为平衡点是通过<span class="formulaText"><inline-formula><tex-math id="M83">$ \dot{X} = 0 $</tex-math></inline-formula></span>求得的,推得<span class="formulaText"><inline-formula><tex-math id="M84">$ \dot{C} = 0 $</tex-math></inline-formula></span><span class="formulaNumber">.</span>受文献[<xref ref-type="bibr" rid="b22">22</xref>]方法的启发,下面我们给出卡西米尔函数和混沌吸引子的边界. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 其中<span class="formulaText"><inline-formula><tex-math id="M124">$ \langle F, L\rangle = g_{ij}\frac{\partial F}{\partial x_i}\frac{\partial L}{\partial x_j} $</tex-math></inline-formula></span>是爱因斯坦符号, <span class="formulaText"><inline-formula><tex-math id="M125">$ L $</tex-math></inline-formula></span>是一个Lyanpunov函数耗散部分, <span class="formulaText"><inline-formula><tex-math id="M126">$ g_{ij} = \frac{1}{2}\varepsilon_{im}^n \varepsilon_{kn}^m $</tex-math></inline-formula></span>是Cartan-Killing指标.运用哈密顿能量与耗散能量交换思想,佩利诺等<sup>[<xref ref-type="bibr" rid="b22">22</xref>]</sup>用<span class="formulaText"><inline-formula><tex-math id="M128">$ L+G $</tex-math></inline-formula></span>替换<span class="formulaText"><inline-formula><tex-math id="M129">$ L $</tex-math></inline-formula></span>,其中<span class="formulaText"><inline-formula><tex-math id="M130">$ G $</tex-math></inline-formula></span>是外力释放的能量.因此,方程(2.5)重写为 ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 由于<span class="formulaText"><inline-formula><tex-math id="M134">$ \{C, K\} $</tex-math></inline-formula></span>和<span class="formulaText"><inline-formula><tex-math id="M135">$ \{C, U\} $</tex-math></inline-formula></span>都为零,卡西米尔函数显然不会与<span class="formulaText"><inline-formula><tex-math id="M136">$ U $</tex-math></inline-formula></span>和<span class="formulaText"><inline-formula><tex-math id="M137">$ K $</tex-math></inline-formula></span>交互(interact with).因此,引入新状态函数<sup>[<xref ref-type="bibr" rid="b22">22</xref>]</sup>. <span class="formulaText"><inline-formula><tex-math id="M139">$ W = \dot{C} = -(2L+G) $</tex-math></inline-formula></span><span class="formulaNumber">.</span>卡西米尔函数是热力学能,因此,卡西米尔变化率为耗散与供给能量之间的交换率.通过类似的方法我们有 ...</div> </div> </div> </div> </div> </div> </div> <div class="cankaowenxian1"></div> <div class="col-xs-3"> <div class="slide" style="top: 367px; display: block;"> <div id="sideToolbar"> <div id="sideCatalog" class="sideCatalogBg"> <div id="sideCatalog-sidebar"> <div class="sideCatalog-sidebar-top"></div> <div class="sideCatalog-sidebar-bottom"></div> </div> <div id="sideCatalog-updown"> <div id="sideCatalog-up" class="sideCatalog-up-disable" title="up"></div> <div id="sideCatalog-down" class="sideCatalog-down-enable" title="down"></div> </div> <div id="sideCatalog-catalog"> <dl style="width: 175px; zoom: 1; top: 0px;" id="outline_dl"> </dl> </div> </div> <i id="sideToolbar-up" style="float:left;"></i> <i id="sideCatalogBtn" style="float:left;"></i> </div> </div> </div> </div> </div> </div> </div> <div class="motaikuang" onclick="guanbiann()"></div> <div class="tupiankuang"> <i class="glyphicon glyphicon-remove-circle guanbi" onclick="guanbiann();"></i> <p class="biaotitupiana"> <span class="yige"></span>/<span class="zongdea"></span> </p> <div class="imgaesa"> <table class="haoshi"> <tr> <td onclick="shang();" class="zuo" > 〈 </td> <td class="zhong"> <img src="" class="tp" onload="xianss2()"> </td> <td onclick="xia();" class="you" > 〉 </td> </tr> </table> </div> <div class="neirong"></div> </div> <div class="biaokuang"> <i class="glyphicon glyphicon-remove-circle guanbi" onclick="guanbiann();"></i> <div class="tuti"></div> <div class="table-responsive liuliu"></div> <div class="biaoshuo"> <p class="mtk-biaoshoen"></p> <p class="mtk-biaoshocn"></p> </div> </div> <div class="qipao-zong" onmouseleave="yichu()"> <div class="qipao-content"> </div> <div class="qipao-jiantou"> <img src="../../../richhtml/1003-3998/richHtml_jats1_1/images/1.png"> </div> </div> </div> </div> </div>  <div class="jiewei" align="center">  <div class="footer"> <div class="banquan"> 版权所有 © 《数学物理学报》杂志社<br> 地址：武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版) <br> E-mail: actams@apm.ac.cn<br> 本系统由北京玛格泰克科技发展有限公司设计开发 </div> </div>   <div class="top_web" id="backtop" style="display:block;"> <span class="glyphicon glyphicon-chevron-up" aria-hidden="true" ></span> </div> <script src="http://121.43.60.238/sxwlxbA/images/1003-3998/js/backtop.js"></script>  </div> </body> <script type="text/javascript" src="../../../richhtml/1003-3998/richHtml_jats1_1/js/wangkan.js"></script> <script src="../../../richhtml/1003-3998/richHtml_jats1_1/js/qrcode.js"></script> <script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script> <script type="text/x-mathjax-config"> MathJax.Hub.Config({ extensions: ["tex2jax.js"], jax: ["input/TeX", "output/HTML-CSS"], tex2jax: {inlineMath: [ ['$','$'], ["\$","\$"] ],displayMath: [ ['$$','$$'], ["\\[","\\]"] ],processEscapes: true}, "HTML-CSS": { availableFonts: ["TeX"] }, TeX: {equationNumbers: {autoNumber: ["none"], useLabelIds: true}}, "HTML-CSS": {linebreaks: {automatic: true}}, SVG: {linebreaks: {automatic: true}} }); $(function() { $(".keyword").each(function() { // key var key = $(this); // value var value = key.text(); // 添加点击事件 $(key).click(function() { // 创建一个form表单 var form = document.createElement("form"); form.method = "post"; form.action = "http://121.43.60.238/sxwlxbA/CN/article/searchArticleResult.do"; form.target = "_blank"; // 将form表单添加到body标签中 document.body.appendChild(form); // 新建表单标签 var formElement = document.createElement("input"); formElement.name = "searchSQL"; formElement.type = "hidden"; formElement.value = "(" + value + "[Keyword])"; form.appendChild(formElement); form.submit(); }); }); }); function sddas(){ $('.kkaqqqq').toggle(); } </script> </html>