1 引言
近年来,自Kermack和McKendrick等人开展工作以来,数学模型在描述传染病行为以及提供有效的控制措施上发挥了重要作用,参见文献[1-3].一些传染病拥有暂时性或永久性免疫力,这些疾病可以通过SIR或SIRS模型来模拟,参见文献[4-6].而其他一些疾病,康复后的个体可能会随着潜在感染而复发,并重新成为感染者,这些疾病可以通过SIRI模型来模拟,其中, S是易感者, I是感染者, R是恢复者.在这种模型中,易感者变成感染者,然后一部分感染者获得暂时的免疫力后移除感染者类,但过后又变得具有传染性.疾病的复发是人类疾病的一个重要特征,例如,人和牛的结核病和疱疹,参见文献[7-9].在文献[7]中, Blower考虑了生殖器疱疹的分区模型,并假设疾病传播的标准发生率和固定的输入率.在文献[9]中, Tudor建立了双线性发生率与总人口数不变的复发性流行病模型.确定性SIRI流行病模型可以表示如下,参见文献[10]
其中,参数
是系统(1.1)的基本再生数,是易感人群中的单个传染性个体二次传播的平均数.系统(1.1)已在文献[10]中被Vargas-De-León研究.作者根据阈值
而且
然而,由于环境噪声的存在,系统(1.1)所涉及的参数不是绝对不变的常数,由于环境的持续波动,它们总是在一些平均值附近波动.因此,有必要考虑流行病模型的随机性.迄今为止,各种类型的随机SIS, SIRS模型都已经被研究,参见文献[11-14],例如,文献[11]的Gray等人建立了具有固定人口规模的随机SIS流行病模型,他们证明了正解的存在唯一性并且还为该疾病在人口中的灭绝性和持久性建立了条件.文献[12]的林等人研究了一类具有免疫接种的随机SIS流行病模型,他们证明了在适当的条件下,解的分布密度在
因此,
事实所驱,我们假定系统(1.2)中的所有系数都是正
当然,系统(1.3)可以简化为以下系统
其中
本文的其余部分按以下方式组织.在第2节,我们介绍了一些需要用到的结果.在第3节,我们证明了在任意正初值下,系统(1.4)正解的存在唯一性.在第4节,我们给疾病的灭绝性建立了充分的条件.在第5节,我们证明了系统(1.4)至少存在一个周期为
2 预备知识
贯穿全文,除非另有说明,令
如果
通常情况下,对任意的
其中初值
如果拉普拉斯微分算子作用于
其中
接下来,我们将给出关于周期马尔可夫过程存在性的一些辅助结果,参见文献[23].
定义2.1 如果对于任意的有限序列
注2.1 在文献[23]中,已经给出当且仅当它的转移概率函数的周期为
时,马尔可夫过程
考虑以下方程
引理2.1 假设方程(2.2)的系数在
其中,
且在某些紧集外
其中,
那么,方程(2.2)的解是一个
注2.2 根据引理
3 正解的存在唯一性
为了研究流行病模型的动力学行为,首先考虑该模型的解是否为全局正解.我们在下面的工作中对全局正解的存在唯一性给出了证明,这也是研究模型(1.3)长期行为的前提.
定理3.1 对任意初值
证 由于系统(1.3)的系数是局部Lipschitz连续的,因此,对任意的初值
贯穿全文,我们令
因此,存在整数
定义
因为对任意的
令
其中
这里
从0到
所以
当
通过不等式(3.3),计算可得
其中
与假设矛盾,所以必然有
注3.1 由定理3.1容易看出
我们得到,如果
那么
因此,区域
是系统(1.3)的正不变集.
4 灭绝性
本节中,通过利用Lyapunov函数方法,我们建立了该疾病绝灭的充分条件.我们将研究无病平衡点
定理4.1 对任意初值
证 由系统(1.4),可得
首先,定义
然后利用Ito公式可得
定义
结合Ito公式,可得
定义下列Lyapunov函数
通过(4.1)和(4.2)式,可得
其中,
这就意味着如果
5 非平凡正周期解的存在性
本节我们将研究系统(1.4)中非平凡正
定理5.1 假设
证 在以下研究中,为了方便起见,我们分别将
定义
其中
其中
通过Ito公式,我们得到
定义
然后结合(5.1)和(5.3)式,可得
同样,我们得到
根据(5.4)和(5.5)式,可得
应用Ito公式,我们得到
且
所以,结合(5.6), (5.7)和(5.8)式,有
现在,我们可以构造一个紧集
其中,
其中
显然,
情形1 如果
通过(5.2)式,可得当
情形2 如果
其中
由(5.9)式可得,对任意的
情形3 如果
由(5.10)式可得:在
显而易见,由(5.11), (5.12)和(5.14)式,我们可以发现,给定一个充分小的
因此,引理2.1中的(2.4)式满足.由引理2.1,我们可以得到系统
注5.1 定理
6 数值模拟
本节,我们将介绍两个例子和一些数值模拟来说明我们的理论结果.
通过用文献[24]里Higham等人的理论方法,我们得到了系统
其中
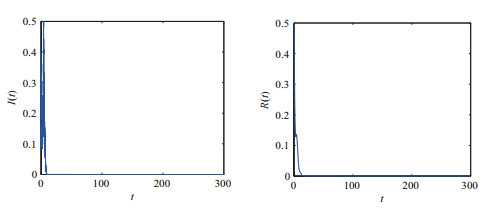
例6.1 假设系统
图 1
图 1
Simulation of paths of
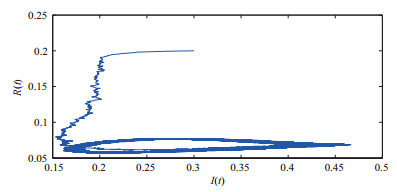
例6.2 假设系统
图 2
图 2
Simulation of paths of
7 总结
本文讨论随机非自治SIRI传染病模型的动力学问题.通过构造一个合适的Lyapunov函数,我们建立了系统(1.4)的非平凡正
当然,还有许多问题值得进一步研究.一方面,我们可以提出一些更现实但更复杂的模型,例如考虑脉冲扰动对系统(1.4)的影响;另一方面,我们模型的一个主要缺点是假设人口的自然死亡率相等,这对于本文的研究是非常必要的.然而,这种假设对系统动力学的影响仍未得到解决.我们把这些问题留待将来研究.
参考文献
Contributions to the mathematical theory of epidemics-I
Analysis of rabies in China:transmission dynamics and control
DOI:10.1371/journal.pone.0020891 [本文引用: 1]
Global stability of an SIR epidemic model with information dependent vaccination
Lyapunov functions and global stability for SIR, SIRS, and SIS epidemiological models
DOI:10.1016/S0893-9659(02)00069-1
Lyapunov functions and global stability for SIR and SIRS epidemiological models with nonlinear transmission
A deterministic model for herpes infections in human and animal populations
On the global stability of infectious disease models with relapse
A stochastic differential equation SIS epidemic model
DOI:10.1137/10081856X [本文引用: 3]
Stationary distribution of a stochastic SIS epidemic model with vaccination
DOI:10.1016/j.physa.2013.10.006 [本文引用: 1]
Global analysis of a deterministic and stochastic nonlinear SIRS epidemic model
Necessary and sufficient condition for extinction and persistence of SIRS system with random perturbation
Existence of two periodic solutions for a non-autonomous SIR epidemic model
DOI:10.1016/j.apm.2010.07.002 [本文引用: 1]
Existence of multiple periodic solutions for an SIR model with seasonality
Existence of a nontrivial periodic solution in an age-structured SIR epidemic model with time periodic coefficients
Periodic traveling waves in SIRS endemic models
Nontrivial periodic solution of a stochastic epidemic model with seasonal variation
The threshold of a non-autonomous SIRS epidemic model with stochastic perturbations
Nontrivial periodic solution of a stochastic non-autonomous SISV epidemic model
DOI:10.1016/j.physa.2016.06.041 [本文引用: 1]
An algorithmic introduction to numerical simulation of stochastic differential equations
DOI:10.1137/S0036144500378302 [本文引用: 1]