当前学术界对Bose-Einstein凝聚(BEC)理论十分关注^[1-4].在光晶格费米(Fermi)气体凝聚体特性有较多的研究.例如波的演化,量子相变,超流与绝缘,用共振技巧来控制光晶格,费米气体光晶格超导性的微观现象和BEC间过渡的隧穿性态,相平面分析和周期性调制研究,超导电性现象等等^[2-18]. Landau-Zener隧穿费米凝聚体量子现象是系统相邻能级间量子的作用^[14].近来,一些学者用动力学解析理论来讨论了费米气体的光晶格模型.作者等也用解析方法研究了一些非线性物理模型^[22-34].本文是用广义变分理论和方法来得到费米气体光晶格模型渐近解的表示式.

费米气体光晶格当凝聚的钠原子光晶格尺度充分小,温度足够低时,从BCS到unitarity渡越过程的动力学现象可用如下薛定谔方程描述^[15-16]

(2.1) $ \begin{align} {\rm i}\hbar\frac{\partial \phi}{\partial t} = -\frac{1}{2M}((\hbar\frac{\partial}{\partial x} -{\rm i}Ma_{l})^{2}\phi+V_{0}\cos(2k_{L}x)\phi+\mu\phi, \end{align} $

其中$ x $是空间变量, $ t $是时间变量, $ \phi $是凝聚体的波函数, $ V_{0} $为光晶格强度, $ \mu $为光晶格体系的化学势, $ M = 2m\ (m $为单个原子的质量), $ k_{L} = \frac{2}{\lambda}\ (\lambda = 1064nm) $为激光的波数, $ Ma_{l} $表示在光晶格中的惯性力.设

$ \widetilde{t} = \frac{4\hbar K^{2}_{L}t}{M}, \ \ \widetilde{x}-2k_{L}x, \ \ \widetilde{\phi} = \frac{\phi}{\sqrt{n_{0}}}, \ \ \widetilde{\alpha} = \frac{M^{2}a_{l}}{8\hbar K^{2}_{L}}, \ \ \widetilde{v} = \frac{mV_{0}}{4\hbar K^{2}_{L}}, $

上式中$ n_{0} = 3\times10^{21}m^{-3} $为Na原子的平均粒子数密度, $ \mu $为超流费米气体从分子BCS渡越到unitarity的过程中化学势^[17]

$ \mu(n, a_{f}) = \frac{2\hbar}{M}(6\pi^{2}n)^{2/3}\widetilde{g}((2n)^{1/3})a_{f}), $

其中$ a_{f} $为散射长度, $ \widetilde{g}(\widetilde{x}) = 1+\delta\widetilde{x}/(1-\kappa\widetilde{x}) $, $ \kappa = \delta/0.56 $, $ \delta = 4\pi/(3\pi^{2})^{2/3} $.而当$ \widetilde{x} > 1 $时系统处于BCS区,当$ \widetilde{x} < 1 $时系统处于unitarity区.

再设$ \overline{\phi} = \xi_{1}\exp({\rm i}(\theta_{1}+\widetilde{x}/2)) +\xi_{2}\exp({\rm i}(\theta_{2}+\widetilde{x}/2)) $,将其以及BCS区和unitarity区的化学势分别代入(2.1)式,便得到布局数差$ s = \xi^{2}_{2}-\xi^{1}_{2} $和相位差$ \theta = \theta_{2}-\theta_{1} $满足典型的光晶格系统^{[14, 18]}

(2.2) $ \begin{align} \frac{{\rm d}s}{{\rm d}\widetilde{t}} = -\widetilde{v}\sqrt{1-s^{2}}\sin\theta, \end{align} $

(2.3) $ \begin{align} \frac{{\rm d}\theta}{{\rm d}\widetilde{t}} = \frac{\widetilde{v}s}{\sqrt{1-s^{2}}}\cos\theta +\frac{d_{1}}{4k^{2}_{L}}s+\frac{d_{2}}{16k^{2}_{L}}s(1-s^{2}), \end{align} $

这里$ d_{i}\ (i = 1, 2) $为常数.由(2.2)式, $ {\rm d}\widetilde{t} = -{\rm d}s/(\widetilde{v}\sqrt{1-s^{2}}\sin\theta) $,将它代入(2.3)式,光晶格系统满足如下微分方程

(2.4) $ \begin{align} \frac{{\rm d}\cos\theta}{{\rm d}s} = \frac{s}{1-s^{2}}\cos\theta+\frac{1}{\widetilde{v}} (\frac{d_{1}}{4k^{2}_{L}})\frac{s}{\sqrt{1-s^{2}}}+ \frac{d_{2}}{16k^{2}_{L}}s\sqrt{1-s^{2}}). \end{align} $

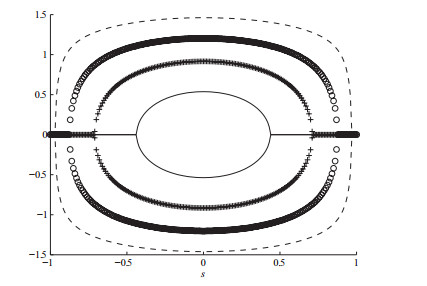
由(2.4)式,便得到费米气体典型光晶格系统的轨线方程

(2.5) $ \begin{align} \cos\theta = C(1-s^{2})^{-1/2} -\frac{1}{64\widetilde{v}k^{2}_{L}}(8d_{1}(1-s^{2})+d_{2}(1-s^{2})^{2}), \end{align} $

(2.5)式中$ C $为任意常数.取不同的常数$ C $时在相平面上有不同的闭轨线曲线.

取无量纲参数$ d_{1} = d_{2} = \widetilde{v} = k_{L} = 1 $,当常数分别取$ C = 1.00, \ 0.75, \ 0.50 $和$ 0.25 $时,在相平面$ o = s\theta\ (-1\leq s\leq 1) $上分别用实线, $ "+" $线, $ "\circ " $线和虚线表示的闭轨线曲线如图 1所示.

在(2.4)式中,作变量变换

(3.1) $ \begin{align} s = \pm(1-\exp(-2r))^{1/2}, \ \ Z = \cos\theta, \ \ r\in[0, \infty). \end{align} $

费米气体典型光晶格系统可用如下参数方程表示

(3.2) $ \begin{align} \frac{{\rm d}s}{{\rm d}r} = \pm\frac{\exp(-2r)}{(1-\exp(-2r))^{1/2}}, \end{align} $

(3.3) $ \begin{align} \frac{{\rm d}Z}{{\rm d}r} = Z+\frac{1}{\widetilde{v}}\bigg(\frac{d_{1}}{4k^{2}_{L}}+ \frac{d_{2}}{16k^{2}_{L}}\bigg)\exp(-r). \end{align} $

这时费米气体典型光晶格系统的轨线参数方程是

(3.4) $ \begin{align} \overline{s}(r) = \pm(1-\exp(-2r))^{1/2}, \end{align} $

(3.5) $ \begin{align} \overline{Z}(r) = \cos\theta = \bigg[C\pm\frac{1}{64\widetilde{v}k^{2}_{L}}(8d_{1}+d_{2}\exp(-2r))\bigg]\exp(-2r), \end{align} $

其中$ C $为任意函数.

由典型光晶格轨线方程参数形式(3.4)和(3.5),我们进一步研究如下费米气体扰动机制光晶格参数形式的系统

(3.6) $ \begin{align} \frac{{\rm d}s}{{\rm d}r} = \pm\frac{\exp(-2r)}{(1-\exp(-2r))^{1/2}}+f(r, s(r), Z(r)), \end{align} $

(3.7) $ \begin{align} \frac{{\rm d}Z}{{\rm d}r} = Z+\frac{1}{\widetilde{v}}\bigg(\frac{d_{1}}{4k^{2}_{L}} +\frac{d_{2}}{16K^{2}_{L}}\bigg)\exp(-r) +g(r, s(r), Z(r)), \end{align} $

其中$ f(r, s(r), Z(r)), g(r, s(r), Z(r)) $为系统的扰动项,设它们是关于其变量为充分光滑的有界函数.

由于费米气体是在光晶格具有扰动机制下的情形.此时一般不能得到轨线的初等函数形式精确解的解析表达式.为此,我们需用渐近表达式去逼近它,下面是用改进的广义变分迭代方法求得轨线的渐近表示式.

引入一组泛函$ F_{i}(s, \theta)\ (i = 1, 2) $

(3.8) $ \begin{align} F_{1}(s, Z) = s-\int^{r}_{0}\lambda_{1}(\tau) \bigg[\frac{{\rm d}s}{{\rm d}\tau}\mp\frac{\exp(-2r)}{(1-\exp(-2\tau))^{1/2}} -\overline{f}(\tau, s, Z) \bigg]{\rm d}\tau, \end{align} $

(3.9) $ \begin{align} F_{2}(s, Z) = Z-\int^{r}_{0}\lambda_{2}(\tau) \bigg[\frac{{\rm d}Z}{{\rm d}\tau}-Z-\frac{1}{\widetilde{v}} \bigg(\frac{d_{1}}{4k^{2}_{L}} +\frac{d_{2}}{16K^{2}_{L}}\bigg)\exp(-r) -\overline{g}(r, s, Z)\bigg]{\rm d}\tau, \end{align} $

其中$ \overline{f}, \overline{g} $分别为$ f, g $的限制变量^[19-21], $ \lambda_{i}\ (i = 1, 2) $为Lagrange乘子.

计算泛函(3.8)和(3.9)的变分$ \delta F_{i}\ (i = 1, 2) $如下

$ \delta F_{1} = \delta s-\lambda_{1}|_{\tau = 0}\delta s+\int^{r}_{0}\bigg[\frac{{\rm d}\lambda_{1}}{{\rm d}\tau}\delta s\bigg]{\rm d}\tau, $

$ \delta F_{2} = \delta Z-\lambda_{2}|_{\tau = 0}\delta Z +\int^{r}_{0} \bigg[\bigg(\frac{{\rm d}\lambda_{2}}{{\rm d}\tau}-1\bigg)\delta Z\bigg]{\rm d}\tau, $

由变分的极值原理,令泛函$ F_{i}\ (i = 1, 2) $的变分$ \delta F_{i}\ (i = 1, 2) $等于零,即$ \delta F_{i} = 0 $.这时Lagrange乘子满足

(3.10) $ \begin{align} \frac{{\rm d}\lambda_{1}}{{\rm d}\tau} = 0, \ \ \lambda_{1}(0) = 1, \end{align} $

(3.11) $ \begin{align} \frac{{\rm d}\lambda_{2}}{{\rm d}\tau}-1 = 0, \ \ \lambda_{2}(0) = 1. \end{align} $

显然,问题(3.10)和(3.11)的解分别为

(3.12) $ \begin{align} \lambda_{1}(\tau) = 1, \ \ \lambda_{2}(\tau) = \tau+1. \end{align} $

考虑到由(3.8)式和(3.9)式决定的泛函$ F_{i}(s, \psi)\ (i = 1, 2) $和关系式(3.12),现构造如下广义变分迭代式

(3.13) $ \begin{align} s_{n+1}(r) = s_{n}(r)- \int^{r}_{0}\bigg[\frac{{\rm d}s_{n}}{{\rm d}\tau}\mp\frac{\exp(-2r)} {(1-\exp(-2\tau))^{1/2}} -f(\tau, s_{n}(x), Z_{n}(\tau))\bigg]{\rm d}\tau, \ \ n = 0, 1, \cdots, \end{align} $

(3.14) $ \begin{align} \begin{array}[b]{rl} Z_{n+1}(r) = & Z_{n}(r)-\int^{r}_{0}(\tau+1) \bigg[\frac{{\rm d}Z_{n}}{{\rm d}\tau}-Z_{n}(\tau)-\frac{1}{\widetilde{v}} \bigg(\frac{d_{1}}{4k^{2}_{L}} +\frac{d_{2}}{16K^{2}_{L}}\bigg)\exp(-r) \\ &-g(\tau, s_{n}(r), Z_{n}(r))\bigg]{\rm d}\tau, \ \ n = 0, 1, \cdots, \end{array} \end{align} $

其中$ s_{0}(\tau), Z_{0}(\tau) $为初始迭代.

选取初始迭代$ s_{0}(\tau), Z_{0}(\tau) $分别为费米气体典型光晶格系统轨线的参数方程的解(2.2)–(2.3),即

(3.15) $ \begin{align} s_{0}(r) = \pm(1-\exp(-2r))^{1/2}, \end{align} $

(3.16) $ \begin{align} Z_{0}(r) = \cos\theta = \bigg[C\pm\frac{1}{64\widetilde{v}k^{2}_{1}}(8d_{1}+d_{2}\exp(-2r))\bigg]\exp(-2r). \end{align} $

于是由(3.15)式, (3.16)式及迭代关系式(3.13)和(3.14),当$ n = 1 $时,有一次迭代渐近解

(3.17) $ \begin{align} s_{1}(r) = s_{0}(r)+\int^{r}_{0}f(\tau, s_{0}(\tau), Z_{0}(\tau)){\rm d}\tau, \end{align} $

(3.18) $ \begin{align} Z_{1}(r) = Z_{0}(\tau)+\int^{r}_{0}(\tau+1)g(\tau, s_{0}(\tau), Z_{0}(\tau)){\rm d}\tau, \end{align} $

其中$ s_{0}, Z_{0} $分别由(3.15)式, (3.16)式表示.

当$ n = 2 $时,有二次迭代渐近解

$ s_{2}(r) = s_{1}(r)- \int^{r}_{0}\bigg[\frac{{\rm d}s_{1}}{{\rm d}\tau}\mp\frac{\exp(-2r)} {(1-\exp(-2\tau))^{1/2}} -f(\tau, s_{1}(\tau), Z_{1}(\tau))\bigg]{\rm d}\tau, $

$ Z_{2}(r) = Z_{1}(r)-\int^{r}_{0}(\tau+1) \bigg[\frac{{\rm d}Z_{1}}{{\rm d}\tau}-Z_{1}-\frac{1}{\widetilde{v}} \bigg(\frac{d_{1}}{4k^{2}_{L}} +\frac{d_{2}}{16K^{2}_{L}}\bigg)\exp(-r) -g(\tau, s_{1}(\tau), Z_{1}(\tau))\bigg]{\rm d}\tau, $

其中$ s_{1}, Z_{1} $分别由(3.17)式, (3.18)式表示.

利用同样的方法可求出序列$ \{s_{n}(\tau), Z_{n}(\tau)\} $,依次地可得到$ n\ (n = 2, 3, \cdots) $次迭代渐近解.

根据变分理论^[19-21],由上述迭代方法得到的序列$ (\{s_{n}\}, \{Z_{n}\}) $是一致收敛的.设

(3.19) $ \begin{align} s(r) = \lim\limits_{n\rightarrow\infty}s_{n}(r), \ \ Z(r) = \lim\limits_{n\rightarrow\infty}Z_{n}(r). \end{align} $

再由广义变分迭代式(3.13)–(3.14),不难看出由(3.17)式决定的极限函数$ (s(r), Z(r)) $是费米气体广义扰动机制光晶格系统的参数方程(3.6)–(3.7)的精确解.

由变量变换式(3.1): $ Z = \cos\theta, \ (s_{n}(r), \theta_{n}(r)) $就是费米气体广义扰动由机制光晶格轨线系统(3.6)–(3.7)的在坐标系$ o $-$ s\theta $相平面上的一组$ n $次近似的轨线参数形式的渐近解.

为了简单起见,选取无量纲参数: $ d_{1} = d_{2} = k_{L} = \widetilde{v} = 1 $,扰动函数$ f = 0 $, $ g = \alpha S^{2} $$ (\alpha $为常数).这时费米气体光晶格扰动轨线参数方程模型(3.6), (3.7)为

(4.1) $ \begin{align} \frac{{\rm d}s}{{\rm d}r} = \pm\frac{\exp(-2r)}{(1-\exp(-2r))^{1/2}}, \end{align} $

(4.2) $ \begin{align} \frac{{\rm d}Z}{{\rm d}r} = Z+\frac{5}{16}\exp(-r)+\alpha s^{2}(r). \end{align} $

由(3.13)式和(3, 14)式,构造如下广义变分迭代式

(4.3) $ \begin{align} s_{n+1}(r) = s_{n}(r)- \int^{r}_{0} \bigg[\frac{{\rm d}s_{n}}{{\rm d}\tau}\mp\frac{\exp(-2r)}{(1-\exp(-2\tau))^{1/2}}\bigg]{\rm d}\tau, \ \ n = 0, 1, \cdots, \end{align} $

(4.4) $ \begin{align} Z_{n+1}(r) = Z_{n}(r)-\int^{r}_{0}(\tau+1) \bigg[\frac{{\rm d}Z_{n}}{{\rm d}\tau}-Z_{n}-\frac{5}{16}\exp(-r) -\alpha s^{2}_{n}(\tau)\bigg]{\rm d}\tau, \ \ n = 0, 1, \cdots, \end{align} $

其中$ s_{0}, Z_{0} $为初始迭代,它们满足方程

(4.5) $ \begin{align} \frac{{\rm d}s_{0}}{{\rm d}r} = \pm\frac{\exp(-2r)}{(1-\exp(-2r))^{1/2}}, \end{align} $

(4.6) $ \begin{align} \frac{{\rm d}Z_{0}}{{\rm d}r} = Z_{0}+\frac{5}{16}\exp(-r). \end{align} $

由(3.15)式和(3.16)式,参数分方程(4.5)–(4.6)的解为

(4.7) $ \begin{align} s_{0}(r) = \pm(1-\exp(-2r))^{1/2}, \end{align} $

(4.8) $ \begin{align} Z_{0}(r) = \bigg[C\pm\frac{1}{64}(8+\exp(-2r))\bigg]\exp(-2r), \end{align} $

其中$ C $为任意常数.

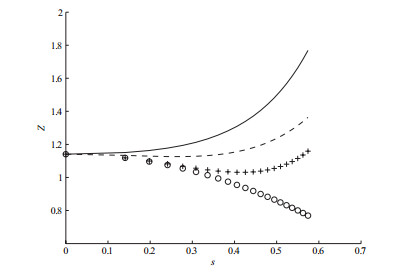
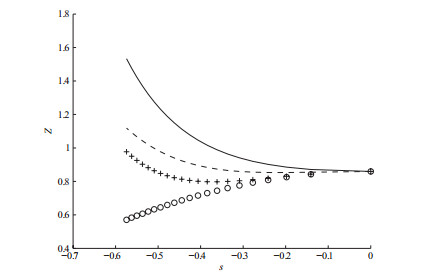
利用迭代式(4.3)–(4.4)和初始迭代(4.7)–(4.8),一次迭代渐近解$ s_{1}(r), Z_{1}(r) $为

(4.9) $ \begin{align} s_{1}(r) = \pm(1-\exp(-2r))^{1/2}, \end{align} $

(4.10) $ \begin{align} Z_{1}(r) = \bigg[C\pm\frac{1}{64}(8+\exp(-2r))\bigg]\exp(-2r) +\frac{\alpha}{2}\bigg[(r^{2}+2r-\frac{2}{3})+(r+\frac{2}{3})\exp(-2r)\bigg]. \end{align} $

再利用迭代式(4.3), (4.4), (4.9)和(4.10).二次迭代渐近解$ s_{2}(r), Z_{2}(r) $为

$ s_{2}(r) = \pm(1-\exp(-2r))^{1/2}, $

$ Z_{2}(r) = Z_{1}(r)-\int^{r}_{0}(\tau+1) \bigg[\frac{{\rm d}Z_{1}}{{\rm d}\tau}-Z_{1}-\frac{5}{16}\exp(-r)-\alpha s^{2}_{1}\bigg]{\rm d}\tau, $

其中$ s_{1}(r), Z_{1}(r) $由(4.9)式, (4.10)式给出.

继续利用迭代式(4.3)–(4.4),可以依次得到任意$ n $次渐近解$ s_{n}(r), Z_{n}(r), \ n = 3.4, \cdots $.

选取$ \alpha = 10, \ C = 1 $,分别取$ s_{0}(r) = +(1-\exp(-2r))^{1/2} $和$ s_{0}(r) = -(1-\exp(-2r))^{1/2} $时,费米气体光晶格扰动轨线参数方程模型(4.1)–(4.2),在相平面o-sZ上的部分轨线分别如图 2, 图 3所示,其中精确解$ Z(s) $用实线表示,对应初始,一次,二次变分迭代轨线的渐近解$ Z_{0}(s) $, $ Z_{1}(s) $, $ Z_{2}(s) $分别用$ " \circ " $线, $ "+" $线和虚线表示.

由变分法的极值原理^[19-21]和图 2, 图 3可以看出,用本文的变分迭代方法得到的各次渐近解逐渐地逼近模型的精确解.

费米气体光晶格系统是较复杂的机制.我们需要把它归化为基本模式且用渐近方法来求解它.利用泛函分析变分迭代方法是一个有效而简单的途径.

因为得到的费米气体光晶格扰动模型的轨线函数是一个解析表示式,故还可对其进行解析的运算,进一步得到相关物理量的性态.