1 引言
近年来,国内外学者通过研究病菌群体感应机理建立相关模型,并对模型进行动力学分析.例如, Müller等人[7]为描述群体感应现象,建立了一类细菌单细胞内AHL产生路径的连续型常微分方程(ODE)模型,刻画了细胞内AHL监管网络体系结构,讨论了模型的动力学性质. 2011年Hooshangi等人[8]针对群体感应发生过程中酶、AHL等物质浓度变化建立了一类连续型ODE模型,数值实验发现细胞内物质合成受AHL浓度的影响.之后, Barbarossa等人[9]针对恶臭假单胞菌种群群体感应现象,建立了一类具有正反馈调节和时滞的负反馈调节的连续型时滞微分方程(DDE)模型,研究了在群体感应作用下, AHL与其分解酶之间的相互作用关系,并对模型进行动力学分析和数值模拟.
基于文献[9],本文拟考虑群体感应发生过程的非连续性的特点,建立一类群体感应机理对AHL浓度调节的非连续ODE模型,讨论模型各类平衡点的存在性、稳定性及其在不连续分界面上的动力学性态.
2 模型的建立
文献[9]中分别记
显然模型(2.1)未考虑群体感应现象何时发生.本文忽略时滞作用,假设群体感应现象发生的非连续性,研究在连续培养基中AHL与其分解酶浓度之间的关系.为此,假设
其中
当
当
在二维空间定义函数
其中
令
3 平衡点的存在性与稳定性
首先研究模型(2.3)和(2.4)平衡点的存在性及稳定性.
3.1 系统(2.3)的动力学性质
为了讨论方便,引入如下符号
令系统(2.3)右端等于零,则其平衡点满足如下代数方程组
定理3.1 系统(2.3)存在唯一的局部渐近稳定的平衡点
证 系统(2.3)在点
其特征根
定理3.2 系统(2.3)在
证 显然
可知系统(2.3)不产生极限环.
结合定理3.1和3.2,有如下结论.
定理3.3 系统(2.3)存在唯一的正平衡点
3.2 系统(2.4)的动力学性质
令系统(2.4)右端等于零,则其平衡点满足如下代数方程组
整理得
其中
定理3.4 当
证 系统(2.4)在点
其特征方程为
整理得
其中
设
事实上,为了证明
将
当
根据Bendixson-Dulac判别法,选取Dulac函数
故系统(2.4)不产生极限环,正平衡点
下面讨论平衡点的真假性.首先比较
整理得
即有
(3.8)式与
定理3.5 (ⅰ)当
(ⅱ)当
(ⅲ)当
3.3 系统(2.5)的动力学性质
本节研究系统(2.5)伪平衡点的存在性、稳定性和极限环的存在性.
3.3.1 系统(2.5)滑线区域的存在性与伪平衡点的局部稳定性
定义在区域
(a)穿越区域:
(b)滑动区域:
(c)逃逸区域:
其中
对于系统(2.5),由计算得穿越区域
在滑动模式区域
在
其中
由此可得
其中
下面讨论伪平衡点的存在性及稳定性.不妨设
当
定理3.6 当
证 若伪平衡点
故系统(2.5)的伪平衡点存在但不稳定.
边界平衡点满足
3.3.3 系统(2.5)极限环的存在性
设
引理3.1 在
证 在
当
显然,当
引理3.2 在
证 在
当
根据系统(2.4)的第二式得
故当
注3.1 对于系统(2.4),根据引理3.2,区域
定理3.7 当
证 首先排除其它类极限环的存在性.
(ⅰ)根据定理3.3和3.4,系统(2.5)不存在全部位于区域
(ⅱ)系统(2.5)不存在与滑线相切或包含一部分滑线的极限环.为排除此类极限环的存在性,只需证明始于切点的轨线不会再次到达滑线.对于系统(2.3),记垂直等倾线为
情形一 当
在滑线
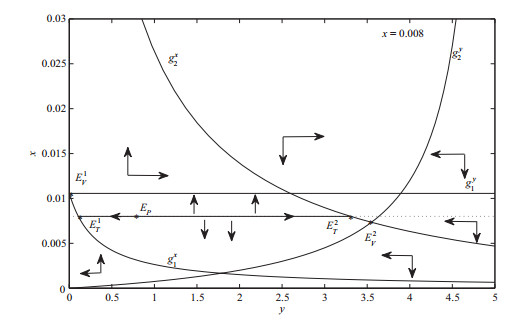
图 1
下面证明从切点
情形二 当
在滑线
情形三 当
(ⅲ)系统(2.5)不存在环绕穿越区域的穿越极限环.
系统(2.5)的穿越区域
接下来,证明系统(2.5)环绕滑动模式区域的穿越极限环的存在性.
(ⅳ)当
当
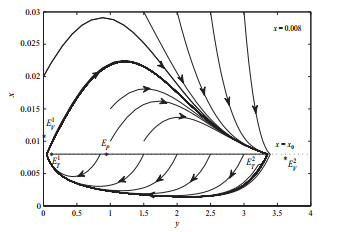
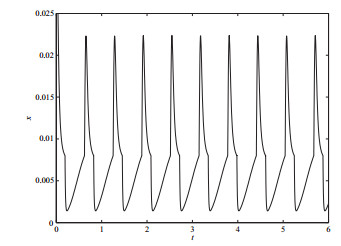
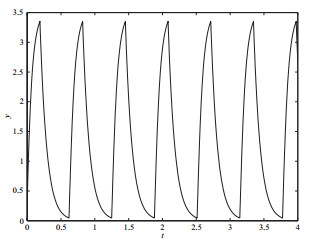
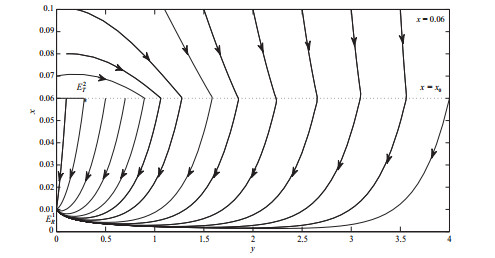
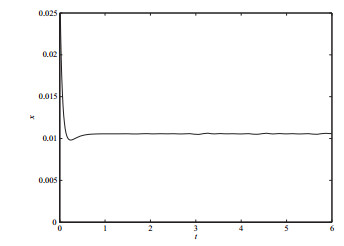
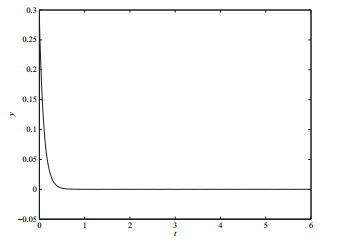
4 数值模拟
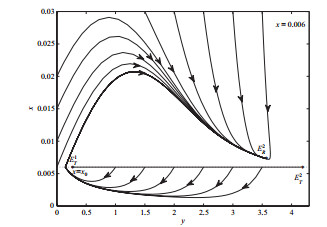
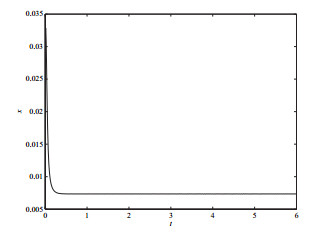
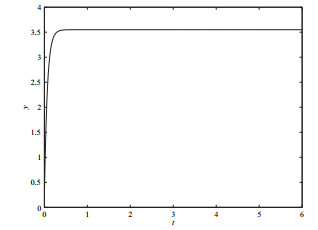
选取分支参数
图 2
图 3
图 4
图 5
图 6
图 7
图 8
图 9
图 10
5 结论
本文建立了一类具有非连续函数的群体感应对AHL浓度调节的数学模型,并讨论了其动力学性质.当
与文献[9]的结果相比较,由于非连续函数的引入,使模型中出现了真、假、伪平衡点及穿越极限环等更加丰富的动力学性态.研究结果表明AHL与其分解酶的浓度在群体感应的调节作用下,最终趋于某一状态.
参考文献
Cellular control of the synthesis and activity of the bacterial luminescent system
How bacteria talk to each Other:regulation of gene expression by quorum sensing
DOI:10.1016/S1369-5274(99)00025-9 [本文引用: 1]
A mathematical model for quorum sensing in pseudomonas aeruginosa
DOI:10.1006/bulm.2000.0205 [本文引用: 1]
Quorum sensing in staphylococcus aureus biofilms
DOI:10.1128/JB.186.6.1838-1850.2004 [本文引用: 1]
Quorum-sensing in gram-negative bacteria
DOI:10.1111/j.1574-6976.2001.tb00583.x
The role of quorum sensing in the in vivo virulence of Pseudomonas aeruginosa
DOI:10.1016/S1286-4579(00)01327-7 [本文引用: 1]
Cell-cell communication by quorum sensing and dimension-reduction
DOI:10.1007/s00285-006-0024-z [本文引用: 1]
LsrR quorum sensing "Switch" is revealed by a bottom-up approach
Mathematical modeling of bacteria communication in continuous cultures
DOI:10.3390/app6050149 [本文引用: 4]