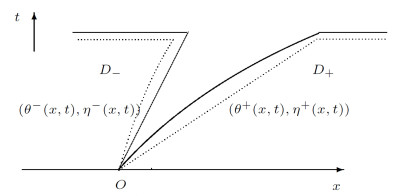
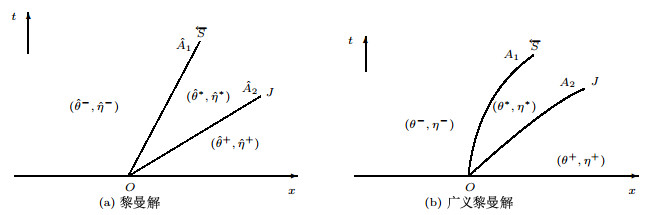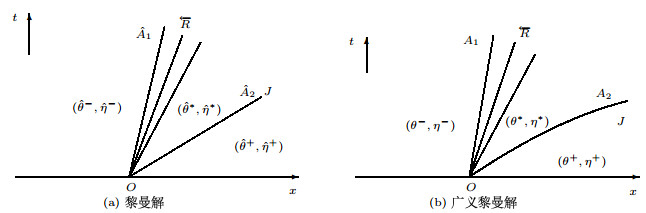1 引言
非线性色谱方程已被化学家和工程学家广泛应用于研究流体相中两种化学成分的分离.在拉格朗日坐标下,非线性色谱方程为
其中
文献[1]中, Ambrosio等人引进变量
方程(1.1)可化为
其中
本文主要目的是研究Delta激波的内部机理和不稳定性.为此,我们研究非线性色谱方程的广义黎曼问题.更精确地,我们考虑方程(1.3)并带有初始条件
其中
这里
广义黎曼问题不仅在守恒律理论中起着重要作用,而且在实际应用当中也非常重要.例如,计算中,误差是不可避免地,误差将会造成原始初始数据的小扰动.
原点附近,广义黎曼问题(1.3)和(1.4)的解是否与对应的黎曼解有类似的结构?本文结果表明:原点附近,如果对应的黎曼解中只有经典初等波,那么黎曼解在初始数据扰动后仍能保持其形式;但如果相应的黎曼解中出现Delta激波,扰动可能会引起解本质的变化.利用以往文献不同的分析方法,我们讨论并且证明广义黎曼问题(1.3)和(1.4)解的结构.从以上结果,我们看到,当初始数据扰动时,黎曼解的不稳定性是由Delta激波引起地,这有助于更好地研究Delta激波的内部机理.
本文结构如下:第二部分介绍一些关于非线性色谱方程(1.3)的预备知识;第三部分给出广义黎曼问题(1.3)和(1.4)的解的构造和证明.
2 预备知识
考虑到本文的完备性,这一部分我们简要回顾有关非线性色谱方程(1.3)的一些基础知识.方程(1.3)的特征值为
因此,除去情况
右特征向量分别为
令
由上可知
对于色谱方程(1.3),沿特征场的黎曼不变量为
考虑带有初始条件(1.6)的黎曼问题(1.3).如果
其中
如果
其中
如果
其中稀疏波
关于黎曼问题(1.3)和(1.6)更详细的研究,请参见文献[19].
3 含有Delta激波的广义黎曼问题
本节中,在
在
区域
接下来,我们求解广义黎曼问题(1.3)和(1.4)在特征线
图 3.1
情况Ⅰ
我们希望广义黎曼问题(1.3)和(1.4)存在局部唯一解,并且该解与相关的黎曼问题(1.3)和(1.6)的解结构相似,即广义黎曼解有如图 3.2(b)所示的结构.这里
沿着接触间断曲线
这里
它由边界条件(3.5)和(3.7)唯一确定.广义黎曼问题(1.3)和(1.4)在区域
图 3.2
由于
定义3.1 对任意
和
为求解上述自由边界问题的最小特征数,我们引进变换
由此,边界条件(3.5)和(3.7)可以改写为
和
根据(3.10)和(3.11)式,我们求出自由边界问题的特征矩阵
引理3.1 假设(3.1)式成立.如果边界条件(3.4)-(3.7)满足以下条件
(Ⅰ.1)
(Ⅰ.2)
(Ⅰ.3)
(Ⅰ.4)
(Ⅰ.5)
那么自由边值问题(1.3)和(3.4)-(3.7)局部时间范围内存在唯一解.
接下来,我们需要验证边界条件(3.4)-(3.7)满足上述五个条件.由于
结合(2.1)和(3.4)式,我们证明了条件(Ⅰ.1)成立.条件(Ⅰ.2)-(Ⅰ.4)的证明非常直接,证明过程省略.进一步地,简单的计算表明
从而,我们证明了该情况下广义黎曼问题(1.3)和(1.4)在原点附近存在唯一的局部解,解如图 3.2(b)所示.对比广义黎曼解和相关的黎曼解,我们得到如下结论:原点附近,黎曼问题(1.3)的解关于黎曼初始值的
情况Ⅱ
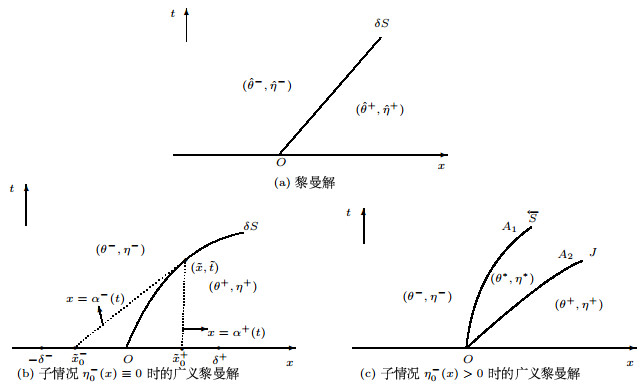
定义3.2 函数对
其中
这里对所有的测试函数
图 3.3
局部时间
下文无特别注释,我们记
及初始条件
我们可以证明Delta激波解(3.16)在
即如以下引理.
引理3.2 假设(3.1)式成立, Delta激波解(3.16)分布意义上满足初始值问题(1.3)和(1.4).
证 由定义3.3,令
利用上式, Delta激波解(3.16)能够改写成如下形式
接下来我们证明(3.20)式满足表达式3.14)和(3.15).
对任意测试函数
由于
类似地,由于
结合上面两式,最后得到
再利用(3.17)式,我们有
上式表明(3.14)成立.
将表达式(3.20)代入方程(3.15)的左边,类似上面的讨论有
同样由于(3.17)式,我们有
因此(3.15)式成立.综上讨论我们证明了局部时间范围内方程(3.16)分布意义上满足初始值问题(1.3)和(1.4).
为保证解的唯一性, Delta激波解在间断线上应满足熵条件,即间断线两侧的四条特征线都是非出地.下面我们给出一个非常重要的定义.
定义3.3 如果间断线上
成立,激波解(3.16)称为在
下面我们需要检验熵条件(3.21)在间断线
此外,当时间
和
根据Rankine-Hugoniot条件,再结合(3.23)和(3.24)式,我们求出了Delta激波曲线
最后,曲线
对比上述不等式和熵条件(3.21), Delta激波解(3.16)满足(3.21)式当且仅当表达式(3.26)中的等号成立.根据不等式(3.26),我们分如下两种子情况进行讨论:
引理3.3 假设(3.1)式成立.当
证 将
这说明熵条件(3.21)在曲线
考虑第二种子情况,即假设
不等式(3.27)说明熵条件(3.21)在曲线
该子情况的自由边界问题的讨论与情况Ⅰ非常类似,我们需要验证它满足引理3.1中的五个条件.由于
这里
我们有
这里
引理3.4 假设(3.1)式成立.当
情况Ⅲ
对于广义黎曼问题(1.3)和(1.4),我们猜测它的解与相关的黎曼解有类似的结构,如图 3.4(b).这里
其中上式右边是关于时间
它的表达形式非常简单.
引理3.5 假设(3.1)式成立.如果边界条件(3.6), (3.7), (3.30)和(3.31)满足下面条件
(Ⅲ.1)
(Ⅲ.2)
(Ⅲ.3)
(Ⅲ.4)
(Ⅲ.5)
那么带有上述边界条件的自由边界值问题(1.3)存在局部(时间)唯一解.
我们需要检验边界条件(3.6), (3.7), (3.30)和(3.31)是否满足引理3.5.直接计算,我们可以验证条件(Ⅲ.1)-(Ⅲ.4)成立.自由边界问题对应的最小特征数
图 3.4
综上情况Ⅰ-Ⅲ,我们完成了广义黎曼问题(1.3)和(1.4)的讨论,并将主要结果总结如下.
定理3.1 假设(3.1)成立.如果时间
参考文献
Some new well-posedness results for continuity and transport equations, and applications to the chromatography system
DOI:10.1137/090754686 [本文引用: 1]
Uniqueness of discontinuous ODE and conservation laws
DOI:10.1016/S0362-546X(97)00590-7 [本文引用: 1]
Formation of δ-shocks and vacuum states in the vanishing pressure limit of solutions to the Euler equations for isentropic fluids
DOI:10.1137/S0036141001399350 [本文引用: 1]
Generalized Riemann problem for Euler system Dedicated to Professor Li TaTsien on the Occasion of His 80th Birthday
Delta shock waves in chromatography equations
DOI:10.1016/j.jmaa.2011.04.002
The generalized Riemann problem for the motion of elastic strings
The Two-Dimensional Riemann Problem in Gas Dynamics
Nonclassical composition fronts in nonlinear chromatography:delta-shock
DOI:10.1021/ie9001537 [本文引用: 1]
Experimental evidence of a delta-shock in nonlinear chromatography
DOI:10.1016/j.chroma.2010.01.059 [本文引用: 1]
Delta and singular delta locus for one dimensional systems of conservation laws
The generalized Riemann problem for a scalar nonconvex combustion model-the perturbation on initial binding energy
The Riemann problem admitting δ-and δ'-shocks and vacuum states (the vanishing viscosity approach)
DOI:10.1016/j.jde.2006.08.003 [本文引用: 1]
The Riemann problem for the Chaplygin gas equations with a source term
Formation of delta shocks and vacuum states in the vanishing pressure limit of Riemann solutions to the perturbed Aw-Rascle model
DOI:10.1016/j.jde.2010.09.004 [本文引用: 1]
Delta wave and vacuum state for generalized Chaplygin gas dynamics system as pressure vanishes
DOI:10.1016/j.nonrwa.2014.08.007
The Riemann Problem for the transportation equations in gas dynamics
Delta shock waves for the chromatography equations as self-similar viscosity limits
DOI:10.1090/S0033-569X-2011-01207-3 [本文引用: 2]
Interactions of delta shock waves for the chromatography equations
New developments of delta shock waves and its applications in systems of conservation laws
DOI:10.1016/j.jde.2012.02.015 [本文引用: 3]