1 引言
有借贷利率的风险模型可以表示为下面微分方程的解
其中,
分红问题是保险精算的主要课题之一.经典的障碍分红是指盈余到达某个给定的分红水平
本文结构如下:第二部分是模型介绍,第三部分用分割游程的方法得到了有借贷利率的经典模型的折现Parisian延迟分红的表达式.
2 模型介绍
本文我们研究绝对破产模型(1.1)的Parisian延迟分红问题.令
对于
假设
表示
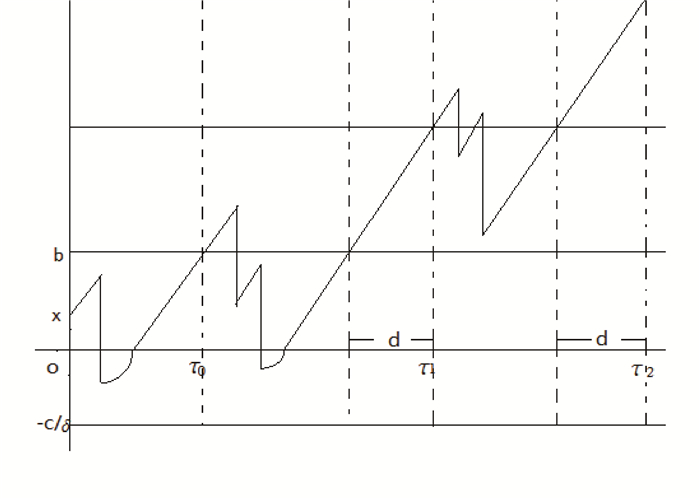
图 1
由以上定义,当
且
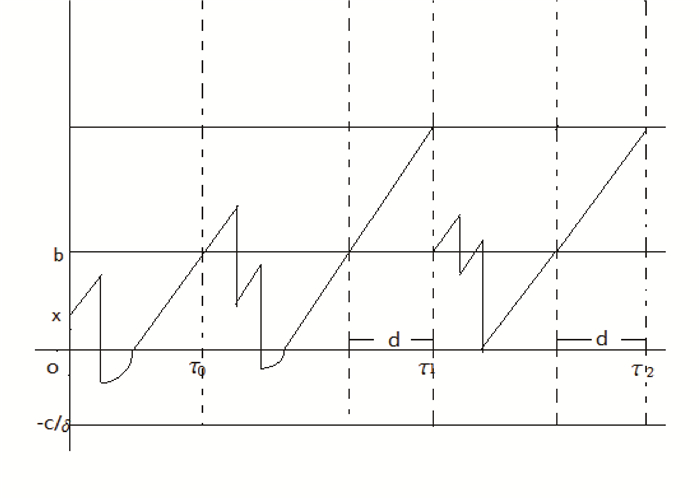
图 2
过程
绝对破产前总分红支出为
其中
为了得到预期结果,我们需要借助以下引理.
引理2.1[8] 令
其中
分别是方程
的两个实根.而
其中,
引理2.2[9] 在索赔量服从参数为
(1)初值为
其中
(2)破产时间的密度函数为
其中
是
引理2.3[3] 在索赔量服从参数为
3 折现期望分红
下面我们给出有借贷利率的经典模型的折现延迟分红.为了方便问题的处理,我们以下所有问题都是在假设了索赔量服从参数为
定理3.1 在Parisian延迟条件下,有借贷的经典风险模型的折现分红为
其中
的根,且
证 设
而
因此
根据模型的定义知,在第一次分红时刻
因此,要计算累积期望分红,只需要得到以下几个结果即可
首先考虑
可得
下面来看
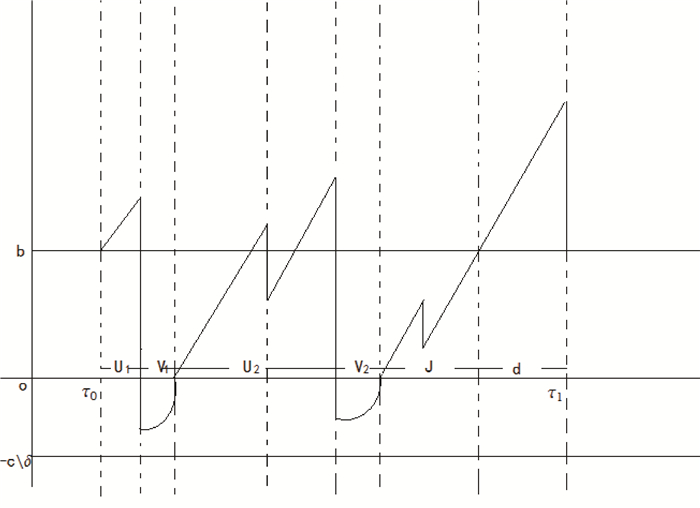
图 3
我们这样研究游程
下面我们来定义
令
首先对于在
由引理2.2得,初值为0的经典盈余过程破产时间的密度函数为
又因为
下面来看
至于
对于0之下的游程
我们用
由于
通过以上的定义,我们可以把
因为
另外,由定义知
由于
因此,当
因此
其中
将(3.13)和(3.15)式分别带入(3.14)式得到
将(3.6), (3.13)和(3.16)式分别代入(3.5)式得到
证毕.
参考文献
Martingales and insurance risk
DOI:10.1080/15326348908807105 [本文引用: 1]
古典风险模型下的绝对破产
DOI:10.3321/j.issn:0254-3079.2005.04.013 [本文引用: 1]
Absolute ruin under classical risk model
DOI:10.3321/j.issn:0254-3079.2005.04.013 [本文引用: 1]
Absolute ruin problems for the risk processes with interest and a constant dividend barrier
On barrier strategy dividends with Parisian implementation delay for classical surplus processes
DOI:10.1016/j.insmatheco.2009.05.013 [本文引用: 4]
Dividend problem with Parisian delay for a spectrally negative Levy risk process
DOI:10.1007/s10957-013-0283-y [本文引用: 1]
复合二项对偶模型中的周期性分红问题
Optimal dividend strategy in compound binomial dual model with bounded dividend rates and periodic dividend payments
Dividend payment in the classical risk model under absolute ruin with debit interest
DOI:10.1002/asmb.722 [本文引用: 1]
On the density and moments of the time of ruin with exponential claims
DOI:10.1017/S0515036100013271 [本文引用: 1]
Piecewise-deterministic Markov proesses:A general class of non-diffusion stochastic models