奇异特征分解算法(POD)是一种高效的数据处理方法,通过高维过程在低维空间的近似来描述高维过程. Kosambi^[1]于1943年首先提出了POD算法的概念.此外, POD方法也被称为Karhunen-Lo$\acute{e}$ve分解. POD方法可用于结构振动、湍流、昆虫和损伤检测近似中的低维描述^[2-6].此外,它还广泛应用于信号分析、图像处理和数据压缩等领域.在POD方法中,数据通常来源于实验或微分系统的离散. “模态函数”被用来提取信息,以便生成低维模拟系统^[7].

在实际应用中,不同的研究人员使用了不同的随机信号.例如, Bienkiewicz^[8-9]等使用全信号来得到相关矩阵(CROM),但更多的研究人员则使用去除均值的信号来得到方差矩阵,很少有人研究其中的原因.文献[10-11]试图分析均值场对POD方法的影响,但这些文献只是给出了一些数值例子,并没有给出理论结果.因此,有必要从理论上对均值场在POD方法中的影响机制进行分析.

该文基于POD理论和矩阵分解,通过引入均值场的相关矩阵,研究了均值场对整个信号和信号波动部分的影响机制.采用数值算例验证了均值场对POD过程的影响.虽然均值场不影响POD算法的分解和重构过程,但由两种不同类型的信号(如选择适当的模态)所获得的参数都深刻受到其影响而差别很大,原因在于所获得的参数反映了原始信号,这两种不同信号不应被混淆.使用全信号时,所得参数受均值场影响而失真,尤其是低阶模态.在实际应用中,信号的均值场和波动部分有时单独被使用,因此在POD过程中,使用去除均值的信号是非常实用的,这可以避免均值场对算法的影响,从而保持原始信号的特性.

为了方便而不失一般性,假设$u(x, t)$为标量或向量场,可通过实验、观测或数值计算得到.将求解区域离散为$(x_i, t_j), i=1, 2, \cdots, m; j=1, 2, \cdots, n$, $u(x, t)$的矩阵形式为

(2.1)$ \begin{equation} U_{m\times n}=\left( \begin{array}{ccccccc} {u}_{11}&{u}_{12} &\cdots& {u}_{1n}\\ {u}_{21}&{u}_{22}&\cdots& {u}_{2n}\\ \cdots&\cdots&\cdots& \cdots\\ {u}_{m1}&{u}_{m2}&\cdots& {u}_{mn} \end{array} \right). \end{equation} $

矩阵$U$的行平均值表示为$\overline{U}$,矩阵$U^0_{m\times n}$为

(2.2) $ \begin{equation} \overline{U}=\frac{1}{n}\bigg(\sum\limits_{j=1}^{n}u_{1j}, \sum\limits_{j=1}^{n}u_{2j}, \cdots, \sum\limits_{j=1}^{n}u_{mj}\bigg)^T=(\bar{u}_1, \bar{u}_2, \cdots, \bar{u}_m)^T, \end{equation} $

(2.3) $\begin{equation} U^0_{m\times n}=\left(\begin{array}{ccccccc}\bar{u}_1& \bar{u}_1 &\cdots& \bar{u}_1\\\bar{u}_2&\bar{u}_2&\cdots& \bar{u}_2\\\cdot&\cdot&\cdot& \cdot\\\bar{u}_m&\bar{u}_m&\cdots& \bar{u}_m\end{array}\right).\end{equation} $

为了区别,记$U$为$U^w$.设$U^f=U^w-U^0$,其中$U^w$和$U^f$分别是全信号和去除均值的信号,其维数都是$m\times n$.令

(2.4)$\begin{equation}R^w=U^w*({U^w})^{T}, \ R^f=U^f*({U^f})^{T}, \ R^0=U^0*({U^0})^{T}, \end{equation}$

其中$R^w$是全信号$U^w$的相关矩阵, $R^f$是去除均值信号$U^f$的方差矩阵, $R^0$是均值场的相关矩阵.令

(2.5)$\begin{equation}R\Phi=\Phi\Lambda, \end{equation}$

其中$\Lambda=diag(\lambda_1, \lambda_2, \cdots, \lambda_m)$是对角矩阵, $\lambda_i$是第$i$个特征值且$\phi_i$是对应于第$i$个特征值的特征向量, $\Phi=(\phi_1, \phi_2, \cdots, \phi_m)$是特征矩阵.很显然矩阵$R$是埃尔米特矩阵,矩阵$\Phi$是正交矩阵,列向量$\{\phi_1, \phi_2, \cdots, \phi_m\}$构成一组线性无关正交基函数,因此,对于任意$t_s$,函数$u(x, t_s)$均可表示为$\phi_1, \phi_2, \cdots, \phi_m$的线性组合

(2.6)$\begin{equation}u(x, t_s)=\sum\limits_{i=1}^{m}\alpha_i(t_s)\phi_i.\end{equation}$

因此

(2.7)$\begin{equation}u(x, t)=\Phi\alpha(t), \end{equation}$

(2.8)$\begin{equation}\alpha(t)=(\alpha_1(t), \alpha_2(t), \cdots, \alpha_m(t))^T.\end{equation}$

到目前为止,很少有文献提到时间系数集合$\{\alpha(t)\}$的性质.在该文中研究了时间系数集合$\{\alpha(t)\}$的基本性质.根据问题的需要,该文中不同地方的$u(x, t)$可能是全信号、去除均值部分的信号或均值场三者之一.

为了分析均值对POD方法的影响,须深入分析POD结果的组成.由$U^f$的定义,有

(3.1)$ \begin{equation} R^w=R^0+R^f, \ R^0=U^0(U^0)^T, \ \lambda^0=\sum\limits_{i=1}^{m}(U^{0T}U^0)_{ii}, \end{equation} $

(3.2)$\begin{equation} \{\alpha^w(t)\}=\Phi^{wT}U^w=\Phi^{wT}(U^0+U^f)=\Phi^{wT}U^0+\Phi^{wT}U^f. \end{equation}$

定理3.1  在奇异特征分解过程中,对于任意原始信号$u(x, t)$,相应的时间系数集合$\{\alpha(t)\}$是正交的.此外,内积$(\alpha_i(t), \alpha_j(t))=\delta_{ij}\lambda_i.$

证  由$\phi_i^{T}$的正交性和矩阵$R$的定义,以及方程(2.6),可得到

(3.3)$\begin{equation}\phi_i^{T}u(x, t)=\phi_i^{T}\sum\limits_{i=1}^{m}\alpha_i(t)\phi_i=\alpha_i(t), \end{equation}$

因而

(3.4)$\begin{equation}\alpha_i(t)=\phi_i^{T}u(x, t), \end{equation}$

(3.5)$\begin{equation}(\alpha_i(t), \alpha_j(t))=\alpha_i(t)\overline{\alpha_j(t)}=\phi_i^{T}u(x, t)u(x, t)^T\phi_j=\phi_i^{T}R\phi_j=\delta_{ij}\lambda_i.\end{equation}$

证毕.

定理3.2  对于任意$t$,随机场$u(x, t)$的能量等于特征值$\lambda_i$的总和.

证  由方程(2.6)以及正交集和$\{\phi_i\}$,有

(3.6)$\begin{equation}u(x_k, t)\overline{u(x_k, t)}=\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{m}\alpha_i(t)\overline{\alpha_j(t)}\phi_{ik}\overline{\phi_{jk}}=\sum\limits_{i=1}^{m}\lambda_i\phi_{ik}^{2}, \end{equation}$

(3.7)$\begin{equation}\sum\limits_{k=1}^{m}u(x_k, t)\overline{u(x_k, t)}=\sum\limits_{k=1}^{m}\sum\limits_{i=1}^{m}\lambda_i\phi_{ik}^{2}=\sum\limits_{k=1}^{m}\lambda_k.\end{equation}$

证毕.

定理3.3  对于任意$t$,随机场$u(x, t)$的能量可分解为去除均值的信号部分与均值场的能量之和.

证  设$\lambda_{1}^w, \lambda_{2}^w, \cdots, \lambda_{m}^w$和$v_{1}^w, v_{2}^w, \cdots, v_{m}^w$分别是相关矩阵$R^w$的特征值与特征向量, $\lambda_{1}^f, \lambda_{2}^f, \cdots, \lambda_{m}^f$和$v_{1}^f, v_{2}^f, \cdots, v_{m}^f$是方差矩阵$R^f$的特征值和特征向量, $\lambda_{1}^0, \lambda_{2}^0, \cdots, \lambda_{m}^0$和$v_{1}^0, v_{2}^0, \cdots, v_{m}^0$是均值相关矩阵$R^0$的特征值与特征向量.

由于

(3.8)$\begin{equation}R^w=R^f+R^0, \end{equation}$

(3.9)$\begin{equation}\sum\limits_{i=1}^m\lambda_i^w=\sum\limits_{i=1}^mR^w_{ii}, \ \sum\limits_{i=1}^m\lambda_{i}^f=\sum\limits_{i=1}^mR_{ii}^f, \ \sum\limits_{i=1}^m\lambda_{i}^0=\sum\limits_{i=1}^mR_{ii}^0, \end{equation}$

因此

(3.10)$\begin{equation}\sum\limits_{i=1}^m\lambda_{i}^w=\sum\limits_{i=1}^m\lambda^{f}_i+\sum\limits_{i=1}^m\lambda^{0}_i.\end{equation}$

所以

(3.11)$\begin{equation}\sum\limits_{k=1}^{m}u^w(x_k, t)\overline{u^w(x_k, t)}=\sum\limits_{k=1}^{m}u^f(x_k, t)\overline{u^f(x_k, t)}+ \sum\limits_{k=1}^{m}\overline{u}_k\overline{\overline{u}_k}.\end{equation}$

证毕.

由定理3.3的结论,可以很容易地建立一个平均值获得任意能量的矩阵.

定理3.4  矩阵$R^w$的秩为$0$或$1$.若矩阵$R^w$的秩为$0$,那么$R^w$等于方差矩阵$R^f$.如果矩阵$R^w$的秩为$1$,则$|rank(R^w)-rank(R^f)| \leq 1.$

证  均值矩阵$R^0$有两种情况.如果矩阵$R^0$是零矩阵,则由方程(3.8)有$R^w=R^f$.

如果$rank(R^0)=1$,由$R^w=R^f+R^0$及秩不等式^[13]:如果矩阵$A, B\in R^{m, n}$,则

$|rank(A)-rank(B)| \leq rank (A+B)\leq rank(A)+rank(B), $

因此

$|rank(R^f)-rank(R^0)| \leq rank (R^f+R^0)=rank (R^w)\leq rank(R^f)+rank(R^0).$

证毕.

由$R^0$的定义,可得以下推论.

推论3.1  矩阵$R^0$的特征值为$\overline{U}^T\overline{U}$,相应的特征向量为$n\overline{U}\cdot\overline{U}^T$.

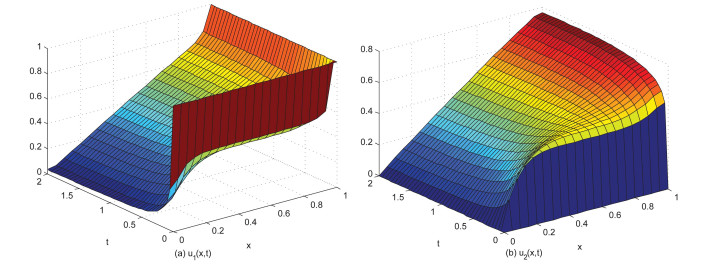
为说明均值对奇异特征分解算法的影响,考虑下面的非线性微分方程初边值问题:求$u(x, t)=[u_1(x, t); u_2(x, t)]^T$使得

(4.1)$\begin{equation} \left\{ \begin{array}{ll} \frac{\partial u_1}{\partial t}=0.024\frac{\partial^2 u_1}{\partial x^2}-F(u_1-u_2), \ &(x, t)\in (0, 1)\times (0, T], \\ \frac{\partial u_2}{\partial t}=0.17\frac{\partial^2 u_2}{\partial x^2}+F(u_1-u_2), \ &(x, t)\in (0, 1)\times (0, T], \\[3mm] u_1(x, 0)=1, \ u_2(x, 0)=0, \ &x\in (0, 1), \\[3mm] \frac{\partial u_1}{\partial x}(0, t)=0, \ u_2(0, t)=0, \ &t\in (0, T], \\[3mm] u_1(1, t)=1, \ \frac{\partial u_2}{\partial x}(1, t)=0, \ &t\in (0, T], \end{array}\right.\end{equation}$

其中$F(x)=e^{5.73x}-e^{-11.46x}, \ T=2.$解$u(x, t)$如图 1所示.

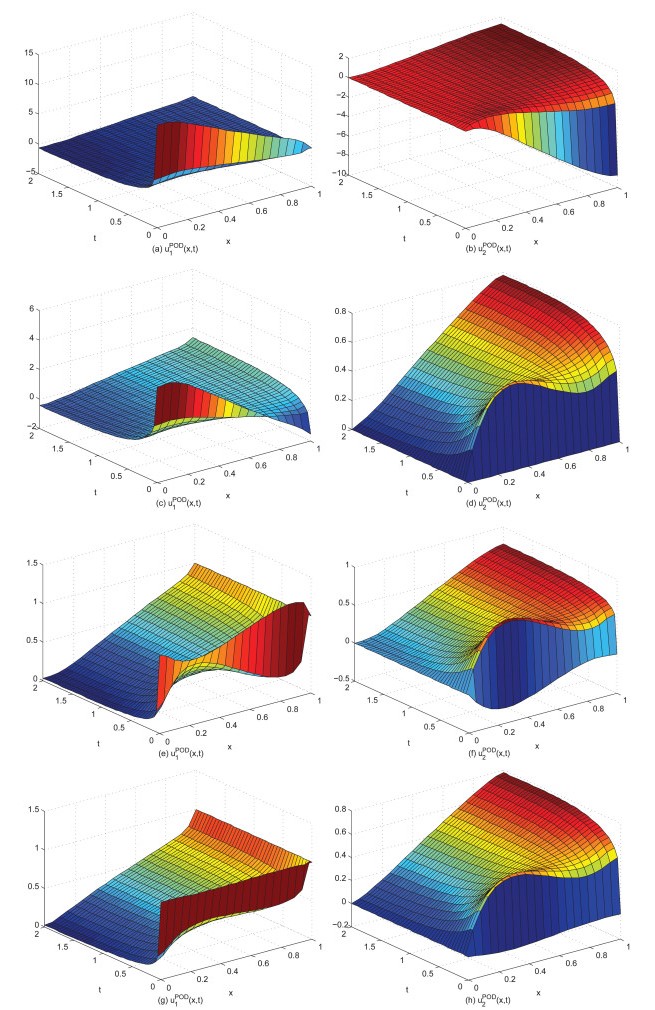
本节中,给出并比较了两种试验方案.方案1:将解函数

$u(x, t)=[u_1(x, t); u_2(x, t)]^T$

作为一个整体函数进行POD分解.方案2:将解分量$u_1(x, t)$和$u_2(x, t)$分别进行POD分解.在两种方案的基础上,全信号和去除均值部分信号分别用来构造相关矩阵$R^w$和方差矩阵$R^f$来分析均值的对POD算法的影响. 表 1中列出了两种方案以及不同相关矩阵的奇异特征值及其所占百分比.结果表明,如果使用全信号,则最大特征值$\lambda_1^w$的所占的百分超过所有能量的96%还多,其所占比例远远大于其余奇异值.如果使用去除均值部分的信号,则最大奇异值$\lambda_1^f$的所占百分比超过所有能量的72%这在整个能量中占有的比率比全信号的最大奇异值所占百分比低,而$R^w$的前四个最大奇异值的总和几乎与$R^f$的前四个奇异值的总和所占比例相同.另外, $R^w$中的奇异值大于$R^f$中相应的奇异值,这是因为在$R^f$中,剔除了均值的影响.

为比较重构解的精确度,只使用第一个空间模态$\phi_1$进行重构解,结果如图 2所示.在图 2中, (a)-(d)是全信号重构解的近似值, (e)-(h)是去除均值部分的信号重构解的近似值. (a)-(b)和(e)-(f)是第一种方案的近似值, (c)-(d)和(g)-(h)是第二种方案的近似值.从图 2中,可以得出以下两个结论.

(1)显然,即使$R^w$中最大奇异特征值所占的百分比远高于$R^f$中最大奇异特征值所占的比例,去除均值部分的信号所得的结果也比全信号的结果好得多.这充分说明在使用POD方法时只使用模态所获取的能量来作为决定空间模态的数目是远远不够的;

(2)如果研究的信号中含有不同频率的组成成分,则不应将研究的信号视为一个整体,将其组成成分单独进行POD分解,重构效果更好.

为了更加具体地分析均值的影响,引入如下几种范数来衡量POD重构解与真解之间的误差. $t=T$时,最大绝对误差,最大相对误差和$L^2$误差定义如下

(4.2)$\begin{equation}||e||^{MAXE}_{\infty}=\max\limits_i|u(x_i, T)-u_{iT}^{POD}|, \end{equation}$

(4.3)$\begin{equation}||e||^{MARE}_{\infty}=\max\limits_i\frac{|u(x_i, T)-u_{iT}^{POD}|}{u(x_i, T)}, \end{equation}$

(4.4)$\begin{equation}||e||_{L^2}^2=\sum\limits_{i=1}^m|u(x_i, T)-u_{iT}^{POD}|^2.\end{equation}$

这些误差如表 2-4所示.从这些表中可以看出,均值主要影响低阶空间模态,尤其是第一阶空间模态,仅用第一阶空间模态来重构解是远远不够的,原因在于均值场会破坏原始信号,所以无论最大奇异特征值能够捕获多少能量都是不够的.此外,任何情况下,都应使用去除均值部分的信号来重构解.

该文主要研究了POD方法中的时间系数集合$\{\alpha(t)\}$的一些基本性质,并从理论上推导了均值对POD方法的影响机制.结论如下.

(1)基于POD方法的理论和矩阵分析,通过引入全信号和去除均值部分信号的相关矩阵,分析了均值对POD方法的影响机制,比较了全信号和去除均值部分信号重构解的结果,推导出这两种信号之间的关系,最后使用一个数值例子来说明这一理论的合理性.首先消除信号的均值部分对整体信号重建的影响,这就是为什么大多数研究人员在实际应用中使用选择去除均值部分信号的原因.

(2)在POD方法中,无论随机场是否包括均值,求得的时间系数集合都是正交的.因此,可以使用不同个数的空间模态来重构原始随机场.如果使用所有空间模态,所得重构解将是真解.

(3)虽然均值场不影响POD过程中的分解和重构,但是否去除均值,所得的奇异特征值、空间模态和主坐标等参数都差别很大,因此,在实际应用中,不该混淆这些系数的物理意义.

(4)仅使用一阶空间模态来重构解是远远不够的,即使最大奇异特征值能捕获任意多的系统能量.