1 引言
近几十年来,复数神经网络得到了深入的研究并取得了广泛的应用.复数神经网络是实数神经网络的扩展,其状态向量,连接权和激活函数均为复值.在许多工程应用中,例如自适应信号处理,通信工程和医学影像,系统的输入和输出以复数形式表示,而复数神经网络由于能够直接处理复数信息,因此非常适合处理这类问题.此外,复数神经网络还可以解决一些实数神经网络无法解决的问题,如文献[1].
对神经网络的动力学行为的研究是神经网络应用的理论基础.在实数神经网络中,激活函数往往被要求是连续函数,甚至要求满足Lipstchiz条件.这样的条件是非常严格的,在实际应用中很多函数是不连续的,无法满足这个条件,因此产生了具有不连续激活函数的神经网络. Forti和Nistri在文献[2]中指出,具有不连续激活函数的神经网络是非常重要的,经常在应用中出现并广泛用于解决许多工程应用中的问题,如冲击机、电力电路、电子电路的开关、线性互补系统等.因此,对于具有不连续激活函数的神经网络动力学性质的研究,也得到了越来越多的关注,见文献[3-9].在文献[3]中,作者研究了一类具有不连续激活函数的时滞神经网络,给出了平衡点的存在唯一性以及全局稳定性的充分条件.在文献[4]中,作者结合Filippov理论, M-矩阵及Lyapnov函数方法研究了具有不连续激活函数的神经网络平衡点的存在唯一性及全局指数稳定性.在文献[5]中,作者研究了具有不连续激活函数的时滞Cohn-Grossberg神经网络,给出了平衡点存在唯一性及全局稳定性的充分条件.在文献[6]中,作者利用Leray-Schauder替换定理,矩阵理论和Lyapunov方法,给出了周期解存在唯一性及全局渐进稳定性的充分条件.在文献[9]中,作者利用微分包含方法研究了一类具有不连续激活函数的离散型神经网络,并给出了神经网络全局渐进稳定性的充分条件.
另一方面,在复数域中,根据刘维尔定理,有界整函数必为常数,因此,在实数神经网络中经常用作激活函数的sigmoid函数就无法作为复数神经网络的激活函数.故在设计复数神经网络中,我们往往选取不连续函数作为激活函数,这样也产生了具有不连续激活函数的复数神经网络.近年来,大批学者对复数神经网络的动力学性质进行了深入的研究,见文献[10-16],但对于具有不连续激活函数的复数神经网络的研究还很欠缺.在文献[17]中,作者研究了具有不连续激活函数的复数神经网络,并给出了平衡点全局渐进稳定以及有限时间收敛的充分条件.鉴于此,本文将在文献[17]的基础上,对具有不连续激活函数的复数神经网络的动力学性质进行进一步的探讨,并给出神经网络周期解指数稳定的充分条件.本文剩余内容结构如下:在第2节中,我们将介绍具有不连续激活函数的复数神经网络模型,复值微分方程的Filippov包含,以及一些相关的预备知识;第3节和第4节中,我们分别对周期解的存在性和全局指数稳定性进行了讨论,给出了周期解全局指数稳定性的充分条件;第5节中,我们给出了一个仿真例子验证结果的有效性;最后在第6节中我们对本文的研究内容进行了总结.
符号说明:在本文中,
2 预备知识
本文中,我们考虑如下的具有不连续激活函数的复数神经网络
其中
假设不连续激活函数
(H
(H
(H
我们首先介绍下述右端不连续的复值微分方程的Filippov微分包含
其中
定义2.1 设
定义2.2 对于复值微分方程(2.2),集值映射
其中,
注2.1 根据实函数绝对连续性的定义,我们可以类似地定义复函数的绝对连续性.假设
那么
注2.2 集值映射
定义2.3 当以下两个条件成立时,向量函数
(1)
(2) 存在可测函数
满足(2.4)的可测函数
下面我们给出与复数神经网络模型(2.1)相关联的初值问题(IVP)解的定义.
定义2.4 与可测函数
注2.3 系统(2.1)的解满足
注2.4 考虑下列微分包含
可以得到,如果
是微分方程(2.1)的一个
定义2.5 设
在本文中,我们选择下列函数作为系统(2.1)中的激活函数
其中
其中
根据(H
其中
根据(H
其中
根据定义2.2,可知系统(2.1)的解
令
则(2.11)式可以重写为
根据注2.4及上述分析,系统(2.1)的
因此,我们可以通过分析问题(2.13)的解来分析系统(2.1)周期解的存在性和全局指数稳定性.
下面,我们介绍证明周期解存在性的Leray-Schauder替换定理以及复合函数求导的计算法则.
引理2.1[6] (Leray-Schauder替换定理) 如果
(1)
(2)
引理2.2[6] 如果
其中
为讨论复数神经网络模型(2.1)的周期解的存在性,我们引入一些记号.令
引理2.3[6]
令
引理2.4[6]
3 周期解的存在性
在这一节中,我们将研究系统(2.1)周期解的存在性.首先,我们考察系统的可行性,即在
定理3.1 如果假设(H
证 根据上一节中(2.12)式的分析,可以得到集值映射
是上半连续的,且集合
从而有
其中
根据(2.12)式,对于不动点
由此可得
因此可知
证毕.
定理3.2 如果假设(H
(H
其中
(H
其中
证 该定理等价于不动点问题
因为
其中
由假设(H
因此可以得到
其中
考虑以下Lyapunov函数
因为
根据引理3,计算
其中
这意味着当
通过
4 周期解的全局指数稳定性
为了证明周期解的全局指数稳定性,我们首先将周期解
其中
其中
定理4.1 如果假设(H
证 选择一个常数
其中
根据引理2.3,我们将
其中
根据(3.8)式可以得到
这就证明了系统(2.1)的周期解的唯一性和全局指数稳定性.
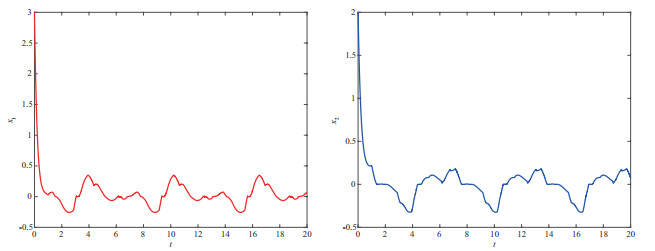
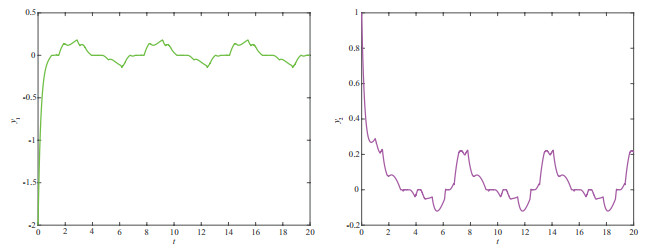
5 仿真结果
本节给出一个实例来验证上述的结果.
例5.1 考虑下述由两个神经元构成的复数神经网络:
其中
其中
图 1
图 2
6 结论
近年来,复数神经网络的动力学性质的研究得到了广泛而深入的研究,但是对具有不连续激活函数的复数神经网络的研究还很缺乏.本文针对一类具有不连续激活函数的复数神经网络的周期性进行了研究,利用Filippov微分包含理论,得到了周期解指数稳定性的充分条件.下一步,我们将对具有更广泛类型的不连续激活函数的复数神经网络的动力学性质进行进一步探讨.
参考文献
Solving the XOR problem and the detection of symmetry using a single complex-valued neuron
DOI:10.1016/S0893-6080(03)00168-0 [本文引用: 1]
Global convergence of neural networks with discontinuous neuron activations
DOI:10.1109/TCSI.2003.818614 [本文引用: 1]
Dynamical behaviors of delayed neural network systems with discontinuous activation functions
DOI:10.1162/neco.2006.18.3.683 [本文引用: 2]
Dynamical behaviors of a class of recurrent neural networks with discontinuous neuron activations
DOI:10.1016/j.apm.2009.03.014 [本文引用: 1]
Stability analysis of Cohen-Grossberg neural networks with discontinuous neuron activations
DOI:10.1016/j.apm.2009.04.016 [本文引用: 1]
Existence and global asymptotic stability of periodic solutions for Hopfield neural networks with discontinuous activations
DOI:10.1016/j.nonrwa.2008.02.022 [本文引用: 7]
Periodicity and global exponential stability of generalized Cohen-Grossberg neural networks with discontinuous activations and mixed delays
DOI:10.1016/j.neunet.2013.12.005
Global exponential stability of uncertain neural networks with discontinuous Lurie-type activation and mixed delays
DOI:10.1016/j.neucom.2015.07.147
Global asymptotical stability analysis for a kind of discrete-time recurrent neural network with discontinuous activation functions
DOI:10.1016/j.neucom.2016.02.017 [本文引用: 2]
Discrete-time recurrent neural networks with complex-valued linear threshold neurons
DOI:10.1109/TCSII.2009.2025625 [本文引用: 1]
Global stability of complex-valued recurrent neural networks with time-delays
DOI:10.1109/TNNLS.2012.2195028
Global stability of complex-valued neural networks with both leakage time delay and discrete time delay on time scales
DOI:10.1016/j.neucom.2013.04.040
Global exponential periodicity and stability of discrete-time complex-valued recurrent neural networks with time-delays
DOI:10.1016/j.neunet.2015.03.001
Global exponential stability for complex-valued recurrent neural networks with asynchronous time delays
Multistability of complex-valued neural networks with time-varying delays
DOI:10.1016/j.amc.2016.08.054 [本文引用: 1]
Dynamical behavior of complex-valued hopfield neural networks with discontinuous activation functions
DOI:10.1007/s11063-016-9563-5 [本文引用: 2]
Note on the derivative with respect to a parameter of the solutions of a system of differential equations
The stability of solutions of linear differential equations
DOI:10.1215/S0012-7094-43-01059-2 [本文引用: 1]