数学物理学报, 2019, 39(5): 1064-1076 doi:

论文

(3+1)维广义Kadomtsev-Petviashvili方程新的精确周期孤立波解

李颖,1, 刘建国2, 阳连武1

New Exact Periodic Solitary Wave Solutions for the (3+1)-Dimensional Generalized Kadomtsev-Petviashvili Equation

Li Ying,1, Liu Jianguo2, Yang Lianwu1

通讯作者: 李颖, E-mail: jxsdsxx@bupt.edu.cn

收稿日期: 2018-08-30  

基金资助: 国家自然科学基金.  61377067
江西省教育厅科技项目.  GJJ170889

Received: 2018-08-30  

Fund supported: the NSFC.  61377067
the Jiangxi Provincial Department of Education.  GJJ170889

摘要

该文研究了广义Kadomtsev-Petviashvili方程，该方程是依赖于横坐标的小振幅慢波非线性长波演化方程.利用Hirota的双线性形式与扩展同宿测试方法，（3+1）维广义Kadomtsev-Petviashvili方程新的精确周期孤立波解被获得，这些获得的结果和已知文献中的结论都不同.在符号计算的帮助下，这些新的周期波精确解的性质和特点通过一些图形进行了展示.

关键词： Hirota双线性形式 ; 周期孤立波解 ; 扩展同宿测试方法 ; 广义Kadomtsev-Petviashvili方程

Abstract

In this paper, we investigate the generalized Kadomtsev-Petviashvili equation for the evolution of nonlinear, long waves of small amplitude with slow dependence on the transverse coordinate. By virtue of the Hirota's bilinear form and the extended homoclinic test approach, new exact periodic solitary wave solutions for the (3+1)-dimensional generalized KadomtsevPetviashvili equation are obtained, which is different from those in previous literatures. With the aid of symbolic computation, the properties and characteristics for these new exact periodic wave solutions are presented with some figures.

Keywords： Hirota's bilinear form ; Periodic solitary wave solutions ; Extended homoclinic test approach ; Generalized Kadomtsev-Petviashvili equation

PDF (2781KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

李颖, 刘建国, 阳连武. (3+1)维广义Kadomtsev-Petviashvili方程新的精确周期孤立波解. 数学物理学报[J], 2019, 39(5): 1064-1076 doi:

Li Ying, Liu Jianguo, Yang Lianwu. New Exact Periodic Solitary Wave Solutions for the (3+1)-Dimensional Generalized Kadomtsev-Petviashvili Equation. Acta Mathematica Scientia[J], 2019, 39(5): 1064-1076 doi:

1 引言

流体力学、等离子体物理、流体力学、光纤、水波、混沌理论、化学物理等领域都出现了许多非线性现象.随着非线性动力学的发展,对这些非线性偏微分方程（NLPDES）的研究对于深入了解这些方程的定性特征越来越重要.为了进一步了解这些非线性现象,寻求非线性偏微分方程的孤立波解成为非线性动力学研究的一个重要课题.在符号计算的帮助下[1-26],许多求解方法被发现,比如反演散射方法[27], Hirota直接方法[28-32],齐次平衡法[33]等等.

本文基于Hirota的双线性形式和扩展同宿测试方法,我们将考虑以下(3+1)维广义Kadomtsev-Petviashvili(KP)方程[34]

$ \begin{equation} u_{ty}+u_{tx}-u_{zz}+3 (u_x\, u_y)_x+u_{xxxy} = 0, \end{equation} $

其中$ u = u(x, y, z, t) $.方程(1.1)是在文献[35]中被获得.如果$ y = x $,方程(1.1)能够变成KP方程.该方程在文献[36]中进行了研究,建立了任意波数的指数型和有理型行波解.该方程也在文献[35]中进行了研究,获得了包括极化周期孤波解,周期孤子解和周期性扭结解的新精确解.该方程在文献[18]中讨论过,提出了Wronskian和Grammian公式.通过使用简化Hirota方法和符号计算[37-52]得出方程(1.1)多孤子解.

本文的结构如下:在第2节中,使用Hirota的双线性形式和扩展的同宿测试方法, (3+1)维广义KP方程新的精确周期孤立波解被获得;在第3节中,给出总结.

2 (3+1)维广义KP方程新的精确周期孤立波解

做因变量变换$ u = 2(\ln\psi)_x $,方程(1.1)有如下双线性形式

$ \begin{equation} (D_t D_x+D_t D_y+D_x^3 D_y-D_z^2) \psi\cdot \psi = 0, \end{equation} $

即

$ \begin{equation} (\psi_{xxxy}+\psi_{tx}+\psi_{ty}-\psi_{zz})\, \psi-3 \psi_{xxy} \psi_x+3 \psi_{xy}\, \psi_{xx}-\psi_{y}\, \psi_{xxx}-\psi_t \psi_x-\psi_t \psi_y+\psi_z^2 = 0. \end{equation} $

根据扩展的同宿测试方法[42],我们假设方程(2.2)有下列形式的解

$ \begin{equation} \psi(x, y, z, t) = k_1\, e^{\Theta _1}+e^{-\Theta _1}+k_2\, \cos \left(\Theta _2\right) + k_3\, \sin \left(\Theta _3\right), \end{equation} $

其中$ \Theta_i = {\cal I}_i\, x+{\cal J}_i\, y+{\cal K}_i\, z+{\cal L}_i\, t, i = 1, 2, 3 $, $ {\cal I} _i $, $ {\cal J} _i $, $ {\cal K} _i $以及$ {\cal L} _i $都是未知常数.将方程(2.3)代入方程(2.2)中,令函数$ e^{\Theta _1} $, $ e^{-\Theta _1} $, $ \sin \left(\Theta _2\right) $, $ \cos \left(\Theta _2\right) $, $ \sin \left(\Theta _3\right) $, $ \cos \left(\Theta _3\right) $不同幂次的系数以及常数项为0,可得

$ \begin{eqnarray} &&k_1 k_2 [{\cal J} _1 {\cal I} _1^3-3 {\cal I} _2 {\cal J} _2 {\cal I} _1^2+\left({\cal L} _1-3 {\cal I} _2^2 {\cal J} _1\right) {\cal I} _1-{\cal K} _1^2+{\cal K} _2^2\\&&+{\cal I} _2^3 {\cal J} _2+{\cal J} _1 {\cal L} _1-\left({\cal I} _2+{\cal J} _2\right) {\cal L} _2] = 0, \end{eqnarray} $

$ \begin{eqnarray} &&k_1 k_2 [{\cal J} _2 {\cal I} _1^3+3 {\cal I} _2 {\cal J} _1 {\cal I} _1^2-3 {\cal I} _2^2 {\cal J} _2 {\cal I} _1-{\cal I} _2^3 {\cal J} _1-2 {\cal K} _1 {\cal K} _2+{\cal I} _2 {\cal L} _1\\&&+{\cal J} _2 {\cal L} _1+\left({\cal I} _1+{\cal J} _1\right) {\cal L} _2] = 0, \end{eqnarray} $

$ \begin{eqnarray} &&k_1 k_3 [{\cal J} _1 {\cal I} _1^3-3 {\cal I} _3 {\cal J} _3 {\cal I} _1^2+\left({\cal L} _1-3 {\cal I} _3^2 {\cal J} _1\right) {\cal I} _1-{\cal K} _1^2+{\cal K} _3^2+{\cal I} _3^3 {\cal J} _3\\&&+{\cal J} _1 {\cal L} _1-\left({\cal I} _3+{\cal J} _3\right) {\cal L} _3] = 0, \end{eqnarray} $

$ \begin{eqnarray} &&k_1 k_3 [{\cal J} _3 {\cal I} _1^3+3 {\cal I} _3 {\cal J} _1 {\cal I} _1^2-3 {\cal I} _3^2 {\cal J} _3 {\cal I} _1-{\cal I} _3^3 {\cal J} _1-2 {\cal K} _1 {\cal K} _3+{\cal I} _3 {\cal L} _1\\&&+{\cal J} _3 {\cal L} _1+\left({\cal I} _1+{\cal J} _1\right) {\cal L} _3] = 0, \end{eqnarray} $

$ \begin{eqnarray} &&k_2 k_3 [-{\cal J} _3 {\cal I} _2^3-3 {\cal I} _3 {\cal J} _2 {\cal I} _2^2-3 {\cal I} _3^2 {\cal J} _3 {\cal I} _2-{\cal I} _3^3 {\cal J} _2-2 {\cal K} _2 {\cal K} _3+{\cal I} _3 {\cal L} _2\\&&+{\cal J} _3 {\cal L} _2+\left({\cal I} _2+{\cal J} _2\right) {\cal L} _3] = 0, \end{eqnarray} $

$ \begin{eqnarray} &&k_2 k_3 [{\cal J} _2 {\cal I} _2^3+3 {\cal I} _3 {\cal J} _3 {\cal I} _2^2+\left(3 {\cal I} _3^2 {\cal J} _2-{\cal L} _2\right) {\cal I} _2+{\cal K} _2^2+{\cal K} _3^2+{\cal I} _3^3 {\cal J} _3\\&&-{\cal J} _2 {\cal L} _2-\left({\cal I} _3+{\cal J} _3\right) {\cal L} _3] = 0, \end{eqnarray} $

$ \begin{eqnarray} &&k_2 k_3 [{\cal J} _3 {\cal I} _2^3+3 {\cal I} _3 {\cal J} _2 {\cal I} _2^2+3 {\cal I} _3^2 {\cal J} _3 {\cal I} _2 -{\cal J} _3 {\cal L} _2+{\cal J} _2 \left({\cal I} _3^3-{\cal L} _3\right)] = 0, \end{eqnarray} $

$ \begin{eqnarray} &&k_3^2 [4 {\cal J} _3 {\cal I} _3^3+{\cal K} _3^2-\left({\cal I} _3+{\cal J} _3\right) {\cal L} _3] = 0, \end{eqnarray} $

$ \begin{eqnarray} &&k_2^2 [4 {\cal J} _2 {\cal I} _2^3+{\cal K} _2^2-\left({\cal I} _2+{\cal J} _2\right) {\cal L} _2] = 0, \end{eqnarray} $

$ \begin{eqnarray} &&k_2 [{\cal J} _1 {\cal I} _1^3-3 {\cal I} _2 {\cal J} _2 {\cal I} _1^2+\left({\cal L} _1-3 {\cal I} _2^2 {\cal J} _1\right) {\cal I} _1-{\cal K} _1^2+{\cal K} _2^2+{\cal I} _2^3 {\cal J} _2\\&&+{\cal J} _1 {\cal L} _1-\left({\cal I} _2+{\cal J} _2\right) {\cal L} _2] = 0, \end{eqnarray} $

$ \begin{eqnarray} &&k_3 [{\cal J} _3 {\cal I} _1^3+3 {\cal I} _3 {\cal J} _1 {\cal I} _1^2-3 {\cal I} _3^2 {\cal J} _3 {\cal I} _1-{\cal I} _3^3 {\cal J} _1-2 {\cal K} _1 {\cal K} _3\\ &&+{\cal I} _3 {\cal L} _1+{\cal J} _3 {\cal L} _1+\left({\cal I} _1+{\cal J} _1\right) {\cal L} _3] = 0, \end{eqnarray} $

$ \begin{eqnarray} &&k_2 [{\cal J} _2 {\cal I} _1^3+3 {\cal I} _2 {\cal J} _1 {\cal I} _1^2-3 {\cal I} _2^2 {\cal J} _2 {\cal I} _1-{\cal I} _2^3 {\cal J} _1-2 {\cal K} _1 {\cal K} _2\\&&+{\cal I} _2 {\cal L} _1+{\cal J} _2 {\cal L} _1+\left({\cal I} _1+{\cal J} _1\right) {\cal L} _2] = 0, \end{eqnarray} $

$ \begin{eqnarray} &&k_3 [{\cal J} _1 {\cal I} _1^3-3 {\cal I} _3 {\cal J} _3 {\cal I} _1^2+\left({\cal L} _1-3 {\cal I} _3^2 {\cal J} _1\right) {\cal I} _1-{\cal K} _1^2+{\cal K} _3^2+{\cal I} _3^3 {\cal J} _3\\&&+{\cal J} _1 {\cal L} _1-\left({\cal I} _3+{\cal J} _3\right) {\cal L} _3] = 0. \end{eqnarray} $

利用符号计算求解以上方程组,可得如下不同形式的解:

情形一  当$ k_3 = 0 $时,方程(1.1)的精确解包括纽结周期孤立波解,周期孤子解和方程的周期扭结解已在文献[34]中讨论过.

情形二

$ \begin{eqnarray} k_1 & = & k_2 = 0, {\cal L}_2 = \frac{4 {\cal J} _2 {\cal I} _2^3+{\cal K} _2^2}{{\cal I} _2+{\cal J} _2}, {\cal L}_3 = \frac{4 {\cal J} _3 {\cal I} _3^3+{\cal K} _3^2}{{\cal I} _3+{\cal J} _3}, \\ {\cal L}_1& = & \frac{-{\cal J} _1 {\cal I} _1^3+3 {\cal I} _3 {\cal J} _3 {\cal I} _1^2+3 {\cal I} _3^2 {\cal J} _1 {\cal I} _1+{\cal K} _1^2+3 {\cal I} _3^3 {\cal J} _3}{{\cal I} _1+{\cal J} _1}, \\ {\cal K}_1 & = & [\left({\cal I} _1+{\cal J} _1\right) \left({\cal I} _3+{\cal J} _3\right) {\cal K} _3+[-\left({\cal I} _3+{\cal J} _3\right)^2 [{\cal J} _3 \left({\cal I} _3+{\cal J} _3\right) {\cal I} _1^4\\&&+2 {\cal I} _3 {\cal J} _1 \left({\cal I} _3+{\cal J} _3\right) {\cal I} _1^3+{\cal I} _3 [4 {\cal J} _3 {\cal I} _3^2+3 \left({\cal J} _1^2+{\cal J} _3^2\right) {\cal I} _3+3 {\cal J} _3 \left({\cal J} _1^2+{\cal J} _3^2\right)] {\cal I} _1^2\\&&+2 {\cal I} _3^3 {\cal J} _1 \left({\cal I} _3+5 {\cal J} _3\right) {\cal I} _1+{\cal I} _3^3 [3 {\cal J} _3^3+6 {\cal I} _3 {\cal J} _3^2\\&&+3 \left({\cal I} _3^2+{\cal J} _1^2\right) {\cal J} _3-{\cal I} _3 {\cal J} _1^2]]]^{1/2} \epsilon _1]/[\left({\cal I} _3+{\cal J} _3\right)^2], \end{eqnarray} $

其中$ {\cal I}_1 $, $ {\cal I}_2 $, $ {\cal I}_3 $, $ {\cal J}_1 $, $ {\cal J}_2 $, $ {\cal J}_3 $, $ {\cal K}_2 $, $ {\cal K}_3 $和$ k_3 $是任意常数, $ \epsilon _1 = \pm1 $.将这些结果代入方程(2.3),可得

$ \begin{eqnarray} \psi & = & e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-\frac{t \left(-{\cal J} _1 {\cal I} _1^3+3 {\cal I} _3 {\cal J} _3 {\cal I} _1^2+3 {\cal I} _3^2 {\cal J} _1 {\cal I} _1+{\cal K} _1^2+3 {\cal I} _3^3 {\cal J} _3\right)}{{\cal I} _1+{\cal J} _1}}\\ &&+ \sin [x {\cal I} _3+y {\cal J} _3+z {\cal K} _3+\frac{t \left(4 {\cal J} _3 {\cal I} _3^3+{\cal K} _3^2\right)}{{\cal I} _3+{\cal J} _3}] k_3. \end{eqnarray} $

因此,我们获得了方程(1.1)第一种新周期孤立波解

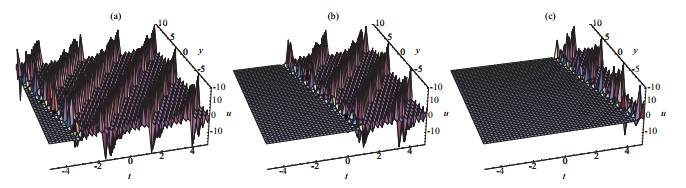
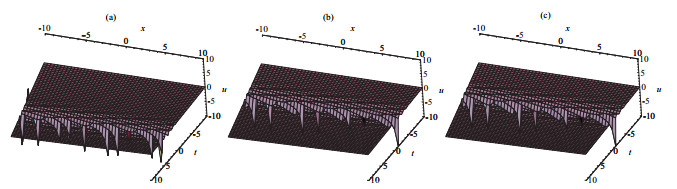
$ \begin{eqnarray} u_1 & = & [2 [-e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-\frac{t \left(-{\cal J} _1 {\cal I} _1^3+3 {\cal I} _3 {\cal J} _3 {\cal I} _1^2+3 {\cal I} _3^2 {\cal J} _1 {\cal I} _1+{\cal K} _1^2+3 {\cal I} _3^3 {\cal J} _3\right)}{{\cal I} _1+{\cal J} _1}} {\cal I} _1+\cos [x {\cal I} _3\\ &&+y {\cal J} _3+z {\cal K} _3+\frac{t \left(4 {\cal J} _3 {\cal I} _3^3+{\cal K} _3^2\right)}{{\cal I} _3+{\cal J} _3}] k_3 {\cal I} _3]]/[\sin [x {\cal I} _3+y {\cal J} _3+\frac{t \left(4 {\cal J} _3 {\cal I} _3^3+{\cal K} _3^2\right)}{{\cal I} _3+{\cal J} _3}\\ &&+z {\cal K} _3] k_3+e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-\frac{t \left(-{\cal J} _1 {\cal I} _1^3+3 {\cal I} _3 {\cal J} _3 {\cal I} _1^2+3 {\cal I} _3^2 {\cal J} _1 {\cal I} _1+{\cal K} _1^2+3 {\cal I} _3^3 {\cal J} _3\right)}{{\cal I} _1+{\cal J} _1}}]. \end{eqnarray} $

方程(2.19)的物理结构被展示在图 1.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   $k_3 = -2$, ${\cal J}_3 = -5$, $x = 2$, ${\cal I}_1 = {\cal I}_2 = {\cal I}_3 = {\cal J}_1 = {\cal J}_2 = {\cal K}_2 = {\cal K}_3 = 1$, $\epsilon_1 = 1$, (a) $z = -5$, (b) $z = 0$, (c) $z = 5$


情形三

$ \begin{eqnarray} k_1 & = & 0, {\cal J}_2 = -\frac{{\cal I} _1 {\cal J} _1}{{\cal I} _2}, {\cal J}_3 = -\frac{{\cal I} _1 {\cal J} _1}{{\cal I} _3}, {\cal L}_2 = \frac{{\cal I} _2 \left({\cal K} _2^2-4 {\cal I} _1 {\cal I} _2^2 {\cal J} _1\right)}{{\cal I} _2^2-{\cal I} _1 {\cal J} _1}, \\ {\cal L}_3& = & \frac{{\cal I} _3 \left({\cal K} _3^2-4 {\cal I} _1 {\cal I} _3^2 {\cal J} _1\right)}{{\cal I} _3^2-{\cal I} _1 {\cal J} _1}, {\cal L}_1 = \frac{{\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1}{{\cal I} _1+{\cal J} _1}, \\ {\cal K}_1 & = & [2 {\cal I} _2 \left({\cal I} _1+{\cal J} _1\right) \left({\cal I} _2^2-{\cal I} _1 {\cal J} _1\right) {\cal K} _2+\epsilon_2 [4 {\cal I} _2^2 \left({\cal I} _1+{\cal J} _1\right)^2 \left({\cal I} _2^2-{\cal I} _1 {\cal J} _1\right)^2 {\cal K} _2^2\\&&-4 \left({\cal I} _2^4-2 {\cal I} _1 {\cal J} _1 {\cal I} _2^2+{\cal I} _1^2 {\cal J} _1^2\right) [{\cal J} _1^2 {\cal I} _1^6-3 {\cal J} _1^3 {\cal I} _1^5-{\cal I} _2^2 {\cal J} _1 {\cal I} _1^5+{\cal I} _2^2 {\cal J} _1^2 {\cal I} _1^4\\ &&-6 {\cal I} _2^2 {\cal J} _1^3 {\cal I} _1^3-2 {\cal I} _2^4 {\cal J} _1 {\cal I} _1^3-{\cal I} _2^4 {\cal J} _1^2 {\cal I} _1^2-3 {\cal I} _2^4 {\cal J} _1^3 {\cal I} _1-{\cal I} _2^6 {\cal J} _1 {\cal I} _1-{\cal I} _2^6 {\cal J} _1^2\\ &&+{\cal I} _2^2 \left({\cal I} _1+{\cal J} _1\right)^2 {\cal K} _2^2]]^{1/2}]/ [2 \left({\cal I} _2^4-2 {\cal I} _1 {\cal J} _1 {\cal I} _2^2+{\cal I} _1^2 {\cal J} _1^2\right)], \\ {\cal K}_2 & = & [{\cal I} _2 {\cal I} _3 \left({\cal I} _2^2-{\cal I} _1 {\cal J} _1\right) \left({\cal I} _3^2-{\cal I} _1 {\cal J} _1\right) {\cal K} _3+\epsilon_3 [-{\cal I} _1 {\cal I} _2^2 \left({\cal I} _2-{\cal I} _3\right)^2 \left({\cal I} _2+{\cal I} _3\right)^2\\ &&\times {\cal J} _1 \left({\cal I} _3^2-{\cal I} _1 {\cal J} _1\right)^2 [{\cal I} _2^2 \left({\cal I} _3^2-{\cal I} _1 {\cal J} _1\right)-{\cal I} _1 {\cal J} _1 \left({\cal I} _3^2+3 {\cal I} _1 {\cal J} _1\right)]]^{1/2}]\\ &&/[{\cal I} _2^2 \left({\cal I} _3^2-{\cal I} _1 {\cal J} _1\right)^2], \end{eqnarray} $

其中$ {\cal I}_1 $, $ {\cal I}_2 $, $ {\cal I}_3 $, $ {\cal K}_3 $, $ k_2 $, $ k_3 $以及$ {\cal J}_1 $是任意常数, $ \epsilon _2 = \pm1 $, $ \epsilon _3 = \pm1 $.将这些结果代入方程(2.3),可得

$ \begin{eqnarray} \psi & = & \cos [x {\cal I} _2+\frac{t \left({\cal K} _2^2-4 {\cal I} _1 {\cal I} _2^2 {\cal J} _1\right) {\cal I} _2}{{\cal I} _2^2-{\cal I} _1 {\cal J} _1}+z {\cal K} _2-\frac{y {\cal I} _1 {\cal J} _1}{{\cal I} _2}] k_2+\sin [x {\cal I} _3+z {\cal K} _3\\&&+\frac{t \left({\cal K} _3^2-4 {\cal I} _1 {\cal I} _3^2 {\cal J} _1\right) {\cal I} _3}{{\cal I} _3^2-{\cal I} _1 {\cal J} _1}-\frac{y {\cal I} _1 {\cal J} _1}{{\cal I} _3}] k_3+e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}}. \end{eqnarray} $

因此,我们获得了方程(1.1)第二种新的周期孤立波解

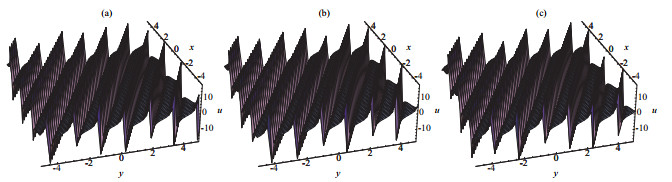
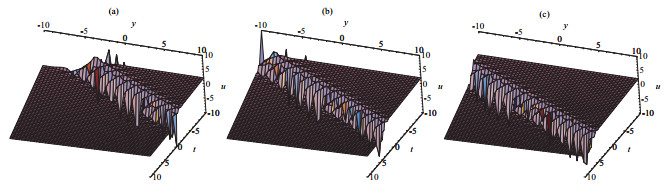
$ \begin{eqnarray} u_2 & = & [2 [-e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}} {\cal I} _1-\sin [x {\cal I} _2+\frac{t \left({\cal K} _2^2-4 {\cal I} _1 {\cal I} _2^2 {\cal J} _1\right) {\cal I} _2}{{\cal I} _2^2-{\cal I} _1 {\cal J} _1}\\&&+z {\cal K} _2-\frac{y {\cal I} _1 {\cal J} _1}{{\cal I} _2}] k_2 {\cal I} _2+\cos [x {\cal I} _3+\frac{t \left({\cal K} _3^2-4 {\cal I} _1 {\cal I} _3^2 {\cal J} _1\right) {\cal I} _3}{{\cal I} _3^2-{\cal I} _1 {\cal J} _1}+z {\cal K} _3-\frac{y {\cal I} _1 {\cal J} _1}{{\cal I} _3}]\\&&\times k_3 {\cal I} _3]]/[\cos [x {\cal I} _2+\frac{t \left({\cal K} _2^2-4 {\cal I} _1 {\cal I} _2^2 {\cal J} _1\right) {\cal I} _2}{{\cal I} _2^2-{\cal I} _1 {\cal J} _1}+z {\cal K} _2-\frac{y {\cal I} _1 {\cal J} _1}{{\cal I} _2}] k_2\\&&+\sin [x {\cal I} _3+\frac{t \left({\cal K} _3^2-4 {\cal I} _1 {\cal I} _3^2 {\cal J} _1\right) {\cal I} _3}{{\cal I} _3^2-{\cal I} _1 {\cal J} _1}+z {\cal K} _3-\frac{y {\cal I} _1 {\cal J} _1}{{\cal I} _3}] k_3 \\ &&+e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}}]. \end{eqnarray} $

方程(2.22)的物理结构被展示在图 2.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   $k_2 = -2$, $\epsilon_2 = -1$, $t = 5$, $\epsilon_3 = -1$, $k_3 = {\cal J}_1 = 2$, ${\cal I}_1 = {\cal I}_2 = {\cal I}_3 = {\cal K}_3 = 1$, $\epsilon_1 = 1$, (a) $z = -5$, (b) $z = 0$, (c) $z = 5$


情形四

$ \begin{eqnarray} k_1 & = & 0, {\cal I} _3 = {\cal I} _2 \epsilon _4, {\cal L}_2 = \frac{4 {\cal J} _2 {\cal I} _2^3+{\cal K} _2^2}{{\cal I} _2+{\cal J} _2}, {\cal L}_3 = \frac{4 {\cal J} _3 \epsilon _4 {\cal I} _2^3+{\cal K} _3^2}{{\cal J} _3+{\cal I} _2 \epsilon _4}, \\ {\cal L}_1 & = & \frac{-{\cal J} _1 {\cal I} _1^3+3 {\cal I} _2 {\cal J} _3 \epsilon _4 {\cal I} _1^2+3 {\cal I} _2^2 {\cal J} _1 {\cal I} _1+{\cal K} _1^2+3 {\cal I} _2^3 {\cal J} _3 \epsilon _4}{{\cal I} _1+{\cal J} _1}, \\ {\cal K}_2& = &[2 [{\cal I} _2^4 [{\cal J} _3^4+{\cal I} _2^2 {\cal J} _3^2+{\cal J} _2^2 {\cal J} _3^2-4 {\cal I} _2 {\cal J} _2 {\cal J} _3^2+2 \left({\cal I} _2-{\cal J} _2\right) \left({\cal J} _3^2-{\cal I} _2 {\cal J} _2\right) \epsilon _4 {\cal J} _3\\ &&+{\cal I} _2^2 {\cal J} _2^2]]^{1/2} \epsilon _5+\left({\cal I} _2+{\cal J} _2\right) {\cal K} _3 \left({\cal J} _3+{\cal I} _2 \epsilon _4\right)]/[{\cal I} _2^2+2 {\cal J} _3 \epsilon _4 {\cal I} _2+{\cal J} _3^2], \end{eqnarray} $

其中$ {\cal I}_1 $, $ {\cal I}_2 $, $ {\cal J}_1 $, $ {\cal J}_2 $, $ {\cal J}_3 $, $ {\cal K}_1 $, $ {\cal K}_3 $, $ k_2 $以及$ k_3 $是任意常数, $ \epsilon _4 = \pm1 $, $ \epsilon _5 = \pm1 $.将这些结果代入方程(2.3),可得

$ \begin{eqnarray} \psi & = & \cos [x {\cal I} _2+y {\cal J} _2+z {\cal K} _2+\frac{t \left(4 {\cal J} _2 {\cal I} _2^3+{\cal K} _2^2\right)}{{\cal I} _2+{\cal J} _2}] k_2+e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-t {\cal L} _1}\\&&+\sin [y {\cal J} _3+z {\cal K} _3+x {\cal I} _2 \epsilon _4+\frac{t \left(4 {\cal I} _2^3 {\cal J} _3 \epsilon _4^3+{\cal K} _3^2\right)}{{\cal J} _3+{\cal I} _2 \epsilon _4}] k_3. \end{eqnarray} $

因此,我们获得了方程(1.1)第三种周期孤立波解

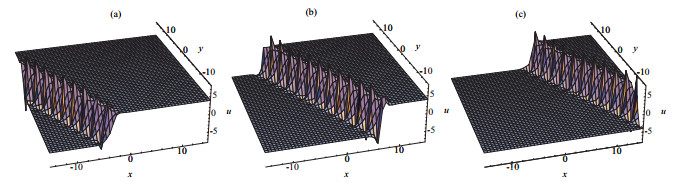
$ \begin{eqnarray} u_3 & = & [2 [-e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-t {\cal L} _1} {\cal I} _1-\sin [x {\cal I} _2+y {\cal J} _2+z {\cal K} _2+\frac{t \left(4 {\cal J} _2 {\cal I} _2^3+{\cal K} _2^2\right)}{{\cal I} _2+{\cal J} _2}]\\ &&\times k_2 {\cal I} _2+\cos [y {\cal J} _3+z {\cal K} _3+x {\cal I} _2 \epsilon _4+\frac{t \left(4 {\cal I} _2^3 {\cal J} _3 \epsilon _4^3+{\cal K} _3^2\right)}{{\cal J} _3+{\cal I} _2 \epsilon _4}]k_3 {\cal I} _2 \epsilon _4]]/[\cos [x {\cal I} _2\\ &&+y {\cal J} _2+z {\cal K} _2+\frac{t \left(4 {\cal J} _2 {\cal I} _2^3+{\cal K} _2^2\right)}{{\cal I} _2+{\cal J} _2}] k_2+e^{-x {\cal I} _1 -y {\cal J} _1-z {\cal K} _1-t {\cal L} _1}\\ &&+\sin [y {\cal J} _3+z {\cal K} _3+x {\cal I} _2 \epsilon _4+\frac{t \left(4 {\cal I} _2^3 {\cal J} _3 \epsilon _4^3+{\cal K} _3^2\right)}{{\cal J} _3+{\cal I} _2 \epsilon _4}] k_3]. \end{eqnarray} $

方程(2.25)的物理结构被展示在图 3.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   $\epsilon_4 = \epsilon_5 = 1$, $k_3 = -2$, ${\cal I}_1 = {\cal I}_2 = {\cal K}_1 = k_2 = {\cal J}_1 = {\cal J}_2 = {\cal J}_3 = {\cal K}_3 = 1$, $z = 2$, (a) $t = -2$, (b) $t = 0$, (c) $t = 2$


情形五

$ \begin{eqnarray} k_2& = &0, {\cal J} _3 = -\frac{{\cal I} _1 {\cal J} _1}{{\cal I} _3}, {\cal L}_3 = \frac{{\cal K} _3^2-4 {\cal I} _1 {\cal I} _3^2 {\cal J} _1}{{\cal I} _3-\frac{{\cal I} _1 {\cal J} _1}{{\cal I} _3}}, {\cal L}_1 = \frac{{\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1}{{\cal I} _1+{\cal J} _1}, \\ {\cal K}_3& = &[{\cal I} _3 \left({\cal I} _1+{\cal J} _1\right) \left({\cal I} _3^2-{\cal I} _1 {\cal J} _1\right) {\cal K} _1+[{\cal I} _3^2 \left({\cal I} _1^2+{\cal I} _3^2\right)^2 {\cal J} _1 \left({\cal I} _1+{\cal J} _1\right)^2 [-{\cal J} _1 {\cal I} _1^2\\ &&+\left({\cal I} _3^2+3 {\cal J} _1^2\right) {\cal I} _1+{\cal I} _3^2 {\cal J} _1]]^{1/2} \epsilon _6]/[{\cal I} _3^2 \left({\cal I} _1+{\cal J} _1\right)^2], \end{eqnarray} $

其中$ {\cal I}_1 $, $ {\cal I}_2 $, $ {\cal I}_3 $, $ {\cal J}_1 $, $ {\cal J}_2 $, $ {\cal L}_2 $, $ {\cal K}_1 $, $ {\cal K}_2 $, $ k_1 $和$ k_3 $是任意常数, $ \epsilon _6 = \pm1 $.将这些结果代入方程(2.3),可得

$ \begin{eqnarray} \psi & = & e^{x {\cal I} _1+y {\cal J} _1+z {\cal K} _1+\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}} k_1+e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}}\\&&+\sin [x {\cal I} _3+z {\cal K} _3+\frac{t \left({\cal K} _3^2-4 {\cal I} _1 {\cal I} _3^2 {\cal J} _1\right)}{{\cal I} _3 -\frac{{\cal I} _1 {\cal J} _1}{{\cal I} _3}}-\frac{y {\cal I} _1 {\cal J} _1}{{\cal I} _3}] k_3. \end{eqnarray} $

因此,我们获得了方程(1.1)第四种新的周期孤立波解

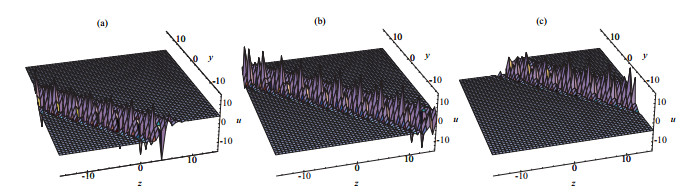
$ \begin{eqnarray} u_4 & = & [2 [-e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}} {\cal I} _1+e^{x {\cal I} _1+y {\cal J} _1+z {\cal K} _1+\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}} k_1 {\cal I} _1\\&&+\cos [x {\cal I} _3+z {\cal K} _3+\frac{t \left({\cal K} _3^2-4 {\cal I} _1 {\cal I} _3^2 {\cal J} _1\right)}{{\cal I} _3-\frac{{\cal I} _1 {\cal J} _1}{{\cal I} _3}}-\frac{y {\cal I} _1 {\cal J} _1}{{\cal I} _3}] k_3 {\cal I} _3]]\\ &&/[e^{x {\cal I} _1+y {\cal J} _1+z {\cal K} _1+\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}} k_1+e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}}\\ &&+\sin [x {\cal I} _3+z {\cal K} _3+\frac{t \left({\cal K} _3^2-4 {\cal I} _1 {\cal I} _3^2 {\cal J} _1\right)}{{\cal I} _3-\frac{{\cal I} _1 {\cal J} _1}{{\cal I} _3}}-\frac{y {\cal I} _1 {\cal J} _1}{{\cal I} _3}] k_3]. \end{eqnarray} $

方程(2.28)的物理结构被展示在图 4.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   ${\cal I}_1 = {\cal K}_2 = z = 2$, ${\cal I}_3 = -1$, ${\cal I}_2 = 3$, $k_1 = {\cal J}_1 = {\cal K}_1 = 1$, $k_3 = -2$, ${\cal J}_2 = 4$, ${\cal L}_2 = 5$, $\epsilon _6 = 1$, (a) $t = -2$, (b) $t = 0$, (c) $t = 2$


情形六

$ \begin{eqnarray} k_2 & = & 0, {\cal I} _3 = {\cal I} _1 \epsilon _7 {\rm i}, {\cal L}_3 = \frac{{\cal K} _3^2-4 {\rm i} {\cal I} _1^3 {\cal J} _3 \epsilon _7}{{\cal J} _3+{\rm i} {\cal I} _1 \epsilon _7}, \\ {\cal L}_1 & = & \frac{{\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1}{{\cal I} _1+{\cal J} _1}, {\cal K}_3 = \frac{2 {\rm i} {\cal J} _3 \epsilon _8 {\cal I} _1^2+2 {\cal J} _1 \epsilon _7 \epsilon _8 {\cal I} _1^2+{\rm i} {\cal K} _1 \epsilon _7 {\cal I} _1+{\cal J} _3 {\cal K} _1}{{\cal I} _1+{\cal J} _1}, \end{eqnarray} $

其中$ {\cal I}_1 $, $ {\cal I}_2 $, $ {\cal J}_1 $, $ {\cal J}_2 $, $ {\cal J}_3 $, $ {\cal L}_2 $, $ {\cal K}_1 $, $ {\cal K}_2 $, $ k_1 $以及$ k_3 $是任意常数, $ \epsilon _7 = \pm1 $, $ \epsilon _8 = \pm1 $.将这些结果代入方程(2.3),可得

$ \begin{eqnarray} \psi & = & e^{x {\cal I} _1+y {\cal J} _1+z {\cal K} _1+\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}} k_1+e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}}\\ &&+\sin [y {\cal J} _3+z {\cal K} _3+{\rm i} x {\cal I} _1 \epsilon _7+\frac{t \left({\cal K} _3^2 -4 {\rm i} {\cal I} _1^3 {\cal J} _3 \epsilon _7\right)}{{\cal J} _3+{\rm i} {\cal I} _1 \epsilon _7}] k_3. \end{eqnarray} $

因此,我们获得了方程(1.1)第五种新的周期孤立波解

$ \begin{eqnarray} u_5 & = & [2 [-e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}} {\cal I} _1+e^{x {\cal I} _1+y {\cal J} _1+z {\cal K} _1+\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}} k_1 {\cal I} _1\\ &&+{\rm i} \cos [y {\cal J} _3+z {\cal K} _3+{\rm i} x {\cal I} _1 \epsilon _7+\frac{t \left({\cal K} _3^2-4 {\rm i} {\cal I} _1^3 {\cal J} _3 \epsilon _7\right)}{{\cal J} _3+{\rm i} {\cal I} _1 \epsilon _7}] k_3 \epsilon _7 {\cal I} _1]]\\ &&/[e^{x {\cal I} _1+y {\cal J} _1+z {\cal K} _1+\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}} k_1+e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-\frac{t \left({\cal K} _1^2-4 {\cal I} _1^3 {\cal J} _1\right)}{{\cal I} _1+{\cal J} _1}}\\ &&+\sin [y {\cal J} _3+z {\cal K} _3+{\rm i} x {\cal I} _1 \epsilon _7+\frac{t \left({\cal K} _3^2-4 {\rm i} {\cal I} _1^3 {\cal J} _3 \epsilon _7\right)}{{\cal J} _3+{\rm i} {\cal I} _1 \epsilon _7}] k_3]. \end{eqnarray} $

情形七

$ \begin{eqnarray} {\cal I}_1 & = & \frac{{\cal I} _2 {\cal J} _3}{{\cal J} _1}, \quad {\cal I}_3 = -{\cal I} _2, \quad {\cal J} _2 = - {\cal J} _3, \\ {\cal L}_1 & = & \frac{{\cal J} _1^2 {\cal K} _1^2-4 {\cal I} _2^3 {\cal J} _3^3}{{\cal J} _1^3+{\cal I} _2 {\cal J} _3 {\cal J} _1}, \quad {\cal L}_2 = \frac{{\cal K} _2^2-4 {\cal I} _2^3 {\cal J} _3}{{\cal I} _2-{\cal J} _3}, \quad {\cal L}_3 = \frac{{\cal K} _3^2-4 {\cal I} _2^3 {\cal J} _3}{{\cal J} _3-{\cal I} _2}, \\ {\cal K}_2& = &[{\cal J} _1 [\left({\cal I} _2-{\cal J} _3\right) {\cal J} _3 {\cal K} _1 {\cal I} _2^3+{\cal J} _1^2 \left({\cal I} _2-{\cal J} _3\right) {\cal K} _1 {\cal I} _2^2\\ &&-{\cal J} _1 \sqrt{\frac{{\cal I} _2^7 \left({\cal J} _1^2+{\cal I} _2 {\cal J} _3\right)^2 \left({\cal J} _1^2+{\cal J} _3^2\right)^2 \left({\cal J} _3 {\cal I} _2^2+\left({\cal J} _1^2-{\cal J} _3^2\right) {\cal I} _2+3 {\cal J} _1^2 {\cal J} _3\right)}{{\cal J} _1^6}} \epsilon _{10}]]\\&&/[{\cal I} _2^2 \left({\cal J} _1^2+{\cal I} _2 {\cal J} _3\right)^2], {\cal K}_3 = [{\cal J} _1 [{\cal I} _2 \left({\cal J} _3-{\cal I} _2\right) {\cal K} _1 {\cal J} _3^5-{\cal J} _1^2 \left({\cal I} _2-{\cal J} _3\right) {\cal K} _1 {\cal J} _3^4\\ &&+{\cal J} _1 \sqrt{\frac{{\cal I} _2^3 {\cal J} _3^8 \left({\cal J} _1^2+{\cal I} _2 {\cal J} _3\right)^2 \left({\cal J} _1^2+{\cal J} _3^2\right)^2 \left({\cal J} _3 {\cal I} _2^2+\left({\cal J} _1^2- {\cal J} _3^2\right) {\cal I} _2+3 {\cal J} _1^2 {\cal J} _3\right)}{{\cal J} _1^6}} \epsilon _9]]\\ &&/[{\cal J} _3^4 \left({\cal J} _1^2+{\cal I} _2 {\cal J} _3\right)^2], \end{eqnarray} $

其中$ {\cal I}_2 $, $ {\cal J}_1 $, $ {\cal J}_3 $, $ {\cal K}_1 $, $ k_1 $, $ k_2 $以及$ k_3 $是任意常数, $ \epsilon _9 = \pm1 $, $ \epsilon _{10} = \pm1 $.将这些结果代入方程(2.3),可得

$ \begin{eqnarray} \psi & = & e^{y {\cal J} _1+z {\cal K} _1+\frac{t \left({\cal J} _1^2 {\cal K} _1^2-4 {\cal I} _2^3 {\cal J} _3^3\right)}{{\cal J} _1^3+{\cal I} _2 {\cal J} _3 {\cal J} _1}+\frac{x {\cal I} _2 {\cal J} _3}{{\cal J} _1}} k_1+\cos [x {\cal I} _2-y {\cal J} _3+z {\cal K} _2\\ &&+\frac{t \left({\cal K} _2^2-4 {\cal I} _2^3 {\cal J} _3\right)}{{\cal I} _2-{\cal J} _3}] k_2+e^{-y {\cal J} _1-z {\cal K} _1-\frac{t \left({\cal J} _1^2 {\cal K} _1^2-4 {\cal I} _2^3 {\cal J} _3^3\right)}{{\cal J} _1^3+{\cal I} _2 {\cal J} _3 {\cal J} _1} -\frac{x {\cal I} _2 {\cal J} _3}{{\cal J} _1}}\\ &&-\sin [x {\cal I} _2-y {\cal J} _3-z {\cal K} _3-\frac{t \left({\cal K} _3^2 -4 {\cal I} _2^3 {\cal J} _3\right)}{{\cal J} _3-{\cal I} _2}] k_3. \end{eqnarray} $

因此,我们获得了方程(1.1)第六种新的周期孤立波解

$ \begin{eqnarray} u_6 & = & [2 [-\sin [x {\cal I} _2-y {\cal J} _3+z {\cal K} _2+\frac{t \left({\cal K} _2^2-4 {\cal I} _2^3 {\cal J} _3\right)}{{\cal I} _2-{\cal J} _3}] k_2 {\cal I} _2-\cos [x {\cal I} _2-y {\cal J} _3-z {\cal K} _3\\ &&-\frac{t \left({\cal K} _3^2-4 {\cal I} _2^3 {\cal J} _3\right)}{{\cal J} _3-{\cal I} _2}] k_3 {\cal I} _2-\frac{e^{-y {\cal J} _1-z {\cal K} _1-\frac{t \left({\cal J} _1^2 {\cal K} _1^2-4 {\cal I} _2^3 {\cal J} _3^3\right)}{{\cal J} _1^3+{\cal I} _2 {\cal J} _3 {\cal J} _1}-\frac{x {\cal I} _2 {\cal J} _3}{{\cal J} _1}} {\cal J} _3 {\cal I} _2}{{\cal J} _1}\\ &&+\frac{e^{y {\cal J} _1+z {\cal K} _1+\frac{t \left({\cal J} _1^2 {\cal K} _1^2-4 {\cal I} _2^3 {\cal J} _3^3\right)}{{\cal J} _1^3+{\cal I} _2 {\cal J} _3 {\cal J} _1}+\frac{x {\cal I} _2 {\cal J} _3}{{\cal J} _1}} k_1 {\cal J} _3 {\cal I} _2}{{\cal J} _1}]]/[e^{y {\cal J} _1+z {\cal K} _1+\frac{t \left({\cal J} _1^2 {\cal K} _1^2-4 {\cal I} _2^3 {\cal J} _3^3\right)}{{\cal J} _1^3+{\cal I} _2 {\cal J} _3 {\cal J} _1}+\frac{x {\cal I} _2 {\cal J} _3}{{\cal J} _1}} k_1\\ &&+e^{-y {\cal J} _1-z {\cal K} _1-\frac{t \left({\cal J} _1^2 {\cal K} _1^2-4 {\cal I} _2^3 {\cal J} _3^3\right)}{{\cal J} _1^3+{\cal I} _2 {\cal J} _3 {\cal J} _1}-\frac{x {\cal I} _2 {\cal J} _3}{{\cal J} _1}}+\cos [x {\cal I} _2+\frac{t \left({\cal K} _2^2-4 {\cal I} _2^3 {\cal J} _3\right)}{{\cal I} _2-{\cal J} _3}-y {\cal J} _3\\ &&+z {\cal K} _2] k_2-\sin [x {\cal I} _2-y {\cal J} _3-z {\cal K} _3-\frac{t \left({\cal K} _3^2-4 {\cal I} _2^3 {\cal J} _3\right)}{{\cal J} _3-{\cal I} _2}] k_3]. \end{eqnarray} $

方程(2.34)的物理结构被展示在图 5.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   $k_3 = -2$, $\epsilon _9 = \epsilon _{10} = 1$, $x = 0.2$, ${\cal I}_2 = k_1 = k_2 = {\cal J}_1 = {\cal K}_1 = 1$, ${\cal J}_3 = 2$, (a) $t = -1$, (b) $t = 0$, (c) $t = 1$


情形八

$ \begin{eqnarray} {\cal I}_1 & = & {\rm i} {\cal I}_2 \epsilon_{11}, {\cal L}_3 = \frac{4 {\cal J} _3 {\cal I} _3^3+{\cal K} _3^2}{{\cal I} _3+{\cal J} _3}, {\cal L}_2 = \frac{4 {\cal J} _2 {\cal I} _2^3+{\cal K} _2^2}{{\cal I} _2+{\cal J} _2}, {\cal I}_3 = \frac{{\cal I} _2 {\cal J} _2}{{\cal J} _3}, \\ {\cal L}_1& = &\frac{4 {\rm i} {\cal J} _1 \epsilon _{11} {\cal I} _2^3+{\cal K} _1^2}{{\cal J} _1+{\rm i} {\cal I} _2 \epsilon _{11}}, {\cal J}_2 = -{\rm i} {\cal J} _1 \epsilon _{11}, {\cal K}_2 = -\frac{{\rm i} \left({\rm i} {\cal I} _2 {\cal K} _1+{\cal J} _1 \epsilon _{11} {\cal K} _1\right)}{{\cal J} _1+{\rm i} {\cal I} _2 \epsilon _{11}}, \\ {\cal K}_3& = &[{\cal J} _3^3 {\cal K} _1 [{\cal J} _1 [-{\cal I} _2^4+3 \left({\cal J} _1^2-{\cal J} _3^2\right) {\cal I} _2^2+{\cal J} _1^2 {\cal J} _3^2] \epsilon _{11}-{\rm i} {\cal I} _2 [{\cal J} _1^4-3 {\cal J} _3^2 {\cal J} _1^2\\&&+{\cal I} _2^2 \left({\cal J} _3^2-3 {\cal J} _1^2\right)]]-{\rm i} [{\cal I} _2^3 {\cal J} _3^4 \left({\cal J} _1^2+{\cal J} _3^2\right)^2 [{\cal I} _2 [-{\cal J} _1^8+21 {\cal I} _2^2 {\cal J} _1^6-35 {\cal I} _2^4 {\cal J} _1^4\\&&+7 {\cal I} _2^6 {\cal J} _1^2-\left({\cal I} _2^6+3 {\cal J} _1^2 {\cal I} _2^4-45 {\cal J} _1^4 {\cal I} _2^2+17 {\cal J} _1^6\right) {\cal J} _3^2]+{\rm i} {\cal J} _1 [{\cal I} _2^8-21 {\cal J} _1^2 {\cal I} _2^6\\&&+35 {\cal J} _1^4 {\cal I} _2^4-7 {\cal J} _1^6 {\cal I} _2^2+\left(3 {\cal I} _2^6+25 {\cal J} _1^2 {\cal I} _2^4-39 {\cal J} _1^4 {\cal I} _2^2+3 {\cal J} _1^6\right) {\cal J} _3^2] \epsilon _{11}]]^{1/2} \epsilon _{12}]\\&&/[{\cal J} _3^4 \left(\left({\cal I} _2^4-6 {\cal J} _1^2 {\cal I} _2^2+{\cal J} _1^4\right) \epsilon _{11}-4 {\rm i} {\cal I} _2 {\cal J} _1 \left({\cal I} _2^2-{\cal J} _1^2\right)\right)], \end{eqnarray} $

其中$ {\cal I}_2 $, $ {\cal J}_1 $, $ {\cal J}_3 $, $ {\cal K}_1 $, $ k_1 $, $ k_2 $以及$ k_3 $是任意常数, $ \epsilon _{11} = \pm1 $, $ \epsilon _{12} = \pm1 $.将这些结果代入方程(2.3),可得

$ \begin{eqnarray} \psi & = & e^{y {\cal J} _1+z {\cal K} _1+t {\cal L} _1+{\rm i} x {\cal I} _2 \epsilon _{11}} k_1+\sin [y {\cal J} _3+z {\cal K} _3+t {\cal L} _3-\frac{{\rm i} x {\cal I} _2 {\cal J} _1 \epsilon _{11}}{{\cal J} _3}] k_3\\ & &+e^{-y {\cal J} _1-z {\cal K} _1-t {\cal L} _1-{\rm i} x {\cal I} _2 \epsilon _{11}}+\cos [x {\cal I} _2+z {\cal K} _2+t {\cal L} _2-{\rm i} y {\cal J} _1 \epsilon _{11}] k_2. \end{eqnarray} $

因此,我们获得了方程(1.1)第七种新的周期孤立波解

$ \begin{eqnarray} u_7 & = & [2 [-\sin [x {\cal I} _2+z {\cal K} _2+t {\cal L} _2-{\rm i} y {\cal J} _1 \epsilon _{11}] k_2 {\cal I} _2-{\rm i} e^{-y {\cal J} _1-z {\cal K} _1-t {\cal L} _1-{\rm i} x {\cal I} _2 \epsilon _{11}} \epsilon _{11} {\cal I} _2\\&&-\frac{{\rm i} \cos [y {\cal J} _3+z {\cal K} _3+t {\cal L} _3-\frac{{\rm i} x {\cal I} _2 {\cal J} _1 \epsilon _{11}}{{\cal J} _3}] k_3 {\cal J} _1 \epsilon _{11} {\cal I} _2}{{\cal J} _3}+{\rm i} e^{y {\cal J} _1+z {\cal K} _1+t {\cal L} _1+{\rm i} x {\cal I} _2 \epsilon _{11}} k_1\\ &&\times \epsilon _{11} {\cal I} _2]]/[e^{y {\cal J} _1+z {\cal K} _1+t {\cal L} _1+{\rm i} x {\cal I} _2 \epsilon _{11}} k_1+e^{-y {\cal J} _1-z {\cal K} _1-t {\cal L} _1-{\rm i} x {\cal I} _2 \epsilon _{11}}+\cos [x {\cal I} _2+z {\cal K} _2\\&&+t {\cal L} _2-{\rm i} y {\cal J} _1 \epsilon _{11}] k_2+\sin [y {\cal J} _3+z {\cal K} _3+t {\cal L} _3-\frac{{\rm i} x {\cal I} _2 {\cal J} _1 \epsilon _{11}}{{\cal J} _3}] k_3]. \end{eqnarray} $

情形九

$ \begin{eqnarray} {\cal I}_1 & = & {\cal J}_2 = {\cal I}_3 = 0, {\cal L}_1 = \frac{{\cal K} _1^2}{{\cal J} _1}, {\cal L}_2 = \frac{{\cal K} _2^2}{{\cal I} _2}, {\cal L}_3 = \frac{{\cal K} _3^2}{{\cal J} _3}, \\ {\cal K}_3& = &\frac{{\cal J} _3 {\cal K} _1}{{\cal J} _1}, {\cal K}_2 = \frac{{\cal J} _1 \epsilon _{13} {\cal I} _2^2+{\cal K} _1 {\cal I} _2}{{\cal J} _1}, \end{eqnarray} $

其中$ {\cal I}_2 $, $ {\cal J}_1 $, $ {\cal J}_3 $, $ {\cal K}_1 $, $ k_1 $, $ k_2 $以及$ k_3 $是任意常数, $ \epsilon _{13} = \pm1 $.将这些参数的值代入方程(2.3),可得

$ \begin{eqnarray} \psi & = & \cos [\frac{t \left({\cal J} _1 \epsilon _{13} {\cal I} _2^2+{\cal K} _1 {\cal I} _2\right)^2}{{\cal I} _2 {\cal J} _1^2}+\frac{z \left({\cal J} _1 \epsilon _{13} {\cal I} _2^2+{\cal K} _1 {\cal I} _2\right)}{{\cal J} _1}+x {\cal I} _2] k_2+e^{\frac{t {\cal K} _1^2}{{\cal J} _1}+z {\cal K} _1+y {\cal J} _1} k_1\\&&+e^{-\frac{t {\cal K} _1^2}{{\cal J} _1}-z {\cal K} _1-y {\cal J} _1}+\sin [\frac{t {\cal J} _3 {\cal K} _1^2}{{\cal J} _1^2}+\frac{z {\cal J} _3 {\cal K} _1}{{\cal J} _1}+y {\cal J} _3] k_3. \end{eqnarray} $

因此,我们获得了方程(1.1)第八种新的周期孤立波解

$ \begin{eqnarray} u_8 & = & -[2 \sin [\frac{t \left({\cal J} _1 \epsilon _{13} {\cal I} _2^2+{\cal K} _1 {\cal I} _2\right)^2}{{\cal I} _2 {\cal J} _1^2}+\frac{z \left({\cal J} _1 \epsilon _{13} {\cal I} _2^2+{\cal K} _1 {\cal I} _2\right)}{{\cal J} _1}+x {\cal I} _2] k_2 {\cal I} _2]\\&&/[e^{\frac{t {\cal K} _1^2}{{\cal J} _1}+z {\cal K} _1+y {\cal J} _1} k_1+e^{-\frac{t {\cal K} _1^2}{{\cal J} _1}-z {\cal K} _1-y {\cal J} _1}+\sin [\frac{t {\cal J} _3 {\cal K} _1^2}{{\cal J} _1^2}+\frac{z {\cal J} _3 {\cal K} _1}{{\cal J} _1}+y {\cal J} _3] k_3\\&&+\cos [\frac{t \left({\cal J} _1 \epsilon _{13} {\cal I} _2^2+{\cal K} _1 {\cal I} _2\right)^2}{{\cal I} _2 {\cal J} _1^2}+\frac{z \left({\cal J} _1 \epsilon _{13} {\cal I} _2^2+{\cal K} _1 {\cal I} _2\right)}{{\cal J} _1}+x {\cal I} _2] k_2]. \end{eqnarray} $

方程(2.40)的物理结构被展示在图 6.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   $k_3 = -2$, $\epsilon _{13} = 1$, $z = 2$, ${\cal I}_2 = k_1 = k_2 = {\cal J}_1 = {\cal K}_1 = 1$, ${\cal J}_3 = 2$, (a) $y = -5$, (b) $y = 0$, (c) $y = 5$


情形十

$ \begin{eqnarray} {\cal I}_2 & = & -\frac{{\cal I} _1 {\cal J} _1 \epsilon _{14}}{{\cal J} _3}, {\cal L}_3 = \frac{4 {\cal J} _3 {\cal I} _3^3+{\cal K} _3^2}{{\cal I} _3+{\cal J} _3}, {\cal L}_2 = \frac{4 {\cal J} _2 {\cal I} _2^3+{\cal K} _2^2}{{\cal I} _2+{\cal J} _2}, {\cal I}_3 = -\frac{{\cal I} _1 {\cal J} _1 \epsilon _{14}}{{\cal J} _3}, \\ {\cal J}_2& = &{\cal J} _3 \epsilon _{14}, {\cal L}_1 = \frac{-{\cal J} _1 {\cal I} _1^3+3 {\cal I} _2 {\cal J} _2 {\cal I} _1^2+3 {\cal I} _2^2 {\cal J} _1 {\cal I} _1+{\cal K} _1^2+3 {\cal I} _2^3 {\cal J} _2}{{\cal I} _1+{\cal J} _1}, {\cal K}_2 = {\cal K} _3 \epsilon _{14}, \\ {\cal K}_3& = &[\sqrt{{\cal I} _1^3 \left({\cal I} _1+{\cal J} _1\right)^2 {\cal J} _3^4 \left({\cal J} _1^2+{\cal J} _3^2\right)^2 \left({\cal I} _1 {\cal J} _1 \left({\cal I} _1+{\cal J} _1\right)-\left({\cal I} _1-3 {\cal J} _1\right) {\cal J} _3^2\right)} \epsilon _{15}\\&&+\left({\cal I} _1+{\cal J} _1\right) \left({\cal J} _3^2-{\cal I} _1 {\cal J} _1\right) {\cal K} _1 {\cal J} _3^3]/[\left({\cal I} _1+{\cal J} _1\right)^2 {\cal J} _3^4], \end{eqnarray} $

其中$ {\cal I}_1 $, $ {\cal J}_1 $, $ {\cal J}_3 $, $ {\cal K}_1 $, $ k_1 $, $ k_2 $和$ k_3 $是任意常数, $ \epsilon _{14} = \pm1 $, $ \epsilon _{15} = \pm1 $.将这些结果代入方程(2.3),可得

$ \begin{eqnarray} \psi & = & e^{x {\cal I} _1+y {\cal J} _1+z {\cal K} _1+t {\cal L} _1} k_1-\sin [\frac{x {\cal I} _1 {\cal J} _1}{{\cal J} _3}-y {\cal J} _3-z {\cal K} _3-t {\cal L} _3] k_3\\&&+e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-t {\cal L} _1}+\cos [t {\cal L} _2+y {\cal J} _3 \epsilon _{14}+z {\cal K} _3 \epsilon _{14}-\frac{x {\cal I} _1 {\cal J} _1 \epsilon _{14}}{{\cal J} _3}] k_2. \end{eqnarray} $

因此,我们获得了方程(1.1)第九种新的周期孤立波解

$ \begin{eqnarray} u_{9} & = & [2 [-e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-t {\cal L} _1} {\cal I} _1+e^{x {\cal I} _1+y {\cal J} _1+z {\cal K} _1+t {\cal L} _1} k_1 {\cal I} _1\\&&+\frac{\sin [t {\cal L} _2+y {\cal J} _3 \epsilon _{14}+z {\cal K} _3 \epsilon _{14}-\frac{x {\cal I} _1 {\cal J} _1 \epsilon _{14}}{{\cal J} _3}] k_2 {\cal J} _1 \epsilon _{14} {\cal I} _1}{{\cal J} _3}\\&&-\frac{\cos [\frac{x {\cal I} _1 {\cal J} _1}{{\cal J} _3}-y {\cal J} _3-z {\cal K} _3-t {\cal L} _3] k_3 {\cal J} _1 {\cal I} _1}{{\cal J} _3}]]/[e^{x {\cal I} _1+y {\cal J} _1+z {\cal K} _1+t {\cal L} _1} k_1\\&&+e^{-x {\cal I} _1-y {\cal J} _1-z {\cal K} _1-t {\cal L} _1}+\cos [t {\cal L} _2+y {\cal J} _3 \epsilon _{14}+z {\cal K} _3 \epsilon _{14}-\frac{x {\cal I} _1 {\cal J} _1 \epsilon _{14}}{{\cal J} _3}] k_2\\&&-\sin [\frac{x {\cal I} _1 {\cal J} _1}{{\cal J} _3}-y {\cal J} _3-z {\cal K} _3-t {\cal L} _3] k_3]. \end{eqnarray} $

方程(2.43)的物理结构被展示在图 7.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   $k_3 = -2$, $\epsilon _{14} = \epsilon _{15} = 1$, $x = -5$, ${\cal I}_1 = k_1 = k_2 = {\cal J}_1 = {\cal K}_1 = 1$, ${\cal J}_3 = 2$, (a) $z = -5$, (b) $z = 0$, (c) $z = 5$


情形十一

$ \begin{eqnarray} {\cal I}_2 & = & {\cal I}_3 = {\cal J} _1 = 0, {\cal L}_1 = \frac{{\cal K} _1^2}{{\cal I} _1}, {\cal L}_2 = \frac{{\cal K} _2^2}{{\cal J} _2}, {\cal L}_3 = \frac{{\cal K} _3^2}{{\cal J} _3}, \\ {\cal K}_3& = &\frac{{\cal J} _3 {\cal K} _2}{{\cal J} _2}, {\cal K}_1 = {\cal I} _1 \left(\frac{{\cal K} _2}{{\cal J} _2}+{\rm i} {\cal I} _1 \epsilon _{16}\right), \end{eqnarray} $

其中$ {\cal I}_1 $, $ {\cal J}_2 $, $ {\cal J}_3 $, $ {\cal K}_2 $, $ k_1 $, $ k_2 $以及$ k_3 $是任意常数, $ \epsilon _{16} = \pm1 $.将这些结果代入方程(2.3),可得

$ \begin{eqnarray} \psi & = & e^{\frac{t {\cal K} _1^2}{{\cal I} _1}+z {\cal K} _1+x {\cal I} _1} k_1+e^{-\frac{t {\cal K} _1^2}{{\cal I} _1}-z {\cal K} _1-x {\cal I} _1}+\cos [\frac{t {\cal K} _2^2}{{\cal J} _2}+z {\cal K} _2+y {\cal J} _2] k_2\\&&+\sin [\frac{t {\cal J} _3 {\cal K} _2^2}{{\cal J} _2^2}+\frac{z {\cal J} _3 {\cal K} _2}{{\cal J} _2}+y {\cal J} _3] k_3. \end{eqnarray} $

因此,我们获得了方程(1.1)第十种新的周期孤立波解

$ \begin{eqnarray} u_{10} & = & [2 (e^{\frac{t {\cal K} _1^2}{{\cal I} _1}+z {\cal K} _1+x {\cal I} _1} k_1 {\cal I} _1-e^{-\frac{t {\cal K} _1^2}{{\cal I} _1}-z {\cal K} _1-x {\cal I} _1} {\cal I} _1)]/[e^{\frac{t {\cal K} _1^2}{{\cal I} _1}+z {\cal K} _1+x {\cal I} _1} k_1+e^{-\frac{t {\cal K} _1^2}{{\cal I} _1}-z {\cal K} _1-x {\cal I} _1}\\&&+ \cos [\frac{t {\cal K} _2^2}{{\cal J} _2}+z {\cal K} _2+y {\cal J} _2] k_2 +\sin [\frac{t {\cal J} _3 {\cal K} _2^2}{{\cal J} _2^2}+\frac{z {\cal J} _3 {\cal K} _2}{{\cal J} _2}+y {\cal J} _3] k_3]. \end{eqnarray} $

3 总结

本文通过使用Hirota的双线性形式和扩展的同宿测试方法,我们得到了(3+1)维广义KP方程新的精确周期孤立波解.此外,这些新的精确周期波解的物理性质和特性如图 1-图 7所示.

参考文献

Zhou Y , Ma W X .

Complexiton solutions to soliton equations by the Hirota method

J Math Phys, 2017, 58 (10): 101511

DOI:10.1063/1.4996358      [本文引用: 1]

Ma W X , Zhou Y .

Reduced D-Kaup-Newell soliton hierarchies from sl(2, R) and so(3, R)

Int J Geom Methods M, 2016, 13: 1650105

DOI:10.1142/S021988781650105X     

Yang J Y , Ma W X , Qin Z Y .

Lump and lump-soliton solutions to the (2+1)-dimensional Ito equation

Anal Math Phys, 2018, 8: 427- 436

DOI:10.1007/s13324-017-0181-9     

Ma W X , Qin Z Y , Lü X .

Lump solutions to dimensionally reduced p-gKP and p-gBKP equations

Nonlinear Dyn, 2016, 84: 923- 931

DOI:10.1007/s11071-015-2539-6     

邵光明, 柴晓娟.

Navier-Stokes-Fourier方程的可压逼近

数学物理学报, 2017, 37A (6): 1070- 1084

DOI:10.3969/j.issn.1003-3998.2017.06.007     

Shao G M , Chai X J .

Approximation of the incompressible Navier-Stokes-Fourier system by the artificial compressibility method

Acta Math Sci, 2017, 37A (6): 1070- 1084

DOI:10.3969/j.issn.1003-3998.2017.06.007     

Ma W X .

Complexiton solutions to the Korteweg-de Vries equation

Phys Lett A, 2002, 301 (1): 35- 44

URL    

Zhang J B , Ma W X .

Mixed lump-kink solutions to the BKP equation

Comput Math Appl, 2017, 74: 591- 596

DOI:10.1016/j.camwa.2017.05.010     

Zhao H Q , Ma W X .

Mixed lump-kink solutions to the KP equation

Comput Math Appl, 2017, 74: 1399- 1405

DOI:10.1016/j.camwa.2017.06.034     

陈林.

一类拟线性Kirchhoff型椭圆方程组多解的存在性

数学物理学报, 2017, 37A (4): 671- 683

URL    

Chen L .

Multiple solutions for a quasilinear elliptic system of Kirchhoff type

Acta Math Sci, 2017, 37A (4): 671- 683

URL    

Ma W X , Yong X , Zhang H Q .

Diversity of interaction solutions to the (2+1)-dimensional Ito equation

Comput Math Appl, 2017, 75: 289- 295

魏含玉, 夏铁成.

广义Broer-Kaup-Kupershmidt孤子方程的拟周期解

数学物理学报, 2016, 36A (2): 317- 327

URL    

Wei H Y , Xia T C .

Quasi-periodic solution of the generalized Broer-Kaup-Kupershmidt soliton equation

Acta Math Sci, 2016, 36A (2): 317- 327

URL    

Fan E , Zhang H .

A note on the homogeneous balance method

Phys Lett A, 1998, 246: 403- 406

DOI:10.1016/S0375-9601(98)00547-7     

Fan E .

Two new applications of the homogeneous balance method

Phys Lett A, 2000, 265: 353- 357

DOI:10.1016/S0375-9601(00)00010-4     

Senthilvelan M .

On the extended applications of homogeneous balance method

Appl Math Comput, 2001, 123: 381- 388

URL    

Zhang S .

The periodic wave solutions for the (2+1) dimensional Konopelchenko-Dubrovsky equations

Chaos Soliton Fract, 2006, 30: 1213- 1220

DOI:10.1016/j.chaos.2005.08.201     

El-Sabbagh M F , Ali A T .

Nonclassical symmetries for nonlinear partial differential equations via compatibility

Commun Theor Phys, 2011, 56: 611- 616

DOI:10.1088/0253-6102/56/4/02     

Liu J G , Zhou L , He Y .

Multiple soliton solutions for the new (2+1)-dimensional Korteweg-de Vries equation by multiple exp-function method

Appl Math Lett, 2018, 80: 71- 78

DOI:10.1016/j.aml.2018.01.010     

El-Sabbagh M F , Ali A T , El-Ganaini S .

New abundant exact solutions for the system of (2+1)-dimensional Burgers equations

Appl Math Inform Sci, 2008, 2 (1): 31- 41

URL     [本文引用: 1]

Dai C Q , Wang Y Y , Zhang J F .

Analytical spatiotemporal localizations for the generalized (3+1)-dimensional nonlinear Schrödinger equation

Opt Lett, 2010, 35: 1437- 1439

DOI:10.1364/OL.35.001437     

Zhang S .

A generalized auxiliary equation method and its application to (2+1)-dimensional Korteweg-de Vries equations

Comput Math Appl, 2007, 54: 1028- 1038

DOI:10.1016/j.camwa.2006.12.046     

Wu G C , Xia T C .

Uniformly constructing exact discrete soliton solutions and periodic solutions to differential-difference equations

Comput Math Appl, 2009, 58: 2351- 2354

DOI:10.1016/j.camwa.2009.03.022     

Wang C J , Dai Z D , Mu G , Lin S Q .

New exact periodic solitary-wave solutions for new (2+1)-dimensional KdV equation

Commun Theor Phys, 2009, 52: 862- 864

DOI:10.1088/0253-6102/52/5/21     

Dai Z D , Lin S Q , Fu H M , Zeng X P .

Exact three-wave solutions for the KP equation

Appl Math Comput, 2010, 216 (5): 1599- 1604

URL    

Zeng X P , Dai Z D , Li D L .

New periodic soliton solutions for the (3+1)-dimensional potential-YTSF equation

Chaos Soliton Fract, 2009, 42: 657- 661

DOI:10.1016/j.chaos.2009.01.040     

Dai Z D , Li S L , Dai Q Y , Huang J .

Singular periodic soliton solutions and resonance for the KadomtsevPetviashvili equation

Chaos Soliton Fract, 2007, 34 (4): 1148- 1153

DOI:10.1016/j.chaos.2006.04.028     

Dai Z D , Liu Z J , Li D L .

Exact periodic solitary-wave solution for KdV equation

Chin Phys Lett, 2008, 25 (5): 1151- 1153

URL     [本文引用: 1]

Ablowitz M J , Clarkson P A . Solitons, Nonlinear Evolution Equations and Inverse Scattering Transform. Cambridge: Cambridge University Press, 1990

[本文引用: 1]

Manukure S , Zhou Y , Ma W X .

Lump solutions to a (2+1)-dimensional extended KP equation

Comput Math Appl, 2018, 75 (7): 2414- 2419

DOI:10.1016/j.camwa.2017.12.030      [本文引用: 1]

Ma W X .

Lumps and their interaction solutions of (3+1)-dimensional linear PDEs

J Geom Phys, 2018, 133: 10- 16

DOI:10.1016/j.geomphys.2018.07.003     

Ma W X , Zhou Y .

Lump solutions to nonlinear partial differential equations via Hirota bilinear forms

J Differential Equations, 2018, 264: 2633- 2659

DOI:10.1016/j.jde.2017.10.033     

Chen S T , Ma W X .

Lump solutions to a generalized Bogoyavlensky-Konopelchenko equation

Front Math China, 2018, 13 (3): 525- 534

DOI:10.1007/s11464-018-0694-z     

Ma W X , Zhu Z .

Solving the (3+1)-dimensional generalized KP and BKP equations by the multiple exp-function algorithm

Appl Math Comput, 2012, 218 (24): 11871- 11879

URL     [本文引用: 1]

Xia T C , Li B , Zhang H Q .

New explicit and exact solutions for the Nizhnik-Novikov-Vesselov equationy

Appl Math E-Notes, 2001, 1: 139- 142

URL     [本文引用: 1]

Tang Y N , Zai W J .

New exact periodic solitary-wave solutions for the (3+1)-dimensional generalized KP and BKP equations

Comput Math Appl, 2015, 70 (10): 2432- 2441

DOI:10.1016/j.camwa.2015.09.017      [本文引用: 2]

Ma W X , Fan E G .

Linear superposition principle applying to Hirota bilinear equations

Comput Math Appl, 2011, 61: 950- 959

DOI:10.1016/j.camwa.2010.12.043      [本文引用: 2]

Ma W X , Abdeljabbar A .

A bilinear bäcklund transformation of a (3+1)-dimensional generalized KP equation

Appl Math Lett, 2012, 25 (10): 1500- 1504

DOI:10.1016/j.aml.2012.01.003      [本文引用: 1]

Peng W Q , Tian S F , Zhang T T .

Analysis on lump, lumpoff and rogue waves with predictability to the (2+1)-dimensional B-type Kadomtsev-Petviashvili equation

Phys Lett A, 2018, 382 (38): 2701- 2708

DOI:10.1016/j.physleta.2018.08.002      [本文引用: 1]

Qin C Y , Tian S F , Wang X B , et al.

Rogue waves, bright-dark solitons and traveling wave solutions of the (3+1)-dimensional generalized Kadomtsev-Petviashvili equation

Comput Math Appl, 2018, 75 (12): 4221- 4231

DOI:10.1016/j.camwa.2018.03.024     

Tu J M , Tian S F , Xu M J , et al.

Bäcklund transformation, rogue wave solutions and interaction phenomena for a (3+1)-dimensional B-type Kadomtsev-Petviashvili-Boussinesq equation

Nonlinear Dyn, 2018, 92 (2): 709- 720

DOI:10.1007/s11071-018-4085-5     

Wang X B , Tian S F , Qin C Y , Zhang T T .

Characteristics of the solitary waves and rogue waves with interaction phenomena in a generalized (3+1)-dimensional Kadomtsev-Petviashvili equation

Appl Math Lett, 2017, 72: 58- 64

DOI:10.1016/j.aml.2017.04.009     

Wang X B , Tian S F , Yan H , Zhang T T .

On the solitary waves, breather waves and rogue waves to a generalized (3+1)-dimensional Kadomtsev-Petviashvili equation

Comput Math Appl, 2017, 74 (3): 556- 563

DOI:10.1016/j.camwa.2017.04.034     

Tu J M , Tian S F , Xu M J , Ma P L .

waves, solitary waves and asymptotic properties for a generalized (3+1)-dimensional variable-coefficient B-type Kadomtsev-Petviashvili equation

Nonlinear Dyn, 2017, 88 (3): 2265- 2279

DOI:10.1007/s11071-017-3375-7      [本文引用: 1]

Feng L L , Tian S F , Wang X B , Zhang T T .

Rogue waves, homoclinic breather waves and soliton waves for the (2+1)-dimensional B-type Kadomtsev-Petviashvili equation

Appl Math Lett, 2017, 65: 90- 97

DOI:10.1016/j.aml.2016.10.009     

Tu J M , Tian S F , Xu M J , et al.

On periodic wave solutions with asymptotic behaviors to a (3+1)-dimensional generalized B-type Kadomtsev-Petviashvili equation in fluid dynamics

Comput Math Appl, 2016, 72 (9): 2486- 2504

DOI:10.1016/j.camwa.2016.09.003     

Tian S F , Zhang H Q .

On the integrability of a generalized variable-coefficient Kadomtsev-Petviashvili equation

J Phys A:Math Theor, 2012, 45 (5): 055203

DOI:10.1088/1751-8113/45/5/055203     

Wang X B , Tian S F , Feng L L , Zhang T T .

On quasi-periodic waves and rogue waves to the (4+1)-dimensional nonlinear Fokas equation

J Math Phys, 2018, 59 (7): 073505

DOI:10.1063/1.5046691     

Wang X B , Tian S F , Xu M J , Zhang T T .

On integrability and quasi-periodic wave solutions to a (3+1)-dimensional generalized KdV-like model equation

Appl Math Comput, 2016, 283: 216- 233

URL    

Tu J M , Tian S F , Xu M J , et al.

Bäcklund transformation, infinite conservation laws and periodic wave solutions of a generalized (3+1)-dimensional nonlinear wave in liquid with gas bubbles

Nonlinear Dyn, 2016, 83 (3): 1199- 1215

DOI:10.1007/s11071-015-2397-2     

Xu M J , Tian S F , Tu J M , Zhang T T .

Bäcklund transformation, infinite conservation laws and periodic wave solutions to a generalized (2+1)-dimensional Boussinesq equation

Nonlinear Anal-Real, 2016, 31: 388- 408

DOI:10.1016/j.nonrwa.2016.01.019     

Tu J M , Tian S F , Xu M J , Zhang T T .

Quasi-periodic waves and solitary waves to a generalized KdVCaudrey-Dodd-Gibbon equation from fluid dynamics

Taiwanese J Math, 2016, 20 (4): 823- 848

DOI:10.11650/tjm.20.2016.6850     

Xu M J , Tian S F , Tu J M , et al.

On quasiperiodic wave solutions and integrability to a generalized (2+1)-dimensional Korteweg-de Vries equation

Nonlinear Dyn, 2016, 82 (4): 2031- 2049

URL    

Tian S F , Zhang H Q .

On the integrability of a generalized variable-coefficient forced Korteweg-de Vries equation in fluids

Stud Appl Math, 2014, 132 (3): 212- 246

DOI:10.1111/sapm.12026      [本文引用: 1]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发