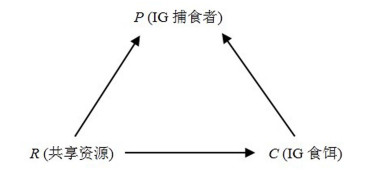
1 引言
共位群内捕食(Intraguild predation,简称IGP)是指在同营养级别的物种间既有竞争关系又存在捕食关系.共位群内捕食(IGP)是生态系统中普遍存在的一种种群之间的关系,它通常发生在吃相同食物但体型不同的生物之间,大量存在于淡水、海水、陆地食物网以及寄生物与病原体关系中.例如,在淡水水域中,蓝鳃太阳鱼与昆虫共同捕食浮游生物,同时蓝鳃太阳鱼又以昆虫为食;在沙漠中,蜘蛛与蝎子共同以昆虫为食,从而蜘蛛与蝎子为捕食昆虫而存在竞争,但两者之间又存在捕食与被捕食关系.由于IGP系统广泛存在于捕食性动物群落里, IGP在群落营养结构中发挥着重要作用,对群落结构有深刻的影响,例如IGP会产生生态位的分离,种群间的相互排斥,改变原有的食物链串联结构,对资源有间接的正作用等等,因此IGP的研究对于揭示生态系统同一营养层的不同物种之间的作用关系和种群演替规律具有比较重要的意义.
图 1
近年来, IGP模型复杂动力学行为的研究备受关注,并且已有众多学者对其进行了大量的研究分析. Hsu等[5]将一般IGP模型中的所有功能性反应函数均选取为Holling-Ⅰ型,对其进行分析,研究结果表明系统会出现振荡和混沌现象. Kang和Wedekin[6]建立了一类IGP模型,在模型中, IG食饵和IG捕食者对共享资源的相互作用关系选取Holling-Ⅰ型功能性反应函数,而IG食饵与IG捕食者之间的相互作用关系选取Holling-Ⅲ型功能性反应函数,并证明了系统存在多重内部平衡点以及多重复杂吸引子.本文主要在文献[5-6]的基础上,建立具有Holling-Ⅱ型功能性反应函数的共位群内捕食模型,并进一步研究其复杂的动力学性态.
其中
本文的主要目的是研究系统(2.1)的动力学性态.在第2节中,简化系统(1.1)并给出系统(2.1)边界平衡点的存在性条件,研究了边界平衡点的局部稳定性.由于系统较为复杂,对其进行理论分析存在一定难度,因此在第3节中我们选取适当的参数对系统进行数值仿真,并进一步研究模型的复杂动力学性态,仿真结果表明系统在一定参数条件下无正平衡点,但在
2 边界平衡点的存在性及稳定性
为了研究方便,首先将系统(1.1)进行无量纲化.令
则系统(1.1)可简化为
下面我们主要研究系统(2.1)的复杂动力学性态.通过直接计算可得,系统(2.1)始终存在两个边界平衡点
进一步分析可知
(1)当
(2)当
下面给出本节的主要结论.
定理2.1 (ⅰ)系统(2.1)始终存在平衡点
(ⅱ)系统(2.1)始终存在平衡点
(ⅲ)当
以及
则
或
则
(ⅳ)当
以及
则
或
则
证 对于系统(2.1),当
(ⅰ)在平衡点
直接计算可得,矩阵
又因为坐标平面
(ⅱ)在平衡点
由计算可得
因此,如果
(ⅲ)当
存在,其对应的系统(2.1)的线性化矩阵为
计算可得
其中
以及
即
或
即
(ⅳ)证明思路及过程与情形(ⅲ)相同,故在此省略.
3 数值仿真
选取系统(2.1)中的参数如下
验证可知,参数满足不等式
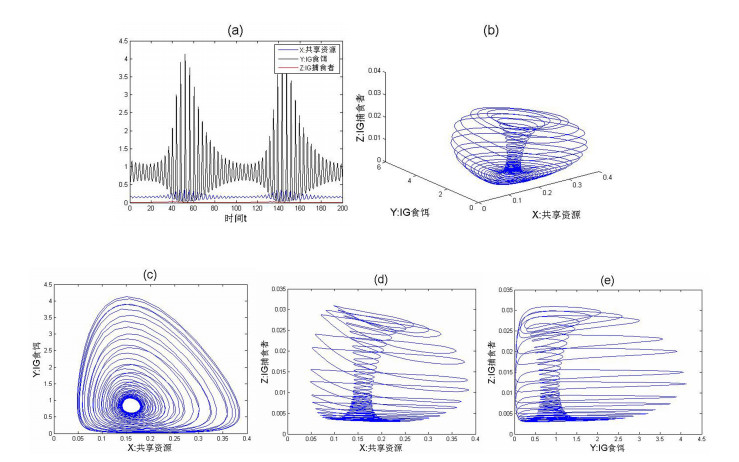
图 2
图 2
选定参数(*),初值为
(a)
为了能更清楚的了解不变环面上的性态,我们通过Poincaré映射,将图 2(b)上连续运动的轨迹用Poincaré截面将其横截,从而根据轨迹在截面上穿过的情况来判断其动力学性态.
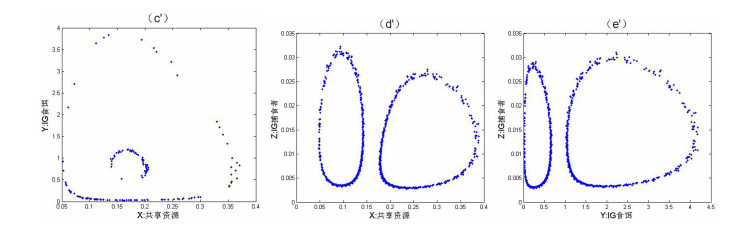
图 3
图 3
选定参数(*),初值为
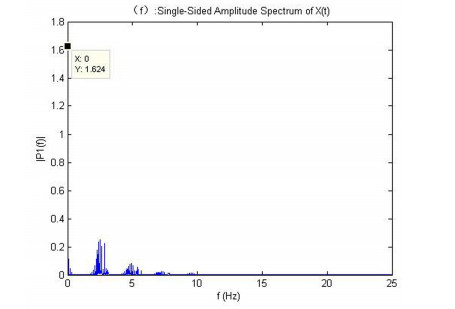
(
图 4
4 总结
本文研究了一类具有Holling-Ⅱ型功能性反应函数的共位群内捕食系统.通过计算给出了系统(2.1)边界平衡点存在的条件,并研究了边界平衡点的局部稳定性.选取系统(2.1)的参数(*),此时参数满足
本文仅指出,在一定参数条件下,系统(2.1)存在吸引的不变环面.但是,不变环面以及平衡点
参考文献
Intraguild predation:the dynamic of complex trophic interaction
DOI:10.1016/0169-5347(92)90208-S [本文引用: 2]
A theoertical framework for intraguild predation
Analysis of the three Lotka-Volterra food web models with omnivory
DOI:10.1016/j.jmaa.2015.01.035 [本文引用: 2]
Dynamics of a intraguild predation model with generalist or specialist predator
DOI:10.1007/s00285-012-0584-z [本文引用: 3]