1 引言
近年来,随着人类社会高速发展,生态问题日益突出,环境污染、物种灭绝引起了人们的高度重视,进而催生了种群生态学的快速发展.其中运用数学模型分析种群变化规律是生态学中重要的一个方法.人们最关心的问题是如何维持种群数量的合理、保持生态系统的稳定,而在数学上,这类问题就是关于竞争模型解的稳定性问题.本文对三种群的Lotka-Volterra竞争模型进行了分析.
Lotka-Volterra捕食者-食饵模型最初是由Lotka于1910年在自催化反应理论[1-4]中提出. 1926年数学家和物理学家Volterra提出了同样的方程组[5-6],并用它解释一战期间亚得里亚海掠食性鱼类数量与渔捞量之间的关系[7].由于种群竞争模型分别由Lotka和Volterra两人提出,因此后来称之为Lotka-Volterra模型. Lotka-Volterra模型被用来解释捕食者和被捕食者的自然种群的动态,例如哈德逊湾公司的山猫和雪兔的数量[8]、罗亚岛国家公园里的鹿群和狼群数量[9].该模型为研究种群竞争关系提供了理论基础,并对现代生态学理论的发展产生了重要影响.基于该模型的基本概念和理论框架,人们进行了一些改进和实践研究[10-13].徐瑞等人[14]研究了一类具有时滞和基于比率的三种群Lotka-Volterra模型.证明了该系统在适当条件下的一致持久性,并通过构造李亚普诺夫函数的方法,得到了使该系统正平衡点全局渐近稳定的充分条件.陆忠华等人[15]研究了既有捕食关系又有竟争关系的三种群Lotka-Volterra模型,从周期系数的观点出发,得到了全局渐近稳定周期解的唯一存在条件.伏升茂等人[16]研究了具有自扩散和互扩散的三种群Lotka-Volterra模型,从自扩散和交叉扩散的角度讨论了一致有界解的全局存在性,证明了正平衡点的全局渐近稳定性.在竞争模型中,物种的持久性和灭绝与物种的初始数量有关,而分形理论中的Julia集与初始点的轨迹相关,这为我们研究Lotka-Volterra模型提供了一种新思路.据我们所知,目前为止运用分形理论讨论Lotka-Volterra模型尚未少数,因此本文从分形的角度对竞争模型进行了研究.
目前为止运用Julia集研究种群竞争模型主要集中在二维生态系统[20].但是生物界中大量存在着三维甚至更高维数的种群竞争,如狮子与斑马、水牛,雕与绵羊、鹿.因此本文将Julia集引入三种群捕食-食饵模型进行讨论.在三种群捕食-食饵模型中,
本文首先介绍了种群竞争模型的Julia集,讨论了初始种群数对模型的影响.然后采用辅助参考反馈控制方法对模型的Julia集进行了控制,实现了模型由不稳定向稳定的转换,同时讨论了当一个种群初始数量变化时,另外两个种群相应的变化.最后通过引入耦合控制项,实现两个参数不同的系统之间的同步. MATLAB仿真证明了控制的有效性.
2 所用到的分形Julia集的部分性质
设
假设
定义2.1 设
用
(ⅰ)
(ⅱ)
(ⅲ)对任何正整数
(ⅳ)
3 三种群竞争模型的Julia集
本文研究了以下三种物种竞争模型
根据欧拉离散方法,取步长为1,可得下列离散方程
其中,
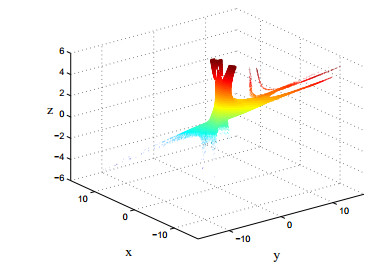
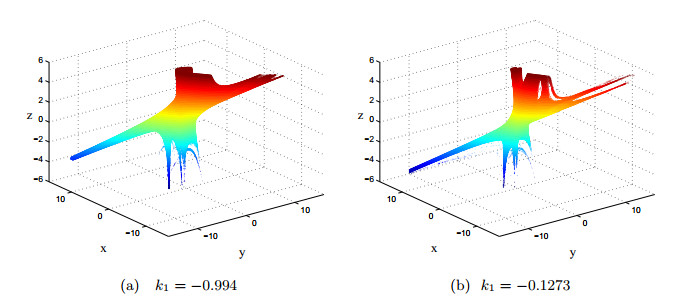
图 1
设该系统的不动点
其解分为以下几种情况
(1)
(2)
(3)
(4)
系统(3.2)在
令
其中
为了方便表示,令
则(3.4)式变为
可以用Matlab求得上式解,由于解的形式过于复杂,这里就不展开写了,以
4 竞争模型Julia集的控制
系统的稳定性在生态系统的分析中起着重要的作用,稳定的生态系统对于保持完整的系统功能是非常重要的.近年来随着工业的发展,生态平衡受到严重破坏,为了保持生态系统稳定,人为地对生态系统进行控制是十分重要的.我们可以根据客观问题的实际需要,通过设计控制系统,消除有害因素,引入有用的控制,有效地约束描述系统初始个数的Julia集,达到控制的效果.
将线性反馈控制器引入到系统(3.2)中,得到被控系统如下
其中
因此,辅助参考项
系统(4.2)在
令
其中
为了方便表示,令
则(4.3)式变为
由于解的形式的复杂性,以
由于
其中
根据Jury判据
上述条件满足,故系统是稳定的.
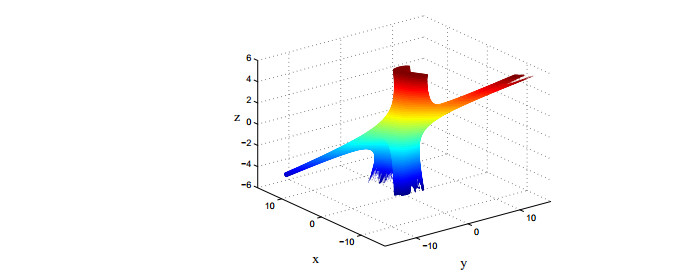
对应的分形图如图 2.通过调整反馈控制参数
图 2
图 2
当
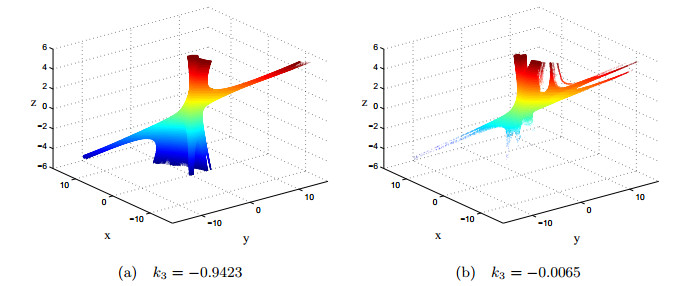
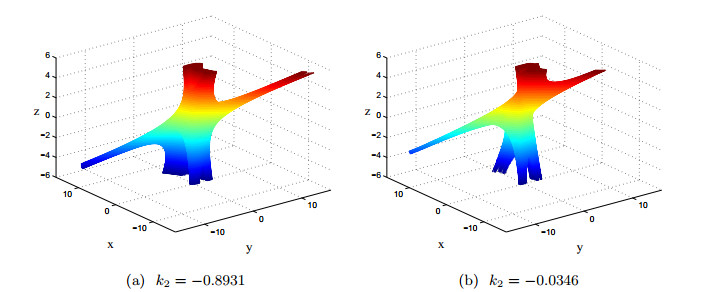
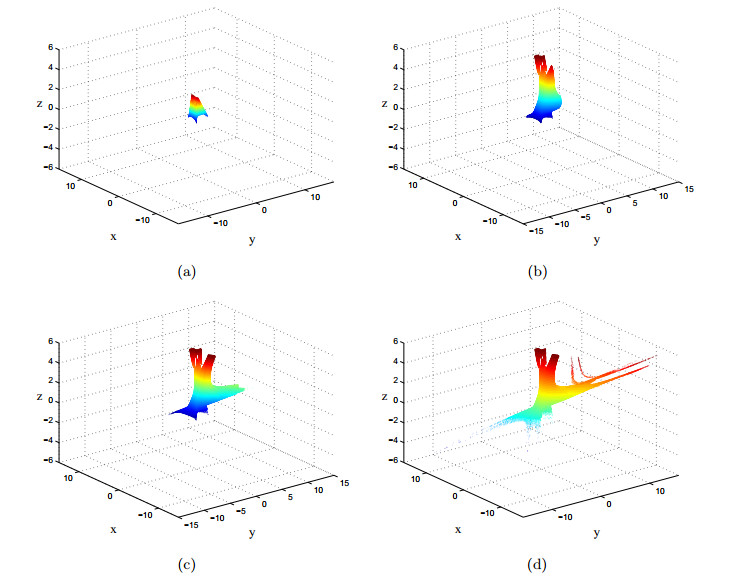
同时,我们可以控制单一变量,观察某一种群的数量变化对另外两个种群以及整个生态系统的影响.保持
图 3
图 4
图 5
5 竞争模型Julia集的同步
众所周知,非线性动力系统的同步是一个重要而有趣的研究课题,它广泛应用于力学、通信等领域,人们对此进行研究并取得了很多成果.在这一节中,我们将讨论两种形式相同但参数不同的的Julia集的同步问题.根据Julia集的定义,一旦给出了系统的参数,其相应的Julia集就是确定的和唯一的,并且它们之间没有相关性.通过引入非线性耦合控制项,使得系统(3.2)变成另一个系统,实现两个系统的耦合.
考虑与系统(3.2)形式相同但参数不同的系统
为了实现系统(3.2)与系统(5.1)的同步,引入非线性耦合控制项,得到耦合系统如下
定理5.1 当
证 由于Julia集以及系统参数的有界性,存在
当
证毕.
定理5.2 当
证 由于Julia集以及系统参数的有界性,存在
易知,当
根据Julia集的定义和上述定理,耦合控制系统(5.1)的Julia集变为系统(3.2)的Julia集,从而实现系统(3.2)和系统(5.1)的Julia集的同步.虽然在给定参数时确定了Julia集,但通过采用不同的耦合参数,我们可以看到Julia集的变化过程.图 1是系统(3.2)中参数取
图 6
图 6
系统(5.1)的Julia集随着耦合控制项的变化,最终实现同步.
(a)响应系统. (b)
6 结论
种群竞争模型不仅是理论研究的重要模型,更是实际应用的重要模型,模型的原始数量对种群数量的长期变化具有重要意义,因此可以用于指导生态、研究种群发展.与传统的李雅普诺夫分析方法相对比,分形方法使用更加直观、方便.李雅普诺夫方法是运用李氏判据处理稳定性问题,其关键步骤是构造李雅普诺夫函数
参考文献
Contribution to the theory of periodic reaction
DOI:10.1021/j150111a004 [本文引用: 1]
On the volterra and other nonlinear models of interacting populations
Analytical note on certain rhythmic relations in organic systems
Variazione e fluttuazioni de numero d'individui in specie animali conviventi
Variations and fluctuations of the number of individuals in animal species living together
Modeling nature:episodes in the history of population ecology, by Sharon E. Kingsland
Do hares eat lynx?
The wolves of Isle Royale display scale-invariant satiation and ratio-dependent predation on moose
DOI:10.1111/j.1365-2656.2005.00977.x [本文引用: 1]
On a limiting system in the Lotka-Volterra competition with cross-diffusion
Permanence and persistence of time varying Lotka-Volterra systems
基于生态环境和反馈控制的多种群竞争系统的正周期解
DOI:10.3969/j.issn.1003-3998.2017.03.015
Positive periodic solution of multiple species comptition system with ecological environment and feedback controls
DOI:10.3969/j.issn.1003-3998.2017.03.015
Complex dynamics of Holling type Ⅱ Lotka-Volterra predator-prey system with impulsive perturbations on the predator
具有时滞和基于比率的三种群捕食系统的持久性与全局渐近稳定性
DOI:10.3969/j.issn.1000-0577.2001.02.010 [本文引用: 1]
Persistence and global stability for three-species ratio-dependent predator-prey system with time delays
DOI:10.3969/j.issn.1000-0577.2001.02.010 [本文引用: 1]
Analysis of the periodic Lotka-Volterra three-species mixed model
Uniform boundedness and stability of solutions to the threespecies Lotka-Volterra competition model with self and cross-diffusion
A Julia set model of field-directed morphogenesis:developmental biology and artificial life
Image compression and encryption scheme using fractal dictionary and Julia set
DOI:10.1049/iet-ipr.2014.0224 [本文引用: 1]
Julia set describes quantum tunnelling in the presence of chaos
DOI:10.1088/0305-4470/35/17/101 [本文引用: 1]
Fractal analysis and control in the predator-prey model
DOI:10.1080/00207160.2015.1130825 [本文引用: 1]