1 引言
双曲型方程在自然科学领域有着广泛的应用背景,它反映了自然界中的振动和波动现象,比较典型的有描述弦振动的一维波动方程,以及描述声波及电磁波传播现象的方程等.我们考虑一类带小参数的二阶双曲型初边值问题
其中
求解双曲型方程的有限差分法方法已有很多[1],但这些格式一般都是基于均匀网格构造的.当问题(1.1)中参数
2 有限差分格式
本节我们构造空间移动网格上模型方程(1.1)的差分格式.设空间和时间剖分数分别为
该格式在均匀网格上是无条件稳定的,精度为
令
我们可将格式(2.1)化简为
对于初始条件和边界条件
消去
由
3 自适应网格的生成和解的更新
设
我们可求得网格映射
的离散形式求得.式中
离散网格方程(3.1),我们使用Gauss-Seidel方法来实现旧网格
从而可得新网格的计算公式
具体计算中我们通过(3.4)式不断迭代生成新网格,直至相邻两次生成的网格之间没有明显的变化时停止迭代.即给定一个误差控制量
新网格产生后,定义在旧网格上的离散解不能和新网格单元一一对应了,我们需要对新网格点上的解进行更新.我们通过以下的守恒型插值格式来获取新网格上对应的数值解.假定新网格
记网格移动量为
这里忽略了高阶项,
由插值公式(3.7),新网格上的数值解可由
求得,其中
4 算法和数值实验
根据自适应网格的生成方法和网格迭代过程中解重新分布的方法,我们给出移动网格方法求解模型方程(1.1)的算法.具体的步骤如下.
第一步 给定求解区域
第二步 在上一步产生的自适应网格上求解模型问题(1.1),利用差分格式(2.2),由已有的
第三步 用
第四步 如果
下面我们根据上述算法来进行数值实验.
例4.1
这里
表 1–4列出了
表 1
移动网格上求解的
| 9.508E-05 | 2.797E-04 | 5.684E-04 | 9.174E-04 | |||||
| 2.530E-05 | 1.91 | 8.225E-05 | 1.77 | 1.684E-04 | 1.76 | 2.673E-04 | 1.78 | |
| 8.934E-06 | 1.50 | 2.225E-05 | 1.89 | 4.630E-05 | 1.86 | 7.321E-05 | 1.87 |
表 2
移动网格上求解的最大模误差(
| 1.952E-04 | 7.678E-04 | 1.480E-03 | 2.196E-03 | |||||
| 5.472E-05 | 1.83 | 2.433E-04 | 1.66 | 4.720E-04 | 1.65 | 6.970E-04 | 1.66 | |
| 2.099E-05 | 1.38 | 6.838E-05 | 1.83 | 1.354E-04 | 1.80 | 1.999E-04 | 1.80 |
表 3
均匀网格上求解的
| 7.683E-04 | 2.571E-03 | 4.787E-03 | 6.949E-03 | |
| 3.513E-04 | 1.113E-03 | 1.902E-03 | 2.499E-03 | |
| 1.127E-04 | 3.276E-04 | 5.221E-04 | 6.652E-04 |
表 4
均匀网格上求解的最大模误差(
| 5.433E-03 | 1.813E-02 | 3.353E-02 | 4.808E-02 | |
| 3.256E-03 | 1.001E-02 | 1.596E-02 | 1.834E-02 | |
| 1.201E-03 | 2.842E-03 | 4.560E-03 | 5.417E-03 |
表 5
移动网格上求解的
| 1.622E-04 | 2.400E-04 | 4.571E-04 | 6.861E-04 | |||||
| 4.274E-05 | 1.92 | 5.581E-05 | 2.10 | 1.147E-04 | 1.99 | 1.750E-04 | 1.97 | |
| 1.948E-05 | 1.13 | 1.698E-05 | 1.72 | 2.800E-05 | 2.03 | 4.703E-05 | 1.90 |
表 6
移动网格上求解的最大模误差(
| 1.952E-04 | 7.678E-04 | 1.480E-03 | 2.196E-03 | |||||
| 5.472E-05 | 1.83 | 2.433E-04 | 1.66 | 4.720E-04 | 1.65 | 6.970E-04 | 1.66 | |
| 2.099E-05 | 1.38 | 6.838E-05 | 1.83 | 1.354E-04 | 1.80 | 1.999E-04 | 1.80 |
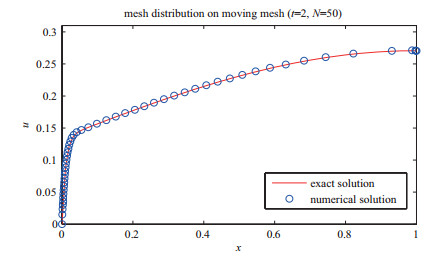
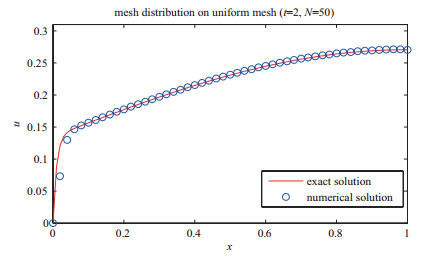
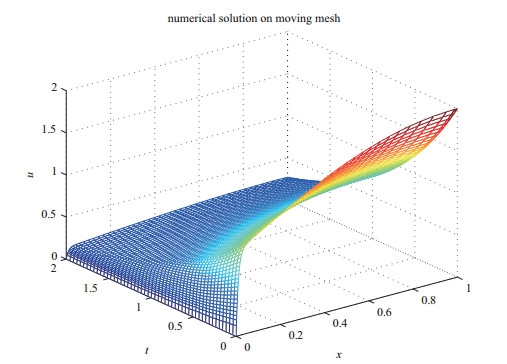
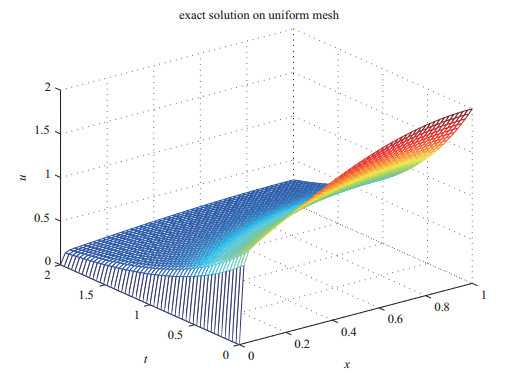
图 1-图 3给出了
图 1
图 2
图 3
图 4
图 5
图 6
5 结语
本文针对一类二阶双曲型方程提出了自适应移动网格方法,该方法对不同时间层的空间区域采用自适应移动网格获取数值解.我们通过数值实验说明了对于解在局部存在急剧变化的二阶双曲型问题,在移动网格上求解比均匀网格上求解具有更好的逼近效果.该方法可以推广到高维的情形.
参考文献
基于移动网格的熵稳定格式
DOI:10.3969/j.issn.1001-246X.2017.02.007 [本文引用: 1]
Entropy stable scheme based on moving meshes for hyperbolic conservation laws
DOI:10.3969/j.issn.1001-246X.2017.02.007 [本文引用: 1]
Moving mesh methods with locally varying time steps
DOI:10.1016/j.jcp.2004.04.007 [本文引用: 2]
Adaptive mesh methods for one-and two-dimensional hyperbolic conservation laws
DOI:10.1137/S003614290138437X [本文引用: 2]
一类奇异摄动对流扩散方程组的自适应移动网格方法
An adaptive moving grid method for the singularly perturbed convection-diffusion problem
Two improved algorithms and implementation for a singularly perturbed problem on moving meshes
DOI:10.1007/s11424-011-8138-9 [本文引用: 1]
An adaptive moving mesh method for thin film flow equations with surface tension
An adaptive mesh redistribution algorithm for convection-dominated problems
A Study on Moving Mesh Finite Element Solution of the Porous Medium Equation
Moving Finite Element Simulations for Reaction-Diffusion Systems
The adaptive time step method for solving phase field crystal model
An adaptive time-stepping strategy for the Cahn-Hilliard equation
DOI:10.4208/cicp.300810.140411s
An adaptive time-stepping strategy for the molecular beam epitaxy models
DOI:10.1137/100812781 [本文引用: 1]