1 引言
同一组数据,采用不同的模型或者同一模型选择不同的算法进行参数估计,得到的估计值可能不一致,因此算法评估问题在数据分析中备受关注,评估指标也变得越发重要,常用指标有简单性、鲁棒性、计算速度以及准确度.简单性亦称可行性,通俗地讲,直观表达各属性在预测中的重要性;鲁棒性是控制系统在一定的参数扰动下,维持某些性能的特性;计算速度代表一个算法的运算量;准确度指估计值与真实值之间的接近程度.算法评估的首要指标是准确度,而衡量“准”的标准至关重要.残差在模型验证和回归分析中起着关键作用[2], Shi等[11]提出以残差信息准则(RIC)作为选择标准,此标准取决于残差方差的估计,如果噪声很大,有效尾分布没有有界二阶矩,此时无法估计方差残差, Tan等[12]采用基于残差最大信息系数的方法,可以有效的拟合数据.
分辨率是衡量准确度的有效指标,并且在很多地方具有不可忽视的作用,例如,敏感参数的测量:假如已知非线性高斯的相对误差是0.01,通过拟合得到的值是0.001,此时模型选择不准,或者拟合值1.01与0.99是否准?有效精度的度量:估计到小数点后5位与后10位是否有区别?准确度的衡量:如果能够得知算法的分辨率,则可以对算法的准确度给出有效评价.分辨率的概念很早已被提出,如时间分辨率是时态特征划分的最小单元,将连续过程离散化的最小时间间隔, min、s、ms等可以定义时间.空间分辨率是图像中能够辨别临界距离的最小极限, m、um、nm等可以定义空间.此外,分辨率在遥感以及CT处理等方面得到广泛应用.参数分辨率的引入,为衡量算法准确度提供了有效手段.由于不同参数或者同一参数其分辨率可能不同,因此需要研究局部分辨率和整体分辨率.
EM(Expectation-maximization)算法又称期望最大化算法, 1977年由Dempster等[4]提出用于求解含有隐变量数学模型的参数极大似然估计,其基本思想:给定不完全数据初始值情形下,估计出模型参数值;然后再根据参数值估计出缺失数据的值,根据估计出的缺失数据的值再对参数值进行更新,反复迭代直至收敛.自Dempster等人提出EM算法以来,国内外取得了很多研究成果,如Wu和Xu[13, 15]总结出EM算法的一些收敛性质. Wei和Liu[7, 14]提出了改进E步、M步.后来许多学者引入加速算法[1, 5-6, 16-17]研究高维EM算法的迭代性能.正态分布因具有灵活、高效拟合的特点,很多随机现象在足够大样本下都可以用此分布来逼近[10]. EM算法易受初始值影响,不能保证找到全局最优,往往容易陷入局部最优,因此关于初始值设置提出了许多方法, Zhai[18]选取最远点为初始值,易使边界点收敛效果受到影响; Li和Chen[9]使用k-最近邻法删除异常值,然后用k-means来初始化,此估计效果显著优于原始效果.近几年有学者采用基于密度的方法选择初始值,这样可以避免噪声点对参数估计的影响,从而提高迭代结果的稳健性.
从EM算法的相关介绍知,其改进集中于提高收敛速度和稳健性,关于参数分辨率问题,目前没有相关文献涉及.本文以两分量混合模型参数估计的EM算法为例,给出EM算法的参数分辨率的定义(详见2.3节).我们发现,两个方差
2 准备工作
2.1 EM算法的相关原理
用Y表示可被观测的随机变量,
EM算法具体为:第
E步:求关于概率函数
如果随机变量Z是连续型,则
如果随机变量Z是离散型,则
这里
M步:极大化
这样就实现了一次
或
则迭代停止.
2.2 两分量模型EM算法的迭代公式
对于二分量模型
2.3 EM算法的参数分辨率
本文以两分量混合模型参数估计的EM算法为例,给出参数分辨率的定义:对两正态混合模型:
(1)对混合模型进行
(2)采用判别准则,判别每轮估计是否将参数
(3)令
其中
定义2.1 设置阈值
3 实验与分析
EM算法在参数估计中存在随机性,每轮迭代结果可能不同,为了避免这种随机性,首先,在每组模型下循环100轮,得到100组EM算法估计值.其次,分辨率计算时,把运行50次结果进行升序排列,依次去除前三个和后三个数值后取平均值.这样不仅克服了一定的偶然性,而且也提高了EM算法的鲁棒性.除此,考虑到EM算法易受初始值影响,初始值均在真实值的
3.1 相对误差与变异系数的影响分析
固定
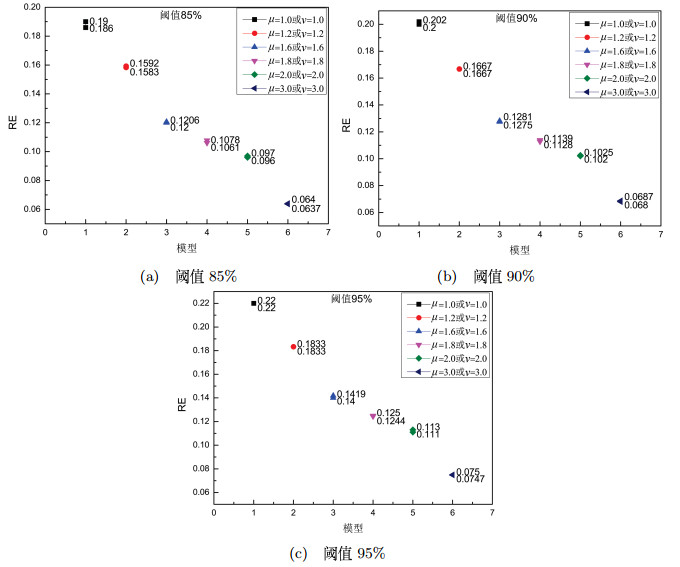
表 1 阈值为85%时的参数分辨率
| 固定 | RE1 | AE1 | 固定 | RE2 | CV1 | CV2 | |
| 0.1900 | 0.190 | 0.1860 | 0.1880 | 0.1840 | 0.2229 | ||
| 0.1592 | 0.191 | 0.1583 | 0.1588 | 0.1552 | 0.1823 | ||
| 0.1200 | 0.192 | 0.1206 | 0.1203 | 0.1183 | 0.1336 | ||
| 0.1061 | 0.191 | 0.1078 | 0.1070 | 0.1058 | 0.1178 | ||
| 0.0960 | 0.192 | 0.0970 | 0.0965 | 0.0956 | 0.1054 | ||
| 0.0640 | 0.192 | 0.0637 | 0.0639 | 0.0647 | 0.0689 |
表 2 阈值为90%时的参数分辨率
| 固定 | RE1 | AE1 | 固定 | RE2 | CV1 | CV2 | |
| 0.2000 | 0.200 | 0.2020 | 0.2010 | 0.1833 | 0.2253 | ||
| 0.1667 | 0.200 | 0.1667 | 0.1667 | 0.1548 | 0.1833 | ||
| 0.1275 | 0.204 | 0.1281 | 0.1278 | 0.1179 | 0.1342 | ||
| 0.1139 | 0.205 | 0.1128 | 0.1134 | 0.1054 | 0.1182 | ||
| 0.1020 | 0.204 | 0.1025 | 0.1023 | 0.0954 | 0.1057 | ||
| 0.0687 | 0.206 | 0.0680 | 0.0684 | 0.0645 | 0.0691 |
表 3
阈值为
| 固定 | RE1 | AE1 | 固定 | RE2 | CV1 | CV2 | |
| 0.2200 | 0.220 | 0.2200 | 0.2200 | 0.1820 | 0.2282 | ||
| 0.1833 | 0.220 | 0.1833 | 0.1833 | 0.1538 | 0.1854 | ||
| 0.1419 | 0.227 | 0.1400 | 0.1410 | 0.1172 | 0.1352 | ||
| 0.1250 | 0.225 | 0.1244 | 0.1247 | 0.1049 | 0.1190 | ||
| 0.1130 | 0.226 | 0.1110 | 0.1120 | 0.0949 | 0.1062 | ||
| 0.0747 | 0.224 | 0.0750 | 0.0749 | 0.0644 | 0.0694 |
阈值设置
图 1
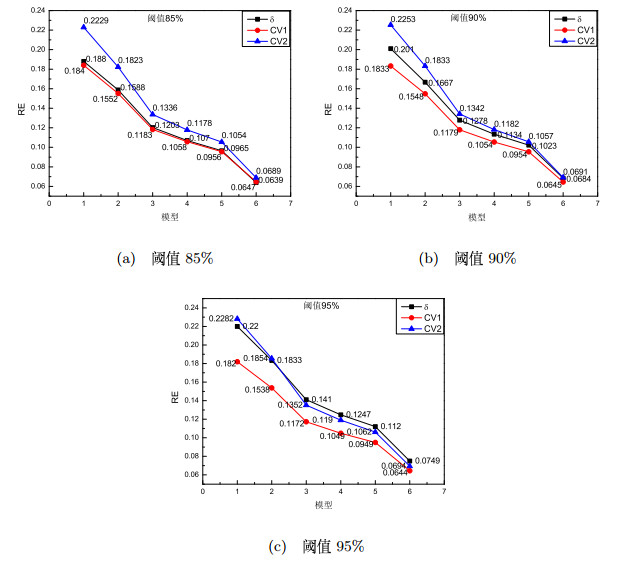
图 2
3.2 相对误差与分辨率的影响分析
基于变异系数影响参数分辨率的计算结果,本小节将进行两方面的研究:一方面将方差依次设置为0.1、0.2、0.3、0.4、0.5,分析方差变化对相对误差的影响,另一方面由EM算法估计出100组参数,利用判别准则(2.1)运行50次后把结果进行升序排名,把最大数值记为极大分辨率、最小数值记为极小分辨率、并依次去除前三个和后三个数值后取平均值得到平均分辨率即整体分辨率,原始模型为
图 3
由图 4可知,当相对误差增大,极值分辨率与整体分辨率均以不减的趋势变化,说明局部分辨率与整体分辨率保持一致;也符合信号越强,相对误差越小的特点.
图 4
3.3 Fisher信任分布的相关理论
基于Fisher的判别准则、混合高斯分布的相关原理以及正态分布密度函数的性质,推导出当
若样本(容量是1),
其中,
从概率的角度知(3.1)和(3.2)式没有实质性的变化.但Fisher赋予(3.2)式信任意义:确定样本X后,将
定理3.1 设随机变量
其中,
证 令
随机变量
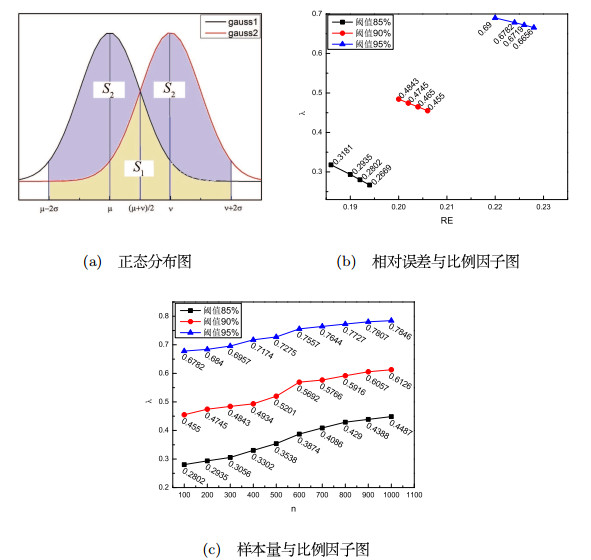
图 5
那么整体区域S的大小(A(S)):
可能误分区域
不可能误分区域
记EM算法参数估计对应的分开区域
故原命题成立.
注3.1 图 5(b)为阈值分别等于
推论3.1 在同一阈值下,当
证 根据实验结果可知,随着样本容量
这里
可知
注3.2 图 5(c)为
4 结论
算法评估指标日益重要,常用的评估指标有简单性、鲁棒性、计算速度及准确度,前三者已取得很多成果,而后者却没有学者研究.由于分辨率是衡量准确度的有效指标,如果可以提前预知分辨率,那么就可以很好的衡量准确度,本文以两分量高斯混合模型为例,给出参数分辨率定义,并运用Fisher思想给出(2.1)式的判别准则,此准则不受随机性和主观因素的影响,进而由(3.2)式推导出(3.3)式两个相近参数分开的信任分布.以两正态混合模型为例进行验证,得到了参数分辨率在EM算法中的可行性.实验表明两个方差为0.1的正态分布其均值距离大于0.206时, EM算法在
参考文献
Acceleration of the EM algorithm:P-EM versus epsilon algorithm
Maximum likelihood from incomplete data via the EM algorithm
Acceleration of the EM algorithm
Accelerating the convergence of the EM algorithm using the vector ε algorithm
The ECME algorithm:A simple extension of EM and ECM with faster monotone convergence
DOI:10.1093/biomet/81.4.633 [本文引用: 1]
Research on Initialization on EM algorithm based on Gaussian mixture model
Regression model selection a residual likelihood approach
DOI:10.1111/rssb.2002.64.issue-2 [本文引用: 1]
Model selection method based on maximal information coefficient of residuals
DOI:10.1016/S0252-9602(14)60031-X [本文引用: 1]
On the convergence properties of the EM algorithm
A Monte Carlo implementation of the EM algorithm and the poor man's data augmentation algorithms
DOI:10.1080/01621459.1990.10474930 [本文引用: 1]
On convergence properties of the EM algorithm for Gaussian mixtures
On convergence and parameter selection of the EM and DA-EM algorithms for Gaussian mixtures
A note on EM algorithm for mixture models