1 引言
广义的(3+1)维Kadomtsev-Petviashvili方程
2 应用拟设方法
2.1 奇异孤子解
拟设
其中
并平衡色散项和非线性项,得
则可得
3 分支相图和定性分析
对方程(1.2)作行波变换
并对
令
对系统(3.3)首次积分可得下面的哈密顿函数
其中
显然,
(ⅰ)若
(ⅱ)若
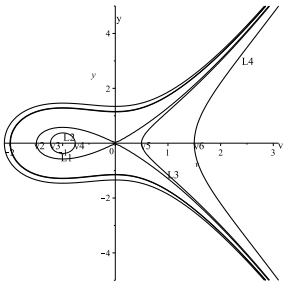
图 1
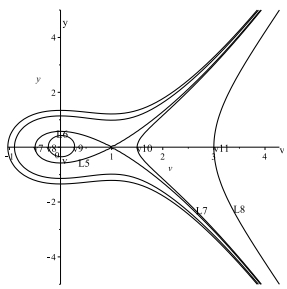
图 2
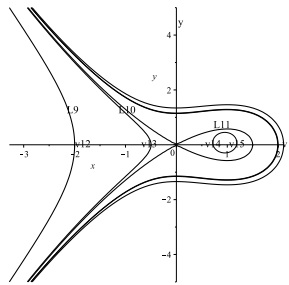
图 3
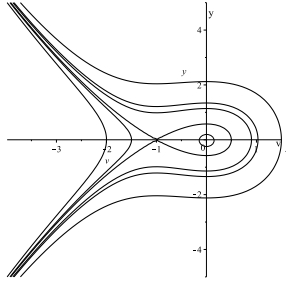
图 4
考虑系统的轨道和哈密顿量
根据以上图,可以得到下面的命题.
命题3.1 当
(ⅰ)当
(ⅱ)当
(ⅲ)当
(ⅳ)当
命题3.2 当
(ⅰ)当
(ⅱ)当
(ⅲ)当
(ⅳ)当
根据动力系统定性理论相关知识,偏微分方程的一个光滑孤立波解对应于一个行波方程的光滑同宿轨,偏微分方程的一个周期波解对应于一个行波方程的光滑周期轨.由以上结论,有下面的命题.
命题3.3 若
(ⅰ)当
(ⅱ)当
(ⅲ)当
命题3.4 若
(ⅰ)当
(ⅱ)当
(ⅲ)当
4 行波解及其联系
首先,研究当
(ⅰ)从分支相图 1,可注意到有一条过鞍点(0, 0)的同宿轨道
其中
把(4.1)式代入系统(3.3)并且沿轨道
完成上面的积分,可得到方程的一个孤立波解和爆破解
(ⅱ)从分支相图 1,可注意到有一条过点
其中
把(4.2)式代入系统(3.3)并且沿轨道
完成上面积分可得如下的周期波解和爆破解
(ⅲ)从分支相图 1,可注意到有一条特殊轨道
其中
完成上面的积分可得如下的周期爆破解
其次,研究当
(ⅰ)从分支相图 2,可注意到有一条过鞍点
其中
完成上面积分,可得如下的孤立波解和爆破波解
(ⅱ)从分支相图 2,可看到过
其中
完成上面的积分可得如下的周期波解和爆破波解
(ⅲ)从分支相图 2,可注意到一条特殊轨道
其中
把(4.6)式代入系统(3.3)并且沿轨道
完成上面的积分可得如下的周期爆破波解
最后,研究当
在分支相图(3)中有一条过
其中
完成上面的积分可得如下的周期波解和爆破波解
当
最后,研究方程行波解之间的联系.
(ⅰ)令
因此,可得
(ⅱ)令
因此,可得
(ⅲ)令
因此,可得
(ⅳ)令
因此,
5 结论
本文利用拟设方法,微分方程定性理论和动力系统分支方法,研究了广义的(3+1)维Kadomtsev-Petviashvili方程的行波解及其相图分支分析.通过行波变换,把方程化为平面系统,画出对应的分支相图,通过分支相图分析轨道,获得了方程的精确行波解.包括奇异孤子解,亮孤子解,拓扑孤子解及其行波解,并研究了行波解之间的联系.
参考文献
Simulation of tapered rotating beams with centrifugal stiffening using the adomian decomposition method
DOI:10.1016/j.apm.2015.09.097 [本文引用: 1]
Adomian decomposition method solution of population balance equations for aggregation, nucleation, growth and breakup processes
Application of adomian decomposition method for micropolor flow in a porous channel
DOI:10.1016/j.jppr.2014.01.004
Numerical solution of the Laplace equation in annulus by Adomian decomposition method
DOI:10.1016/j.chaos.2006.06.016 [本文引用: 1]
Hierarchy of kissing numbers for exceptional Lie symmetry groups in high energy physics
DOI:10.1016/j.chaos.2007.06.121 [本文引用: 1]
Soliton perturbation theory for the generalized klein-gordon equation with full nonlinearity
Lie symmetry methods applied to the turbulent wake of a symmetric self-propelled body
DOI:10.1016/j.apm.2015.10.007 [本文引用: 1]
Singular solitons and bifurcation analysis of quadratic nonlinear klein-gordon equation
Topological and non-topological soliton solutions of the bretherton equation
Bright and dark solitons of the modified complex ginzburg-landau equation with parabolic and dualpower law nonlinearity
Convergence of variational iteration method applied two-point diffusion problems
DOI:10.1016/j.apm.2016.02.024 [本文引用: 1]
Interpolated variational iteration method for initial value problems
A novel fixed point scheme proper setting of variational iteration method for BVPs
DOI:10.1016/j.aml.2015.03.017 [本文引用: 1]
Numerical modeling of the power losses in geared transmissions: Windage, churning and cavitation simulations with a new integrated approach that drastically reduces the computational effort
DOI:10.1016/j.triboint.2016.06.046 [本文引用: 1]
Numerical simulations on the effect of sloshing on liquid flow maldistribution of randomly packed column
DOI:10.1016/j.applthermaleng.2016.10.049
Multi-spatial environmental performance evaluation towards integrated urban design: A procedural approach with computational simulations
DOI:10.1016/j.jclepro.2016.08.151 [本文引用: 1]
On the stability of solitary waves in weakly dispersive media
Soliton deflexion for (1+3)-D Kadomtsev-Petviashvili equation
DOI:10.1016/j.cnsns.2009.02.007 [本文引用: 1]
Are all the equations of the Kadomtsev-Petviashvili hierarchy integrable?
DOI:10.1063/1.527260 [本文引用: 1]
New explicit solutions for(3+1)-dimensional Kadomtsev-Petviashvili (KP) equation
Exact travelling wave solutions to the (3+1)-dimensional Kadomtsev-Petviashvili equation
DOI:10.12693/APhysPolA.108.421 [本文引用: 1]
Application of new generalized
Bifurcation analysis of a diffusive predator-prey system with Crowley-Martin functional response and delay
DOI:10.1016/j.chaos.2016.12.014 [本文引用: 1]
Bifurcation analysis and Turing instability in a diffusive predator-prey model with herd behavior and hyperbolic mortality
DOI:10.1016/j.chaos.2015.10.001 [本文引用: 1]