1 引言
对于此问题的研究与讨论,之前有一些工作.文献[2-3, 6-8]讨论了纯应力边界条件的弹性问题,构造了满足第二类离散Korn不等式的有限元空间,并借助于混合有限元方法分析其收敛性.其中文献[2, 6]构造了三角形单元,文献[3, 7]构造了矩形单元,文献[8]构造了NRQ
本文以弹性纯位移变分问题为基础构造了三维的三棱柱单元并且证明了单元的适定性,得到能量模具有一阶收敛性,
2 基本问题和概念
本文中,
本文讨论的基本问题是均匀介质各向同性材料的纯位移平面弹性问题.令
其中
对应(2.1)变分问题:求
其中
显然由Korn不等式可知任意
由Lax-milgram定理可以得到上述变分问题有唯一解.
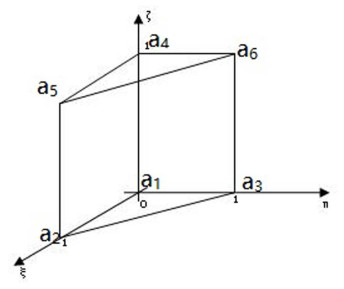
3 三棱柱单元构造
令
令
图 1
在参考单元
其中
则有dim
定理3.1 参考单元上的自由度定义如下
其中
证 三棱柱的五个外表面的方程分别为
由(3.3)式的第(ⅰ)个自由度和形函数空间(3.4)定义,可以得到下面的方程
同理在另外四个面上积分得下面四个方程
同理,对
对(3.4)式定义的多项式求偏导数,得
由(3.2)式定义的形函数空间的约束条件div
计算由(3.5)式, (3.6)和(3.8)式构成的21个方程组成的方程组,可以得到矩阵的阶数也是21,即方程组有唯一解.也即形函数空间(3.2)可以由(3.3)式定义的自由度唯一确定.
定义仿射变换
其中
对向量值函数采用Piola变换
由梯度算子的定义有
定义一般单元
定义插值算子
显然插值算子是仿射等价的.
对于任意
由有限元空间定义可知
引理3.1 插值算子
引理3.2 对于任给
证 由
证毕.
4 误差估计
接下来我们进行误差估计,方程(2.2)对应的离散有限元格式为:求
其中
定义有限元空间
显然当
引理4.1 设
证 由单元
证毕.
引理4.2 定义
证
证毕.
定理4.1 令
证 由Strong引理
首先讨论逼近误差,由于插值对一次多项式精确成立,所以有
再由引理4.1得
由(4.7)-(4.9)式得逼近误差为
这里的常数
接下来讨论相容误差,
设
由(4.11)-(4.13)式得
综合(4.7), (4.10)和(4.14)式,得误差估计(4.6).
接下来我们证明关于位移的
定理4.2 在定理4.1的条件下可得位移的
其中
证 方程(2.1)的对偶问题如下
其中
这里双线性形
对应于(4.17)式的离散问题是求
由定理4.1的证明可知
由
下面我们逐项讨论(4.21)式中各部分.由定理4.1和(4.20)式,有
因为
设
根据位移
类似(4.12)和(4.13)式的分析可以推出
和
由(4.24)-(4.28)式得
和
通过上述逐项分析得到(4.21)-(4.22), (4.28)-(4.30)式,代入
参考文献
Linear finite element methods for planar linear elasticity
DOI:10.1090/S0025-5718-1992-1140646-2 [本文引用: 3]
Nonconforming finite element methods for the equations of linear elasticity
DOI:10.1090/S0025-5718-1991-1094947-6 [本文引用: 2]
New second order nonconforming triangular element for planar elasticity problems
Locking effects in the finite element approximation of elasticity problems
A linear nonconforming finite element method nearly incompressible elasticity and stokes flow
DOI:10.1016/0045-7825(95)00829-P [本文引用: 2]
Analysis of some quadrilateral nonconforming elements for incompressible elasticity
A locking-free nonconforming finite element method for planar linear elasticity
DOI:10.1023/A:1022838628615 [本文引用: 1]
Quadrilateral finite elements for planar linear elasticity problem with large Lamé constant
关于纯位移边界条件的平面弹性问题Locking-Free有限元格式
DOI:10.3321/j.issn:0254-7791.2002.02.011 [本文引用: 2]
On locking-free finite element schemes for the pure displacement boundary value problem in the planar elasticity
DOI:10.3321/j.issn:0254-7791.2002.02.011 [本文引用: 2]
A locking-free scheme of nonconforming rectangular finite element for the planar elasticity
On locking-free finite element schemes for three-dimensional elasticity
A locking-free anisotropic nonconforming finite element for planar linear elasticity problem
A locking-free anisotropic nonconforming rectangular finite element approximation for the planar elasticity problem
DOI:10.1007/s11766-008-0102-7 [本文引用: 1]
一个二阶收敛的平面弹性问题Locking-Free三角形元
DOI:10.3969/j.issn.1005-3085.2009.03.019 [本文引用: 1]
A locking-free triangular element with second-order convergence for the planar elasticity problem
DOI:10.3969/j.issn.1005-3085.2009.03.019 [本文引用: 1]
平面弹性的一个新的Locking-Free非协调有限元
DOI:10.3969/j.issn.1001-9847.2007.04.017 [本文引用: 1]
A new locking-free nonconforming finite element for the planar elasticity
DOI:10.3969/j.issn.1001-9847.2007.04.017 [本文引用: 1]