设$f(z)$与$g(z)$在单位圆盘$U=\{z:|z|<1\}$内解析,如果存在$U$内解析函数$\omega(z)$,且$|\omega(z)|<1, $$\omega(0)=0, $使得$f(z)=g(\omega(z))$,则称$f(z)$从属于$g(z)$,记作$f(z)\prec g(z)$.特别地,如果$g(z)$在$U$上是单叶的,则

$f(z)\prec g(z)\Longleftrightarrow f(0)=g(0), f(U)\subset g(U) (z\in U) .$

用$P$表示在$U$内解析并且满足条件$p(z)\prec\frac{1+z}{1-z}$的所有函数$p(z)=1+\sum\limits_{n=1}^{\infty}p_{n}z^{n}$的全体.

设$S$表示在单位圆盘$U$内单叶解析函数

$f(z)=z+\sum\limits_{n=2}^{\infty}a_nz^n$

构成的函数类. $S^*$, $C$和$B_\alpha$分别表示通常的星象函数类,近于凸函数类和Bazilevič函数类,它们都是$S$的子类且$S^*\subset C\subset B_\alpha$.用$Y$表示圆对称函数(参见文献[1]).

我们用$S_{\lambda}(\psi)$表示如下定义的函数

(1.1)$\begin{equation}\psi(z)=\left[\frac{f(z)}{z}\right]^\lambda=1+\sum\limits_{n=1}^\infty D_n(\lambda)z^n, f(z)\in S, 0<\lambda<1\end{equation}$

的全体组成的函数类.称$\psi(z)$为Milin函数, $ D_n(\lambda)$为Milin系数.

研究Milin系数估计和相邻两系数模之差的模$||D_{n+1}(\lambda)|-|D_n(\lambda)||$是单叶函数论中两个重要问题.对于$f\in S$的形式,还尚未完全解决.

首先,关于Milin系数的估计. Milin^[2]给出了当$\frac{1}{4}<\lambda<1$时, $S$上Milin系数$ |D_n(\lambda)|$准确的阶,但当$0<\lambda\leq\frac{1}{4}$时,只获得了$|D_n(\lambda)|=O(n^{-\frac{1}{2}}\log n)$.邓琴在文献[3]中继续讨论几类特殊单叶函数类($S^*$, $C$, $Y$和$B_\alpha$)上Milin系数$|D_n(\lambda)|$阶的估计,当$0<\lambda<1$时,证明了星象函数$S^*$的Milin系数$|D_n(\lambda)|\leq An^{2\lambda-1}$,近于凸函数$C$的Milin系数$|D_n(\lambda)|\leq An^{2\lambda-1}(\log n)^{\frac{3}{2}}$,圆对称函数$Y$的Milin系数$|D_n(\lambda)|\leq An^{2\lambda-1}\log n$, Bazilevič函数$B_\alpha$的Milin系数$|D_n(\lambda)|\leq An^{2\lambda-1}(\log n)^{\frac{3}{2}}$,阶$2\lambda-1$为最佳值.不同的地方, $A$表示不同常数.

然而我们发现,比$B_\alpha$更广义的函数类上还能否讨论Milin系数问题,这是有待解决的问题.

其次,关于相邻两系数模之差的模估计.记

$||D_{n+1}(\lambda)|-|D_{n}(\lambda)||\leq An^{\frac{b(\lambda)-1}{2}}, \ \ \ n=2, 3, \cdots , $

其中$A$为绝对常数.寻求最佳的$b(\lambda)$是一个有趣的问题.这个问题最初是由Goluzin研究的,并证明了$b(1)=3/2$, $b(1/2)=1/2$,这引起了国内外许多学者的兴趣.随后, Hayman^[4]证明了$b(1)=1$,获得了$\lambda=1$时, $b(\lambda)$的最佳结果.对$1/4<\lambda<1$,胡克^[5]证明了

$||D_{n+1}(\lambda)|-|D_{n}(\lambda)||\leq An^{\frac{b(\lambda)-1}{2}}(\log n)^{\frac{3}{2}}, \ \ \ n=2, 3, \cdots , $

$b(\lambda)=\frac{(4\lambda-1)(2\sqrt{\lambda}-1)^2}{2\lambda+(2\sqrt{\lambda}-1)^2}$,这是目前比较好的结果,但不是最佳结果.当$0<\lambda<1$时, $b(\lambda)$的最佳值是什么呢?此后这个问题虽然屡有进展,但至今尚未解决,仍是一个很值得探讨的问题^[5].

另外,近年来许多学者主要研究单叶函数中一些特殊函数族的相邻系数模之差的估计(参见文献[5-11]).特别地,当$0<\lambda<1$时,邓琴在文献[7]证明了,当$f(z)\in B_\alpha$时, $||D_{n+1}|-|D_{n}||\leq An^{\lambda-1}(\log n)^{\frac{3}{2}}$,阶$\lambda-1$为最佳值.

本文研究如下由杨定恭给出的$\alpha$型$\beta$级Bazilevič函数类^[12].

定义1.1  设$f(z)\in S$, $\alpha\geq0$, $0\leq\beta<1$,若存在$g(z)\in S^*$,使得

(1.2)$\begin{equation} {\rm Re}\left\{\frac{zf'(z)}{f(z)}\left(\frac{f(z)}{g(z)}\right)^\alpha\right\}>\beta, \end{equation}$

则称$f(z)\in B_\alpha(\beta)$.显然$ B_\alpha(0)=B_\alpha$.

杨定恭在文献[12]中给出了$\alpha$型$\beta$级Bazilevič函数类$B_\alpha(\beta)$的Fekete-Szegö不等式.牛潇萌,李书海在文献[13]中给出了$B_\alpha(\beta)$的对数系数.但其Milin系数和相邻两系数模之差的估计还没有研究.本文研究了$\alpha$型$\beta$级Bazilevič函数类$B_\alpha(\beta)$的Milin系数和相邻两系数模之差的估计.解决了以上两个问题,推广了邓琴在文献[3, 7]中的结果,并给出特殊Milin函数的几何刻画.

为了得到$B_\alpha(\beta)$的Milin系数$|D_n(\lambda)|$和相邻两系数模之差,我们需要如下引理.为方便,函数$f(z)$的幂级数展开式中$z^n$系数$a_{n}$表示为$a_{n}=\{f\}_n.$

引理2.1^[10]  设$f(z), g(z)$在$U$内解析, $f(z)\neq 0, g(z)\neq0$,如果$f(z)\prec g(z)$,则对$z=r{\rm e}^{{\rm i}\theta}$, $r<1$,有

(2.1)$\begin{equation}\int_0^{2\pi}\left|\frac{f'(z)}{f(z)}\right|{\rm d}\theta\leq\int_0^{2\pi}\left|\frac{g'(z)}{g(z)}\right|{\rm d}\theta.\end{equation}$

引理2.2^[3]  设$f(z)\in B_\alpha$, $F_1(z)=f(z)^{\lambda-1}f'(z)z^{1-\lambda}$, $0<\lambda<1$,则

(2.2)$\begin{equation}\sum\limits_{m=0}^{n}\left|\{F_1(z)\}_m\right|^2\leq {\cal A}_1n^{4\lambda+1}\log n, \end{equation}$

(2.3)$\begin{equation}\left|\{F_1(z)\}_n\right|\leq {\cal A}_2n^{2\lambda+1}(\log n)^{\frac{1}{2}}, \end{equation}$

(2.4)$\begin{equation}\left|\left\{\frac{zf'(z)}{f(z)}F_1(z)\right\}_n\right|\leq {\cal A}_3n^{2\lambda+1}\log n, \end{equation}$

其中${\cal A}_1, {\cal A}_2, {\cal A}_3$表示绝对常数.

证  由文献[3,定理1]证明过程可知.

引理2.3^[7]  设$f(z)\in B_\alpha$, $G_1(z)=(1-z)f(z)^{\lambda-1}f'(z)z^{1-\lambda}$, $0<\lambda<1$,则对$n\geq2$有

(2.5)$\begin{equation}\sum\limits_{m=0}^{n}\left|\{G_1(z)\}_m\right|^2\leq {\cal B}_1n^{2\lambda+1}\log n, \end{equation}$

(2.6)$\begin{equation}\left|\{G_1(z)\}_n\right|\leq {\cal B}_2n^{\lambda+1}(\log n)^{\frac{1}{2}}, \end{equation}$

(2.7)$\begin{equation}\left|\left\{\frac{zf'(z)}{f(z)}G_1(z)\right\}_n\right|\leq {\cal B}_3n^{\lambda+1}\log n.\end{equation}$

引理2.4  设$f(z)\in B_\alpha(\beta)$, $g(z)\in S^*$满足(1.2)式,令$q(z)=\frac{zf'(z)}{f(z)}\left(\frac{f(z)}{g(z)}\right)^\alpha$, $F_1(z)=f(z)^{\lambda-1}f'(z)z^{1-\lambda}$, $G_1(z)=(1-z)f(z)^{\lambda-1}f'(z)z^{1-\lambda}$, $0<\lambda<1$,则对$z=r{\rm e}^{{\rm i}\theta}$和$\frac{1}{2}\leq r<1$,有

(2.8)$\begin{equation}\left|\left\{\frac{zq'(z)}{q(z)}F_1(z)\right\}_n\right|\leq\frac2{\pi}{\cal A}^{\frac{1}{2}}_1n^{2\lambda+1}\log [n+(1-2\beta)(n-1)] (\log n)^{\frac{1}{2}}, \end{equation}$

(2.9)$\begin{equation}\left|\left\{\frac{zq'(z)}{q(z)}G_1(z)\right\}_n\right|\leq\frac2{\pi}{\cal B}^{\frac{1}{2}}_1n^{\lambda+1}\log [n+(1-2\beta)(n-1)] (\log n)^{\frac{1}{2}}, \end{equation}$

(2.10)$\begin{equation}\left|\left\{\frac{z}{1-z}G_1(z)\right\}_n\right|\leq {\cal B}_1^{\frac12}n^{\lambda+1}(\log n)^{\frac12}.\end{equation}$

证  设$f(z)\in B_\alpha(\beta)$,则存在$g(z)\in S^*$,满足

${\rm Re}\left\{\frac{zf'(z)}{f(z)}\left(\frac{f(z)}{g(z)}\right)^\alpha\right\}>\beta, $

即${\rm Re}q(z)>\beta$.从而

$q(z)\prec\frac{1+(1-2\beta)z}{1-z}.$

记$p(z)=\frac{1+(1-2\beta)z}{1-z}, $由引理2.1可知

$\begin{eqnarray*}\int_0^{2\pi}\left|\frac{q'(z)}{q(z)}\right|{\rm d}\theta&\leq&\int_0^{2\pi}\left|\frac{p'(z)}{p(z)}\right|{\rm d}\theta =(2-2\beta)\int_0^{2\pi}\left|\frac{1}{(1-z)[1+(1-2\beta)z]}\right|{\rm d}\theta\\ &=&\frac{2-2\beta}{r}\int_0^{2\pi}\left|\frac{z}{(1-z)[1+(1-2\beta)z]}\right|{\rm d}\theta\\ &\leq&\frac{2-2\beta}{r}\int_0^{r}\frac{{\rm d}\rho}{(1-\rho)[1+(1-2\beta)\rho]}\\ &=&\frac{1}{r}\log \frac{1+(1-2\beta)r}{1-r}.\end{eqnarray*}$

所以对$z=r{\rm e}^{{\rm i}\theta}$,有

$\begin{eqnarray*}\left|\left\{\frac{zq'(z)}{q(z)}\right\}_n\right|&=&\left|\frac{1}{2\pi{\rm i}}\oint_{|z|=r}\frac{zq'(z)}{q(z)}z^{-n-1}{\rm d}z\right|=\left|\frac{1}{2\pi}\int_{0}^{2\pi}\frac{zq'(z)}{q(z)}r^{-n}{\rm e}^{-{\rm i}n\theta}{\rm d}\theta\right|\nonumber\\&\leq&\frac{r^{-n+1}}{2\pi}\int_0^{2\pi}\left|\frac{q'(z)}{q(z)}\right|{\rm d}\theta\leq\frac{r^{-n}}{2\pi}\log \frac{1+(1-2\beta)r}{1-r}.\end{eqnarray*}$

令$r=1-\frac{1}{n}$,则

$\left|\left\{\frac{zq'(z)}{q(z)}\right\}_n\right|\leq\frac1{2\pi}(1-\frac{1}{n})^{-n}\log [n+(1-2\beta)(n-1)].$

因为当$n\geq2$时有, $(1-\frac{1}{n})^{-n}\leq4$,所以

$\left|\left\{\frac{zq'(z)}{q(z)}\right\}_n\right|\leq\frac2{\pi}\log [2(1-\beta)n+(2\beta-1)].$

由Schwarz不等式可知

$\begin{eqnarray*}\left|\left\{\frac{zq'(z)}{q(z)}F_1(z)\right\}_n\right|&=&\left|\sum\limits_{m=0}^{n-1}\{F_1(z)\}_m\left\{\frac{zq'(z)}{q(z)}\right\}_{n-m}\right|\leq\sum\limits_{m=0}^{n-1}\left|\{F_1(z)\}_m\right|\left|\left\{\frac{zq'(z)}{q(z)}\right\}_{n-m}\right|\nonumber\\&\leq&\sum\limits_{m=0}^{n-1}\left|\{F_1(z)\}_m\right|\frac2{\pi}\log [2(1-\beta)(n-m)+(2\beta-1)]\\&\leq&\frac2{\pi}\log [2(1-\beta)n+(2\beta-1)]\sum\limits_{m=0}^{n}\left|\{F_1(z)\}_m\right|\\&\leq&\frac2{\pi}\log [2(1-\beta)n+(2\beta-1)]\left(\sum\limits_{m=0}^{n}1^2\sum\limits_{m=0}^{n}\left|\{F_1(z)\}_m\right|^2\right)^{\frac{1}{2}}\\&=&\frac2{\pi}\log [2(1-\beta)n+(2\beta-1)]n^{\frac12}\left(\sum\limits_{m=0}^{n}\left|\{F_1(z)\}_m\right|^2\right)^{\frac{1}{2}}.\end{eqnarray*}$

同理可证

$\left|\left\{\frac{zq'(z)}{q(z)}G_1(z)\right\}_n\right|\leq\frac2{\pi}\log [2(1-\beta)n+(2\beta-1)]n^{\frac12}\left(\sum\limits_{m=0}^{n}\left|\{G_1(z)\}_m\right|^2\right)^{\frac{1}{2}}.$

由引理2.2可知

$\left|\left\{\frac{zq'(z)}{q(z)}F_1(z)\right\}_n\right|\leq\frac2{\pi}{\cal A}^{\frac{1}{2}}_1n^{2\lambda+1}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}}.$

由引理2.3可知

$\left|\left\{\frac{zq'(z)}{q(z)}G_1(z)\right\}_n\right|\leq\frac2{\pi}{\cal B}^{\frac{1}{2}}_1n^{\lambda+1}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}}.$

因为$\frac{z}{1-z}=\sum\limits_{n=1}^\infty z^n$,即$\{\frac{z}{1-z}\}_n=1, n=1, 2, \cdots $,所以由Schwarz不等式可知

$\begin{eqnarray*}\left|\left\{\frac{z}{1-z}G_1(z)\right\}_n\right|&=&\left|\sum\limits_{m=0}^{n-1}\{G_1(z)\}_m\left\{\frac{z}{1-z}\right\}_{n-m}\right|=\left|\sum\limits_{m=0}^{n-1}\{G_1(z)\}_m\right|\\&\leq&\left(\sum\limits_{m=0}^{n}1^2\sum\limits_{m=0}^{n}\left|\{G_1(z)\}_m\right|^2\right)^{\frac{1}{2}}=n^{\frac12}\left(\sum\limits_{m=0}^{n}\left|\{G_1(z)\}_m\right|^2\right)^{\frac{1}{2}}.\end{eqnarray*}$

由引理2.3可知

$\left|\left\{\frac{z}{1-z}G_1(z)\right\}_n\right|\leq{\cal B}_1^{\frac12}n^{\lambda+1}(\log n)^{\frac12}.$

证毕.

引理2.5  设$f(z)\in B_\alpha(\beta)$, $F_1(z)=f(z)^{\lambda-1}f'(z)z^{1-\lambda}$, $G_1(z)=(1-z)f(z)^{\lambda-1}f'(z)z^{1-\lambda}$, $0<\lambda<1$,则

(2.11)$\begin{eqnarray}\left|\left\{\frac{zf''(z)}{f'(z)}F_1(z)\right\}_n\right|&\leq&\frac2{\pi}{\cal A}^{\frac{1}{2}}_1n^{2\lambda+1}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}} \\&&+{\cal A}_2n^{2\lambda+1}(\log n)^{\frac{1}{2}}+(\alpha+|1-\alpha|){\cal A}_3n^{2\lambda+1}\log n, \end{eqnarray}$

(2.12)$\begin{eqnarray}\left|\left\{\frac{zf''(z)}{f'(z)}G_1(z)\right\}_n\right|&\leq&\frac2{\pi}{\cal B}^{\frac{1}{2}}_1n^{\lambda+1}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}} \\&&+{\cal B}_2n^{\lambda+1}(\log n)^{\frac{1}{2}}+(\alpha+|1-\alpha|){\cal B}_3n^{\lambda+1}\log n.\end{eqnarray}$

证  设$f(z)\in B_\alpha(\beta)$,则存在$g(z)\in S^*$使得

${\rm Re}\left\{\frac{zf'(z)}{f(z)}\left(\frac{f(z)}{g(z)}\right)^\alpha\right\}>\beta, $

即

$\frac{\frac{zf'(z)}{f(z)}\left(\frac{f(z)}{g(z)}\right)^\alpha-\beta}{1-\beta}\in P.$

令$q(z)=\frac{zf'(z)}{f(z)}\left(\frac{f(z)}{g(z)}\right)^\alpha$,经简单计算可知

$\frac{zq'(z)}{q(z)}=1+\frac{zf''(z)}{f'(z)}-\alpha\frac{zg'(z)}{g(z)}+(\alpha-1)\frac{zf'(z)}{f(z)}, $

从而有

$\begin{eqnarray*}\left\{\frac{zf''(z)}{f'(z)}F_1(z)\right\}_n&=&\left\{\frac{zq'(z)}{q(z)}F_1(z)\right\}_n-\left\{F_1(z)\right\}_n+\alpha\left\{\frac{zg'(z)}{g(z)}F_1(z)\right\}_n\\&&+(1-\alpha)\left\{\frac{zf'(z)}{f(z)}F_1(z)\right\}_n.\end{eqnarray*}$

所以

$\begin{eqnarray*}\left|\left\{\frac{zf''(z)}{f'(z)}F_1(z)\right\}_n\right|&\leq&\left|\left\{\frac{zq'(z)}{q(z)}F_1(z)\right\}_n\right|+\left|\left\{F_1(z)\right\}_n\right|+\alpha\left|\left\{\frac{zg'(z)}{g(z)}F_1(z)\right\}_n\right|\\&&+|1-\alpha|\left|\left\{\frac{zf'(z)}{f(z)}F_1(z)\right\}_n\right|.\end{eqnarray*}$

同理

$\begin{eqnarray*}\left|\left\{\frac{zf''(z)}{f'(z)}G_1(z)\right\}_n\right|&\leq&\left|\left\{\frac{zq'(z)}{q(z)}G_1(z)\right\}_n\right|+\left|\left\{G_1(z)\right\}_n\right|+\alpha\left|\left\{\frac{zg'(z)}{g(z)}G_1(z)\right\}_n\right|\\&&+|1-\alpha|\left|\left\{\frac{zf'(z)}{f(z)}G_1(z)\right\}_n\right|.\end{eqnarray*} $

由引理2.2和引理2.4可知

$\begin{eqnarray*}\left|\left\{\frac{zf''(z)}{f'(z)}F_1(z)\right\}_n\right|&\leq &\frac2{\pi}{\cal A}^{\frac{1}{2}}_1n^{2\lambda+1}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}}+{\cal A}_2n^{2\lambda+1}(\log n)^{\frac{1}{2}}\\&&+(\alpha+|1-\alpha|){\cal A}_3n^{2\lambda+1}\log n.\end{eqnarray*}$

由引理2.3和引理2.4可知

$\begin{eqnarray*}\left|\left\{\frac{zf''(z)}{f'(z)}G_1(z)\right\}_n\right|&\leq&\frac2{\pi}{\cal B}^{\frac{1}{2}}_1n^{\lambda+1}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}}+{\cal B}_2n^{\lambda+1}(\log n)^{\frac{1}{2}}\\&&+(\alpha+|1-\alpha|){\cal B}_3n^{\lambda+1}\log n.\end{eqnarray*}$

证毕.

引理2.6^[14]  设$f(z)\in S$,则对$z=r{\rm e}^{{\rm i}\theta}$, $0<r<1$,

$|f(z)|\leq\frac{r}{(1-r)^2}.$

引理2.7^[7]  设$f(z)\in S$, $\psi(z)$由(1.1)式定义,则

$\{z\psi(z)\}_n\leq {\cal A}_4n^{\lambda} \log n, \ \ \ 0<\lambda<1.$

引理2.8^[7]  设$f(z)\in S$, $G_2(z)=(1-z)f(z)^\lambda z^{-\lambda}=\sum\limits_{n=1}^\infty\{G_2\}_nz^n, $则

$|\{G_2(z)\}_n|\leq{\cal B}_4n^\lambda.$

证  由文献[7]的证明过程可知.

定理3.1  设$f(z)\in B_\alpha(\beta)$, $D_n(\lambda)$由(1.1)式式定义,则对$n\geq2$有

$\begin{eqnarray*}|D_n|&\leq E_1 n^{2\lambda-1}\log n+E_2n^{2\lambda-1}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}}, \end{eqnarray*}$

其中$E_1, E_2$是绝对常数,阶$2\lambda-1$是最佳的.

证  由(1.1)式,可算出

(3.1)$\begin{equation}z\psi'(z)=\lambda F_1(z)-\lambda F_2(z), \end{equation}$

其中

(3.2)$\begin{equation}F_1(z)=f(z)^{\lambda-1}f'(z)z^{1-\lambda}=\sum\limits_{n=1}^\infty\{F_1\}_nz^n, \end{equation}$

(3.3)$\begin{equation}F_2(z)=f(z)^\lambda z^{-\lambda}=\sum\limits_{n=1}^\infty\{F_2\}_nz^n.\end{equation}$

因为

$zF_1'(z)=(\lambda-1)\frac{zf'(z)}{f(z)}F_1(z)+(1-\lambda)F_1(z)+\frac{zf''(z)}{f'(z)}F_1(z), $

所以

$\left\{zF_1'(z)\right\}_n=(\lambda-1)\left\{\frac{zf'(z)}{f(z)}F_1(z)\right\}_n+(1-\lambda)\{F_1(z)\}_n+\left\{\frac{zf''(z)}{f'(z)}F_1(z)\right\}_n, $

从而

$|\{zF_1'(z)\}_n|\leq(1-\lambda)\left|\left\{\frac{zf'(z)}{f(z)}F_1(z)\right\}_n\right|+(1-\lambda)|\{F_1(z)\}_n|+\left|\left\{\frac{zf''(z)}{f'(z)}F_1(z)\right\}_n\right|.$

由引理2.2和引理2.5可知

$\begin{eqnarray*}|\{zF_1'(z)\}_n|&\leq &(1-\lambda){\cal A}_3n^{2\lambda+1}\log n+(1-\lambda){\cal A}_2n^{2\lambda+1}(\log n)^{\frac{1}{2}}\\&&+\frac2{\pi}{\cal A}^{\frac{1}{2}}_1n^{2\lambda+1}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}}+{\cal A}_2n^{2\lambda+1}(\log n)^{\frac{1}{2}}\\&&+(\alpha+|1-\alpha|){\cal A}_3n^{2\lambda+1}\log n.\end{eqnarray*}$

由(3.2)式可知

$zF_1'(z)=\sum\limits_{n=1}^\infty n\{F_1\}_nz^n, $

所以

$\begin{eqnarray*}|n\{F_1\}_n|=|\{zF_1'(z)\}_n|&\leq& (1-\lambda){\cal A}_3n^{2\lambda+1}\log n+(1-\lambda){\cal A}_2n^{2\lambda+1}(\log n)^{\frac{1}{2}}\\&&+\frac2{\pi}{\cal A}^{\frac{1}{2}}_1n^{2\lambda+1}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}}\\&&+{\cal A}_2n^{2\lambda+1}(\log n)^{\frac{1}{2}}+(\alpha+|1-\alpha|){\cal A}_3n^{2\lambda+1}\log n.\end{eqnarray*}$

即

(3.4)$\begin{eqnarray}|\{F_1\}_n|&\leq &(1-\lambda){\cal A}_3n^{2\lambda}\log n+(1-\lambda){\cal A}_2n^{2\lambda}(\log n)^{\frac{1}{2}} \\&&+\frac2{\pi}{\cal A}^{\frac{1}{2}}_1n^{2\lambda}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}}+{\cal A}_2n^{2\lambda}(\log n)^{\frac{1}{2}} \\&&+(\alpha+|1-\alpha|){\cal A}_3n^{2\lambda}\log n.\end{eqnarray}$

由(3.3)式可知

$\begin{eqnarray*}|\{F_2\}_n|&=&\left|\frac{1}{2\pi {\rm i}}\oint_{|z|=r}\frac{f(z)^\lambda z^{-\lambda}}{z^{n+1}}{\rm d}z\right|=\left|\frac{1}{2\pi}\int_{0}^{2\pi}\frac{f(z)^\lambda }{r^{n+\lambda}}{\rm e}^{-{\rm i}(n+\lambda)\theta}{\rm d}\theta\right|\\&\leq&\frac{1}{2\pi r^{n+\lambda}}\int_{0}^{2\pi}|f(z)|^\lambda {\rm d}\theta.\end{eqnarray*}$

由引理2.6可知

$|\{F_2\}_n|\leq\frac{1}{r^n}\frac{1}{(1-r)^{2\lambda}}.$

令$r=1-\frac{1}{n}$,则当$n\geq2$时,有

(3.5)$\begin{equation}|\{F_2\}_n|\leq(1-\frac{1}{n})^{-n}n^{2\lambda}\leq4n^{2\lambda}.\end{equation}$

由(3.1)式可知

$nD_n=\lambda \{F_1(z)\}_n-\lambda \{F_2(z)\}_n.$

从而由(3.4)式和(3.5)式可知

$\begin{eqnarray*}n|D_n|&\leq&\lambda |\{F_1(z)\}_n|+\lambda |\{F_2(z)\}_n|\leq\lambda(1-\lambda){\cal A}_3n^{2\lambda}\log n+\lambda(1-\lambda){\cal A}_2n^{2\lambda}(\log n)^{\frac{1}{2}}\\&&+\frac{2\lambda}{\pi}{\cal A}^{\frac{1}{2}}_1n^{2\lambda}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}}+\lambda{\cal A}_2n^{2\lambda}(\log n)^{\frac{1}{2}}\\&&+\lambda(\alpha+|1-\alpha|){\cal A}_3n^{2\lambda}\log n+4\lambda n^{2\lambda}.\end{eqnarray*}$

即

$|D_n|\leq E_1 n^{2\lambda-1}\log n+E_2n^{2\lambda-1}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}}.$

其中$E_1=4\lambda(\log 2)^{-1}+\lambda(2-\lambda){\cal A}_2(\log 2)^{-\frac12}+[\lambda(1-\lambda)+\lambda(\alpha+|1-\alpha|)]{\cal A}_3$, $E_2=\frac{2\lambda}{\pi}{\cal A}^{\frac{1}{2}}_1$是绝对常数.

取$f(z)=\frac{z}{(1-z)^2}$,则

$\begin{eqnarray*}\psi(z)=\left[\frac{f(z)}{z}\right]^\lambda=\left[\frac{1}{(1-z)^2}\right]^\lambda=1+\sum\limits_{n=1}^{\infty}D_n(\lambda)z^n, \end{eqnarray*}$

其中

$ D_n(\lambda)=\frac{(2\lambda+n-1)(2\lambda+n-2)\cdots (2\lambda+1)2\lambda}{n!}, $

而

$\begin{eqnarray*}D_n(\lambda)&=&\frac{(2\lambda+n-1)(2\lambda+n-2)\cdots (2\lambda+1)2\lambda}{n!}\\&=&\left(\frac{2\lambda}{n-1}+1\right)\left(\frac{2\lambda}{n-2}+1\right)\cdots \left(\frac{2\lambda}{1}+1\right)\frac{2\lambda}{n}\\&\leq& \frac{2\lambda}{n}e^{\frac{2\lambda}{n-1}}e^{\frac{2\lambda}{n-2}}\cdots e^{\frac{2\lambda}{1}}=\frac{2\lambda}{n}e^{2\lambda(1+1/2+1/3+\cdots+1/(n-1))}.\end{eqnarray*}$

由于

$1+\frac12+\frac13+\cdots+\frac{1}{n-1}\leq\gamma+\log n, $

其中, $\gamma\approx0.5772156649$为欧拉常数.故

$\begin{eqnarray*}D_n(\lambda)&\leq&\frac{2\lambda}{n}e^{2\lambda(1+1/2+1/3+\cdots+1/(n-1))}\\&\leq&\frac{2\lambda}{n}e^{2\lambda(\gamma+\log n)}=2\lambda e^{2\lambda\gamma}n^{2\lambda-1}.\end{eqnarray*}$

其中$2\lambda e^{2\lambda\gamma}$是常数,所以阶$2\lambda-1$是最佳的.

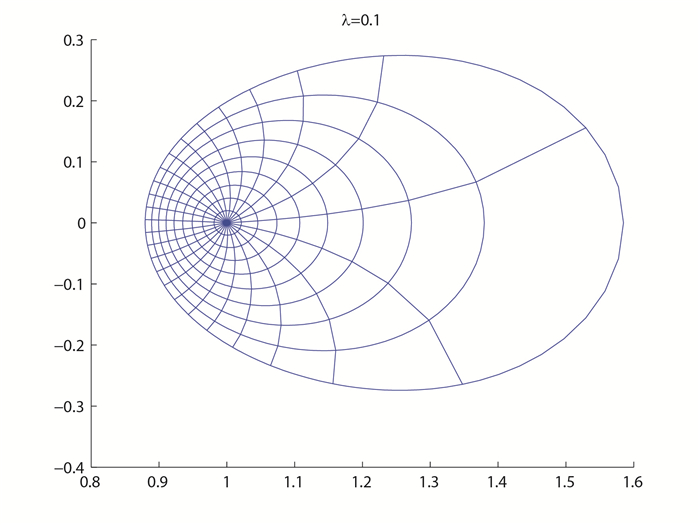
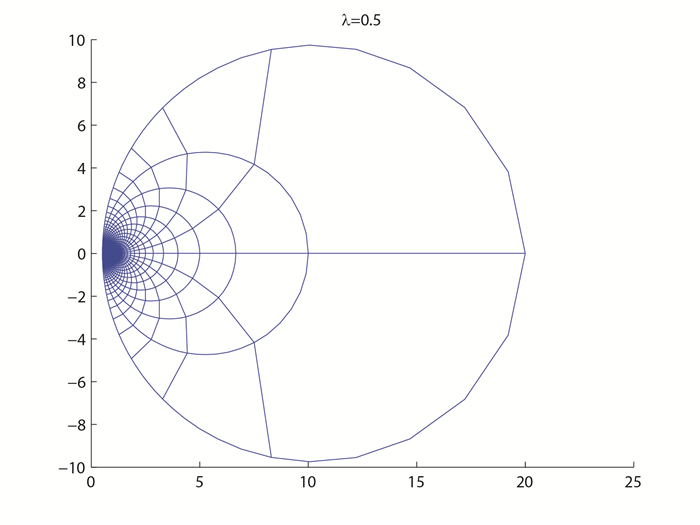
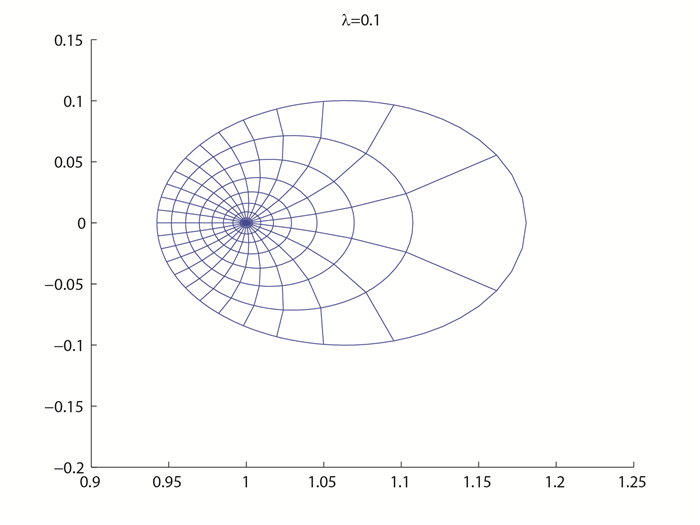
特别地,我们分别画出了当$\lambda=0.1, \lambda=0.5, \lambda=0.9$, $f(z)=\frac{z}{(1-z)^2}$时, Milin函数$\psi(z)$的图像,见图 1, 图 2, 图 3.

在定理3.1中令$\beta=0$,可得文献[3,定理1].

推论3.1  设$f(z)\in B_\alpha$, $D_n(\lambda)$由(1.1)式定义,则对$n\geq2$有

$|D_n|\leq En^{2\lambda-1}(\log n)^{\frac{3}{2}}, $

其中$E$是绝对常数.

证  令$\beta=0$,由定理3.1可知

$\begin{eqnarray*}|D_n|&\leq E_1 n^{2\lambda-1}\log n+E_2n^{2\lambda-1}\log (2n-1) (\log n)^{\frac{1}{2}}.\end{eqnarray*}$

因为当$n\geq2$时, $\log (2n-1)\leq2\log n$,所以

$\begin{eqnarray*}|D_n|&\leq& E_1 (\log 2)^{-\frac{1}{2}}n^{2\lambda-1}(\log n)^{\frac{3}{2}}+2E_2n^{2\lambda-1}(\log n)^{\frac{3}{2}}\\&=&En^{2\lambda-1}(\log n)^{\frac{3}{2}}.\end{eqnarray*}$

其中$E=E_1 (\log 2)^{-\frac{1}{2}}+2E_2$是绝对常数.

定理3.2  设$f(z)\in B_\alpha(\beta)$, $D_n(\lambda)$由(1.1)式定义,则对$n\geq2$有

$\begin{eqnarray*}||D_{n+1}|-|D_n||&\leq& C_1(n+1)^{\lambda-1}\log (n+1)\\&&+C_2(n+1)^{\lambda-1}\log [2(1-\beta)(n+1)+(2\beta-1)](\log (n+1))^{\frac{1}{2}}, \end{eqnarray*}$

其中$C_1, C_2$是绝对常数,阶$\lambda-1$是最佳的.

证  因为$\psi(z)=\left[\frac{f(z)}{z}\right]^\lambda=1+\sum\limits_{n=1}^\infty D_n(\lambda)z^n, f(z)\in S, 0<\lambda<1, $经简单计算可知

(3.6)$\begin{equation}z[\psi(z)-z\psi(z)]'=\sum\limits_{n=1}^\infty(n+1)(D_{n+1}-D_n)z^{n+1}+(D_1-1)z.\end{equation}$

即

$\begin{eqnarray*}(n+1)(D_{n+1}-D_n)&=&\{z[\psi(z)-z\psi(z)]'\}_{n+1}\\&=&\{(z-z^2)\psi'(z)\}_{n+1}+\{-z\psi(z)\}_{n+1}.\end{eqnarray*}$

所以

$||D_{n+1}|-|D_n||\leq|D_{n+1}-D_n|\leq\frac{1}{n+1}[|\{(z-z^2)\psi'(z)\}_{n+1}|+|\{-z\psi(z)\}_{n+1}|].$

由引理2.7可知

$\{z\psi(z)\}_{n+1}\leq {\cal A}_4(n+1)^{\lambda} \log (n+1).$

下面计算$|\{(z-z^2)\psi'(z)\}_{n+1}|$的界.

由(1.1)式,可算出

(3.7)$\begin{equation}(z-z^2)\psi'(z)=\lambda G_1(z)-\lambda G_2(z).\end{equation}$

其中

(3.8)$\begin{equation}G_1(z)=(1-z)f(z)^{\lambda-1}f'(z)z^{1-\lambda}=\sum\limits_{n=1}^\infty\{G_1\}_nz^n, \end{equation}$

(3.9)$\begin{equation}G_2(z)=(1-z)f(z)^\lambda z^{-\lambda}=\sum\limits_{n=1}^\infty\{G_2\}_nz^n.\end{equation}$

因为

$zG_1'(z)=(\lambda-1)\frac{zf'(z)}{f(z)}G_1(z)+(1-\lambda)G_1(z)+\frac{zf''(z)}{f'(z)}G_1(z)-\frac{z}{1-z}G_1(z).$

所以

$\begin{eqnarray*}\left\{zG_1'(z)\right\}_n&=&(\lambda-1)\left\{\frac{zf'(z)}{f(z)}G_1(z)\right\}_n+(1-\lambda)\{G_1(z)\}_n+\left\{\frac{zf''(z)}{f'(z)}G_1(z)\right\}_n\\&&+\bigg\{-\frac{z}{1-z}G_1(z)\bigg\}_n.\end{eqnarray*}$

从而

$\begin{eqnarray*}|\{zG_1'(z)\}_n|&\leq&(1-\lambda)\left|\left\{\frac{zf'(z)}{f(z)}G_1(z)\right\}_n\right|+(1-\lambda)|\{G_1(z)\}_n|+\left|\left\{\frac{zf''(z)}{f'(z)}G_1(z)\right\}_n\right|\\&&+\left|\bigg\{\frac{z}{1-z}G_1(z)\bigg\}_n\right|.\end{eqnarray*}$

由引理2.3引理2.4和引理2.5可知

$\begin{eqnarray*}|\{zG_1'(z)\}_n|&\leq& (1-\lambda){\cal B}_3n^{\lambda+1}\log n+(1-\lambda){\cal B}_2n^{\lambda+1}(\log n)^{\frac{1}{2}}\\&&+\frac2{\pi}{\cal B}^{\frac{1}{2}}_1n^{\lambda+1}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}}+{\cal B}_2n^{\lambda+1}(\log n)^{\frac{1}{2}}\\&&+(\alpha+|1-\alpha|){\cal B}_3n^{\lambda+1}\log n+{\cal B}_1^{\frac12}n^{\lambda+1}(\log n)^{\frac12}.\end{eqnarray*}$

由(3.8)式可知

$zG_1'(z)=\sum\limits_{n=1}^\infty n\{G_1\}_nz^n, $

所以

$\begin{eqnarray*}|n\{G_1\}_n|=|\{zG_1'(z)\}_n|&\leq & (1-\lambda){\cal B}_3n^{\lambda+1}\log n+(1-\lambda){\cal B}_2n^{\lambda+1}(\log n)^{\frac{1}{2}}\\&&+\frac2{\pi}{\cal B}^{\frac{1}{2}}_1n^{\lambda+1}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}}+{\cal B}_2n^{\lambda+1}(\log n)^{\frac{1}{2}}\\&&+(\alpha+|1-\alpha|){\cal B}_3n^{\lambda+1}\log n+{\cal B}_1^{\frac12}n^{\lambda+1}(\log n)^{\frac12}.\end{eqnarray*}$

即

(3.10)$\begin{eqnarray}|\{G_1\}_n|&\leq&(1-\lambda){\cal B}_3n^{\lambda}\log n+(1-\lambda){\cal B}_2n^{\lambda}(\log n)^{\frac{1}{2}} \\&&+\frac2{\pi}{\cal B}^{\frac{1}{2}}_1n^{\lambda}\log [2(1-\beta)n+(2\beta-1)] (\log n)^{\frac{1}{2}}+{\cal B}_2n^{\lambda}(\log n)^{\frac{1}{2}} \\&&+(\alpha+|1-\alpha|){\cal B}_3n^{\lambda}\log n+{\cal B}_1^{\frac12}n^{\lambda}(\log n)^{\frac12}.\end{eqnarray}$

由引理2.8可知

(3.11)$\begin{equation}|\{G_2\}_n|\leq{\cal B}_4n^\lambda.\end{equation}$

由(3.10)和(3.11)式可知

$\begin{eqnarray*}|\{(z-z^2)\psi'(z)\}_{n+1}|&\leq&\lambda|\{G_1\}_{n+1}|+\lambda|\{G_2\}_{n+1}|\\&\leq& \lambda(1-\lambda){\cal B}_3(n+1)^{\lambda}\log (n+1)+\lambda(1-\lambda){\cal B}_2(n+1)^{\lambda}(\log (n+1))^{\frac{1}{2}}\\&&+\frac2{\pi}\lambda{\cal B}^{\frac{1}{2}}_1(n+1)^{\lambda}\log [2(1-\beta)(n+1)+(2\beta-1)] (\log (n+1))^{\frac{1}{2}}\\&&+{\cal B}_2\lambda (n+1)^{\lambda}(\log (n+1))^{\frac{1}{2}}+\lambda(\alpha+|1-\alpha|){\cal B}_3(n+1)^{\lambda}\log (n+1)\\&&+{\cal B}_1^{\frac12}\lambda (n+1)^{\lambda}(\log (n+1))^{\frac12}+{\cal B}_4\lambda (n+1)^\lambda.\end{eqnarray*}$

综上可知

$\begin{eqnarray*}||D_{n+1}|-|D_n||&\leq&|D_{n+1}-D_n|\\&\leq&\frac{1}{n+1}[|\{(z-z^2)\psi'(z)\}_{n+1}|+|\{-z\psi(z)\}_{n+1}|]\\&\leq& C_1(n+1)^{\lambda-1}\log (n+1)\\&&+C_2(n+1)^{\lambda-1}\log [2(1-\beta)(n+1)+(2\beta-1)](\log (n+1))^{\frac{1}{2}}.\end{eqnarray*}$

其中$C_1={\cal B}_4\lambda(\log 3)^{-1}+{\cal B}_2\lambda(2-\lambda)(\log 3)^{-\frac12}+{\cal B}_1^{\frac12}\lambda(\log 3)^{-\frac12}+\lambda(1-\lambda){\cal B}_3+\lambda(\alpha+|1-\alpha|){\cal B}_3+{\cal A}_4$, $C_2=\frac2{\pi}\lambda{\cal B}^{\frac{1}{2}}_1$是绝对常数.

取$f(z)=\frac{z}{1-z^2}$,则

$\begin{eqnarray*}\psi(z)=\left[\frac{f(z)}{z}\right]^\lambda=\left[\frac{1}{1-z^2}\right]^\lambda=1+\sum\limits_{n=1}^{\infty}D_n(\lambda)z^n, \end{eqnarray*}$

其中

$ D_{2n-1}(\lambda)=0, \ \ \ D_{2n}(\lambda)=\frac{\lambda(\lambda+1)(\lambda+2)\cdots (\lambda+n-1)}{n!}, \ \ \ n=1, 2, \cdots.$

而

$\begin{eqnarray*}D_{2n}(\lambda)&=&\frac{\lambda(\lambda+1)(\lambda+2)\cdots (\lambda+n-1)}{n!}\\&=&\frac{\lambda}{n} \left(1+\frac{\lambda}{1}\right) \left(1+\frac{\lambda}{2}\right)\cdots\left(1+\frac{\lambda}{n-2}\right)\left(1+\frac{\lambda}{n-1}\right)\\&\leq& \frac{\lambda}{n}e^{\frac{\lambda}{1}}e^{\frac{\lambda}{2}}\cdots e^{\frac{\lambda}{n-2}}e^{\frac{\lambda}{n-1}}\\&=&\frac{\lambda}{n}e^{\lambda(1+1/2+1/3+\cdots+1/(n-1))}, \end{eqnarray*}$

由于

$1+\frac12+\frac13+\cdots+\frac{1}{n-1}\leq\gamma+\log n, $

其中$\gamma\approx0.5772156649$为欧拉常数.故

$\begin{eqnarray*}||D_{2n}(\lambda)|-|D_{2n-1}(\lambda)||=|D_{2n}(\lambda)|&\leq&\frac{\lambda}{n}e^{\lambda(1+1/2+1/3+\cdots+1/(n-1))}\\&\leq&\frac{\lambda}{n}e^{\lambda(\gamma+\log n)}=\lambda e^{\lambda\gamma}n^{\lambda-1}\end{eqnarray*}$

其中$\lambda e^{\lambda\gamma}$是常数,所以阶$\lambda-1$是最佳的.

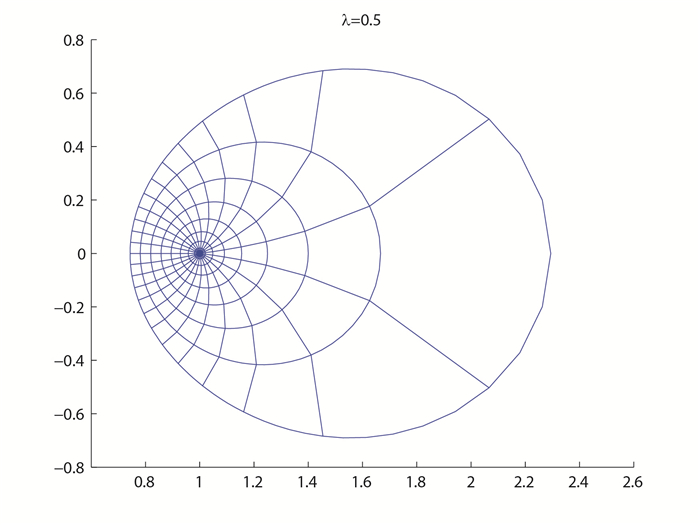
特别地,我们分别画出了当$\lambda=0.1, \lambda=0.5, \lambda=0.9$, $f(z)=\frac{z}{1-z^2}$时, $\left[\frac{f(z)}{z}\right]^\lambda$的图像,见图 4, 图 5, 图 6.

在定理3.2中令$\beta=0$,可得文献[7]的定理.

推论3.2  设$f(z)\in B_\alpha$, $D_n(\lambda)$由(1.1)式定义,则对$n\geq2$有

$||D_{n+1}|-|D_n||\leq A(n+1)^{\lambda-1}(\log (n+1))^{\frac{3}{2}}.$

其中$A$是绝对常数.

证  令$\beta=0$,由定理3.2可知

$||D_{n+1}|-|D_n||\leq C_1(n+1)^{\lambda-1}\log (n+1)+C_2(n+1)^{\lambda-1}\log (2n+1)(\log (n+1))^{\frac{1}{2}}.$

因为当$n\geq2$时, $\log 2(n+1)\leq2\log (n+1)$,所以

$\begin{eqnarray*}||D_{n+1}|-|D_n||&\leq &C_1(\log 3)^{-\frac12}(n+1)^{\lambda-1}(\log (n+1))^{\frac{3}{2}}+2C_4(n+1)^{\lambda-1}(\log (n+1))^{\frac{3}{2}}\\&=&A(n+1)^{\lambda-1}(\log (n+1))^{\frac{3}{2}}, \end{eqnarray*}$

其中$A=C_1(\log 3)^{-\frac12}+2C_4$是绝对常数.