1 引言
设
的函数类.
1967年, Macgregor[1]给出了优化的定义.
定义1.1 设函数
则称函数
1970年, Roberston[2]引入了拟从属的概念.
定义1.2 设函数
满足
则称函数
1981年, Salagean[4]引入算子
若
利用上述Salagean算子和从属关系,我们定义解析函数的两个新子类
定义1.3 设函数
这里
注1.1 在定义1.3中,若参数
(1)若取
(2)若取
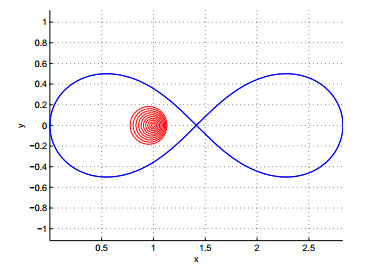
蕴含
图 1
(3)若取
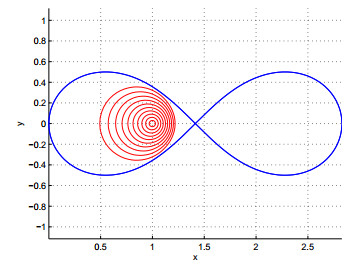
蕴含
图 2
定义1.4 设函数
这里
注1.2 在定义1.4中,若参数
(1)若取
(2)若取
蕴含
(3)若取
蕴含
(4)若取
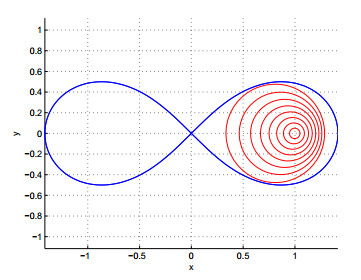
蕴含
图 3
(5)若取
蕴含
图 4
1967年, MacGregor[1]最早开始研究星象函数类的优化问题.随后, 2001年, Altintas等人[8, 9]研究了复阶单(多)叶星象和凸像函数类的优化问题.近年来,许多中外学者对由各种算子定义的不同单(多)叶解析函数类的优化问题作了大量研究,如Goyal等人[10, 11], Goswami等人[12], Prajapat等人[13],汤获等人[14-16].最近,汤获等人[17]又讨论了多叶亚纯解析函数类的优化问题.然而,我们发现,很少有人研究伯努利双纽线区域内解析函数类的优化问题.在上述工作的基础上,本文主要研究伯努利双纽线左、右半有界区域内复阶解析函数类
2 函数类Lγn Rbn(a,c)
首先,我们给出并证明函数类
定理2.1 设
其中
证 由于
其中
的解析函数类[18].
根据(2.2)式和(2.3)式,可得
又
对上式两边关于
又注意到
故将(2.4)式和(2.6)式代入(2.5)式,有
若取
其中
要确定
其中
显然,当
这里
又
下面,我们讨论函数类
定理2.2 设函数
其中
证 因为
这里
利用(2.3)式和(2.8)式,易有
再将(2.6)式和(2.9)式代入(2.5)式,类似于定理2.1的证明,易得
令
其中
当
即有
定理2.2得证.
3 一些推论
在定理2.1中,若分别取
推论3.1 设函数
其中
推论3.2 设函数
其中
推论3.3 设函数
其中
在定理2.2中,若取
推论3.4 设函数
其中
在推论3.4中,若分别取
推论3.5 设函数
其中
推论3.6 设函数
其中
进一步,在推论3.5和推论3.6中,若分别取
推论3.7 设函数
其中
推论3.8 设函数
其中
参考文献
Majorization by univalent functions
DOI:10.1215/S0012-7094-67-03411-4 [本文引用: 2]
Quasi-subordination and coefficient conjectures
DOI:10.1090/S0002-9904-1970-12356-4 [本文引用: 1]
A subclass of starlike functions associated with left-half of the lemniscate of Bernoulli
Radius of convexity of some subclasses of strongly starlike functions
Some majorization problems associated with p-valently starlike and convex functions of complex order
Majorization by starlike functions of complex order
Majorization for certain classes of analytic functions defined by fractional derivatives
DOI:10.1016/j.aml.2009.07.009 [本文引用: 1]
Majorization for certain classes of meromorphic functions defined by integral operator
Majorization properties for certain classes of analytic functions using the Salagean operator
DOI:10.1016/j.aml.2010.06.030 [本文引用: 1]
Majorization problem for certain class of p-valently analytic functions defined by generalized fractional differintegral operator
DOI:10.1016/j.camwa.2011.10.065 [本文引用: 1]
Majorization properties for certain classes of analytic functions involving a generalized differential operator
Majorization properties for a new subclass of θ-spiral functions of order γ
Majorization properties for certain new classes of analytic functions using the Salagean operator
DOI:10.1186/1029-242X-2013-86 [本文引用: 1]
Majorization problems for certain subclasses of meromorphic multivalent functions associated with the Liu-Srivastava operator
DOI:10.2298/FIL1504763T [本文引用: 1]