非线性偏微分方程广泛用于研究各种复杂的非线性问题,如核物理、非线性光学、等离子体物理、天体物理、生物物理和其他应用科学.随着符号计算的发展^[1-19],许多求解非线性问题的有效方法被提出,比如逆散射方法^[20], Bäcklund变换方法^[21], Hirota双线性方法^[22],双曲函数方法^[23],齐次平衡法^[24], $F$ -展开式法^[25],指数函数法^[26],相似变换法^[27],辅助方程法^[28],三波测试法^[29-30]等等.

在本文中,我们将研究所谓的(3+1)维Potential-Yu-Toda-Sasa-Fukuyama (Potential-YTSF)方程

(1.1) $\begin{equation}\label{eq:1.1} u_{xxxz}+4\, u_x\, u_{xz}+2\, u_z\, u_{xx}-4\, u_{xt}+3\, u_{yy}=0.\end{equation}$

它经常用来描述区域内孤子和非线性波的动力学,包括流体力学、等离子体物理、弱色散介质等. Potential-YTSF方程是由以下方程简化而成^[31]

(1.2) $\begin{equation}\label{eq:1.2} [-4\, v_t+\Phi(v)\, v_z]_x+3\, v_{yy}=0, \Phi=\partial^2+4v+2v_x\, \partial^{-1}, \end{equation}$

是Yu, Toda, Sasa和Fukuyama等人在研究下列(2+1)维Calogero-Bogoyavlenkii-Schiff方程时提出的一个新方程^[32]

(1.3) $\begin{equation}\label{eq:1.3} -4\, v_t+\Phi(v)\, v_z=0, \Phi=\partial^2+4v+2v_x\, \partial^{-1}.\end{equation}$

令$v =u_x$,方程(1.2)变为Potential-YTSF方程(1.1)^[33].令$z = x$,方程(1.1)变为potential Kadomtsev-Petviashvili(PKP)方程.当$u_y = 0$,方程(1.1)退化成potential Korteweg-de Vries (KdV)方程. Yan^[34]等人利用变换$v = 2\, (\ln \Phi)x+u $构建了方程(1.1)的Bäcklund变换,获得了许多分离变量解^[34-38].

论文的主要结构如下.在第2节,我们利用三波测试法获得了行波多孤子解,其中包括了许多奇异周期孤子解,周期交叉扭结波解,双孤立波解和双周期孤立波解.并利用一些图形讨论了呼吸子和孤子的交互作用和传播特点.第3节对论文结果进行了总结.

为了求解新的周期孤子解,我们假设$\eta=x+\omega z$,代入(1.1)可得^[39]

(2.1) $\begin{equation}\label{eq:b1} \omega u_{\eta\eta\eta\eta}+6 \omega\, u_\eta\, u_{\eta\eta}-4\, u_{\eta t}+3\, u_{yy}=0.\end{equation}$

假设(2.1)有如下形式的解

(2.2) $\begin{equation}\label{eq:b2} u(\eta, y, t)=2\, [\ln f(\eta, y, t)]_\eta, \end{equation}$

其中$f(\eta, y, t)$是待定函数.为了求解方便我们做如下假设

(2.3) $\begin{equation}\label{eq:b3} f(\eta, y, t) = {\rm e}^{\theta_1} k_1+{\rm e}^{-\theta_1}+k_2 \cos \theta_2 +k_3 \sinh \theta_3 +k_4 \sin \theta_4, \end{equation}$

其中$\theta_i=\alpha _i\, \eta+\beta _i\, y+\delta _i\, t+\sigma _i, i=1, 2, 3, 4$和$\alpha _i$, $\beta _i$, $\delta _i$, $\sigma _i$均是待定常数.将方程(2.2)和(2.3)代入方程(2.1)中,令函数${\rm e}^{\theta _1}$, ${\rm e}^{-\theta _1}$, $\sin \left(\theta _2\right)$, $\cos \left(\theta _2\right)$, $\sinh \left(\theta _3\right)$, $\cosh \left(\theta _3\right)$, $\sinh \left(\theta _4\right)$, $\cosh \left(\theta _4\right)$的系数以及常数项为0,我们得到一系列关于参数$\alpha _i$, $\beta _i$, $\delta _i$, $k_i(i=1, 2, 3, 4)$的方程.利用Mathematica软件求解这些代数方程可得如下结果.

情形1

(2.4) $ \begin{eqnarray} k_3&=&0, k_1=k_4=0, \delta_2=\frac{3 \beta _2^2-4 \omega \alpha _2^4}{4 \alpha _2}, \delta_1=\frac{4 \omega \alpha _2^2 \alpha _1^3-3 \beta _2^2 \alpha _1+6 \alpha _2 \beta _1 \beta _2}{4 \alpha _2^2}, \\ \beta_2&=&\frac{\alpha _1 \alpha _2 \beta _1\pm\sqrt{\omega \alpha _2^2 \alpha _1^6+2 \omega \alpha _2^4 \alpha _1^4+\omega \alpha _2^6 \alpha _1^2}}{\alpha _1^2}, \end{eqnarray}$

其中$\alpha_1$, $\alpha_2$和$\beta_1$是任意常数.将这些参数的值代入方程(2.3),可得

(2.5) $\begin{eqnarray}f= {\rm e}^{-\eta \alpha _1-y \beta _1-t \frac{4 \omega\alpha _2^2 \alpha _1^3-3 \beta _2^2 \alpha _1+6 \alpha _2 \beta _1 \beta _2}{4 \alpha _2^2}-\sigma_1}+ k_2\, \cos \Big[\eta \alpha _2+y \beta _2+t \frac{3\beta _2^2-4 \omega \alpha _2^4}{4 \alpha _2}+\sigma _2\Big].\end{eqnarray}$

因此,我们获得了方程(1.1)第一种形式的周期解

(2.6) ${\begin{eqnarray} u_1&=&\Big[-2 {\rm e}^{-\eta \alpha _1-y \beta_1-\frac{t \left(4 \omega \alpha _2^2 \alpha _1^3-3 \beta _2^2 \alpha _1+6 \alpha _2 \beta _1 \beta _2\right)}{4 \alpha _2^2}-\sigma _1} \alpha _1-2 k_2 \alpha _2 \sin \Big [\eta \alpha _2+y \beta _2+\sigma _2\\ &&+\frac{t \left(3 \beta _2^2-4 \omega \alpha _2^4\right)}{4 \alpha _2}\Big]\Big ] \Big/\Big [k_2 \cos\Big [\eta \alpha _2+y \beta _2+\sigma _2+\frac{t \left(3 \beta _2^2-4 \omega \alpha _2^4\right)}{4 \alpha _2}\Big]\\ &&+{\rm e}^{-\eta \alpha _1-y \beta _1-\frac{t \left(4 \omega \alpha _2^2 \alpha _1^3-3 \beta _2^2 \alpha _1+6 \alpha _2 \beta _1 \beta _2\right)}{4 \alpha _2^2}-\sigma _1}\Big], \end{eqnarray}}$

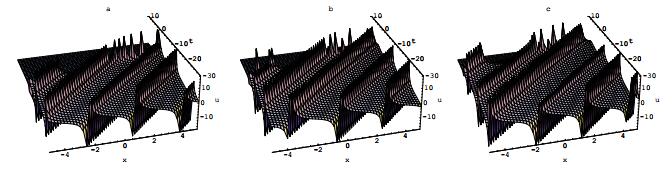
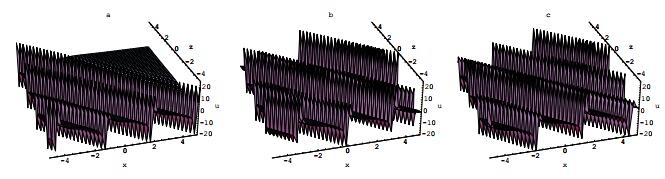
其中所有的参数在方程(2.4)中已列出.方程(2.6)的物理性质和特点被展示在图 1.

情形2

(2.7) $ {\begin{eqnarray}k_3&=&k_4=0, \delta_2=-\frac{{\rm i}\left(3 \beta _2^2-4 \omega \alpha _1^4\right)}{4 \alpha _1 \epsilon _1}, \delta_1=\frac{4 \omega \alpha _1^4+3 \beta _1^2}{4 \alpha _1}, \\ \beta_1& =& -{\rm i} \beta _2 \epsilon _1, \alpha _2={\rm i} \alpha _1 \epsilon _1, \end{eqnarray}}$

其中$\alpha_1$和$\beta_2$是任意常数, $\epsilon _1=\pm1$.将这些参数的值代入方程(2.3),可得

(2.8) ${\begin{eqnarray} f(\eta, y, t)&=& k_1 {\rm e}^{\eta \alpha _1+\sigma _1-\frac{{\rm i}y \beta _2}{\epsilon _1}+\frac{t \left(4 \omega \alpha _1^4-3 \beta _2^2\right)}{4 \alpha _1}}+{\rm e}^{-\eta \alpha _1-\sigma _1+\frac{{\rm i}y \beta _2}{\epsilon _1}-\frac{t \left(4 \omega \alpha _1^4-3 \beta _2^2\right)}{4 \alpha _1}}\\ & &+ k_2 \cos \Big [y \beta _2+{\rm i}\eta \alpha _1 \epsilon _1+\sigma _2-\frac{{\rm i}t \left(3 \beta _2^2-4 \omega \alpha _1^4\right)}{4 \alpha _1 \epsilon _1}\Big].\end{eqnarray}}$

因此,我们获得了方程(1.1)第二种形式的周期解

(2.9) ${\begin{eqnarray} u_2&=&\Big[ 2 k_1 \alpha _1 {\rm e}^{\eta \alpha _1+\sigma _1-\frac{{\rm i}y \beta _2}{\epsilon _1}+\frac{t \left(4 \omega \alpha _1^4-3 \beta _2^2\right)}{4 \alpha _1}} -2 {\rm i}k_2 \epsilon _1 \alpha _1 \sin \Big [y \beta _2+{\rm i} \eta \alpha _1 \epsilon _1+\sigma _2\\ &&-\frac{{\rm i}t \left(3 \beta _2^2-4 \omega \alpha _1^4\right)}{4 \alpha _1 \epsilon _1}\Big] - 2 \alpha _1 {\rm e}^{-\eta \alpha _1-\sigma _1+\frac{{\rm i}y \beta _2}{\epsilon _1}-\frac{t \left(4 \omega \alpha _1^4-3 \beta _2^2\right)}{4 \alpha _1}}\Big] \Big/\Big[k_2 \cos [y \beta _2\\ & &+ {\rm i}\eta \alpha _1 \epsilon _1+\sigma _2-\frac{{\rm i}t \left(3 \beta _2^2-4 \omega \alpha _1^4\right)} {4 \alpha _1 \epsilon _1}\Big]+k_1 {\rm e}^{\eta \alpha _1+\sigma _1-\frac{{\rm i}y \beta_2}{\epsilon _1}+\frac{t \left(4 \omega \alpha _1^4-3 \beta _2^2\right)}{4 \alpha _1}}\\ & &+{\rm e}^{-\eta \alpha _1-\sigma _1+\frac{{\rm i}y \beta _2}{\epsilon _1}-\frac{t \left(4 \omega \alpha _1^4-3 \beta _2^2\right)}{4 \alpha _1}}\Big], \end{eqnarray}}$

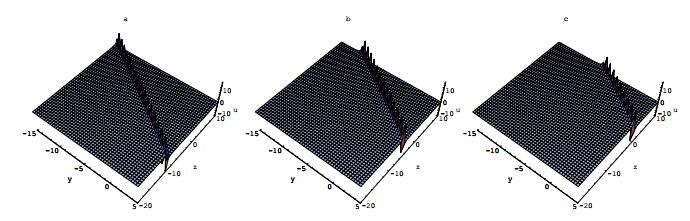
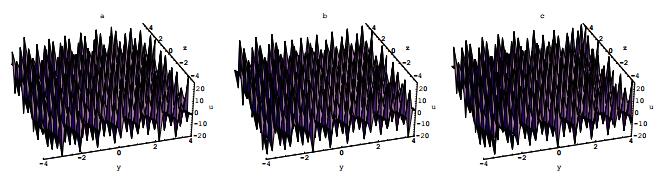
其中所有的参数在方程(2.7)中已列出.方程(2.9)的物理性质和特点被展示在图 2.

情形3

(2.10) $ {\begin{eqnarray}\delta_3& = &\frac{4 \omega \alpha _3^4+3 \beta _3^2}{4 \alpha _3}, \beta_3 = \frac{\alpha _1 \alpha _3 \beta _1\pm\sqrt{\omega \alpha _3^2 \alpha _1^6-2 \omega \alpha _3^4 \alpha _1^4+\omega \alpha _3^6 \alpha _1^2}}{\alpha _1^2}, \\ k_1 &=&k_2 = k_4=0, \delta_1=\frac{4 \omega \alpha _3^2 \alpha _1^3-3 \beta _3^2 \alpha_1+6 \alpha _3 \beta _1 \beta _3}{4 \alpha _3^2}, \end{eqnarray}} $

其中$\alpha_1$, $\alpha_3$以及$\beta_1$是任意常数.将这些参数的值代入方程(2.3),可得

(2.11) ${\begin{eqnarray}f(\eta, y, t)&=& k_3 \sinh \Big[ \eta \alpha _3+y \beta _3+\sigma_3+\frac{t \left(4 \omega \alpha _3^4+3 \beta _3^2\right)}{4 \alpha _3}\Big ]\\ &&+{\rm e}^{-\eta \alpha _1-y \beta _1-\frac{t \left(4 \omega \alpha _3^2 \alpha _1^3-3 \beta _3^2 \alpha _1+6 \alpha _3 \beta _1 \beta _3\right)}{4 \alpha _3^2}-\sigma _1}.\end{eqnarray}}$

因此,我们获得了方程(1.1)第三种形式的周期解

(2.12) ${\begin{eqnarray} u_3&= &\Big [2 \{\cosh \Big[\eta \alpha _3+y \beta_3+\sigma _3+\frac{t \left(4 \omega \alpha _3^4+3 \beta _3^2\right)}{4 \alpha _3}\Big] k_3 \alpha _3\\ &&-{\rm e}^{-\eta \alpha _1-y \beta _1-\frac{t \left(4 \omega \alpha _3^2 \alpha _1^3-3 \beta _3^2 \alpha _1+6 \alpha _3 \beta _1 \beta _3\right)}{4 \alpha _3^2}-\sigma _1} \alpha _1\}\Big]\Big/\Big[\sinh \Big [\eta \alpha _3+y \beta _3+\sigma _3\\ &&+\frac{t \left(4 \omega \alpha _3^4+3 \beta _3^2\right)}{4 \alpha _3}\Big] k_3+{\rm e}^{-\eta \alpha _1-y \beta _1-\frac{t \left(4 \omega \alpha _3^2 \alpha _1^3-3 \beta _3^2 \alpha _1+6 \alpha _3 \beta _1 \beta _3\right)}{4 \alpha _3^2}-\sigma _1}\Big], \end{eqnarray}}$

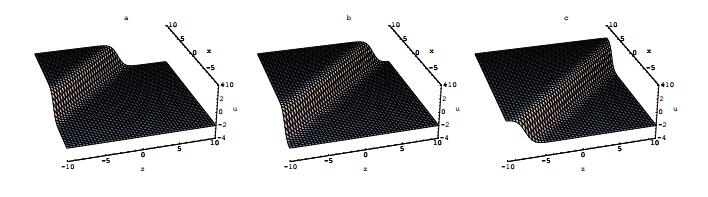
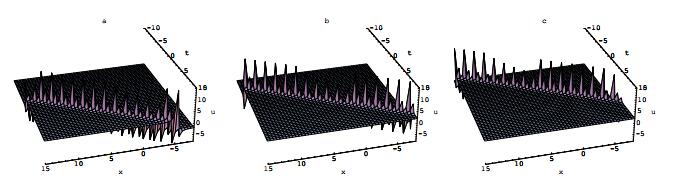
其中所有的参数在方程(2.10)中已列出.方程(2.12)的物理性质和特点被展示在图 3.

情形4

(2.13) $ {\begin{eqnarray}k_1&=&k_4=0, \alpha _3={\rm i} \alpha _2 \epsilon _2, \beta_3={\rm i} \beta _2 \epsilon _2, \delta_2 = \frac{3 \beta _2^2-4 \omega \alpha _2^4}{4 \alpha _2}, \\ \delta_1&=&\frac{4 \omega \alpha _2^2 \alpha _1^3-3 \beta _2^2 \alpha _1+6 \alpha _2 \beta _1 \beta _2}{4 \alpha _2^2}, \delta_3=\frac{{\rm i} \left(3 \beta _2^2-4 \omega \alpha _2^4\right)}{4 \alpha _2 \epsilon _2}, \\ \beta_2& = &\frac{\alpha _1 \alpha _2 \beta _1\pm\sqrt{\omega \alpha _2^2 \alpha _1^6+2 \omega \alpha _2^4 \alpha _1^4+\omega \alpha _2^6 \alpha _1^2}}{\alpha _1^2}, \end{eqnarray}}$

其中$\alpha_1$, $\alpha_2$和$\beta_1$是任意常数, $\epsilon _2=\pm1$.将这些参数的值代入方程(2.3),可得

(2.14) $ {\begin{eqnarray}f(\eta, y, t)&=&k_2 \cos \Big[\eta \alpha _2+y \beta _2+\sigma_2+\frac{t \left(3 \beta _2^2-4 \omega \alpha _2^4\right)}{4 \alpha _2}\Big]- k_3 {\rm i} \sin \Big [\frac{t \left(4 \omega \alpha _2^4-3 \beta _2^2\right)}{4 \alpha _2 \epsilon _2}\\ & &-\eta \alpha _2 \epsilon _2-y \beta _2 \epsilon _2+{\rm i} \sigma _3\Big] +{\rm e}^{-\eta \alpha _1-y \beta _1-\frac{t \left(4 \omega \alpha _2^2 \alpha _1^3-3 \beta _2^2 \alpha _1+6 \alpha _2 \beta _1 \beta _2\right)}{4 \alpha _2^2}-\sigma _1}.\end{eqnarray}}$

因此,我们获得了方程(1.1)第四种形式的周期解

(2.15) $\begin{eqnarray} u_4&=&\Big[-2 {\rm e}^{-\eta \alpha _1-y \beta_1-\frac{t \left(4 \omega \alpha _2^2 \alpha _1^3-3 \beta _2^2 \alpha _1+6 \alpha _2 \beta _1 \beta _2\right)}{4 \alpha _2^2}-\sigma _1} \alpha _1-2 k_2 \alpha _2 \sin \Big[\eta \alpha _2+y \beta _2+\sigma _2\\ & &+\frac{t \left(3 \beta _2^2-4 \omega \alpha _2^4\right)}{4 \alpha _2}\Big] + 2 k_3 \alpha _2 \epsilon _2 {\rm i} \cos \Big[\frac{t \left(4 \omega \alpha _2^4-3 \beta _2^2\right)}{4 \alpha _2 \epsilon _2}-\eta \alpha _2 \epsilon _2-y \beta _2 \epsilon _2+{\rm i} \sigma _3\Big]\Big]\\ &&\Big/\Big[{\rm e}^{-\eta \alpha _1-y \beta _1-\frac{t \left(4 \omega \alpha _2^2 \alpha _1^3-3 \beta _2^2 \alpha _1+6 \alpha _2 \beta _1 \beta _2\right)}{4 \alpha _2^2}-\sigma _1}- k_3 {\rm i} \sin \Big[\frac{t \left(4 \omega \alpha _2^4-3 \beta _2^2\right)}{4 \alpha _2 \epsilon _2} -\eta \alpha _2 \epsilon _2\\ & &-y \beta _2 \epsilon _2+{\rm i}\sigma _3\Big]+ k_2 \cos \Big[\eta \alpha _2+y \beta _2+\sigma_2+\frac{t \left(3 \beta _2^2-4 \omega \alpha _2^4\right)}{4 \alpha _2}\Big]\Big], \end{eqnarray}$

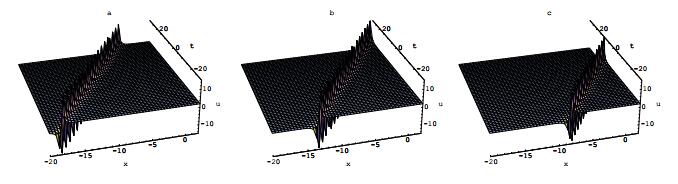
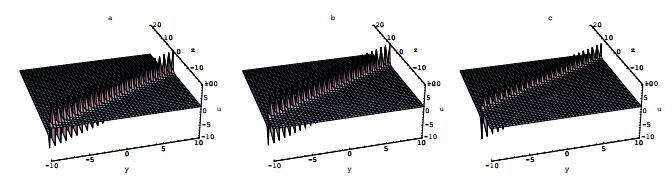
其中所有的参数在方程(2.13)中已列出.方程(2.15)的物理性质和特点被展示在图 4.

情形5

(2.16) $ {\begin{eqnarray}k_2 = k_4=0, \alpha _3=\alpha _1 \epsilon _3, \beta_3=\beta _1 \epsilon _3, \delta_3=\frac{4 \omega \alpha _3^4+3 \beta _3^2}{4 \alpha _3}, \delta_1 = \frac{4 \omega \alpha _1^4+3 \beta _1^2}{4 \alpha _1}, \end{eqnarray}}$

其中$\alpha_1$和$\beta_1$是任意常数, $\epsilon _3=\pm1$.将这些参数的值代入方程(2.3),可得

(2.17) $\begin{eqnarray}f(\eta, y, t)&=& {\rm e}^{\eta \alpha _1+y \beta _1+\sigma _1+\frac{t\left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} k_1+{\rm e}^{-\eta \alpha _1-y \beta _1-\sigma _1-\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}}\\ & &+ k_3 \sinh\Big [\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1 \epsilon _3}+\eta \alpha _1 \epsilon _3+y \beta _1 \epsilon _3+\sigma _3\Big].\end{eqnarray}$

因此,我们获得了方程(1.1)第五种形式的周期解

(2.18) $\begin{eqnarray} u_5&= &\Big [2 {\rm e}^{\eta \alpha _1+y \beta _1+\sigma _1+\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} k_1 \alpha _1+2 k_3 \epsilon _3 \alpha _1 \cosh \Big[\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1 \epsilon _3}+\eta \alpha _1 \epsilon _3\\ &&+y \beta _1 \epsilon _3+\sigma _3\Big]-2 {\rm e}^{-\eta \alpha _1-y \beta_1-\sigma _1-\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} \alpha _1\Big] \\ &&\Big/ \Big[{\rm e}^{\eta \alpha _1+y \beta _1+\sigma _1+\frac{t\left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} k_1+{\rm e}^{-\eta \alpha _1-y \beta _1-\sigma _1-\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} \\ &&+ k_3 \sinh \Big [\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1 \epsilon _3}+\eta \alpha _1 \epsilon _3 +y \beta _1 \epsilon _3+\sigma _3\Big]\Big], \end{eqnarray}$

其中所有的参数在方程(2.16)中已列出.方程(2.18)的物理性质和特点被展示在图 5.

情形6

(2.19) $\begin{eqnarray}k_4&=&0, \alpha _3=\alpha _1 \epsilon _4, \alpha_2={\rm i} \alpha _1 \epsilon _5, \beta_2={\rm i} \beta _1 \epsilon _5, \beta_3=\beta _1 \epsilon _4, \\ \delta_1&=&\frac{4 \omega \alpha _1^4+3 \beta _1^2}{4 \alpha _1}, \delta_2=\frac{{\rm i} \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1 \epsilon _5}, \delta_3=\frac{4 \omega \alpha _1^4+3 \beta _1^2}{4 \alpha _1 \epsilon _4}, \end{eqnarray}$

其中$\alpha_1$和$\beta_1$是任意常数, $\epsilon _4=\pm1$, $\epsilon _5=\pm1$.将这些参数的值代入方程(2.3),可得

(2.20) $\begin{eqnarray}f(\eta, y, t)&=& {\rm e}^{\eta \alpha _1+y \beta _1+\sigma _1+\frac{t\left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} k_1+k_3 \sinh \Big [\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1 \epsilon _4}\\ &&+\eta \alpha _1 \epsilon _4 +y \beta _1 \epsilon _4+\sigma _3\Big]+ {\rm e}^{-\eta \alpha _1-y \beta _1-\sigma _1-\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}}\\ &&+ k_2 \cosh \Big[\frac{t \left(-4 \omega \alpha _1^4-3 \beta _1^2\right)}{4 \alpha _1 \epsilon _5}-\eta \alpha _1 \epsilon _5-y \beta _1 \epsilon _5+{\rm i} \sigma _2\Big].\end{eqnarray}$

因此,我们获得了方程(1.1)第六种形式的周期解

(2.21) $\begin{eqnarray} u_6&=&\Big[-2 {\rm e}^{-\eta \alpha _1-y \beta_1-\sigma _1-\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} \alpha _1-2 k_2 \epsilon _5 \alpha _1 \sinh\Big [\frac{t \left(-4 \omega \alpha _1^4-3 \beta _1^2\right)}{4 \alpha _1 \epsilon _5}\\ &&-\eta \alpha _1 \epsilon _5-y \beta _1 \epsilon _5+{\rm i} \sigma _2\Big] + 2 {\rm e}^{\eta \alpha _1+y \beta _1+\sigma _1+\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} k_1 \alpha _1\\& & +2 k_3 \epsilon _4 \alpha _1 \cosh \Big[\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1 \epsilon _4}+\eta \alpha _1 \epsilon _4+y \beta _1 \epsilon _4+\sigma _3\Big]\Big ] \\ && \Big/\Big [k_3 \sinh\Big [\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1 \epsilon _4}+\eta \alpha _1 \epsilon _4+y \beta _1 \epsilon _4+\sigma _3\Big] \\ &&+{\rm e}^{\eta \alpha _1+y \beta _1+\sigma _1+\frac{t\left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} k_1 + {\rm e}^{-\eta \alpha _1-y \beta _1-\sigma _1-\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} \\ &&+ k_2 \cosh \Big[\frac{t \left(-4 \omega \alpha _1^4-3 \beta _1^2\right)}{4 \alpha _1 \epsilon _5}-\eta \alpha _1 \epsilon _5-y \beta _1 \epsilon _5+{\rm i} \sigma _2\Big]\Big], \end{eqnarray}$

其中所有的参数在方程(2.19)中已列出.方程(2.21)的物理性质和特点被展示在图 6.

情形7

(2.22) $\begin{eqnarray}k_1&=&k_2=k_3=0, \delta_4= \frac{3 \beta _4^2-4 \omega \alpha _4^4}{4 \alpha _4}, \delta_1=\frac{4 \omega \alpha _4^2 \alpha _1^3-3 \beta _4^2 \alpha _1+6 \alpha _4 \beta _1 \beta _4}{4 \alpha _4^2}, \\ \beta_4&=&\frac{\alpha _1 \alpha _4 \beta _1\pm\sqrt{\omega \alpha _4^2 \alpha _1^6+2 \omega \alpha _4^4 \alpha _1^4+\omega \alpha _4^6 \alpha _1^2}}{\alpha _1^2}, \end{eqnarray}$

其中$\alpha_1$, $\beta_1$以及$\alpha_4$是任意常数.将这些参数的值代入方程(2.3),可得

(2.23) $\begin{eqnarray}f(\eta, y, t)&=&k_4 \sin \Big[\eta \alpha _4+y \beta _4+\sigma_4+\frac{t \left(3 \beta _4^2-4 \omega \alpha _4^4\right)}{4 \alpha _4}\Big] \\ &&+{\rm e}^{-\eta \alpha _1-y \beta _1-\frac{t \left(4 \omega \alpha _4^2 \alpha _1^3-3 \beta _4^2 \alpha _1+6 \alpha _4 \beta _1 \beta _4\right)}{4 \alpha _4^2}-\sigma _1}.\end{eqnarray}$

因此,我们获得了方程(1.1)第七种形式的周期解

(2.24) $\begin{eqnarray} u_7&= &\Big [2\Big [\cos\Big [\eta \alpha _4+y \beta_4+\sigma _4+\frac{t \left(3 \beta _4^2-4 \omega \alpha _4^4\right)}{4 \alpha _4}\Big] k_4 \alpha _4\\ &&-{\rm e}^{-\eta \alpha _1-y \beta _1-\frac{t \left(4 \omega \alpha _4^2 \alpha _1^3-3 \beta _4^2 \alpha _1+6 \alpha _4 \beta _1 \beta _4\right)}{4 \alpha _4^2}-\sigma _1} \alpha _1\Big]\Big]\Big/\Big[\sin \Big[\eta \alpha _4+y \beta _4+\sigma _4\\ &&+\frac{t \left(3 \beta _4^2-4 \omega \alpha _4^4\right)}{4 \alpha _4}\Big] k_4+{\rm e}^{-\eta \alpha _1-y \beta _1-\frac{t \left(4 \omega \alpha _4^2 \alpha _1^3-3 \beta _4^2 \alpha _1+6 \alpha _4 \beta _1 \beta _4\right)}{4 \alpha _4^2}-\sigma _1}\Big], \end{eqnarray}$

其中所有的参数在方程(2.22)中已列出.方程(2.24)的物理性质和特点被展示在图 7.

情形8

(2.25) $\begin{eqnarray}k_1&=&k_3=0, \delta_4= \frac{3 \beta _4^2-4 \omega \alpha _4^4}{4 \alpha _4}, \delta_2=\frac{3 \beta _2^2-4 \omega \alpha _2^4}{4 \alpha _2}, \\ \delta_1&=&\frac{4 \omega \alpha _2^2 \alpha _1^3-3 \beta _2^2 \alpha _1+6 \alpha _2 \beta _1 \beta _2}{4 \alpha _2^2}, \alpha_4 = \alpha _2 \epsilon _6, \\ \beta_4& = &\beta_2 \epsilon _6, \beta_2=\frac{\alpha _1 \alpha _2 \beta_1\pm\sqrt{\omega \alpha _2^2 \alpha _1^6+2 \omega \alpha _2^4 \alpha _1^4+\omega \alpha _2^6 \alpha _1^2}}{\alpha _1^2}, \end{eqnarray}$

其中$\alpha_1$, $\beta_1$以及$\alpha_2$是任意常数, $\epsilon_6=\pm1$.将这些参数的值代入方程(2.3),可得

(2.26) $\begin{eqnarray}f(\eta, y, t)&=&{\rm e}^{-\eta \alpha _1-y \beta _1-\frac{t \left(4 \omega \alpha _2^2 \alpha _1^3-3 \beta _2^2 \alpha _1+6 \alpha _2 \beta _1 \beta _2\right)}{4 \alpha _2^2}-\sigma _1}+k_2 \cos \Big [\eta \alpha _2+y \beta _2+\sigma_2\\ &&+\frac{t \left(3 \beta _2^2-4 \omega \alpha _2^4\right)}{4 \alpha _2}\Big] + k_4 \sin\Big [\eta \alpha _2 \epsilon _6+y \beta _2 \epsilon _6+\sigma _4 +\frac{t \left(3 \beta _2^2-4 \omega \alpha _2^4\right)}{4 \alpha _2 \epsilon _6}\Big].\end{eqnarray}$

因此,我们获得了方程(1.1)第八种形式的周期解

(2.27) $\begin{eqnarray} u_8&=&\Big[-2 {\rm e}^{-\eta \alpha _1-y \beta_1-\frac{t \left(4 \omega \alpha _2^2 \alpha _1^3-3 \beta _2^2 \alpha _1+6 \alpha _2 \beta _1 \beta _2\right)} {4 \alpha _2^2}-\sigma _1} \alpha _1-2 k_2 \alpha _2 \sin \Big[\eta \alpha _2+y \beta _2+\sigma _2\\ &&+\frac{t \left(3 \beta _2^2-4 \omega \alpha _2^4\right)}{4 \alpha _2}\Big] +2 k_4 \alpha _2 \epsilon _6 \cos\Big [\frac{t \left(3 \beta _2^2-4 \omega \alpha _2^4\right)}{4 \alpha _2 \epsilon _6}+\eta \alpha _2 \epsilon _6+y \beta _2 \epsilon _6+\sigma _4\Big]\Big]\\ &&\Big/\Big[{\rm e}^{-\eta \alpha _1-y \beta _1-\frac{t \left(4 \omega \alpha _2^2 \alpha _1^3-3 \beta _2^2 \alpha _1 +6 \alpha _2 \beta _1 \beta _2\right)}{4 \alpha _2^2}-\sigma _1}+ k_4 \sin \Big[\eta \alpha _2 \epsilon _6+y \beta _2 \epsilon _6+\sigma _4\\ &&+\frac{t \left(3 \beta _2^2-4 \omega \alpha _2^4\right)}{4 \alpha _2 \epsilon _6}\Big]+ k_2 \cos \Big [\eta \alpha _2+y \beta _2+\sigma_2+\frac{t \left(3 \beta _2^2-4 \omega \alpha _2^4\right)}{4 \alpha _2}\Big]\Big], \end{eqnarray}$

其中所有的参数在方程(2.25)中已列出.方程(2.27)的物理性质和特点被展示在图 8.

情形9

(2.28) $\begin{eqnarray}\delta_1&=&\frac{4 \omega \alpha _1^4+3 \beta _1^2}{4 \alpha _1}, \delta_2= \frac{3 \beta _2^2-4 \omega \alpha _2^4}{4 \alpha _2}, \delta_3=\frac{4 \omega \alpha _3^4+3 \beta _3^2}{4 \alpha _3}, \delta_4=\frac{3 \beta _4^2-4 \omega \alpha _4^4}{4 \alpha _4}, \\ \alpha_4&=&{\rm i} \alpha _1 \epsilon _7, \beta_4={\rm i} \beta _1 \epsilon _7, \alpha_3=\alpha _1 \epsilon _8, \beta_3=\beta _1 \epsilon _8, \alpha_2={\rm i} \alpha _1 \epsilon _9, \beta_2={\rm i} \beta _1 \epsilon _9, \end{eqnarray}$

其中$\alpha_1$和$\beta_1$是任意常数, $\epsilon_7=\pm1$, $\epsilon_8=\pm1$, $\epsilon_9=\pm1$.将这些参数的值代入方程(2.3),可得

(2.29) $\begin{eqnarray} f(\eta, y, t)&=&{\rm e}^{\eta \alpha _1+y \beta _1+\sigma _1+\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} k_1+k_3 \sinh\Big [\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1 \epsilon _8}+\eta \alpha _1 \epsilon _8\\ &&+y \beta _1 \epsilon _8+\sigma _3\Big] + {\rm e}^{-\eta \alpha _1-y \beta _1-\sigma _1-\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}}+ k_2 \cosh \Big[-\eta \alpha _1 \epsilon _9\\ &&-y \beta _1 \epsilon _9+{\rm i} \sigma _2+\frac{t \left(-4 \omega \alpha _1^4-3 \beta _1^2\right)}{4 \alpha _1 \epsilon _9} \Big]- {\rm i}k_4 \sinh \Big[\frac{t \left(-4 \omega \alpha _1^4-3 \beta _1^2\right)}{4 \alpha _1 \epsilon _7}\\ &&-\eta \alpha _1 \epsilon _7-y \beta _1 \epsilon _7+{\rm i} \sigma _4\Big].\end{eqnarray}$

因此,我们获得了方程(1.1)第九种形式的周期解

(2.30) $\begin{eqnarray} u_9&= &\Big [-2 {\rm e}^{-\eta \alpha _1-y \beta_1-\sigma _1-\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} \alpha _1+2 k_3 \epsilon _8 \alpha _1 \cosh\Big [\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1 \epsilon _8}+\eta \alpha _1 \epsilon _8\\ &&+y \beta _1 \epsilon _8+\sigma _3 \Big]- 2 k_2 \epsilon _9 \alpha _1 \sinh \Big[\frac{t \left(-4 \omega \alpha _1^4-3 \beta _1^2\right)}{4 \alpha _1 \epsilon _9}-\eta \alpha _1 \epsilon _9-y \beta _1 \epsilon _9+{\rm i} \sigma _2]\\ &&+ {\rm e}^{\eta \alpha _1+y \beta _1+\sigma _1+\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} k_1 \alpha _1+ 2 {\rm i}k_4 \epsilon _7 \alpha _1 \cosh \Big[\frac{t \left(-4 \omega \alpha _1^4-3 \beta _1^2\right)}{4 \alpha _1 \epsilon _7}-\eta \alpha _1 \epsilon _7\\ &&-y \beta _1 \epsilon _7+{\rm i} \sigma _4\Big]\Big ]\Big/ \Big[{\rm e}^{\eta \alpha _1+y \beta _1+\sigma _1+\frac{t\left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} k_1 +{\rm e}^{-\eta \alpha _1-y \beta _1-\sigma _1-\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}}\\ &&+ k_2 \cosh\Big [\frac{t \left(-4 \omega \alpha _1^4-3 \beta _1^2\right)}{4 \alpha _1 \epsilon _9}-\eta \alpha _1 \epsilon _9-y \beta _1 \epsilon _9+{\rm i} \sigma _2\Big]\\ &&- {\rm i}k_4 \sinh [\frac{t \left(-4 \omega \alpha _1^4-3 \beta _1^2\right)}{4 \alpha _1 \epsilon _7}-\eta \alpha _1 \epsilon _7-y \beta _1 \epsilon _7+{\rm i} \sigma _4\Big]\\ &&+ k_3 \sinh\Big [\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1 \epsilon _8}+\eta \alpha _1 \epsilon _8+y \beta _1 \epsilon _8+\sigma _3\Big]\Big], \end{eqnarray}$

其中所有的参数在方程(2.28)中已列出.方程(2.30)的物理性质和特点被展示在图 9.

情形10

(2.31) $ {\begin{eqnarray}\delta_1&=&\frac{4 \omega \alpha _1^4+3 \beta _1^2}{4 \alpha _1}, \delta_3=\frac{4 \omega \alpha _3^4+3 \beta _3^2}{4 \alpha _3}, \delta_4=\frac{3 \beta _4^2-4 \omega \alpha _4^4}{4 \alpha _4}, \\ \alpha_3&=&\alpha _1 \epsilon _{10}, \beta_3=\beta _1 \epsilon _{10}, \alpha_4={\rm i} \alpha _1 \epsilon _{11}, \beta_4={\rm i} \beta _1 \epsilon _{11}, k_2=0, \end{eqnarray}}$

其中$\alpha_1$和$\beta_1$是任意常数, $\epsilon_{10}=\pm1$, $\epsilon_{11}=\pm1$.将这些参数的值代入方程(2.3),可得

(2.32) ${\begin{eqnarray} f(\eta, y, t)&=&{\rm e}^{\eta \alpha _1+y \beta _1+\sigma _1+\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} k_1-k_4 {\rm i} \sinh\Big [\frac{t \left(-4 \omega \alpha _1^4-3 \beta _1^2\right)}{4 \alpha _1 \epsilon _{11}}-\eta \alpha _1 \epsilon _{11}\\ &&-y \beta _1 \epsilon _{11}+{\rm i} \sigma _4\Big] + {\rm e}^{-\eta \alpha _1-y \beta _1-\sigma _1-\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}}\\ &&+ k_3 \sinh\Big [\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1 \epsilon _{10}}+\eta \alpha _1 \epsilon _{10}+y \beta _1 \epsilon _{10}+\sigma _3\Big].\end{eqnarray}}$

因此,我们获得了方程(1.1)第十种形式的周期解

(2.33) ${\begin{eqnarray} u_{10}&=&\Big[-2 {\rm e}^{-\eta \alpha _1-y \beta_1-\sigma _1-\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} \alpha _1+2 {\rm i} \cosh \Big [\frac{t \left(-4 \omega \alpha _1^4-3 \beta _1^2\right)}{4 \alpha _1 \epsilon _{11}}-\eta \alpha _1 \epsilon _{11}\\ &&-y \beta _1 \epsilon _{11}+{\rm i} \sigma _4 \Big] k_4 \epsilon _{11} \alpha _1+ 2 {\rm e}^{\eta \alpha _1+y \beta _1+\sigma _1+\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} k_1 \alpha _1\\ &&+2 \cosh\Big [\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1 \epsilon _{10}}+\eta \alpha _1 \epsilon _{10}+y \beta _1 \epsilon _{10}+\sigma _3\Big] k_3 \epsilon _{10} \alpha _1\Big]\\ && \Big/\Big [{\rm e}^{\eta \alpha _1+y \beta _1+\sigma _1+\frac{t\left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}} k_1-k_4 {\rm i} \sinh\Big [\frac{t \left(-4 \omega \alpha _1^4-3 \beta _1^2\right)}{4 \alpha _1 \epsilon _{11}}-\eta \alpha _1 \epsilon _{11}\\ &&-y \beta _1 \epsilon _{11}+{\rm i} \sigma _4\Big]+ {\rm e}^{-\eta \alpha _1-y \beta _1-\sigma _1-\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1}}\\ &&+ k_3 \sinh \Big[\frac{t \left(4 \omega \alpha _1^4+3 \beta _1^2\right)}{4 \alpha _1 \epsilon _{10}}+\eta \alpha _1 \epsilon _{10}+y \beta _1 \epsilon _{10}+\sigma _3\Big]\Big], \end{eqnarray}}$

其中所有的参数在方程(2.31)中已列出.方程(2.33)的物理性质和特点被展示在图 10.

利用Hirota双线性形式和广义三波测试法,我们列出了(3+1)维potential-YTSF方程十类多周期孤子解.一些完全新的周期孤子解被获得,其中包括了周期性交叉扭结波解、周期性双孤立波解和呼吸型双孤立波解.同时在符号计算软件Mathematica的帮助下,我们通过一些三维图形展示了这些被获得的新周期孤子解的交互作用和传播特点,从这些图形我们可以观察到两孤子间随着时间的变化的相互作用过程,包括孤立子的退化,周期分叉现象,呼吸二波的裂变与融合等.孤子相互作用现象清楚的展示在在图 1-10中,有非常重要的物理意义.