1 引言
众所周知,稳定性是系统理论研究的主要问题之一.在时滞系统稳定性的研究中, Lyapunov-Razumikhin方法是最有效的研究方法之一. Razumikhin在文献[7-8]中研究确定性时滞系统的稳定性时最早提出了这种方法.随后,毛等将这种方法推广到了随机泛函微分系统[9],在研究随机时滞微分系统的
在上述文献中,研究者主要研究了随机时滞非线性系统和中立型随机非线性系统的
本文的主要内容安排如下:第2节给出问题的描述及本文所用到的预备知识;第3节利用Lyapunov-Razumikhin型方法给出并证明中立型随机切换非线性系统
2 预备知识
首先给出本文用到的一些记号.
考虑一族中立型随机切换非线性系统
其中
对于解的存在唯一性我们作如下假设
假设2.1[18] 函数
对
且函数
定义2.1[18]
(1) 该函数单调递减且连续可微;
(2)
(3)
(4) 对于所有的
定义2.2 对于
当
定义2.3 中立型随机切换非线性系统(2.1)称为几乎必然
当
在给出本文引理之前,先介绍本文所用的
对于系统(2.1),任给函数
为便于本文定理的推导,记
引理2.1[14] 对于任意常数
则对于任意初始值
证 由
由基本不等式,条件(2.4)和函数
由
由
证毕.
引理2.2[9] (Burkholder-Davis-Cundy不等式) 当
其中
引理2.3[9] (Borel-Cantelli引理)
(1) 若
即存在集合
(2) 若序列
即存在集合
3 主要结果及证明
本节采用Razumikhin技术和Lyapunov函数建立中立型随机切换非线性系统的
定理3.1 对于中立型随机切换非线性系统(2.1),若假设2.1成立,当
且存在正常数
对
其中
其中
则对任意初始值
证 给定任意初始值
给定任意时刻
对
即等价于证
由引理2.1可知,只需证
即等价于证
由(3.2)式可知
即等价于证对
下证对
由
首先证
采用反证法.假设(3.10)式不成立,由
其中
故,对
由(3.3)式得
对
由(3.3)式可知
这与假设矛盾.因此,对
令
下证
令
采用反证法.假设(3.14)式不成立,由(3.5)和(3.15)式,可得
即
由
其中
故,对
由(3.3)式,可得
对
由(3.3)式,可知
这与假设矛盾.故对
由数学归纳法,对
定理3.2 对于中立型随机切换非线性系统(2.1),假设定理3.1的所有条件均成立,即存在常数
且存在常数
对
则对任意初始值
证 对任意初始值
其中
由于
选取充分小的
由
其中
由Holder不等式, (3.20)式, (3.21)式和
类似地,由Holder不等式,引理2.2和(3.21)式,得
其中
把(3.31)式代入(3.26)式得
令
其中
由(3.22)式和引理2.3,可知,当
即
注3.2 定理3.2给出并证明了中立型随机切换非线性系统(2.1)的几乎必然
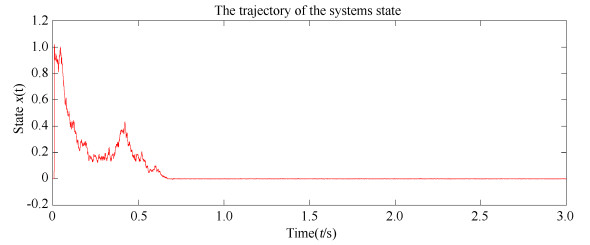
4 仿真算例
本节通过一个具体的算例验证上一节主要定理的有效性.
考虑一族中立型随机切换非线性系统
其中
选取
当
对于第一个子系统,选取
若
对于第二个子系统,选取
若
图 1
图 2
5 结论
本文究了中立型随机切换非线性系统的
参考文献
On stability of switched stochastic systems
Stability analysis of switched stochastic systems
DOI:10.1016/j.automatica.2010.10.023 [本文引用: 1]
Stability and H∞ performance analysis of switched stochastic neutral systems
DOI:10.1007/s00034-012-9459-1 [本文引用: 1]
Exponential stability for neutral stochastic markov systems with time varying delay and its applications
DOI:10.1109/TCYB.2015.2442274 [本文引用: 2]
Application of Lyapunov's method to problems in the stability of systems with a delay
Razumikhin-type theorems on exponential stability of stochastic functional differential equations
DOI:10.1016/S0304-4149(96)00109-3 [本文引用: 1]
Razumikhin-type theorems on exponential stability of neutral stochastic functional differential equations
DOI:10.1137/S0036141095290835 [本文引用: 2]
Razumikhin-type theorems on exponential stability of stochastic functional differential equations with infinite delay
Razumikhin-type theorems on general decay stability of stochastic functional differential equations with infinite delay
DOI:10.1016/j.cam.2011.09.045 [本文引用: 1]
Razumikhin-type theorem for neutral stochastic functional differential equations with unbounded delay
Global exponential stability of impulsive stochastic functional differential systems
P-th moment stability of impulsive stochastic delay differential systems with markovian switching
DOI:10.1016/j.cnsns.2012.12.001
Some criteria on p-th moment stability of impulsive stochastic functional differential equations
Razumikhin-type theorems on general decay stability and robustness for stochastic functional differential equations
Stability analysis of deterministic and stochastic switched systems via a comparison principle and multiple Lyapunov functions
DOI:10.1137/040619429 [本文引用: 1]