1 引言
Rossby波是很重要的大尺度波动.在近几年中,在许多大规模尺度运动中,非线性Rossby波受到了大气海洋领域的高度重视. Long[1]在20世纪60年代发现了切变纬向流中的Rossby孤立波.然后Benney[2], Redekopp[3]和其他学者推广了Long的结论.在20世纪70-80年代非线性Rossby孤立波的相关理论得到了飞速的发展.对于Rossby孤立波,许多研究者研究了一些弱非线性模型.其中, Korteweg-de Vries (KdV)方程[4-6]常用来描述经典Rossby孤立波的.对于包络Rossby孤立波,非线性Rossby波的非线性Schrödinger(NLS)首先分别由Benney[7]和Yamagata[8]得到.之后,由于其广泛和重要的应用,许多研究人员已经致力于在理论和数值上研究该方程[9-16].例如, Liao[17]提出了变系数非线性薛定谔方程的变分积分方程. Chen[18]利用时空伸长变化与摄动法描述了耦合非线性薛定谔方程的一种新的精确解. Yao[19]描述了一些具有实际电位的线性和非线性薛定谔方程的均匀性. Li[20]导出了
另一方面,地球自转对地球流体力学中的许多现象也有显著的影响,它的作用是通过流体动力学Navier-Stokes方程中出现额外加速度项
2 模型和方法
无量纲的正压位涡方程的形式[33]如下
其中引入了两个无量纲参数
边界条件为
平均流函数
我们引进一个小参数
其中
将方程(2.4)代入方程(2.1),得
引入缓变量
则
将方程(2.7)带入方程(2.5),得到
其中线性算子
边界条件为
显然,对于偶极子结构,方程(2.8)的解可以表示为
其中,
将方程(2.10)代入方程(2.8)中,得到
方程(2.11)的解可以写成
其中
其中方程(2.13)中的系数请参照附录A.
将方程(2.10), (2.12)和(2.13)代入到方程(2.14)中,要想不含
其中的系数
3 Rossby波列的调制不稳定性
在这一节中,我们来研究Rossby波列的调制不稳定性.方程(2.15)中的振幅取如下形式
将方程(3.1)代入方程(2.15)中,得到
其中
我们将
将方程(3.3)代入到方程(3.2),得到关于
由于调制的周期性,我们取如下形式
其中
1)若
其中
我们定义
其中
2)若
其中
我们定义
这里
方程(3.15)的解为
在方程(3.18)中,当
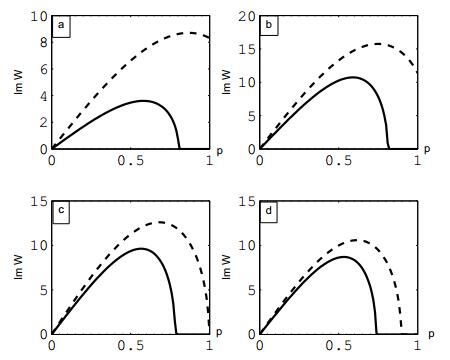
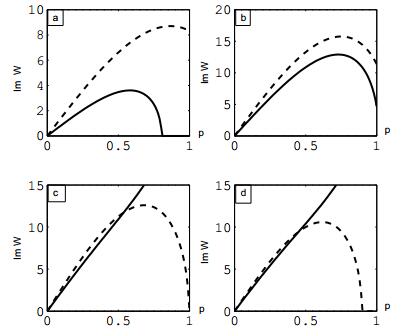
图 1
图 1
在北纬60度,横坐标取
图 2
图 2
在北纬60度,横坐标取
第一种情形:从图 1中我们可以看到,在北纬60度下,当
第二种情形:从图 2中我们可以看出,在北纬60度下,当
4 结论
在本文中,应用了摄动展开的方法推导了在含有地形项作用和完整Coriolis力作用下的一类高阶Schrödinger方程(HNLS方程).基于此方程,讨论了均匀Rossby波列的调制不稳定性.我们可以得到完整Coriolis力下的高阶项
附录A
方程(2.13)的系数可以定义为
附录B
方程(2.15)的系数可以定义为
参考文献
Solitary waves in the Westerlies
DOI:10.1175/1520-0469(1964)021<0197:SWITW>2.0.CO;2 [本文引用: 1]
Long nonlinear waves in fluid flows
DOI:10.1002/sapm196645152 [本文引用: 1]
On the theory of solitary Rossby waves
DOI:10.1017/S0022112077000950 [本文引用: 1]
Equatorial solitary waves. Part Ⅰ:Rossby solitons
DOI:10.1175/1520-0485(1980)010<1699:ESWPIR>2.0.CO;2 [本文引用: 1]
Evolution equations for long, nonlinear internal waves in stratified shear flows
Forced solitary Rossby waves under the influence of slowly varying topography with time
DOI:10.1088/1674-1056/20/12/120201 [本文引用: 1]
Large amplitude Rossby waves
DOI:10.1002/sapm.v60.1 [本文引用: 1]
The stability, modulation and long wave resonance of a planetary wave in a rotating, two-layer fluid on a channel beta-plane
DOI:10.2151/jmsj1965.58.3_160 [本文引用: 2]
Numerical solution of the Gross-Pitaevskii equation for Bose-Einstein condensation
DOI:10.1016/S0021-9991(03)00102-5 [本文引用: 1]
Mathematical theory and numerical methods for Bose-Einstein condensation Kinet
Exponential time differencing Crank-Nicolson method with a quartic spline approdinger for nonlinear Schrödinger equations
Solving the generalized nonlinear Schröginger equation via quartic spline approximation
The existence of nontrivial solutions for a class of asymtotically linear equation
Ground state sulutions for periodic Schrödinger equation with critical sobolev exponent
Mountain pass solutions for fractional coupled nonlinear Schrödinger systems
Numerical simulation of Rogue waves by the local discontinuous galerkin method
DOI:10.1088/0256-307X/31/4/040201 [本文引用: 1]
Muilti-symplectic variational integrators for nonlinear Schrödinger equations with variable coefficients
DOI:10.1088/1674-1056/25/1/010205 [本文引用: 1]
Novel exact solutions of coupled nonlinear Schrödinger equations with time-space modulation
Homogenization of some linear and semilinear Schrödinger equations with real potential
(2+1)-dimensional dissipation nonlinear Schrödinger equation for envelope Rossby solitary waves and chirp effect
DOI:10.1088/1674-1056/25/4/040202 [本文引用: 1]
Derivation of a higher order nonlinear Schrödinger equation for weakly nonlinear Rossby waves
DOI:10.1016/S0165-2125(00)00073-1 [本文引用: 3]
Kuznetsov-Masoltion and Akhmediev breather of high-order nonlinear Schrödinger equation
DOI:10.1088/1674-1056/25/1/010507 [本文引用: 1]
The equations of motion for a shallow rotating atmosphere and 'traditional approximation'
DOI:10.1175/1520-0469(1966)023<0626:TEOMFA>2.0.CO;2 [本文引用: 1]
Comments on Phillips' (1966) proposed simplification of the equations of motion for shallow rotating atmosphere
DOI:10.1175/1520-0469(1968)025<1154:COPPSO>2.0.CO;2
Comment on "The equations of motion for a shallow rotating atmosphere and the 'traditional approxmation'"
DOI:10.1175/1520-0469(1970)027<0504:COEOMF>2.0.CO;2 [本文引用: 1]
The influence of the horizonal component of the Erath's angular velocity on the instability of the Ekman layer
DOI:10.1017/S0022112085000039 [本文引用: 1]
Non-hydrostatic Coriolis effects in an isentropic coordinate frame
Unsymmetrical symmetric instability
DOI:10.1002/(ISSN)1477-870X [本文引用: 1]
Dynamically consistent, quasi-hydrostatic equations for global models with a complete representation of the Coriolis force
DOI:10.1002/(ISSN)1477-870X [本文引用: 1]
The potential vorticity equation:from planetary to small scale
完整Coriolis力作用下非线性Rossby波的精确解
DOI:10.3321/j.issn:0001-5733.2008.05.004 [本文引用: 1]
Exact solutions to the nonlinear Rossby waves with a complete representation of the Coriolis force
DOI:10.3321/j.issn:0001-5733.2008.05.004 [本文引用: 1]
缓变地形下β效应的Rossby代数孤立波
Algebraic solitary Rossby waves excited slowly changing topography and beta effect
Shallow water equations with a copplete Coriolis force and topography
The stability of small amplitude Rossby waves in a channel