种群生态学是研究控制生物种群量与其栖境关系的一门学科^[1].法国数学家Poincare创立了微分方程定性理论^[2].国内外的生物数学家利用微分方程定性理论在种群生态学领域取得了比较多的研究成果.由于生态系统的复杂和多样性,为了更准确的描述和刻画现实世界,科学家们将时滞引入到微分方程中对生态系统进行研究.捕食者与猎物的关系是自然界中生物种群相互作用的基本作用之一,关于它的各种情况的研究,很多学者做了大量的工作,也取得了不小的进展.如张天然在模型中加入了猎物性别因素^[3],张丽红考虑到年龄结构的影响^[4],这些因素的加入弥补了以前捕食者-猎物系统对种群内部相异性思考不足的情况,使得捕食者-猎物系统与现实的相符程度比之从前更进一步.

在捕食者-猎物-共生系统方面的研究相对较少, BindhyachalRai等在文献[5-8]中深入探讨了捕食者-猎物-共生者系统的Hopf分支,并进行了数值模拟,我国的田灿荣则研究了捕食者-猎物-共生者系统的图灵模式^[6],可见,该方面还有很广阔的研究空间.

本文主要研究基于瓢虫、棉蚜和蚂蚁的捕食者-猎物-共生者系统,考虑到昆虫的时滞的影响更为显著,因此本文研究了具有时滞的捕食者-猎物-共生者系统,通过对模型的分析,了解瓢虫、棉蚜和蚂蚁之间的制约关系,为棉田的生态调节提供一定的理论依据.

正性

定义2.1^[9]  系统

(2.1) $ \left\{\begin{array}{ll} \dot x_{1}=g_{1}(t, x_{1}, x_{2}, x_{3}), \\ \dot x_{2}=g_{2}(t, x_{1}, x_{2}, x_{3}), \\ \dot x_{3}=g_{3}(t, x_{1}, x_{2}, x_{3}). \end{array}\right. $

系统(2.1)的解的正性是指当初值$x_{i}(0)>0$$(i=1, 2, 3)$时,对任意$t>0, x_{i}(t)>0$$(i=1, 2, 3)$皆成立.

持久性

定义2.2^[10]  系统(2.1)持久性是指存在一个紧集$K\subset {\rm Int}{\mathbb{R}}^3_{+}$,使得对每一个具有正初始值的解$X(t)=\{x_{1}(t), x_{2}(t), x_{3}(t)\}$最终进入并保持在$K$中.即存在正整数$m_{i}\ (i=1, 2, 3)$和$M_{i}\ (i=1, 2, 3)$,对于系统的正解$X(t)=\{x_{1}(t), x_{2}(t), x_{3}(t)\}$有

$m_{i}\leqslant\lim\limits_{t\to\infty}\inf x_{i}(t)\leqslant\lim\limits_{t\to\infty}\sup x_{i}(t)\leqslant M_{i} (i=1, 2, 3).$

可以这样理解持久性,即生态系统在一定边界范围内保持恒定或维持某一特定状态的持续时间.

平衡点局部稳定性的判定

设种群、群落或生态系统的动力系统模型由微分方程表示,用向量形式写为

(2.2) $\frac{{\rm d}x}{{\rm d}t}=f(x), $

其中状态向量$x=(x_{1}, x_{2}, \cdots , x_{n})^T, \dot x=(\dot x_{1}, \dot x_{2}, \cdots , \dot x_{n})^T, f(x)=(f_{1}(x), f_{2}(x), \cdots , f_{n}(x))^T$.

特征值的分析是稳定性分析的关键,对于非线性微分方程,可先将其线性化,列出其特征方程,然后进行讨论.

定理2.1^[11]  平衡点$x^*$渐近稳定的充分条件是系统(2.2)的特征方程的所有特征值具有负实部,即

${\rm Re}\lambda_{i}(A)<0, \;\;\;\;i=1, 2, \cdots , n.$

反之,如果特征方程具有正实部的特征值,那么$x^*$就是不稳定的.对与具体的三次方程由Hurwitz判据^[9],有如下判据:实系数三次方程

$\lambda^3+a_{1}\lambda^2+a_{2}\lambda+a_{3}=0$

的一切均有负实部的充要条件是$a_{1}>0, a_{3}>0, a_{1}a_{2}-a_{3}>0$.

定理2.2^[10]  关于方程$(z+a)e^z+b=0$的所有根, $a$和$b$都是实数,当方程的根全都有负实部时,有且只有如下条件成立

$a>-1;\;\;\;\; a+b>0; \;\;\;\;b<\xi \sin\xi-a \cos\xi, $

此时第三个条件也可写为

$b<\sqrt{a^2+\xi^2}, $

其中$\xi>0$.

根据文献^[5]中的模型,本文主要建立并研究系统

(3.1) $ \left\{\begin{array}{ll} \frac{{\rm d}x}{{\rm d}t}=r_{1}x(1-\frac{x(t-\tau_{1})}{K})-\frac{\beta xy(t-\tau_{2})}{1+mu}, \\[3mm] \frac{{\rm d}u}{{\rm d}t}=r_{2}u(1-\frac{u}{l_{0}+lx}), \\[3mm] \frac{{\rm d}y}{{\rm d}t}=-sy+\frac{c\beta xy(t-\tau_{2})}{1+mu}. \end{array}\right. $

该系统的各个参数生物学意义如下: $x(t)$表示猎物(棉蚜)的种群密度, $u(t)$表示共生者(蚂蚁)的种群密度, $y(t)$表示捕食者(瓢虫)的种群密度, $r_{1}$表示猎物的内禀增长率(理想状态下种群的最大瞬时增长率), $r_{2}$表示共生者的内禀增长率, $\tau_{1}$表示猎物的发育时间, $\tau_{2}$表示捕食者的发育时间, $K$表示猎物的最大环境容纳量, $\beta$表示捕食者对猎物的捕食率(单位时间内每个捕食者对猎物的捕获量与猎物种群规模之间的比例), $m$表示共生者对猎物的效应系数, $l_{0}$表示在缺少周围的捕食者的情况下共生者的最大容纳量, $l$表示猎物对共生者的效应系数,可以这样认为:猎物$x(t)$的存在增强共生者$u(t)$数量的承载能力,承载能力用$l_{0}+lx$表示, $l_{0}$表示共生者数量在没有捕食者的环境承载能力, $s$表示捕食者的自然死亡率, $c$表示捕食者对猎物的转化率.

本部分主要对模型的正性,持久性和局部稳定性进行分析.系统(3.1)满足初始条件(4.1)和(4.2).

(4.1) $当- {\tau _1}<t<0时,\;\;有x(t) = \varphi(t) > 0.$

(4.2) $当- {\tau _2}<t<0时,\;\;有y(t) = \phi (t) > 0.$

定理4.1  如果系统满足初始条件,则当$t>0$时,有$x(t)>0, y(t)>0, z(t)>0$.

证  由系统(3.1)可知

$x(t)=\exp\bigg\{\int_0^t\bigg[r_{1}(1-\frac{x(f-\tau_{1})}{K})-\frac{\beta y(f-\tau_{2})}{1+mu}\bigg]{\rm d}f\bigg\}x(0)>0, $

$u(t)=\exp\bigg\{\int_0^t\bigg[r_{2}(1-\frac{u}{l_{0}+lx})\bigg]{\rm d}t\bigg\}u(0)>0. $

对于第三个式子,首先假设当$t\in(0, \tau_{2})$时存在第一个时间点$t_{i}$,满足$y(t_{i})=0$.利用初始条件(4.2),可以看出$y(t_{i}-\tau_{2})=\phi(t_{i})>0$,代入系统(3.1),得

$\frac{{\rm d}y}{{\rm d}t}\bigg|_{t=t{i}}=-sy(t_{i})+\frac{c\beta xy(t_{i}-\tau_{2})}{1+mu}>0.$

即在$t\in(0, \tau_{2})$时$y(t)$为上升走向,与$y(t_{i})=0$不符,假设不成立,即在$t\in(0, \tau_{2})$时$y(t)>0$.同样在$t\in(\tau_{2}, 2\tau_{2})$中假设存在点$(t_{i+1}, y_{i+1}), y_{i+1}\leqslant0$,此时

$\frac{{\rm d}y}{{\rm d}t}\bigg|_{t=t_{i+1}}=-sy(t_{i+1})+\frac{c\beta xy(t_{i+1}-\tau_{2})}{1+mu}>0.$

即在$t\in(\tau_{2}, 2\tau_{2})$时$y(t)$为上升走向,与$y(t_{i+1})=0$不符,假设不成立,即在$t\in(\tau_{2}, 2\tau_{2})$时$y(t)>0$.以此类推,可得出对$t>0, y(t)>0$.

综上,当初始条件(4.1)和(4.2)成立,所以当$t>0$时, $x(t)>0, y(t)>0, z(t)>0$恒成立,证明完毕.

记

$ M_{1}=K\exp\{r_{1}\tau_{1}\}, \;\;\;\;M_{2}=l_{0}+lM_{1}, \;\;\;\;M=M_{1}(r_{1}c+sc), \;\;\;\;M_{3}=\frac{M}{s}. $

$ m_{1}=\frac{K(r_{1}-\beta M_{3})}{r_{1}}\exp\bigg\{(r_{1}-\frac{r_{1}}{K}M_{1}-\beta M_{3})\tau_{1}\bigg\}, \;\;\;\;m_{2}=l_{0}+lm_{1}, $

$ m=m_{1}\bigg[(r_{1}c+sc)-\frac{r_{1}cM_{1}}{K}\bigg], \;\;\;\;m_{3}=\frac{m}{s}-cM_{1}. $

并记

${\rm (A1)} K\exp\{r_{1}\tau_{1}\}(r_{1}c+sc)<\frac{r_{1}s}{\beta};\;\;\;\;\;{\rm (A2)} \exp\{r_{1}\tau_{1}\}<\min\bigg\{1+\frac{s}{r_{1}}, \frac{(r_{1}+s)m_{1}}{sK+r_{1}m_{1}}\bigg\}.$

定理4.2  若系统(3.1),满足条件(A1)和(A2),则系统(3.1)具有持久性.

证  因为

$\frac{{\rm d}x}{{\rm d}t}=r_{1}x(1-\frac{x(t-\tau_{1})}{K})-\frac{\beta xy(t-\tau_{2})}{1+mu}\leqslant r_{1}x(1-\frac{x(t-\tau_{1})}{K})=x(r_{1}-\frac{r_{1}x(t-\tau_{1})}{K}). $

利用文献[10]中的方法,可知存在$T_{1}>\tau_{1}+\tau_{2}$,使得$t>T_{1}$时,有

$x(t)\leqslant K\exp\{r_{1}\tau_{1}\}=M_{1}. $

因为

$\frac{{\rm d}u}{{\rm d}t}=r_{2}u(1-\frac{u}{l_{0}+lx})\leqslant r_{2}u(1-\frac{u}{l_{0}+lM_{1}})=u(r_{2}-\frac{r_{2}u}{l_{0}+lM_{1}}), $

于是存在$T_{2}>T_{1}$,当$t>T_{2}$,有$u(t)\leqslant l_{0}+lM_{1}=M_{2}$.

因为$x(t)$有上界,故存在$M>0$,使$x[(r_{1}c+sc)-\frac{r_{1}cx(t-\tau_{1})}{K}]\leqslant M$.从而使

$\begin{eqnarray*}\frac{{\rm d}(cx+y)}{{\rm d}t}&=&r_{1}cx(1-\frac{x(t-\tau_{1})}{K})-sy\\&=& x\bigg[(r_{1}c+sc)-\frac{r_{1}cx(t-\tau_{1})}{K}\bigg]-s(cx+y)\\&\leqslant&M-s(cx+y).\end{eqnarray*}$

于是存在$T_{3}>T_{2}+\tau_{1}$,当$t>T_{3}$时,有$cx+y\leqslant \frac{M}{s}, y(t)\leqslant \frac{M}{s}=M_{3}$.又

$\frac{{\rm d}x}{{\rm d}t}=r_{1}x(1-\frac{x(t-\tau_{1})}{K})-\frac{\beta xy(t-\tau_{2})}{1+mu}\geqslant r_{1}x(1-\frac{x(t-\tau_{1})}{K})-\beta xM_{3}.$

根据文献[11],可以得出,若条件(A1)成立,存在$T_{4}>T_{3}+\tau_{2}$,使得$t>T_{4}$时,有

$x(t)\geqslant \frac{K(r_{1}-\beta M_{3})}{r_{1}}\exp\bigg\{(r_{1}-\frac{r_{1}}{K}M_{1}-\beta M_{3})\tau_{1}\bigg\}=m_{1}.$

因为$\frac{{\rm d}u}{{\rm d}t}=r_{2}u(1-\frac{u}{l_{0}+lx})\geqslant r_{2}u(1-\frac{u}{l_{0}+lm_{1}})$,可以得出,存在$T_{5}>T_{4}$,使得$t>T_{5}$时,有$u(t)\leqslant l_{0}+lm_{1}=m_{2}$.

由于$x(t)\geqslant m_{1}$,当条件(A2)成立时,存在$m=m_1[(r_{1}c+sc)-\frac{r_{1}cM_{1}}{K}]>0$,使$x[(r_{1}c+sc)-\frac{r_{1}cx(t-\tau_{1})}{K}]\geqslant m$.从而

$\begin{eqnarray*}\frac{{\rm d}(cx+y)}{{\rm d}t}&=&r_{1}cx(1-\frac{x(t-\tau_{1})}{K})-sy\\&=&x\bigg[(r_{1}c+sc)-\frac{r_{1}cx(t-\tau_{1})}{K}\bigg]-s(cx+y)\\&\geqslant&m-s(cx+y).\end{eqnarray*}$

于是存在$T_{6}>T_{5}$,当条件(A2)成立时,使得$t>T_{6}$时,有

$cx+y\geqslant {m}{s}, \;\;\;\;y(t)\geqslant {m}{s}-cM_{1}=m_{3},\;\;\;\; m_{3}>0.$

综上所述,若条件(A2)成立,则存在$T=\max\limits_{i=1, \cdots , 6}\{T_{i}\}$,使得$t>T$时,有

$m_{1}\leqslant x(t)\leqslant M_{1}, \;\;\;\;m_{2}\leqslant u(t)\leqslant M_{2}, \;\;\;\;m_{3}\leqslant x(t)\leqslant M_{1}, $

其中$M_{1}, M_{2}, M_{3}, m_{1}, m_{2}, m_{3}$均大于$0$,持久性得证.

系统(3.1)的平衡点有

$E_{1}(0, 0, 0), E_{2}(0, l_{0}, 0), E_{3}(K, 0, 0), E_{4}(x^*_{1}, 0, y^*_{1}), E_{5}(K, l_{0}+lK, 0), E_{6}(x^*_{2}, u^*_{2}, y^*_{2}), $

其中

$x^*_{1}=\frac{s}{c\beta}, y^*_{1}=\frac{r_{1}}{\beta}(1-\frac{s}{c\beta K}), x^*_{2}=\frac{s+sml_{0}}{c\beta -sml}, u^*_{2}=l_{0}+lx^*_{2}=\frac{c\beta l_{0}+ls}{c\beta -sml}, $

$y^*_{2}=\frac{r_{1}}{\beta}(1-\frac{x^*_{2}}{K})(1+mu^*_{2})=\frac{r_{1}c}{K}\frac{(c\beta K-smlK-s-sml_{0})(1+l_{0}m)}{(c\beta -sml)^2}.$

下面分别讨论这些平衡点的局部稳定性,对系统(3.1)在各个平衡点进行线性化,从而得出该方程平衡点$(x^*, u^*, y^*)$的特征方程为

(4.3) $\left|\begin{array}{ccc}\begin{array}{c} r_{1}(1-\frac{x^*}{K})-\frac{\beta y^*}{1+mu^*}\\[2mm] -\frac{r_{1}x^*}{K}\exp\{-\lambda\tau_{1}\}-\lambda\end{array}& \frac{m\beta x^*y^*}{(mu^*+1)^2}& -\frac{\beta x^*}{1+mu^*}\exp\{-\lambda\tau_{2}\} \\ \frac{r_{2}(u^*)^2l}{(l_{0}+lx^*)^2}& r_{2}-\frac{2r_{2}}{l_{0}+lx^*}u^*-\lambda&0\\ \frac{c\beta y^*}{1+mu^*}& -\frac{c\beta x^*y^*m}{(1+mu^*)^2}& -s+\frac{c\beta x^*}{1+mu^*}\exp\{-\lambda\tau_{2} \}-\lambda \end{array}\right|=0. $

将$E_{1}(0, 0, 0), E_{2}(0, l_{0}, 0), E_{3}(K, 0, 0), E_{4}(x^*_{1}, 0, y^*_{1})$代入上面的特征方程中,由定理2.1,不难得到

定理4.3  平衡点$E_{1}, E_{2}, E_{3}, E_{4}$都不稳定.

定理4.4  若条件(A3): $s>\frac{c\beta K}{1+m(l_{0}+lK)}$成立,则平衡点$E_{5}(K, l_{0}+lK, 0)$是局部渐近稳定的.

证  平衡点$E_{5}(K, l_{0}+lK, 0)$对应的特征方程为

(4.4) $\left|\begin{array}{ccc} -r_{1}\exp\{-\lambda\tau_{1}\}-\lambda&0& -\frac{\beta K}{1+m(l_{0}+lK)}\exp\{-\lambda\tau_{2}\}\\[3mm]r_{2}l&-r_{2}-\lambda&0\\[3mm]0&0& -s+\frac{c\beta K}{1+m(l_{0}+lK)}\exp\{-\lambda\tau_{2}\}-\lambda\end{array}\right|=0.$

整理得

$(-s+\frac{c\beta K}{1+m(l_{0}+lK)}\exp\{-\lambda\tau_{2}\}-\lambda)(-r_{1}\exp\{-\lambda\tau_{1}\}-\lambda)(-r_{2}-\lambda)=0, $

其中$(-r_{2}-\lambda)$中的$\lambda=-r_{2}<0$,而在$(-r_{1}\exp\{-\lambda\tau_{1}\}-\lambda)$中$\lambda=-r_{1}\exp\{-\lambda\tau_{1}\}$,因为$\exp\{-\lambda\tau_{1}\}$一定大于$0$, $-r_{1}\exp\{-\lambda\tau_{1}\}$一定小于$0$,所以$\lambda<0$.

下面分析

(4.5) $-s+\frac{c\beta K}{1+m(l_{0}+lK)}\exp\{-\lambda\tau_{2}\}-\lambda=0.$

把(4.5)变成以下的形式

$(\lambda\tau_{2}+s\tau_{2})\exp\{\lambda\tau_{2}\}-\frac{c\beta K}{1+m(l_{0}+lK)}\tau_{2}=0.$

当条件(A3)条件成立时,该平衡点$E_{5}$局部渐近稳定.

记

$\begin{eqnarray*}{\rm (A4)}~ &&c\beta-sml>0;\;\;\;\; {\rm (A5)}~ c\beta K-amlK>s+sml_{0};\\[2mm]{\rm (A6)}~ && (r_{1}\frac{s+sml_{0}}{c\beta K-smlK}+r_{2})\bigg[r_{1}s(\frac{r_{2}}{s}A+\frac{mlr_{2}}{c\beta}A-\frac{mlr_{2}}{c\beta}+1-A)\bigg]\\&&-\bigg[sr_{1}r_{2}(\frac{sml}{c\beta}-1)(A-1)\bigg]>0.\end{eqnarray*}$

定理4.5  在$\tau_{1}=0, \tau_{2}=0$的情况下,如果满足条件(A4)-(A6),则正平衡点$E_{6}$是局部渐近稳定的.

证  对正平衡点$E_{6}(x^*_{2}, u^*_{2}, y^*_{2})$,其中

$x^*_{2}=\frac{s+sml_{0}}{c\beta-sml}, \;\;\;\;u^*_{2}=l_{0}+lx^*_{2}=\frac{c\beta l_{0}+ls}{c\beta-sml}.$

$y^*_{2}=\frac{r_{1}}{\beta}(1-\frac{x^*_{2}}{K})(1+mu^*_{2})=\frac{r_{1}c}{K}\frac{(c\beta K-smlK-s-sml_{0})(1+l_{0}m)}{(c-\beta-sml)^2}.$

相应的特征方程整理得

(4.6) $\left|\begin{array}{ccc} -\frac{r_{1}x^*_{2}}{K}\exp\{-\lambda\tau_{1}\}-\lambda& \frac{mr_{1}s}{c\beta}(1-\frac{x^*_{2}}{K}) & -\frac{s}{c}\exp\{-\lambda\tau_{2}\}\\[2mm]r_{2}l&-r_{2}-\lambda&0\\[2mm] cr_{1}(1-\frac{x^*_{2}}{K})& -\frac{mr_{1}s}{\beta}(1-\frac{x^*_{2}}{K})& -s+s\exp\{-\lambda\tau_{2}\}-\lambda\end{array}\right|=0.$

设$A=\frac{x^*_{2}}{K}=\frac{s+sml_{0}}{c\beta K-smlK}$,将$A$代入(4.6)式,得到结果

$\begin{eqnarray*}&&\lambda^3(-1)+\lambda^2(-r_{1}A\exp\{-\lambda\tau_{1}\}-r_{2}-s+s\exp\{-\lambda\tau_{2}\})+\lambda(-r_{1}r_{2}A\exp\{-\lambda\tau_{1}\}\\&&-r_{1}As\exp\{-\lambda\tau_{1}\}+r_{1}As\exp\{-\lambda\tau_{1}-\lambda\tau_{2}\}+\frac{msr_{1}r_{2}l}{\beta c}-\frac{msr_{1}r_{2}lA}{\beta c}\\&&+sr_{1}A\exp\{-\lambda\tau_{2}\}-sr_{1}\exp\{-\lambda\tau_{2}\}+r_{2}s\exp\{-\lambda\tau_{2}\}-r_{2}s)\\&&+\Big[-r_{1}r_{2}As\exp\{-\lambda\tau_{1}\}+r_{1}r_{2}As\exp\{-\lambda\tau_{1}\}\exp\{-\lambda\tau_{2}\}\\&&+\frac{mslr_{1}r_{2}}{\beta c}(s-s\exp\{-\lambda\tau_{1}\}-As+As\exp\{-\lambda\tau_{2}\})+\frac{s^2lmr_{1}r_{2}}{c\beta}\exp\{-\lambda\tau_{1}\}\\&&-\frac{s^2lmr_{1}r_{2}A}{c\beta}\exp\{-\lambda\tau_{1}\}+sr_{1}r_{2}A\exp\{-\lambda\tau_{2}\}-sr_{1}r_{2}\exp\{-\lambda\tau_{2}\}\Big]=0.\end{eqnarray*}$

此时,取$\tau_{1}=0, \tau_{2}=0$,整理得

$\lambda^3+\lambda^2(r_{1}A+r_{2})+\lambda\bigg[r_{1}s(\frac{r_{2}}{s}A+\frac{mlr_{2}}{c\beta}A-\frac{mlr_{2}}{c\beta}+1-A)\bigg]+\bigg[sr_{1}r_{2}(\frac{sml}{c\beta})(A-1)\bigg]=0.$

令

$a_{1}=r_{1}A+r_{2}=r_{1}\frac{s+sml_{0}}{c\beta K-smlK}+r_{2}, $

$a_{2}=r_{1}s(\frac{r_{2}}{s}A+\frac{mlr_{2}}{c\beta}A-\frac{mlr_{2}}{c\beta}+1-A), $

$a_{3}=sr_{1}r_{2}(\frac{slm}{c\beta}-1)(A-1).$

根据Hurwitz判据,有

$a_{1}=r_{1}A+r_{2}=r_{1}\frac{s+sml_{0}}{c\beta K-amlK}+r_{2}>0, $

满足条件(A4);

$ a_{3}=sr_{1}r_{2}(\frac{slm}{c\beta})(A-1)=sr_{1}r_{2}(\frac{slm}{c\beta}-1)(\frac{s+sml_{0}}{c\beta K-smlK}-1)>0, $

满足条件(A5);

$\begin{eqnarray*}a_{1}a_{2}-a_{3}&=&(r_{1}\frac{s+sml_{0}}{c\beta K-smlK}+r_{2})\bigg[r_{1}s(\frac{r_{2}}{s}A+\frac{mlr_{2}}{c\beta}A-\frac{mlr_{2}}{c\beta}+1-A)\bigg]\\&&-\bigg[sr_{1}r_{2}(\frac{sml}{c\beta}-1)(A-1)\bigg]>0, \end{eqnarray*}$

满足条件(A6).

由此可知在$\tau_{1}=0, \tau_{2}=0$的情况下,如果满足条件(A4)-(A6),平衡点$E_{6}$是局部渐近稳定的.

从生物学上看, $E_{4}(x^*_{1}, 0, y^*_{1})$的不稳定性说明只有猎物和捕食者的系统不能稳定,而$E_{5}(K, l_{0}+lK, 0)$的稳定性说明只有猎物和共生者的系统具有稳定的可能性.

下面对系统(3.1)所做的平衡点稳定性分析进行数值模拟,对于情况较为复杂的平衡点进行数值分析.

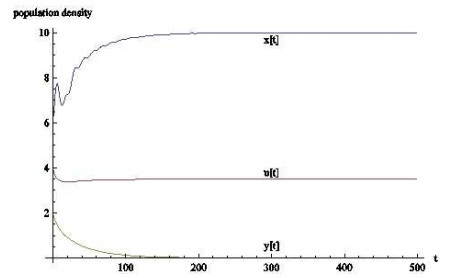
(1)  平衡点$E_{5}(K, l_{0}+lK, 0)$.

若条件(A3)成立,则平衡点$E_{5}(K, l_{0}+lK, 0)$是局部渐近稳定的,取参数$r_{1}=0.5, $$K=10;\beta=0.08, r_{2}=0.2, l_{0}=3, l=0.05, s=0.08, c=0.05, \tau_{1}=3, \tau_{2}=20, m=0.03, $$ e=2.7183, x(0)=6, u(0)=4, y(0)=2$.此时相应的平衡点$E_{5}(K, l_{0}+lK, 0)$为$(10, 3.5, 0), $满足条件(A3),从图 1可以看出系统最终稳定在(10, 3.5, 0).

生物学上看,当瓢虫和棉蚜的时滞忽略不计时,棉蚜和蚂蚁可以共存并最终保持稳定,而瓢虫的数量会一直减少,甚至会消失.

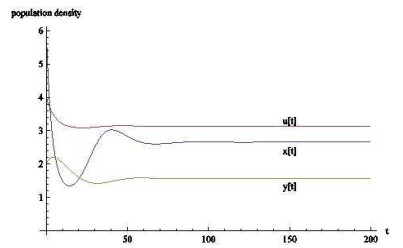
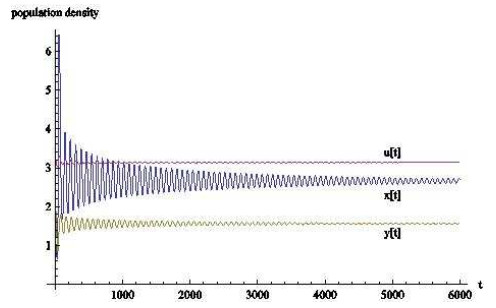
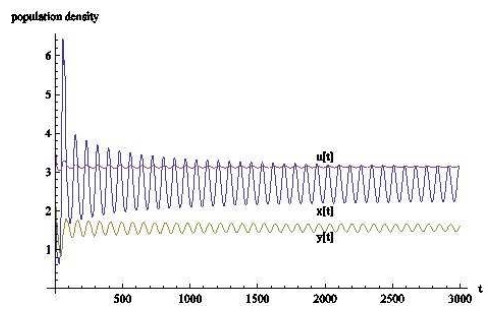
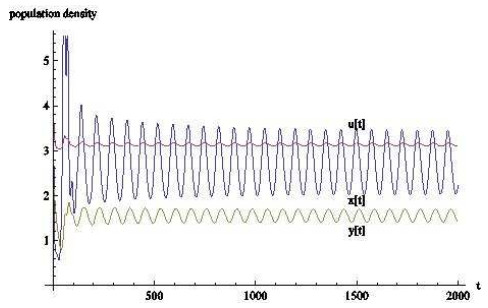
(2)  平衡点$E_{6}$.

对于正平衡点$E_{6}(x^*_{2}, u^*_{2}, y^*_{2})$,首先对其在没有时滞的情况下进行数值模拟,当$\tau_{1}=0, $$\tau_{2}=0$时,取参数值为: $r_{1}=0.5, $$ K=10, $$ \beta=0.25, $$ r_{2}=0.2, $$ l_{0}=3, l=0.05, $$ s=0.05, $$ c=0.08, $$ \tau_{1}=0, \tau_{2}=0, m=0.02, e=2.7183, x(0)=6, u(0)=4, y(0)=2$.此时的平衡点为$(2.67, 3.13, 1.56), $此时满足条件(A4)-(A6),从图 2可以看出系统最终稳定在$E_{6}(x^*_{2}, u^*{2}, y^*{2})=(2.67, 3.13, 1.56)$.

为了进一步探讨时滞对于种群动态的影响,我们令$\tau_{1}$固定,对$\tau_{2}$进行改变,然后令$\tau_{2}$固定,对$\tau_{1}$进行改变.由此,产生了不同的图像,见图 3-10 (此时的数据同图 2,只是时滞有所变化).

从图 3及图 4可以发现,当$\tau_{2}=0$时,存在$\tau_{01}>0$,使得$\tau_{1}<\tau_{01}$时,正平衡点$E_{6}$则仍具有稳定性；而当$\tau_{1}\geqslant\tau_{01}$时,正平衡点$E_{6}$将不再具有稳定性,方程呈周期性的波动变化.模拟结果表明, $8<\tau_{01}<9$.

从图 5及图 6可以发现,当$\tau_{1}=0$时,存在$\tau_{02}>0$,使得当$\tau_{1}<\tau_{02}$时,正平衡点$E_{6}$仍具有稳定性；当$\tau_{1}>\tau_{02}$时,正平衡点$E_{6}$将不再具有稳定性,方程呈周期性的波动变化.模拟结果表示, $22<\tau_{02}<23$.

在模拟过程中,发现当捕食者的时滞越高,平衡点由局部渐近稳定变为周期变化,食饵的时滞越低,反之亦然.从图 7及图 8可以看出$\tau_{2}=22$时, $\tau_{01}$在4到5之间,要小于8.从图 9及图 10可以看出$\tau_{1}=4$时, $\tau_{02}$在21到22之间,要小于22.

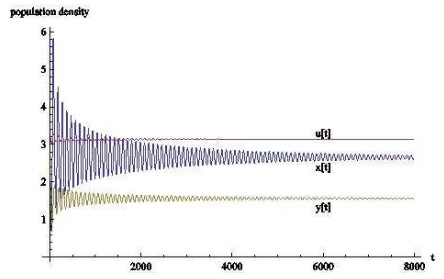
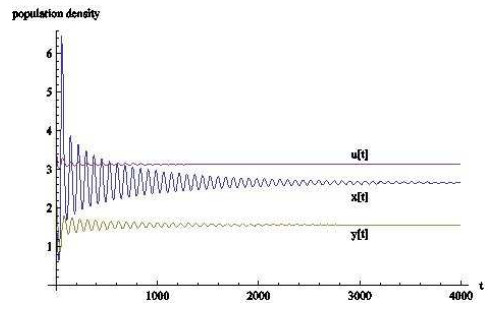
从数值模拟的结果来看,时滞对于基于瓢虫,棉蚜和蚂蚁的捕食者-猎物-共生者系统有相当大的影响.当时滞的作用忽略不计时,三种群最终会稳定在一个固定数值上；$\tau_{1}$为0时, $\tau_{2}$会有临界值$\tau_{02}$,使得当$\tau_{2}$超过临界值时,系统会由稳定变为周期性波动,反之亦然.当$\tau_{1}$和$\tau_{2}$不为0时,固定$\tau_{1}$,改变$\tau_{2}$的数值,同样会发生稳定性的改变,同时也会发现此时$\tau_{2}$的临界值$\tau_{02}$要低于$\tau_{1}$为0时的$\tau_{02}$,反之亦然,也就是说随着时滞的增大,系统由稳定变为周期性变化的时滞的临界值会降低^[12].

从生物学上看,当瓢虫和棉蚜的发育历期不断增长时,三者虽然会共存但数量会不停变化,可以这样认为,发育历期影响着自身种群的发展,并间接影响着其余种群的发展.

参见文献^[13-14],棉蚜从幼虫到若虫的时间约为4到6天,平均历期约为5天,瓢虫从幼虫到若虫的时间约为16到25天,常温时约为21天,取$\tau_{1}$为5, $\tau_{2}$为21,得到图 11,可以看出平常状态下,系统呈周期性变化.

对于本文所建立的捕食者-猎物-共生系统的模型,猎物和捕食者的时滞会对平衡点的稳定性起到重要作用,当时滞超过临界值时,数值模拟表明,系统会发生由稳定到周期波动的改变,说明捕食者和猎物的成长时间对系统会有相当重要的影响,从生物学上看,随着瓢虫和棉蚜的时滞的增长,即当发育历期的影响越来越大时,三者的关系会出现周期波动,这也更符合现实世界的情况.但由于棉蚜和瓢虫的发育历期会受温度、地域、气候等相关因素的影响,这里只采取了比较普遍的情况,所以可能在精确度上会有所影响.但同时结果表明,只有天敌可以部分抑制棉蚜的数量,但可能不足以控制害虫.如何有效控制害虫将是下一步要做的工作.

这对现实中的棉田有害生物的治理有所启发,判断棉蚜和瓢虫的发育历期,根据发育历期的长短预估将来发展的趋势,以此来设计相应的治理方案,如根据波动的情况来采取不同的治理方法,尤其要小心有剧烈波动时所产生的蚜虫大爆发的情况.

另外,基于文献[7-8],本文下一步的工作将对系统给出分支的理论判据,对数值模拟的结果给出理论上的证明.