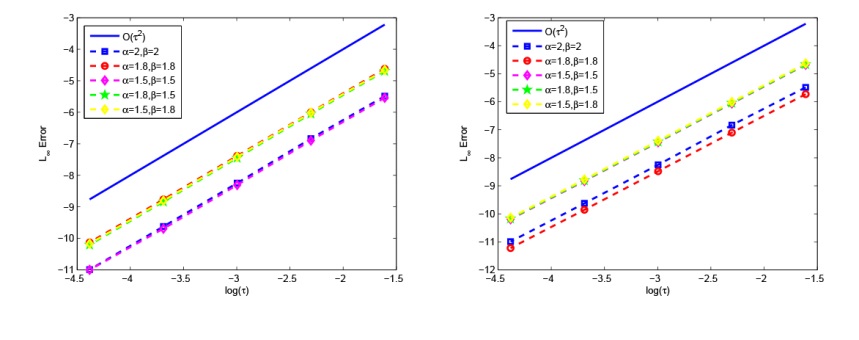
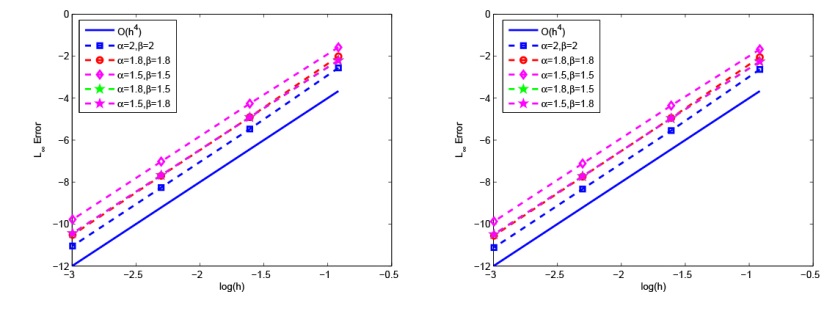
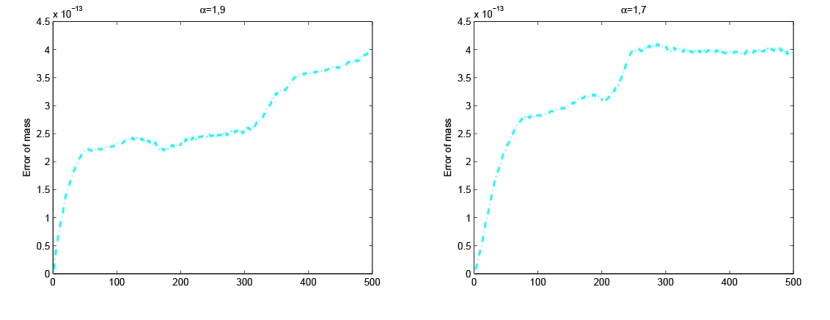
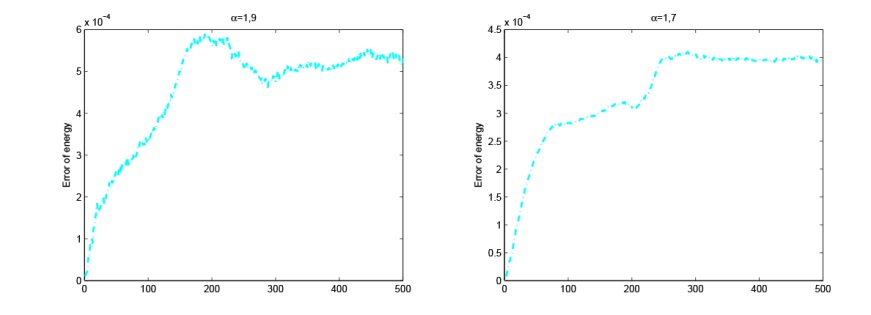
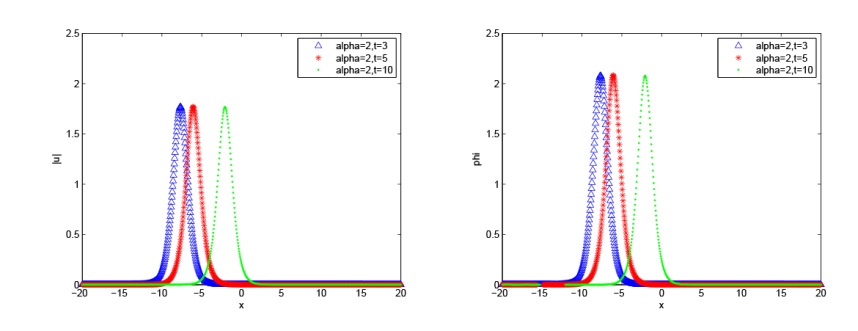
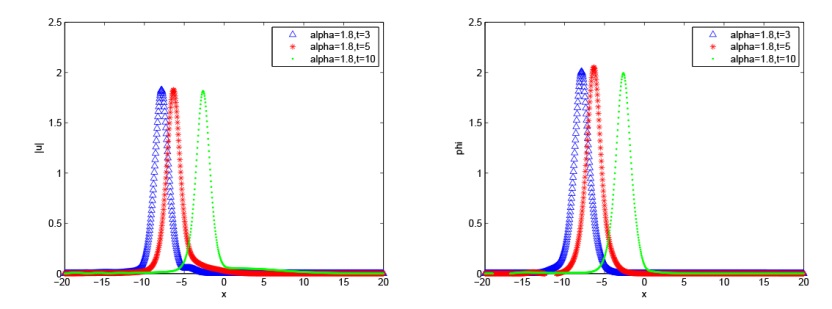
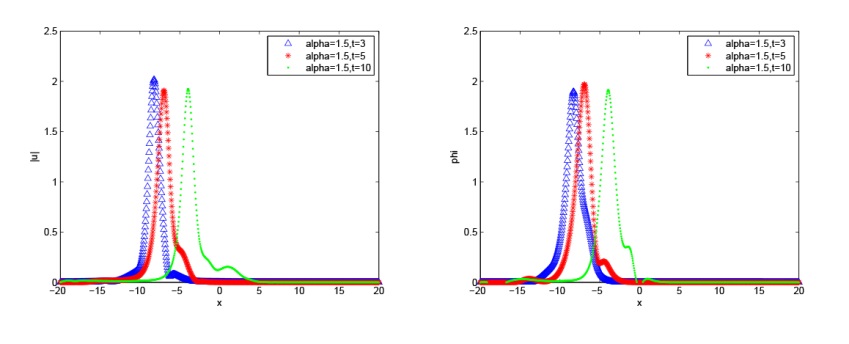
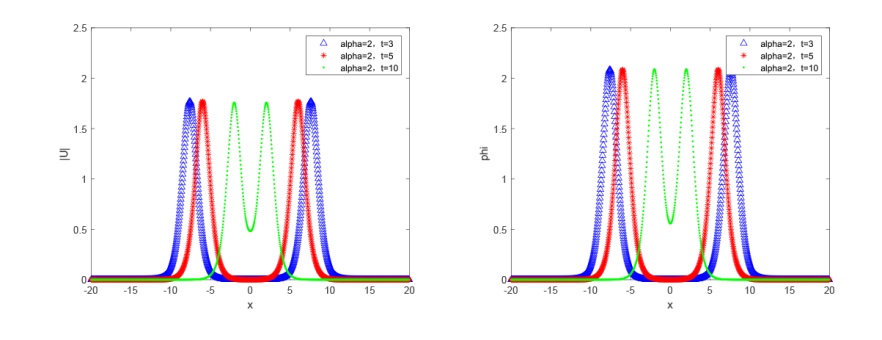
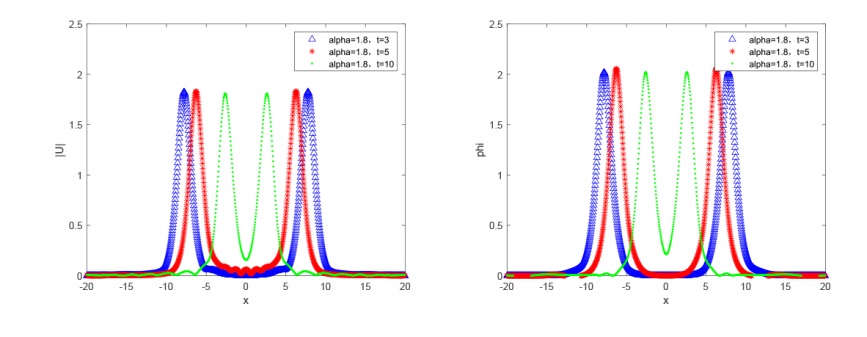
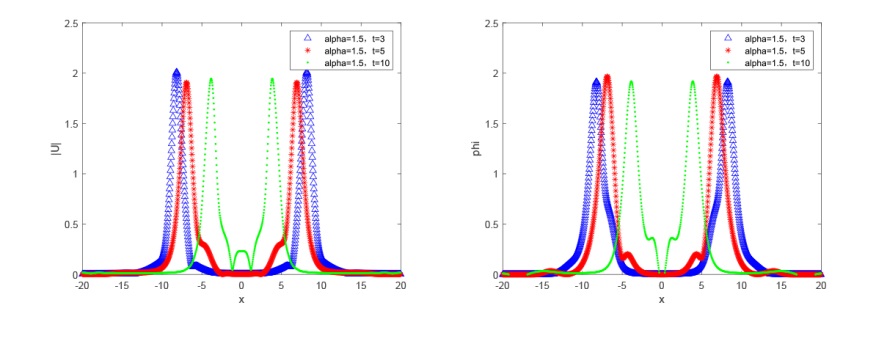
Acta mathematica scientia,Series A ›› 2024, Vol. 44 ›› Issue (5): 1319-1334.
Previous Articles Next Articles
Symplectic Difference Scheme for the Space Fractional KGS Equations
- School of Mathematics and Statistics, Pu'er University, Yunnan Pu'er 665000
-
Received:2022-11-07Revised:2024-03-26Online:2024-10-26Published:2024-10-16 -
Supported by:National Natural Science Foundation of China(12161070)
CLC Number:
- O242.2
Cite this article
Wang Junjie. Symplectic Difference Scheme for the Space Fractional KGS Equations[J].Acta mathematica scientia,Series A, 2024, 44(5): 1319-1334.
share this article
| [1] | Feng K, Qin M. Symplectic Geometric Algorithms for Hamiltonian Systems. Berlin: Springer, 2009 |
| [2] |
Channel P, Scovel C. Symplectic integration of Hamiltonian systems. Nonlinearity, 1990, 3: 231-259
doi: 10.1088/0951-7715/3/2/001 |
| [3] | Liu X, Qi Y, He J, Ding P. Recent progress in symplectic algorithms for use in quantum systems. Communications in Computational Physcis, 2007, 2(1): 1-53 |
| [4] | Mclachlan R. Symplectic integration of Hamiltonian wave equations. Numerische Mathematik, 1994, 66: 465-492 |
| [5] | Sanz-Serna J, Calvo M. Numerical Hamiltonian Problems. London: Chapman and Hall, 1994 |
| [6] | Hairer E, Lubich C, Wanner G. Geometric Numerical Integration: Structure Preserving Algorithms for Ordinary DifferentialEquations. Berlin: Springer-Verlag, 2002 |
| [7] | Bridges T, Reich S. Numerical methods for Hamiltonian PDEs. Journal of Physics A Mathematical and General, 2006, 39: 5287-5320 |
| [8] | Gong Y, Cai J, Wang Y. Some new structure-preserving algorithms for general multi-symplectic formulations of Hamiltonian PDEs. Journal of Computational Physics, 2014, 279: 80-102 |
| [9] | Bridges T. Multi-symplectic structures and wave propagation. Mathematical Proceedings of the Cambridge Philosophical Society, 1997, 121: 147-190 |
| [10] | Chen Y, Sun Y, Tang Y. Energy-preserving numerical methods for Landau-Lifshitz equation. Journal of Physics A Mathematical and Theoretical, 2011, 44(29): 295207 |
| [11] | Kong L, Hong J, Zang J. Splitting multi-symplectic integrators for Maxwell's equation. Journal of Computational Physics, 2010, 229: 4259-4278 |
| [12] | Reich S. Multi-symplectic Runge-Kutta collocation methods for Hamiltonian wave equations. Journal of Computational Physics, 2000, 157: 473-499 |
| [13] | Ober-Blöbaum S. Galerkin variational integrators and modified symplectic Runge-Kutta methods. IMA Journal of Numerical Analysis, 2017, 37: 375-406 |
| [14] | Mei L, Wu X. Symplectic exponential Runge-Kutta methods for solving nonlinear Hamiltonian systems. Journal of Computational Physics, 2017, 338: 567-584 |
| [15] | Wang P, Hong J, Xu D. Construction of symplectic Runge-Kutta methods for stochastic Hamiltonian systems. Computer Physics Communications, 2017, 21(1): 237-270 |
| [16] | Guo B, Pu X, Huang F. Fractional Partial Differential Equations and Their Numerical Solutions. Beijing: World Scientific Publishing, 2011 |
| [17] | Li C P, Zeng F H. Numerical Methods for Fractional Calculus. New York: CRC Press, 2015 |
| [18] | 孙志高, 高广花. 分数阶偏微分方程的有限差分方法. 北京: 科学出版社, 2015 |
| Sun Z G, Gao G H. Finite Difference Methods for Fractional-order Differential Equations. Beijing: Science Press, 2015 | |
| [19] | 刘发旺, 庄平辉, 刘青霞. 分数阶偏微分方程数值方法及其应用. 北京: 科学出版社, 2015 |
| Liu F W, Zhuang P H, Liu Q X. Numerical Methods and Their Applications of Fractional Partial Differential Equations. Beijing: Science Press, 2015 | |
| [20] | Wang P, Huang C, Zhao L. Point-wise error estimate of a conservative difference scheme for the fractional Schrödinger equation. Journal of Computational and Applied Mathematics, 2016, 306: 231-247 |
| [21] | Wang D, Xiao A, Yang W. Crank-Nicolson difference scheme for the coupled nonlinear Schrödinger equations with the Riesz space fractional derivative. Journal of Computational Physics, 2013, 242: 670-681 |
| [22] | Zhao X, Sun Z, Hao Z. A fourth-order compact ADI scheme for two-dimensional nonlinear space fractional Schrödinger equation. SIAM Journal on Scientific Computing, 2014, 36(6): A2865-A2886 |
| [23] | Bueno-Orovio A, Kay D, Burrage K. Fourier spectral methods for fractional-in-space reaction-diffusion equations. BIT Numerical Mathematics, 2014, 54(4): 937-954 |
| [24] | Pindza E, Owolabi K. Fourier spectral method for higher order space fractional reaction-diffusion equations. Commun Nonlinear Sci Numer Simulat, 2016, 40: 112-128 |
| [25] | Wang J. High-order conservative schemes for the space fractional nonlinear Schrödinger equation. Applied Numerical Mathematics, 2021, 165: 248-269 |
| [26] | Gao G, Sun Z. A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. Journal of Computional Physics, 2014, 259: 33-50 |
| [27] | Alikhanov A. A new difference for the time fractional diffusion equation. J Comput Phys, 2015, 280: 424-438 |
| [28] | Jiang S, Zhang J, Zhang Q, Zhang Z. Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations. Communications in Computational Physics, 2017, 21(3): 650-678 |
| [29] | Stynes M, O'Riordan E, Gracia J L. Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM Journal on Numerical Analysis, 2017, 55: 1057-1079 |
| [30] | Jin B, Lazarov R, Pasciak J, Zhou Z. Error analysis of semidiscrete finite element methods for inhomogeneous time-fractional diffusion. IMA Journal of Numerical Analysis, 2015, 35(2): 561-582 |
| [31] | Jin B, Lazarov R, Zhou Z. Two fully discrete schemes for fractional diffusion and diffusion-wave equations with nonsmooth data. SIAM Journal on Scientific Computing, 2016, 38(1): A146-A170 |
| [32] | Yang Y, Chen Y, Huang Y, Wei H. Spectral collocation method for the time-fractional diffusion-wave equation and convergence analysis. Computational & Applied Mathematics, 2017, 73: 1218-1232 |
| [33] | Xiao A, Wang J. Symplectic scheme for the Schrödinger equation with fractional Laplacian. Applied Numerical Mathematics, 2019, 146: 469-487 |
| [34] | Wang J. Symplectic-preserving Fourier spectral scheme for space fractional Klein-Gordon-Schrödinger equations. Numerical Methods for Partial Differential Equations, 2021, 37: 1030-1056 |
| [35] | Wang P, Huang C. Structure-preserving numerical methods for the fractional Schrödinger equation. Applied Numerical Mathematics, 2018, 129: 137-158 |
| [36] | Celik C. Duman M. Crank-Nicolson method for the fractional diffusion equation with the Riesz fractional derivative. Journal of Computational Physics, 2012, 231: 1743-1750 |
| [1] | Yu Ting, Dong Ying. The Convergence Rate of the Fast Signal Diffusion Limit for a Three-Dimensional Keller-Segel-Stokes System [J]. Acta mathematica scientia,Series A, 2024, 44(4): 925-945. |
| [2] | Ma Xiaojun, Chen Fu, Jia Zhifu. Research on a Strong Convergence Theorem for Proximal Split Feasibility Problems with Non-Lipschitz Stepsizes [J]. Acta mathematica scientia,Series A, 2024, 44(4): 1052-1065. |
| [3] | Jian Jinbao, Dai Yu, Yin Jianghua. An Inertial Conjugate Gradient Projection Method for the Split Feasibility Problem [J]. Acta mathematica scientia,Series A, 2024, 44(4): 1066-1079. |
| [4] | Nie Jialin, Long Xianjun. A Golden Ratio Primal-Dual Algorithm for a Class of Nonsmooth Saddle Point Problems [J]. Acta mathematica scientia,Series A, 2024, 44(4): 1080-1091. |
| [5] | Zhang Xiao, Zhang Hongwu. Fractional Tikhonov Regularization Method for an Inverse Boundary Value Problem of the Fractional Elliptic Equation [J]. Acta mathematica scientia,Series A, 2024, 44(4): 978-993. |
| [6] |
Zhang Jie, Sun Yiming, Liu Yongping.
EC-tractability of Multivariate  |
| [7] | Liu Hua, Basma Al-Shutnawi. On Convergence Sets of Power Series with Holomorphic Coefficients [J]. Acta mathematica scientia,Series A, 2024, 44(3): 563-574. |
| [8] | Wang Weimin, Yan Wei. Convergence Problem and Dispersive Blow-up for the Modified Kawahara Equation [J]. Acta mathematica scientia,Series A, 2024, 44(3): 595-608. |
| [9] | Liu Jinghua, Li Lin. Homeomorphic Solutions of Iterative Functional Equations [J]. Acta mathematica scientia,Series A, 2024, 44(2): 313-325. |
| [10] | Cai Yu, Zhou Guanghui. Global Convergence of a WYL Type Spectral Conjugate Gradient Method [J]. Acta mathematica scientia,Series A, 2024, 44(1): 173-184. |
| [11] | Chen Jianhua, Peng Jianwen. Research on the Convergence Rate of Bregman ADMM for Nonconvex Multiblock Optimization [J]. Acta mathematica scientia,Series A, 2024, 44(1): 195-208. |
| [12] |
Zhang Jie,Zhao Donghai.
On Second Order Complex Differential Equations with Coefficients of Period    |
| [13] | Jian Jinbao,Lin Hui,Ma Guodong. A Splitting Sequence Quadratic Programming Algorithm for the Large-Scale Nonconvex Nonseparable Optimization Problems [J]. Acta mathematica scientia,Series A, 2023, 43(4): 1284-1296. |
| [14] | Wang Yang,Li Jian,Li Yi,Qin Yi. Analysis of a New Time Filter Algorithm for the Unsteady Stokes/Darcy Model [J]. Acta mathematica scientia,Series A, 2023, 43(3): 829-854. |
| [15] | Yu Yikang,Niu Jing. A Kind of Numerical Algorithm for Elliptic Interface Problem [J]. Acta mathematica scientia,Series A, 2023, 43(3): 883-895. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 176
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 54
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|