Acta mathematica scientia,Series A ›› 2024, Vol. 44 ›› Issue (5): 1242-1282.
Previous Articles Next Articles
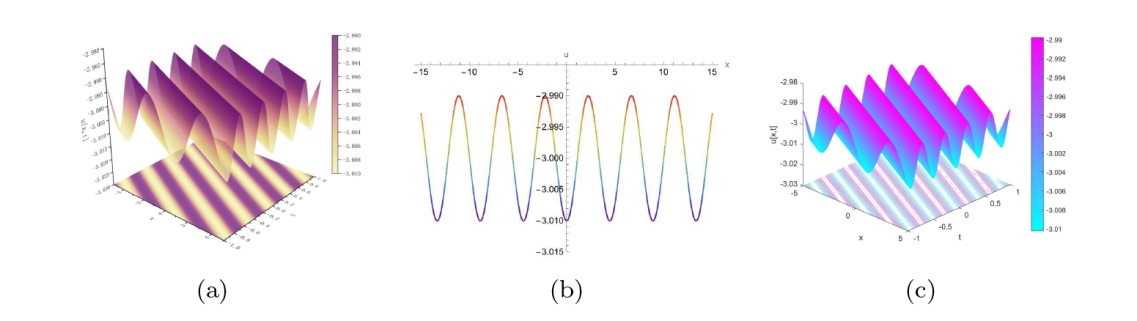
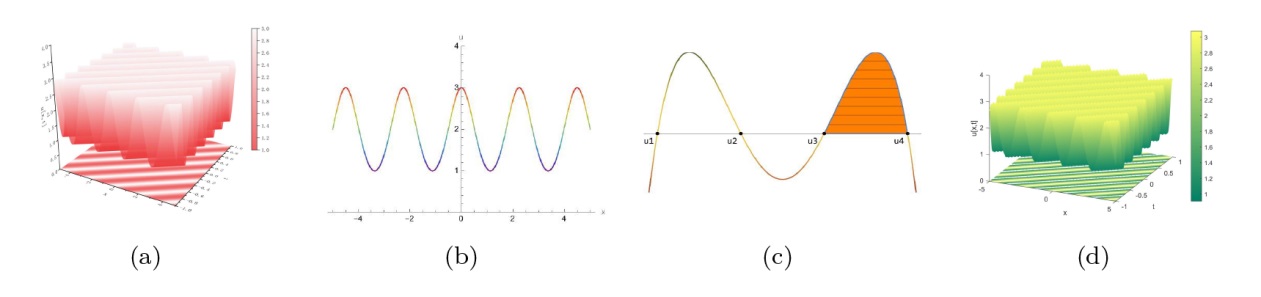
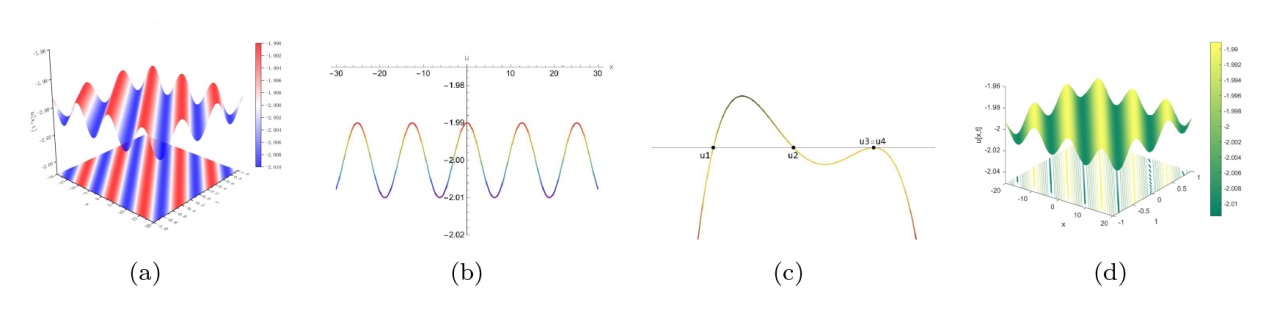
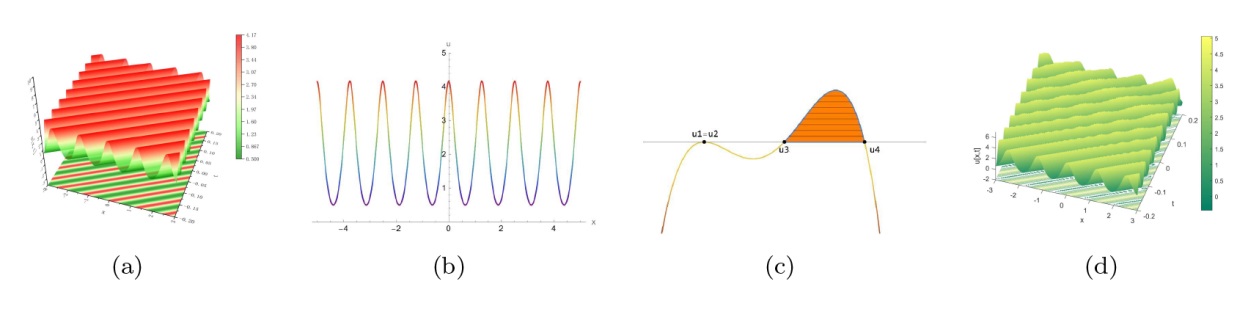
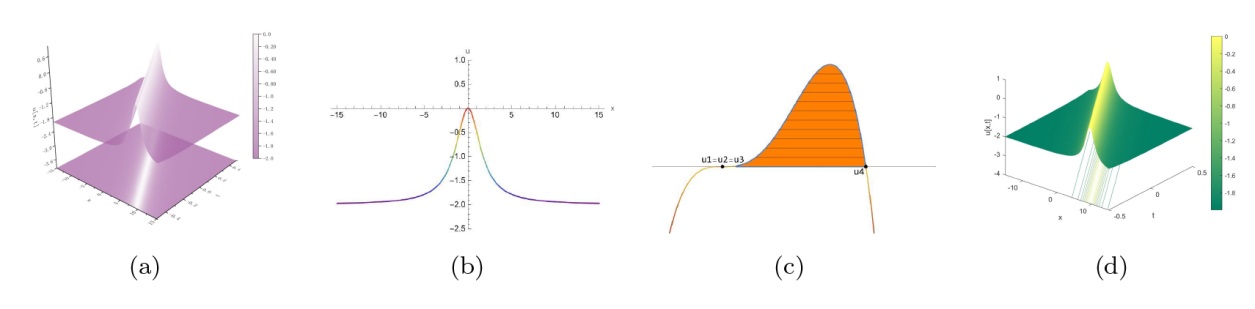
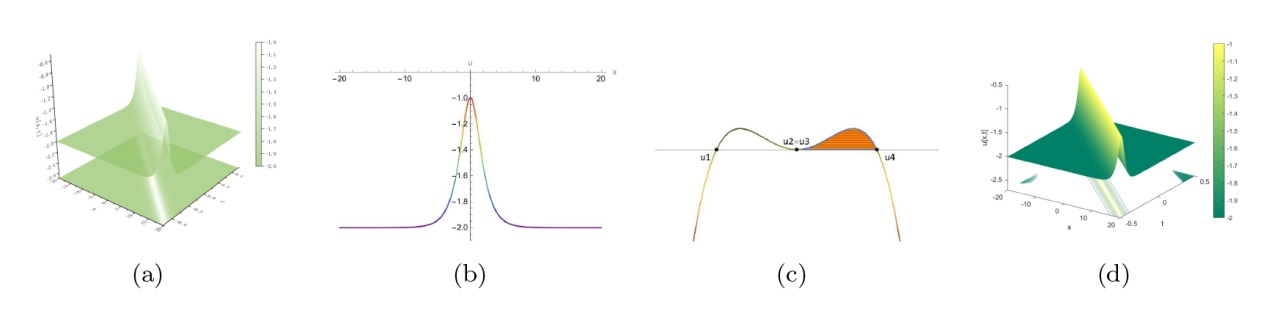
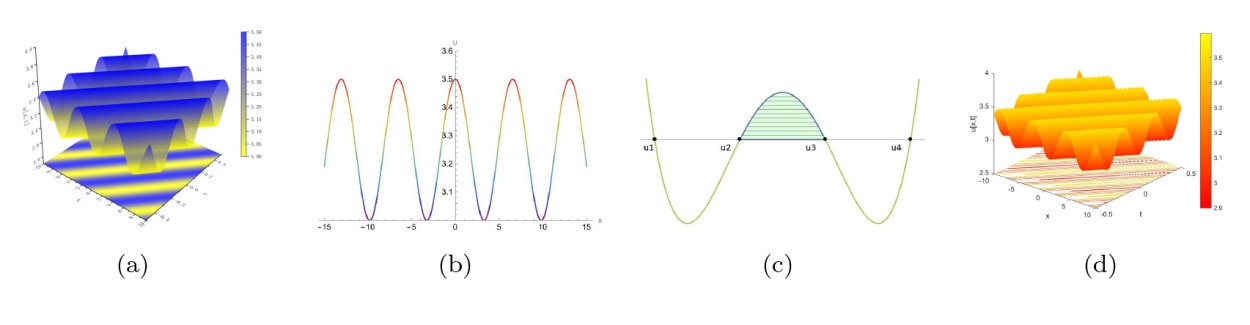
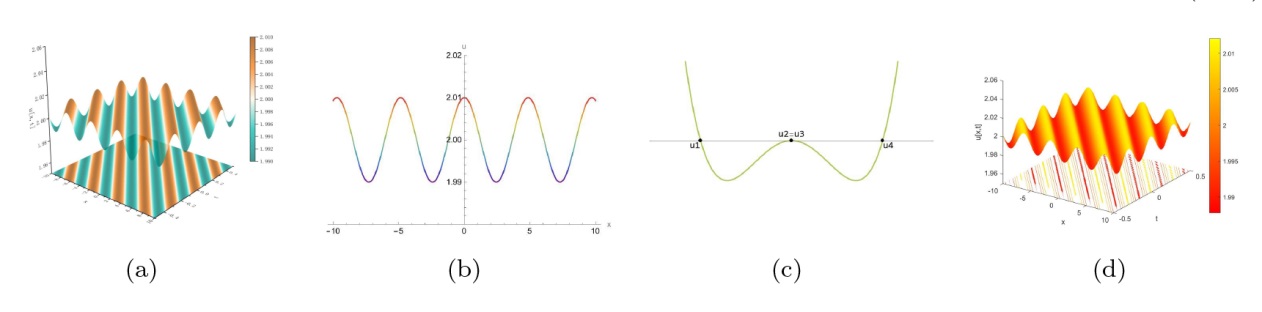
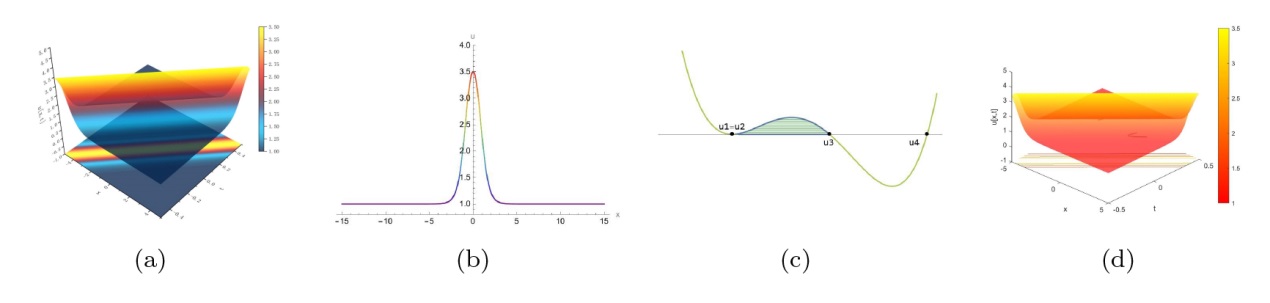
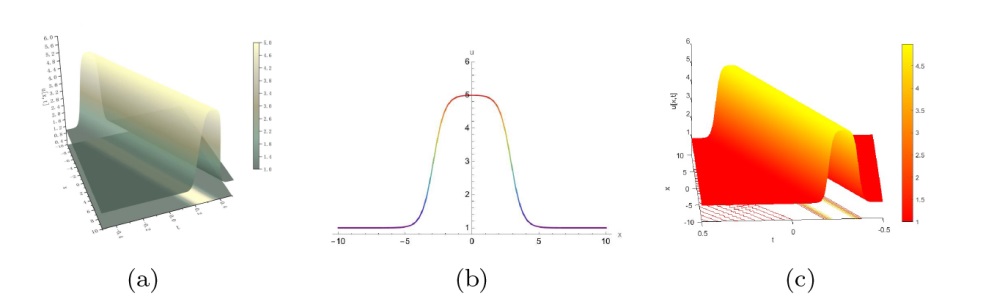
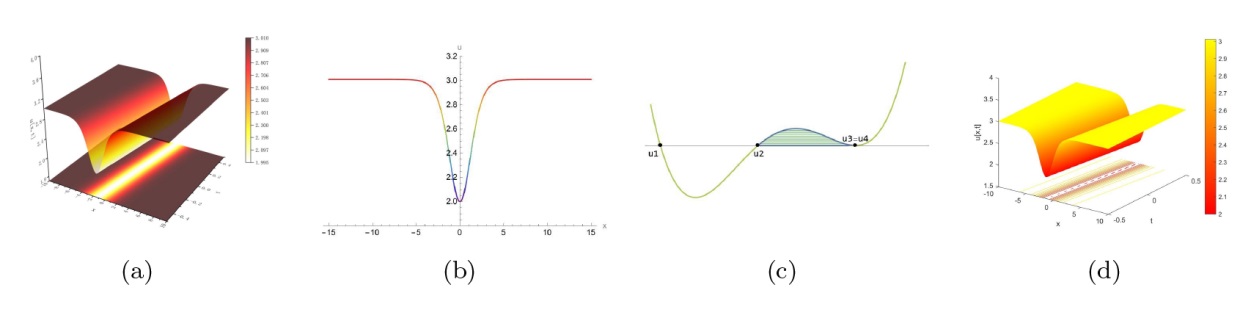
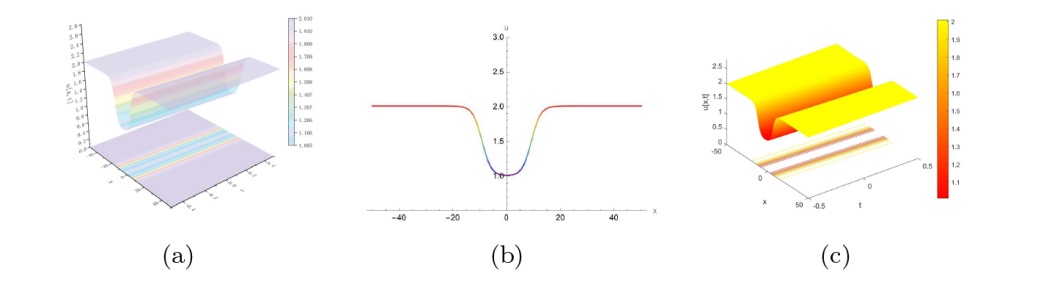
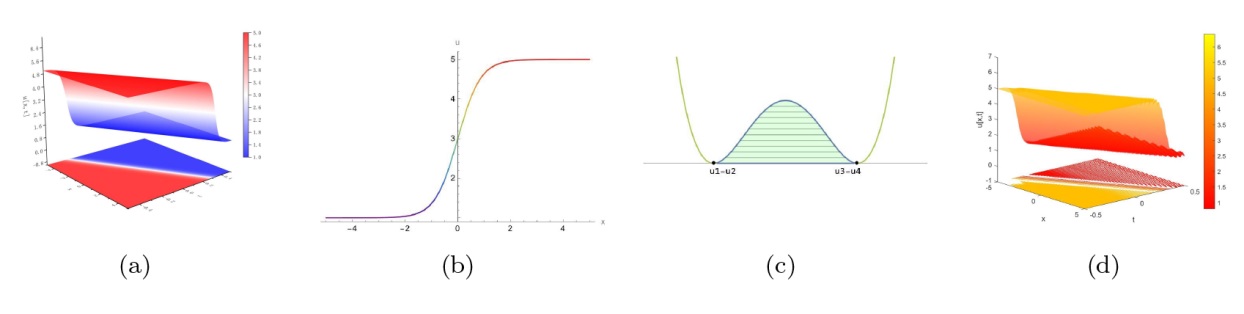
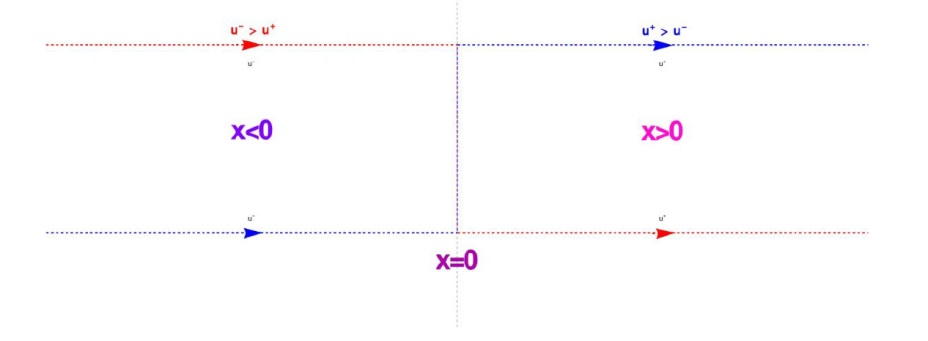
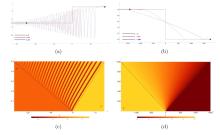
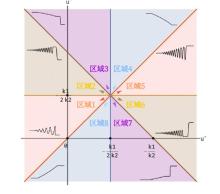
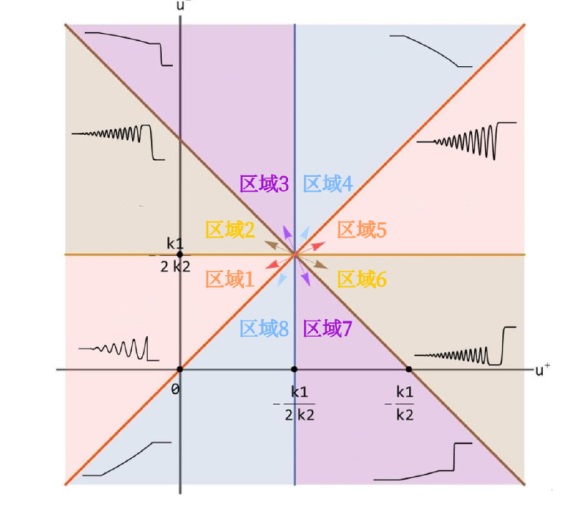
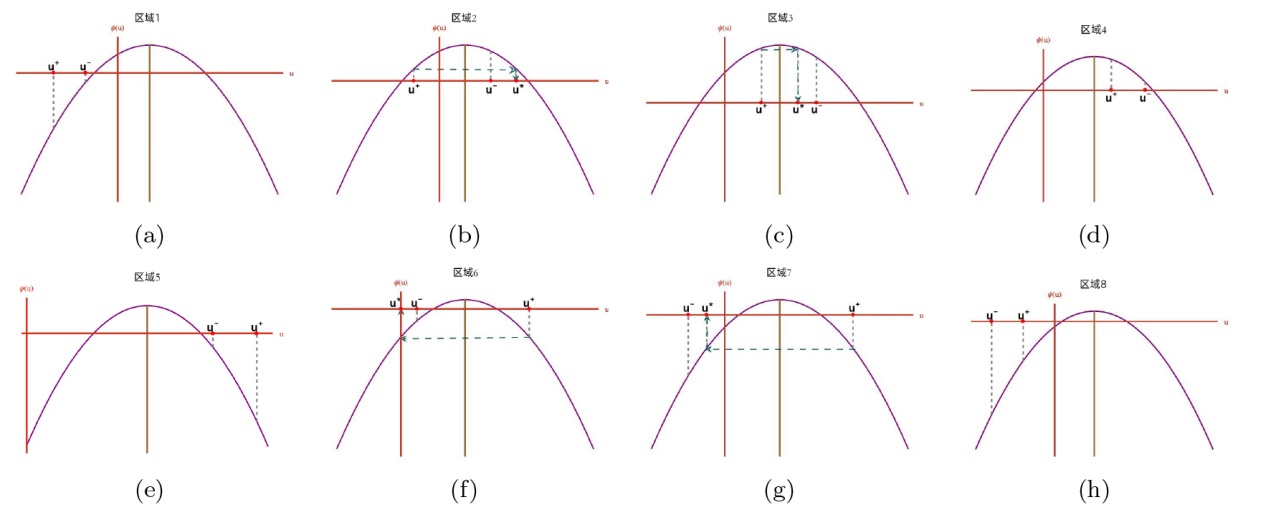
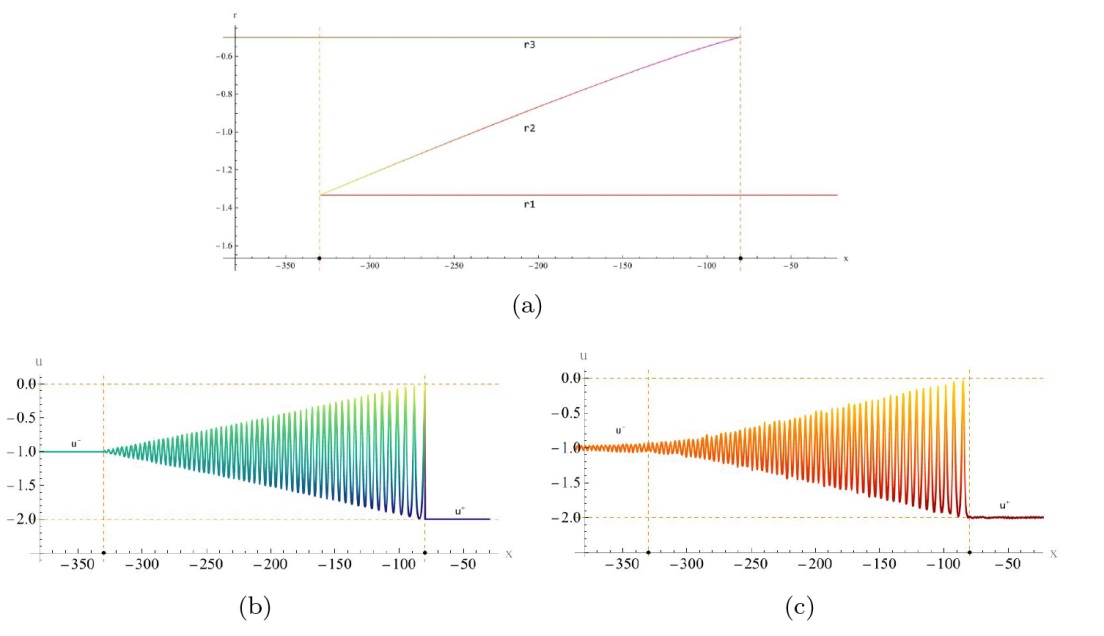
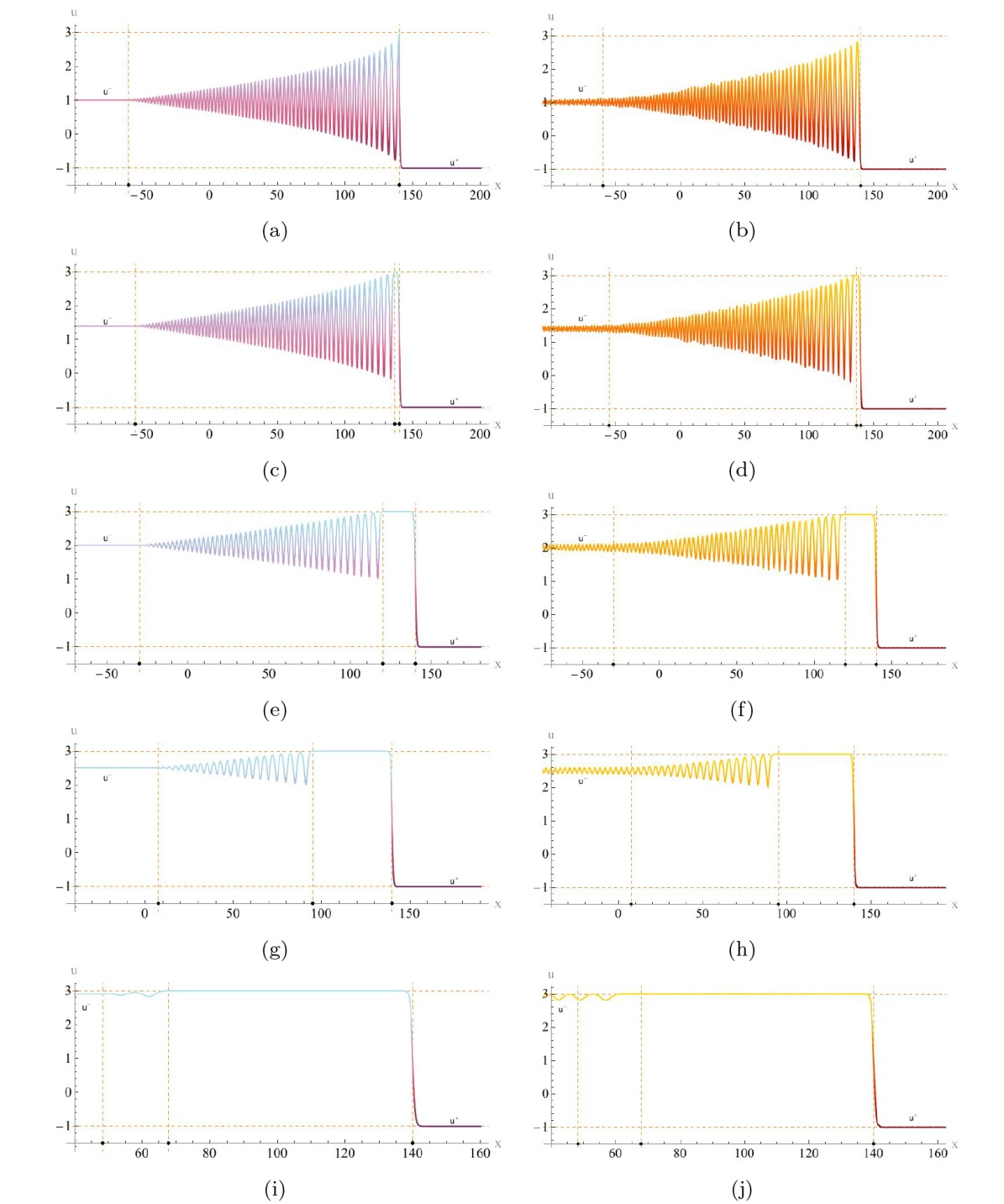
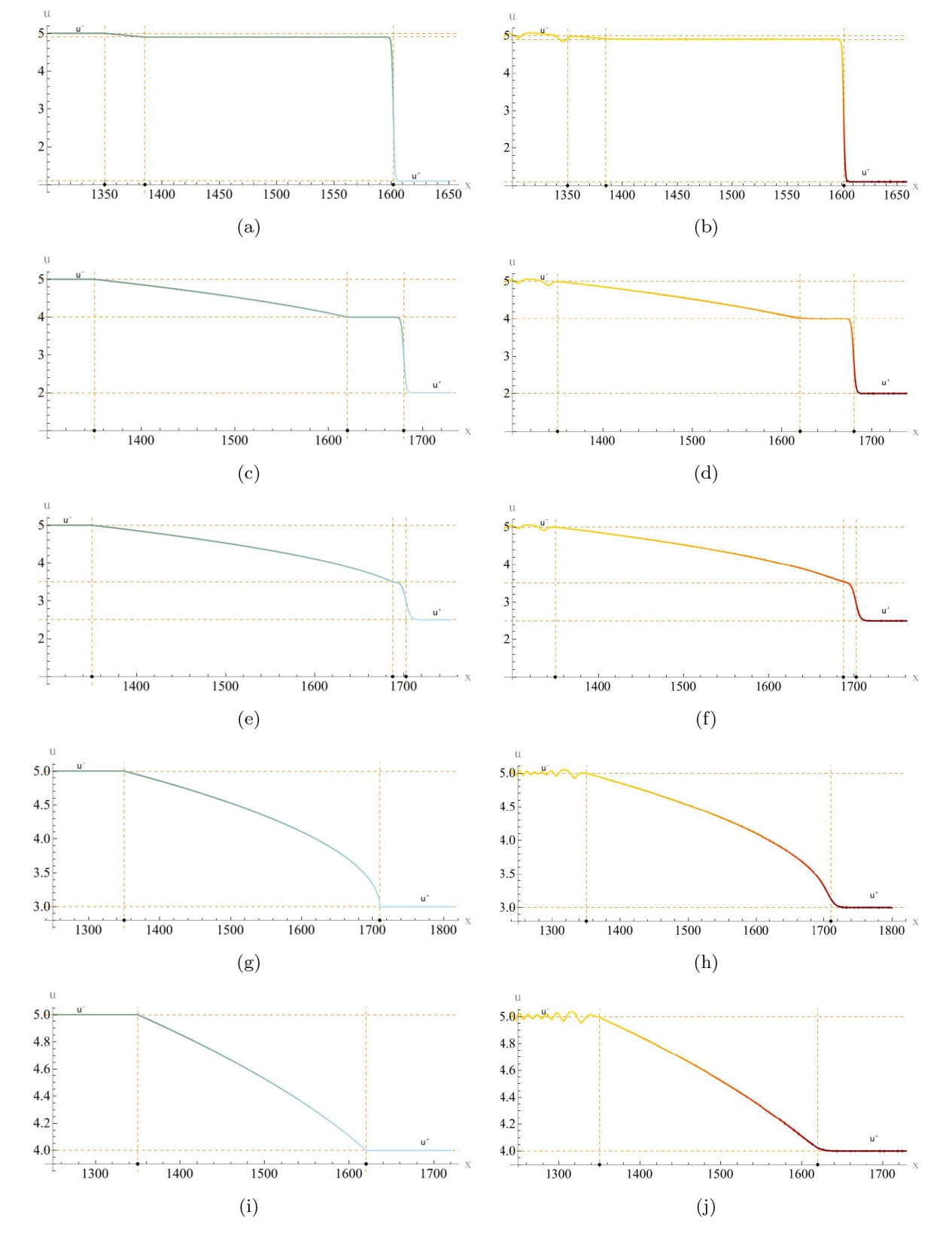
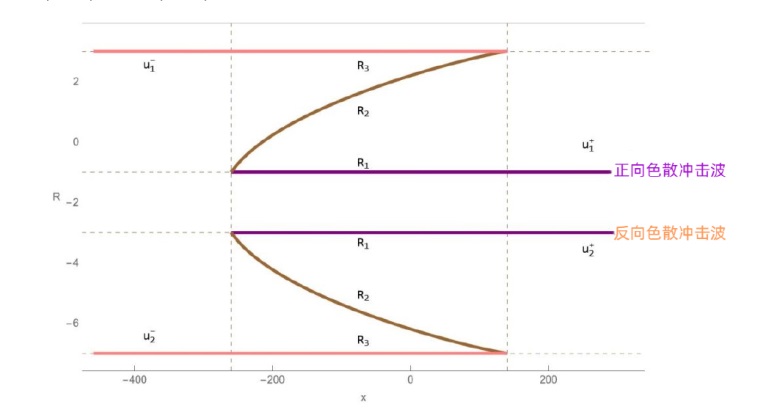
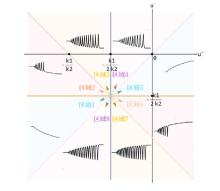
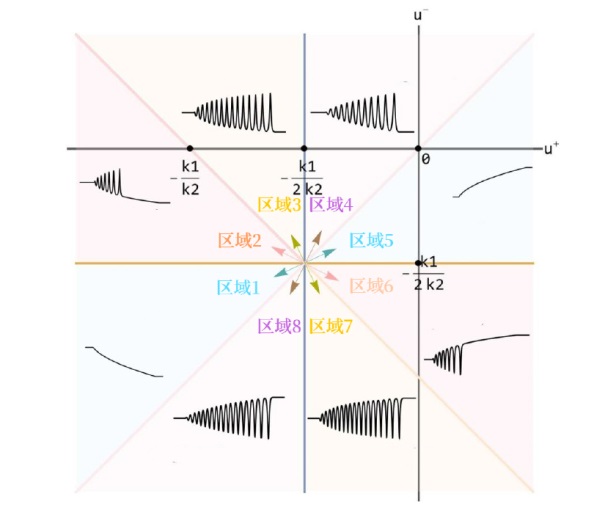
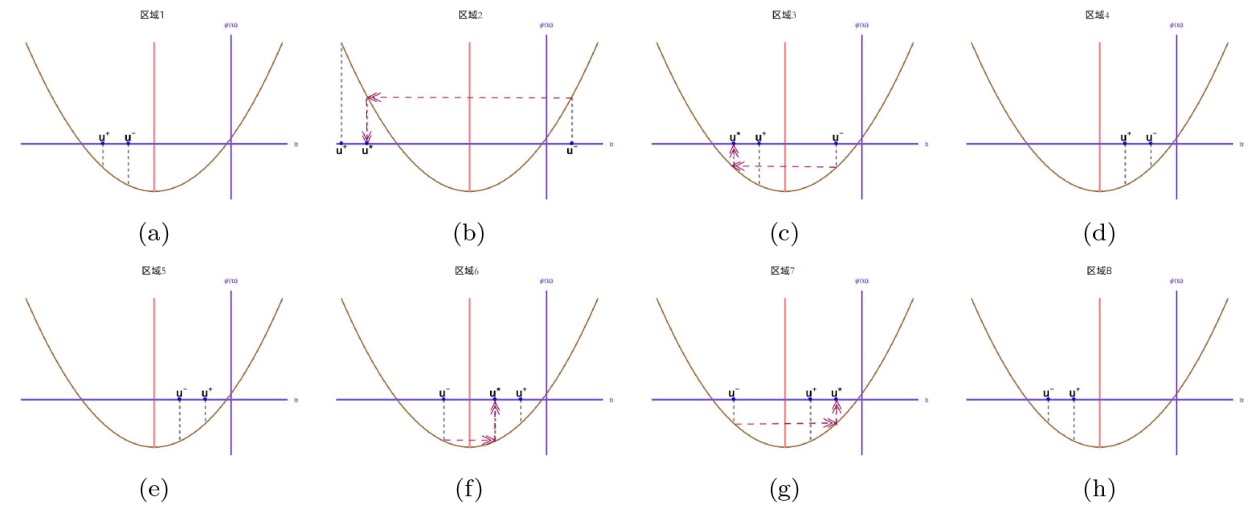
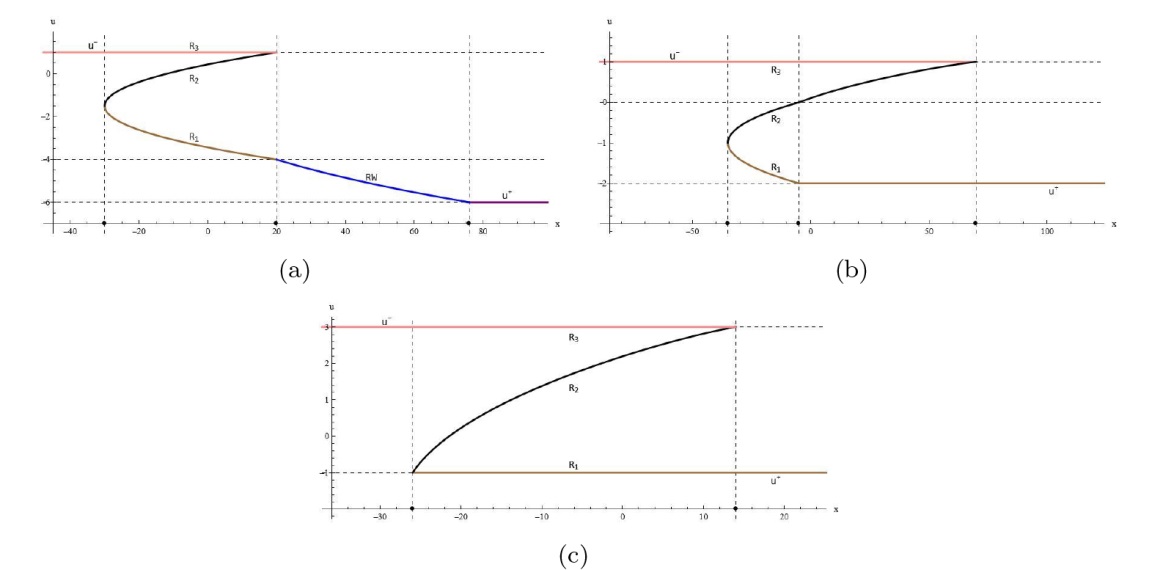
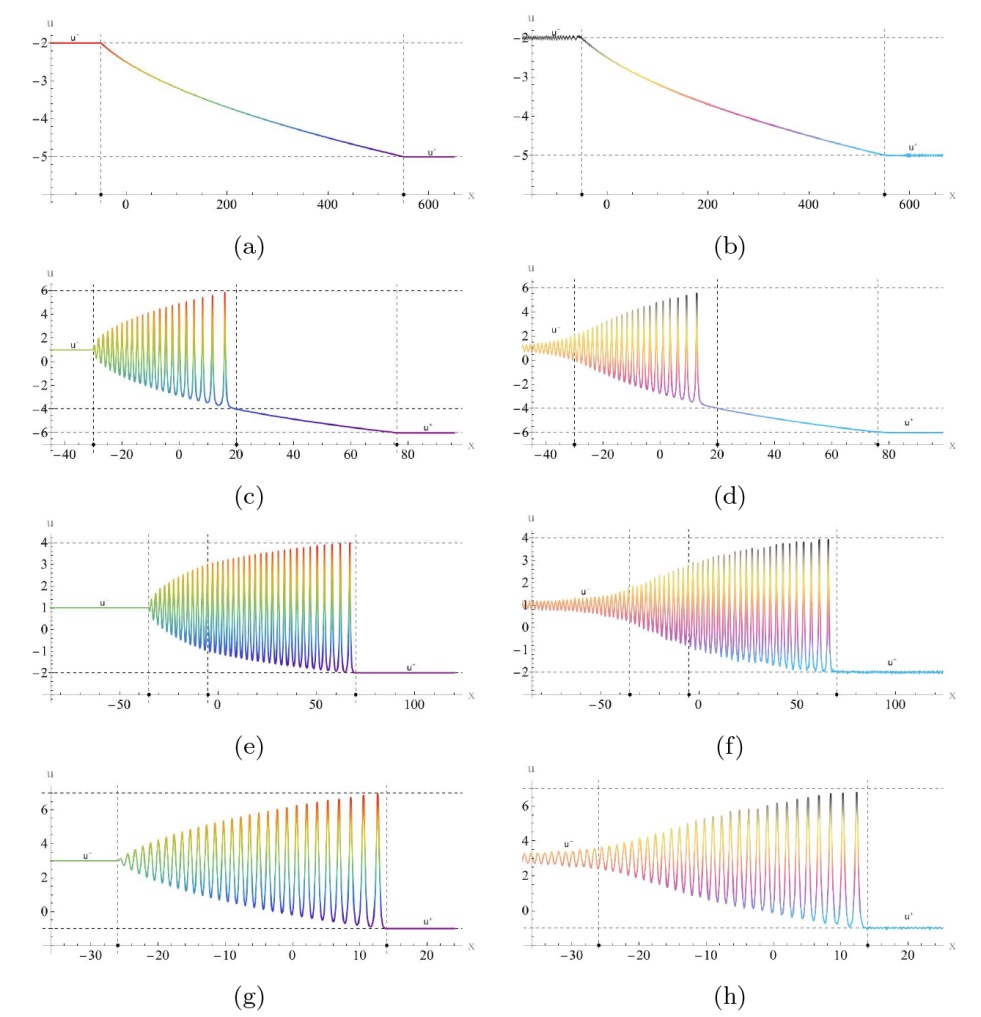
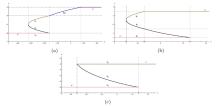
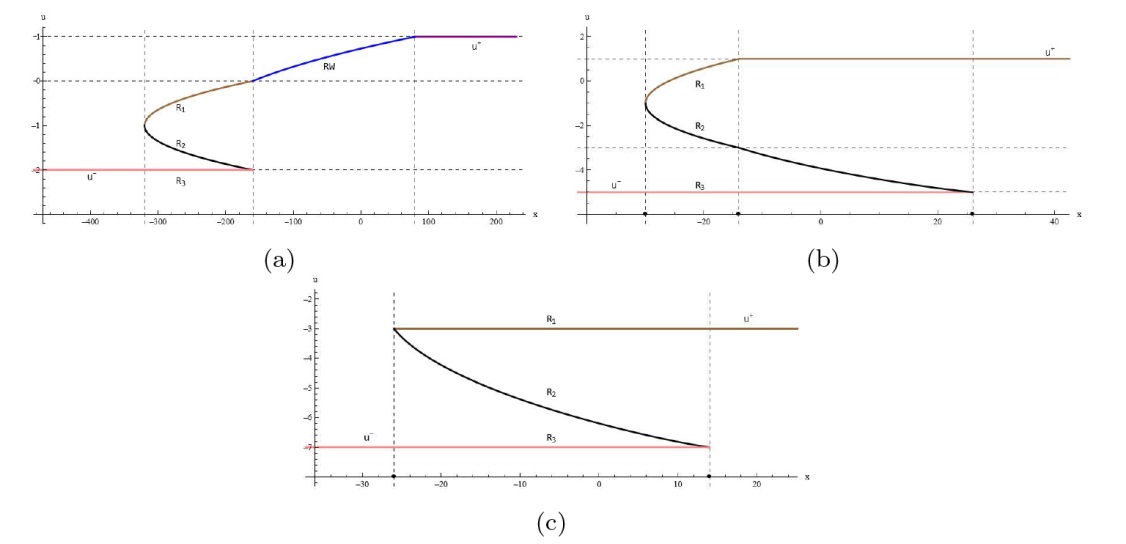
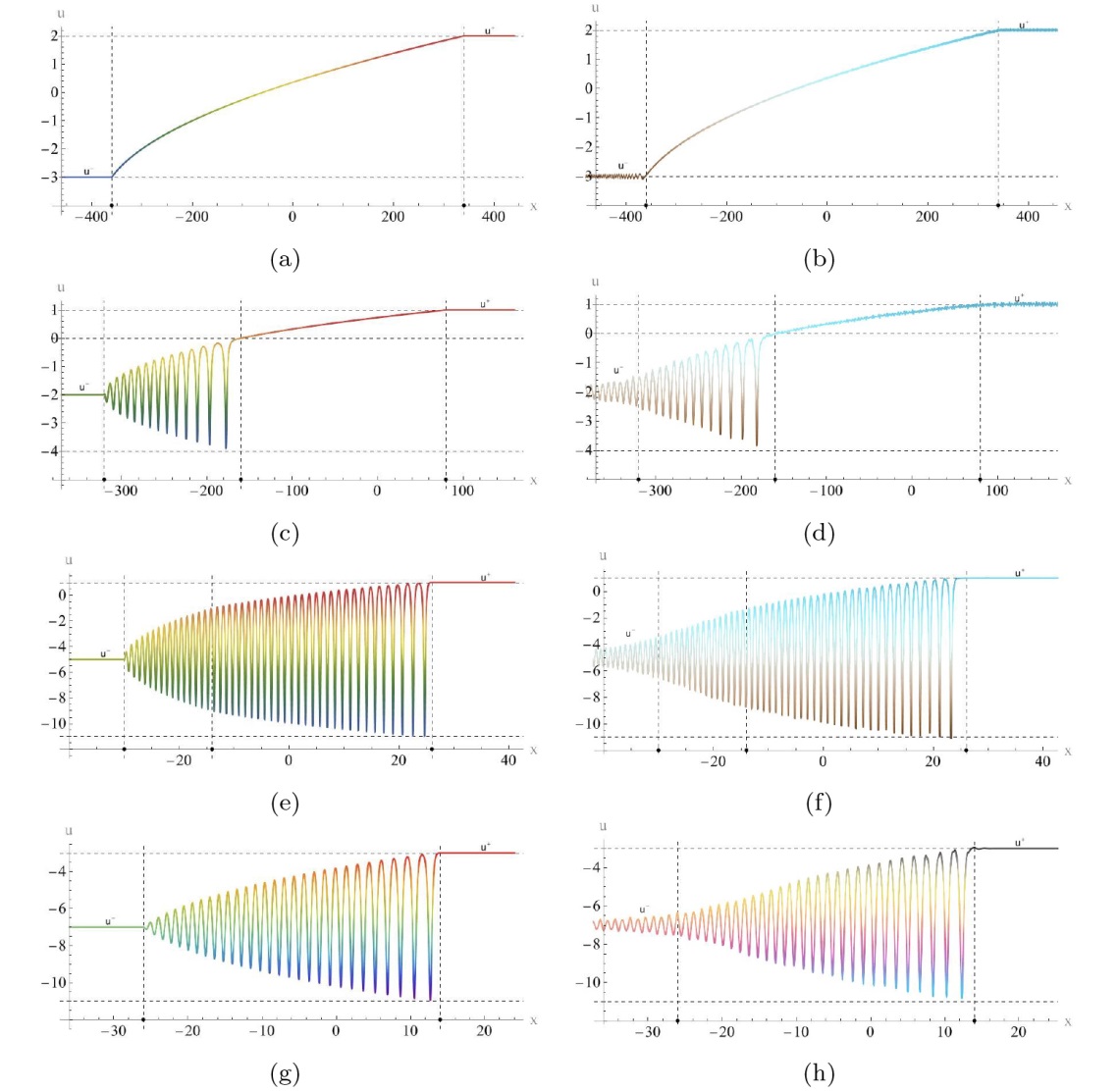
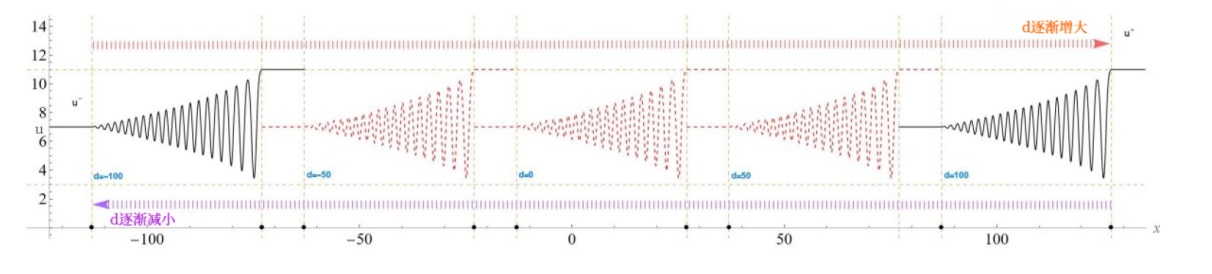
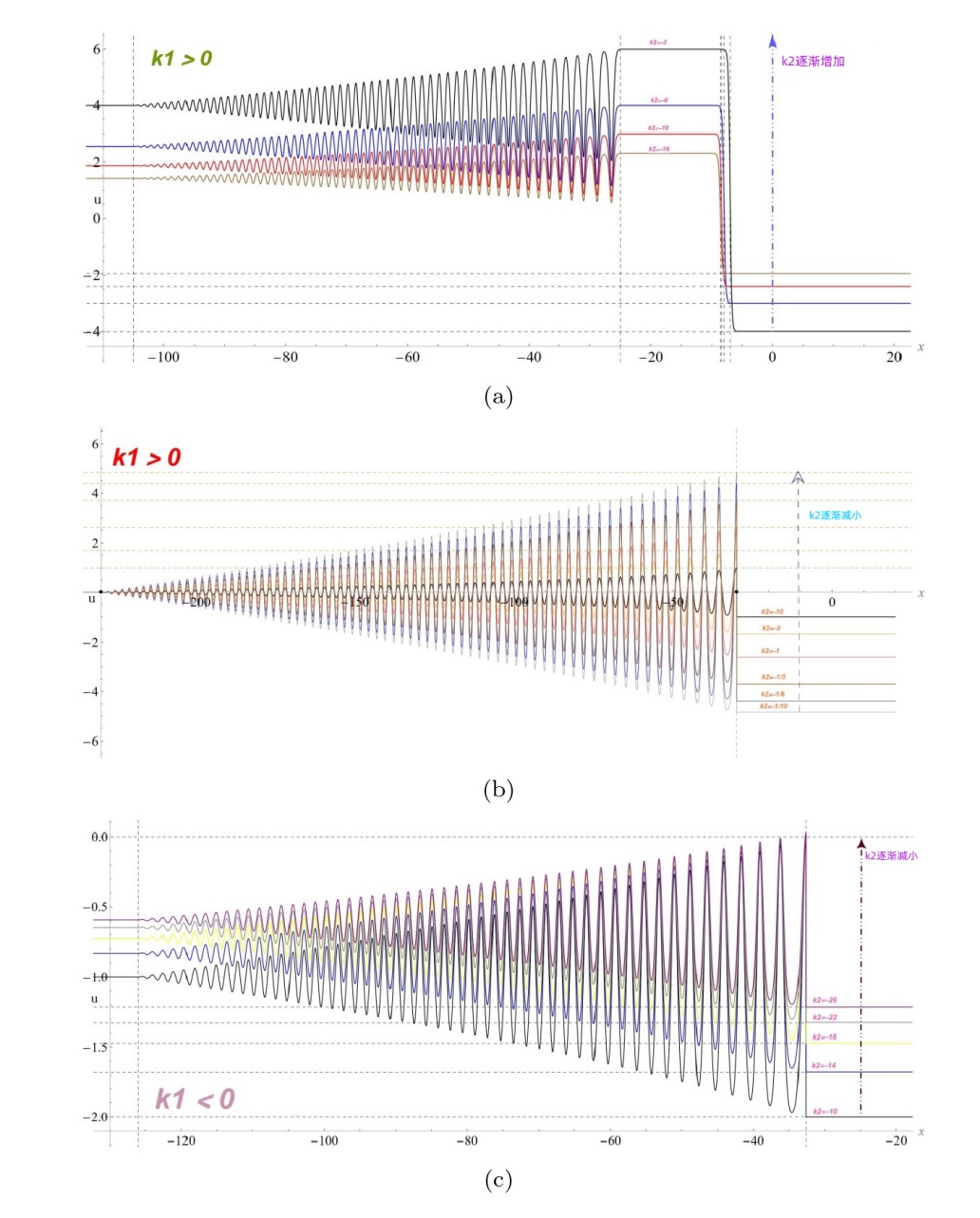
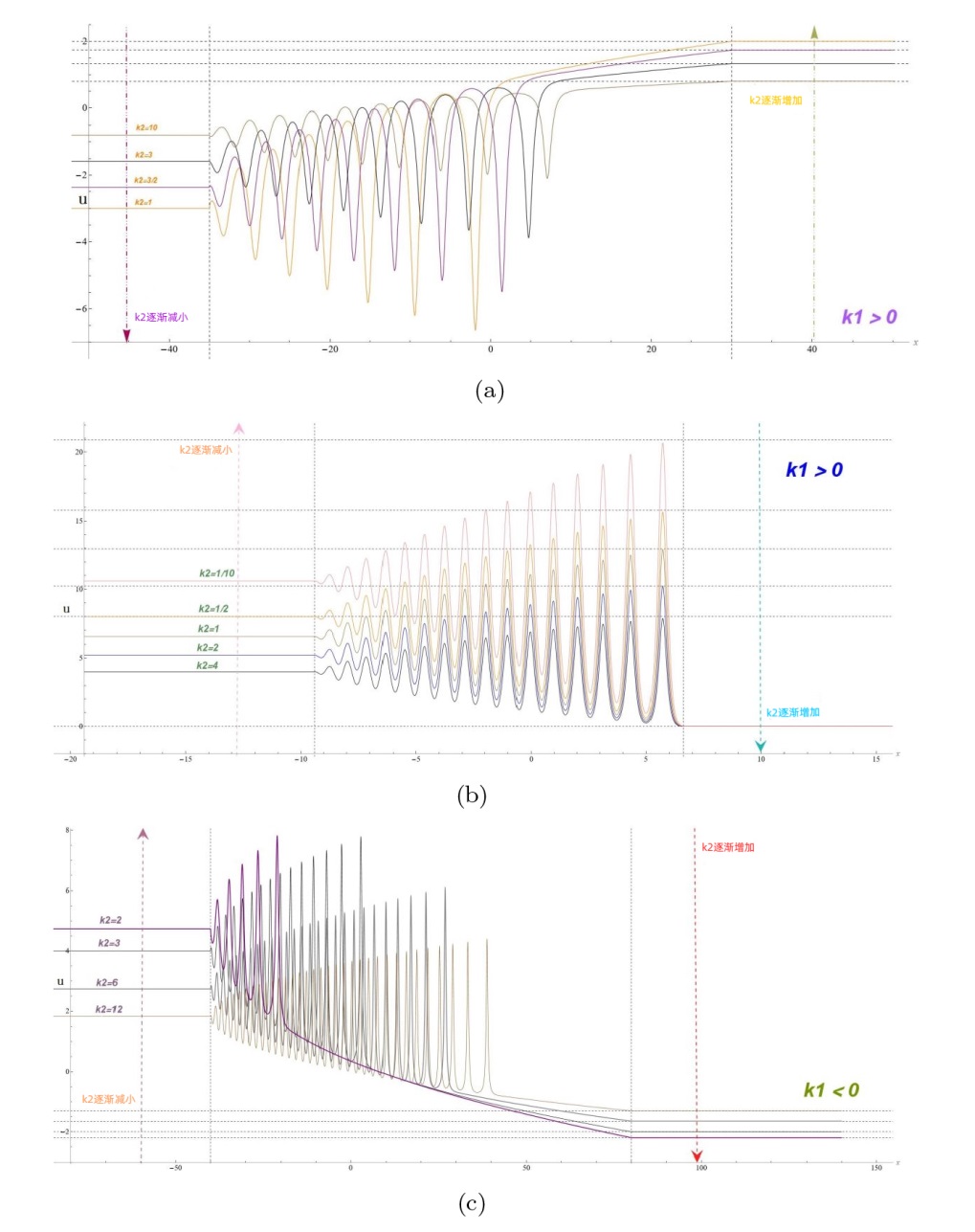
The Complete Classification of Solutions to the Step Initial Condition: Analysis and Numerical Verification for the Generalized Gardner Equation in Fluid Mechanics
Zhang Yan( ),Hao Huiqin*(
),Hao Huiqin*( ),Guo Rui(
),Guo Rui( )
)
- School of Mathematics, Taiyuan University of Technology, Taiyuan 030024
-
Received:2023-10-27Revised:2024-04-29Online:2024-10-26Published:2024-10-16 -
Supported by:NSFC(11905155);Scientific Activities of Selected Returned Overseas Scholars in Shanxi Province(20220008)
CLC Number:
- O322
Cite this article
Zhang Yan, Hao Huiqin, Guo Rui. The Complete Classification of Solutions to the Step Initial Condition: Analysis and Numerical Verification for the Generalized Gardner Equation in Fluid Mechanics[J].Acta mathematica scientia,Series A, 2024, 44(5): 1242-1282.
share this article
| [1] | Infeld E, Rowlands G. Nonlinear Waves, Solitons and Chaos. New York: Cambridge University Press, 1990 |
| [2] | Ablowitz M J, Clarkson P A. Solitons, Nonlinear Evolution Equations and Inverse Scattering. New York: Cambridge University Press, 1991 |
| [3] | Kevrekidis P G, Frantzeskakis D J, Carretero-González R. Emergent Nonlinear Phenomena in Bose-Einstein Condensates. New York: Springer, 2008 |
| [4] | Korteweg D J, De Vries G. On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves. Phil Mag, 1895, 5(39): 422-443 |
| [5] | Miura R M. Korteweg-de Vries equation and generalizations. I. A remarkable explicit nonlinear transformation. J Math Phys, 1968, 9(8): 1202-1204 |
| [6] | Miura R M, Gardner C S, Kruskal M D. Korteweg-de Vries equation and generalizations. II. Existence of conservation laws and constants of motion. J Math Phys, 1968, 9(8): 1204-1209 |
| [7] | Su C H, Gardner C S. Korteweg-de Vries equation and generalizations. III. Derivation of the Korteweg-de Vries equation and Burgers equation. J Math Phys, 1969, 10(3): 536-539 |
| [8] | Gardner C S. Korteweg-de Vries equation and generalizations. IV. The Korteweg-de Vries equation as a Hamiltonian system. J Math Phys, 1971, 12(8): 1548-1551 |
| [9] | Mishra M K, Chhabra R S, Sharma S R. Obliquely propagating ion-acoustic solitons in a multi-component magnetized plasma with negative ions. J Plasma Phys, 1994, 52(3): 409-429 |
| [10] | Horii Z. Formulation of the Korteweg-de Vries and the Burgers equations expressing mass transports from the generalized Kawasaki-Ohta equation. Phys Lett A, 2002, 306: 45-51 |
| [11] |
Apela J R, Ostrovsky L A, Stepanyants Y A, et al. Internal solitons in the ocean and their effect on underwater sound. J Acoust Soc Am, 2007, 121(2): 695-722
pmid: 17348494 |
| [12] | Leblond H, Grelu P, Mihalache D. Models for supercontinuum generation beyond the slowly-varying-envelope approximation. Phys Rev A, 2014, 90: 053816 |
| [13] | Ralph E A, Pratt L. Predicting eddy detachment for an equivalent barotropic thin jet. J Nonlinear Sci, 1994, 4: 355-374 |
| [14] | Das G C, Karmakar B. Nonlinear ion-acoustic waves in multicomponent plasmas. Can J Phys, 1988, 66(1): 79-81 |
| [15] | Chow K W, Grimshaw R H J, Ding E. Interactions of breathers and solitons in the extended Korteweg-de Vries equation. Wave Motion, 2005, 43(2): 158-166 |
| [16] | Bokaeeyan M, Ankiewicz A, Akhmediev N. Bright and dark rogue internal waves: The Gardner equation approach. Phys Rev E, 2019, 99(6): 062224 |
| [17] | Baldwin D, Goktas U, Hereman W, et al. Symbolic computation of exact solutions in hyperbolic and elliptic functions for nonlinear PDEs. J Symb Comput, 2004, 37: 669-705 |
| [18] | Demler E, Maltsev A. Semiclassical solitons in strongly correlated systems of ultracold bosonic atoms in optical lattices. Ann Phys, 2011, 326(7): 1775-1805 |
| [19] | Demiray S T, Bulut H. New exact solutions for generalized Gardner equation. Kuwait J Sci, 2017, 44(1): 1-8 |
| [20] | Grimshaw R. Environmental Stratified Flows. New York: Springer, 2002 |
| [21] | Kakutani T, Yamasaki N. Solitary waves on a two-layer fluid. J Phys Soc Jpn, 1978, 45(2): 674-679 |
| [22] | Hamdi S, Morse B, Halphen B, et al. Analytical solutions of long nonlinear internal waves: Part I. Nat Hazards, 2011, 57(3): 597-607 |
| [23] |
Grimshaw R, Pelinovsky D, Pelinovsky E, et al. Generation of large-amplitude solitons in the extended Korteweg-de Vries equation. Chaos, 2002, 12(4): 1070-1076
pmid: 12779630 |
| [24] | Fan E G. A family of completely integrable multi-Hamiltonian systems explicitly related to some celebrated equations. J Math Phys, 2001, 42(9): 4327-4344 |
| [25] | Meng G Q, Gao Y T, Yu X, et al. Painlevé analysis, Lax pair, Bäcklund transformation and multi-soliton solutions for a generalized variable-coefficient KdV-mKdV equation in fluids and plasmas. Phys Scr, 2012, 85(5): 055010 |
| [26] | Li J, Xu T, Meng X H, et al. Lax pair, Bäcklund transformation and N-soliton-like solution for a variable-coefficient Gardner equation from nonlinear lattice, plasma physics and ocean dynamics with symbolic computation. J Math Anal Appl, 2007, 336(2): 1443-1455 |
| [27] | El G A, Hoefer M A. Dispersive shock waves and modulation theory. Physica D, 2016, 333: 11-65 |
| [28] | Holloway P E, Pelinovsky E, Talipova T. A generalized Korteweg-de Vries model of internal tide transformation in the coastal zone. J Geophys Res Oceans, 1999, 104(C8): 18333-18350 |
| [29] | Scotti A, Pineda J. Observation of very large and steep internal waves of elevation near the Massachusetts coast. Geophys Res Lett, 2004, 31(22): L22307 |
| [30] | Madsen P A, Fuhrman D R, Schäffer H A. On the solitary wave paradigm for tsunamis. J Geophys Res Oceans, 2008, 113(C12): C12012 |
| [31] | Christie D R. The morning glory of the Gulf of Carpentaria: a paradigm for non-linear waves in the lower atmosphere. Austral Met Mag, 1992, 41: 21-60 |
| [32] | Smyth N F, Holloway P E. Hydraulic jump and undular bore formation on a shelf break. J Phys Ocean, 1988, 18(7): 947-962 |
| [33] | Whitham G B. Linear and Nonlinear Waves. New York: Wiley, 1974 |
| [34] | Whitham G B. Non-linear dispersive waves. Math Phys Sci, 1965, 283(1393): 238-261 |
| [35] | An X, Marchant T R, Smyth N F. Dispersive shock waves governed by the Whitham equation and their stability. Proc Math Phys Eng Sci, 2018, 474(2216): 20180278 |
| [36] | El G A, Hoefer M A, Shearer M. Dispersive and diffusive-dispersive shock waves for non-convex conservation laws. SIAM Review, 2017, 59(1): 3-61 |
| [37] | Onorato M, Stefania R, Fabio B. Rogue and Shock Waves in Nonlinear Dispersive Media. New York: Springer, 2016 |
| [38] | Gurevich A V, Pitaevskii L P. Nonstationary structure of a collisionless shock wave. Sov Phys JETP, 1974, 38: 291-297 |
| [39] | Kamchatnov A M. New approach to periodic solutions of integrable equations and nonlinear theory of modulational instability. Phys Rep, 1997, 286(4): 199-270 |
| [40] | Zhang Y, Hao H Q, Guo R. Periodic solutions and Whitham modulation equations for the Lakshmanan-Porsezian-Daniel equation. Phys Lett A, 2022, 450: 128369 |
| [41] | Zhang Y, Hao H Q. Whitham modulation theory and periodic solutions for the fifth-order nonlinear Schrödinger equation in the Heisenberg ferromagnetic spin chain. Nonlinear Dyn, 2023, 111: 12461-12477 |
| [42] | Wang D S, Xu L, Xuan Z. The complete classification of solutions to the Riemann problem of the defocusing complex modified KdV equation. J Nonlinear Sci, 2022, 32(1): 1-46 |
| [43] | Kamchatnov A M. Dispersive shock wave theory for nonintegrable equations. Phys Rev E, 2019, 99(1): 012203 |
| [44] | El G A, Gammal A, Khamis E G, et al. Theory of optical dispersive shock waves in photorefractive media. Phys Rev A, 2007, 76(5): 053813 |
| [45] | Driscoll C F, O' Neil T M. Modulational instability of cnoidal wave solutions of the modified Korteweg-de Vries equation. J Math Phys, 1975, 17(7): 1196-1200 |
| [46] | Kamchatnov A M, Spire A, Konotop V V. On dissipationless shock waves in a discrete nonlinear Schrödinger equation. J Phys A, 2004, 37(21): 5547 |
| [47] | Marchant T R. Undular bores and the initial-boundary value problem for the modified Korteweg-de Vries equation. Wave Motion, 2008, 45(4): 540-555 |
| [48] | Kodama Y, Pierce V U, Tian F R. On the Whitham equations for the defocusing complex modified KdV equation. SIAM J Math Anal, 2009, 40(5): 1750-1782 |
| [49] | Marchant T R, Smyth N F. The extended Korteweg-de Vries equation and the resonant flow of a fluid over topography. J Fluid Mech, 1990, 221: 263-287 |
| [50] | Kamchatnov A M, Kuo Y H, Lin T C, et al. Undular bore theory for the Gardner equation. Phys Rev E, 2012, 86(3): 036605 |
| [51] | Matveev B V. 30 years of finite-gap integration theory. Phil Trans R Soc A, 2008, 366(1867): 837-875 |
| [52] | Kamchatnov A M, Kraenkel R A. On the relationship between a 2×2 matrix and second-order scalar spectral problems for integrable equations. J Phys A: Math Gen, 2002, 35(2): L13-L18 |
| [53] | Ercolani N M, Jin S, Levermore C D, et al. The zero-dispersion limit for the odd flows in the focusing Zakharov-Shabat hierarchy. Int Math Res Notices, 2003, 47: 2529 |
| [54] | Grava T, Klein C. Numerical solution of the small dispersion limit of Korteweg-de Vries and Whitham equations. Commun Pure Appl Math, 2007, 60(11): 1623-1664 |
| [55] | Fornberg B, Whitham G B. A numerical and theoretical study of certain nonlinear wave phenomena. Philos Trans R Soc London Ser A, 1978, 289(1361): 373-404 |
| [1] | Wang Li. The Inverse Problem for the Supersonic Plane Flow Past a Curved Wedge [J]. Acta mathematica scientia,Series A, 2018, 38(4): 679-686. |
|