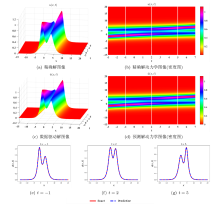
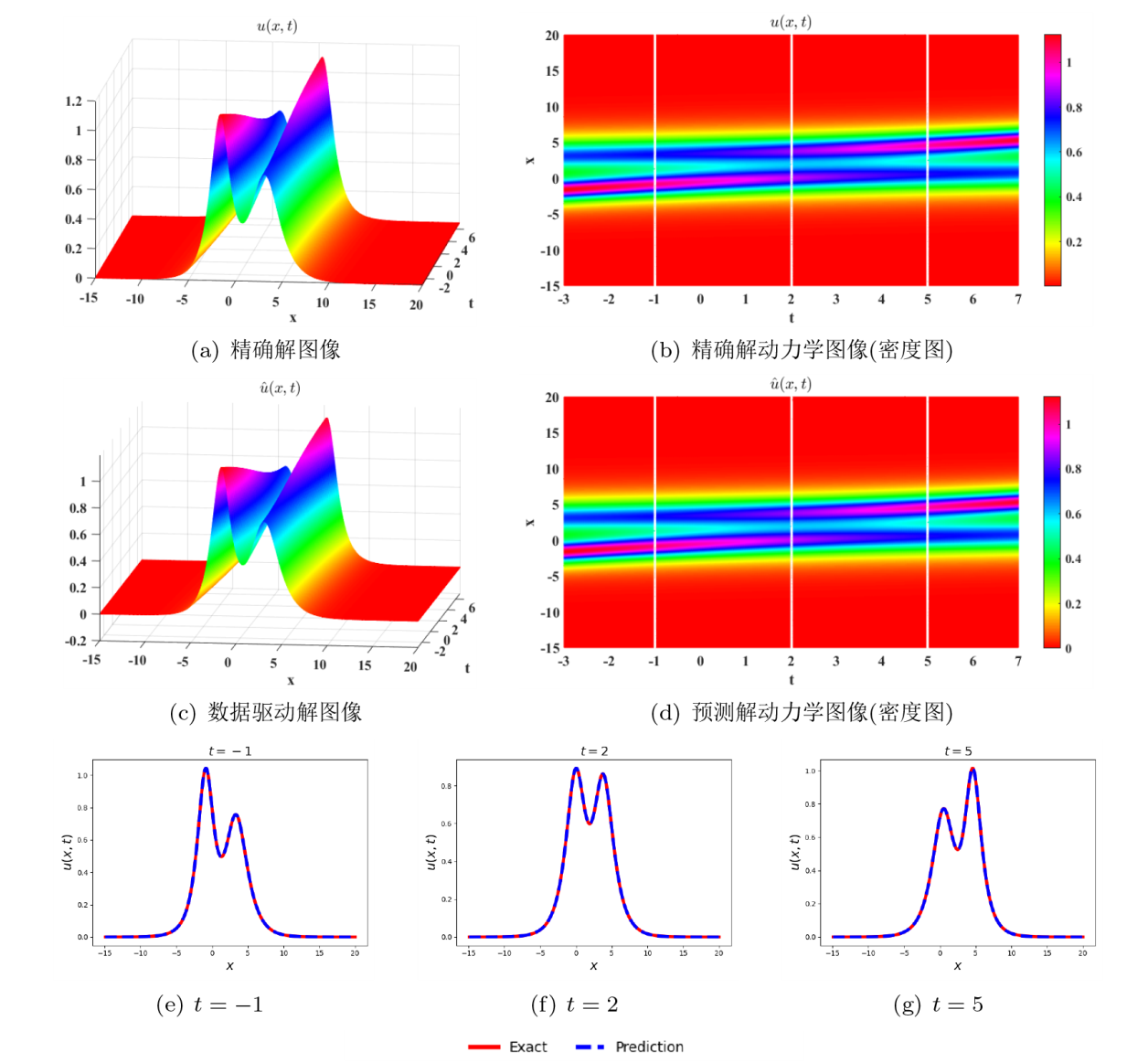
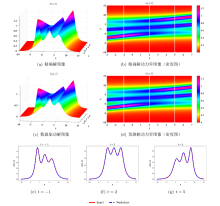
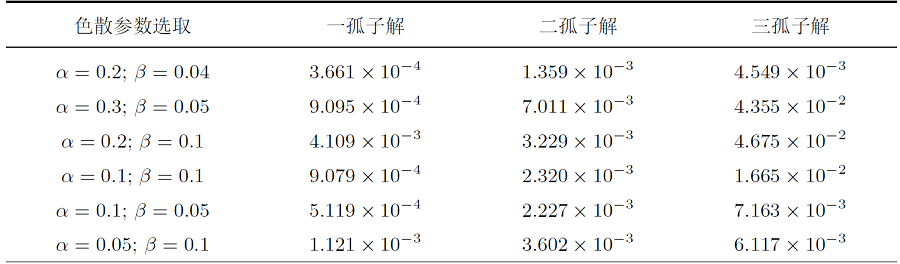
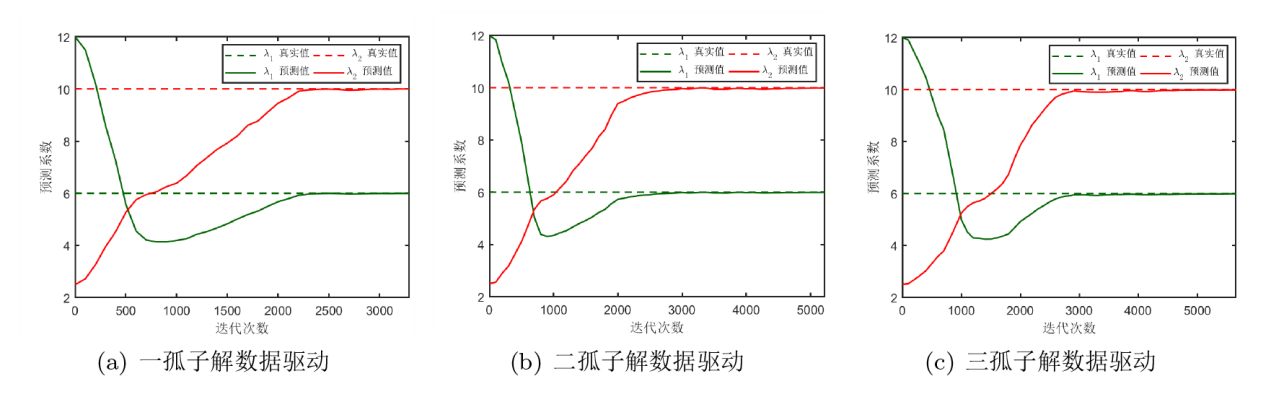
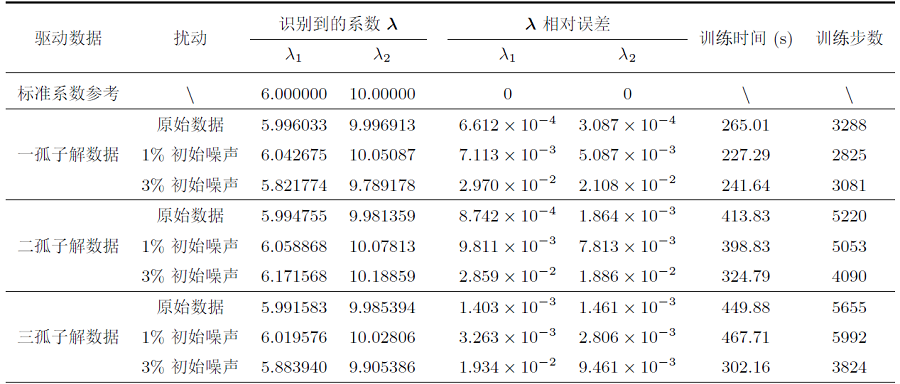
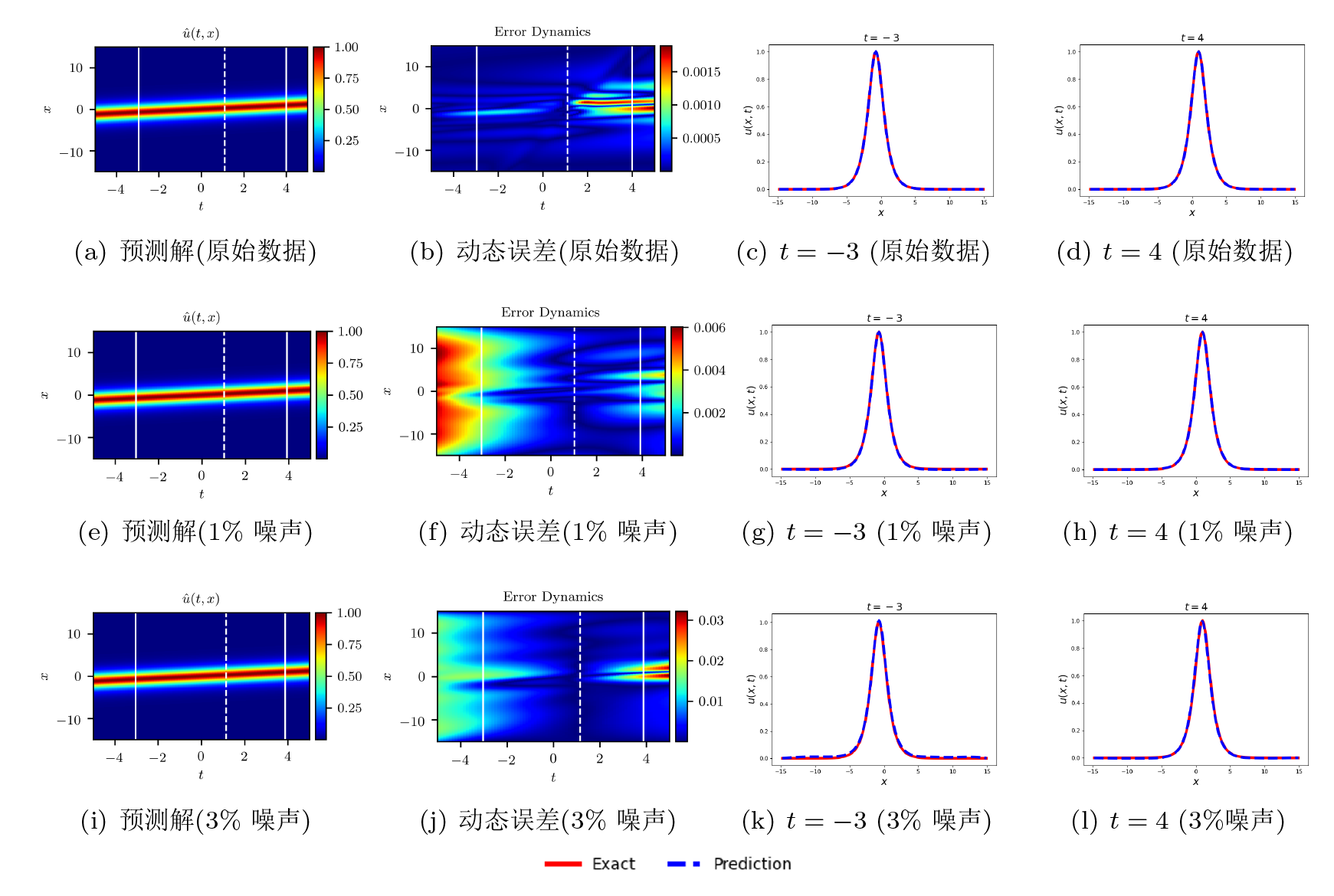
Acta mathematica scientia,Series A ›› 2024, Vol. 44 ›› Issue (2): 484-499.
Previous Articles Next Articles
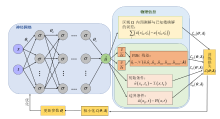
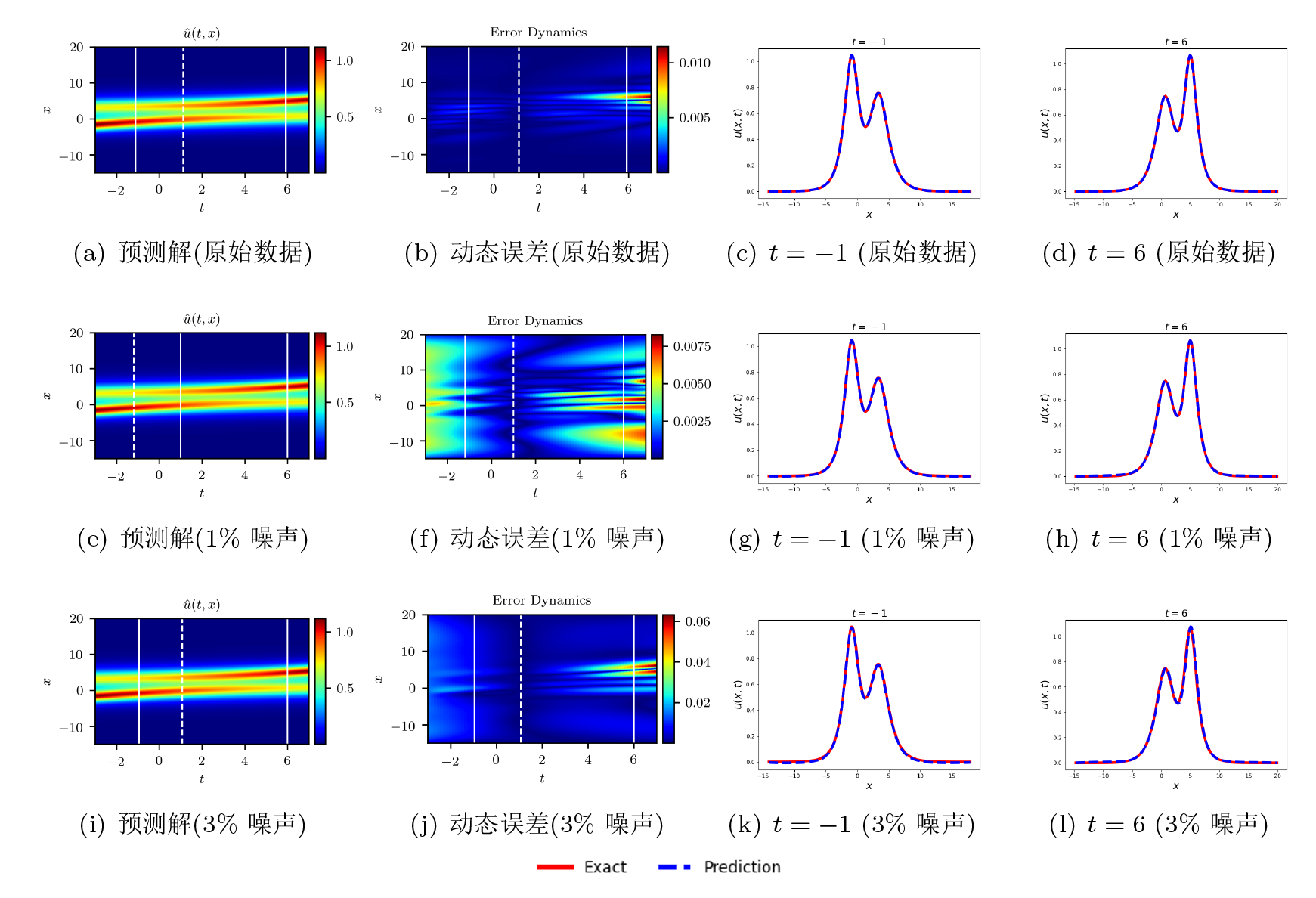
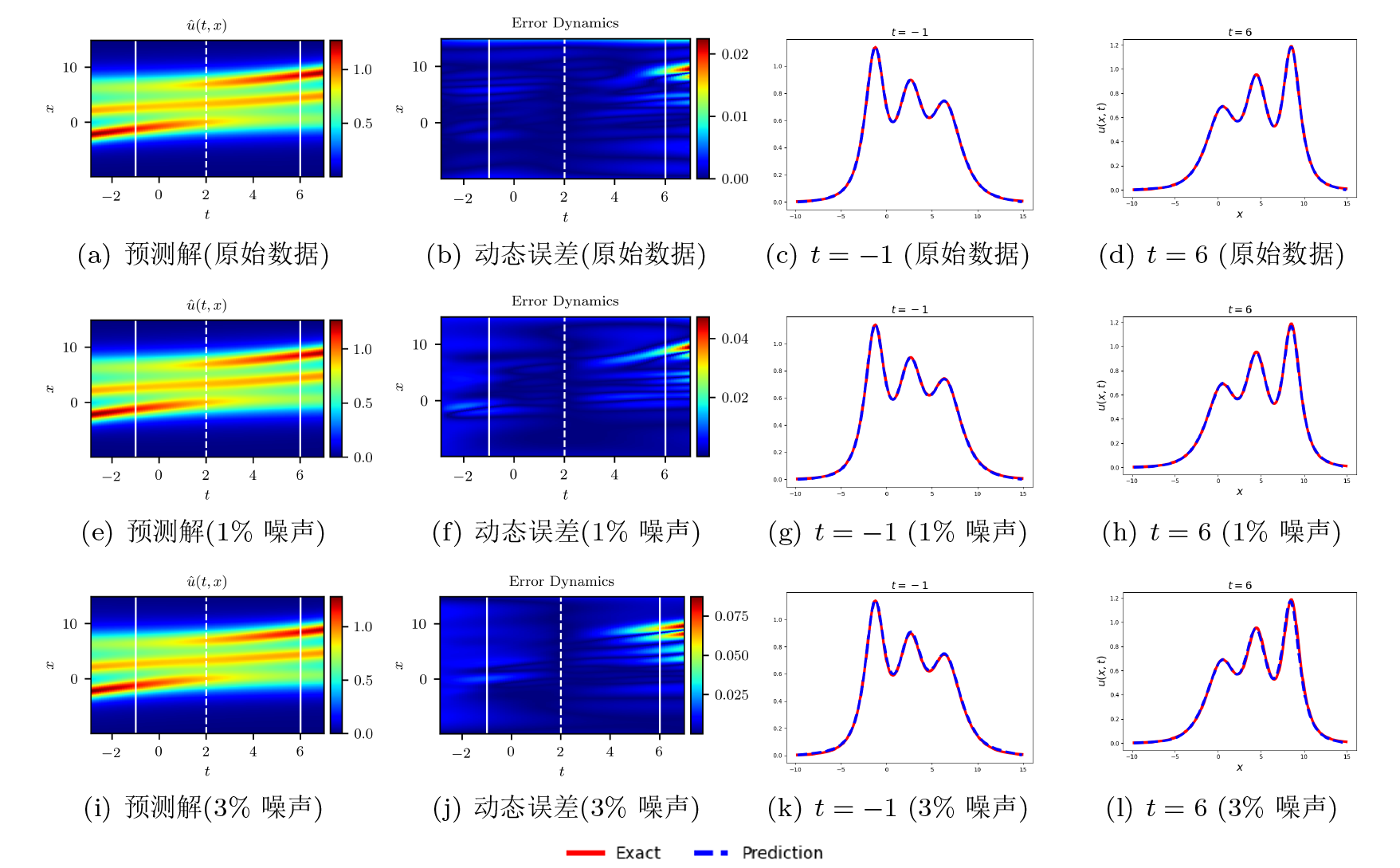
Solving the Forward and Inverse Problems of Extended Fifth-Order mKdV Equation Via Physics-Informed Neural Networks
Wu Zekang,Wang Xiaoli*( ),Han Wenjing,Li Jinhong
),Han Wenjing,Li Jinhong
- School of Mathematics and Statistics, Qilu University of Technology (Shandong Academy of Science), Jinan 250353
-
Received:2023-05-08Revised:2023-10-17Online:2024-04-26Published:2024-04-07 -
Supported by:NSFC(12275017);Natural Science Foundation of Shandong Province(ZR2020MA049)
CLC Number:
- O241.8
Cite this article
Wu Zekang, Wang Xiaoli, Han Wenjing, Li Jinhong. Solving the Forward and Inverse Problems of Extended Fifth-Order mKdV Equation Via Physics-Informed Neural Networks[J].Acta mathematica scientia,Series A, 2024, 44(2): 484-499.
share this article
| [1] | Draper L. Freak wave. Mar Obs, 1965, 35(2): 193-195 |
| [2] |
Haus H A, Wong W S. Solitons in optical communications. Rev Mod Phys, 1996, 68(2): 423-444
doi: 10.1103/RevModPhys.68.423 |
| [3] |
Zabusky N J, Kruskal M D. Interaction of "solitons" in a collisionless plasma and the recurrence of initial states. Phys Rev Lett, 1965, 15(6): 240-243
doi: 10.1103/PhysRevLett.15.240 |
| [4] |
Parkins A S, Walls D F. The physics of trapped dilute-gas Bose-Einstein condensates. Phys Rep, 1998, 303(1): 1-80
doi: 10.1016/S0370-1573(98)00014-3 |
| [5] |
Wadati M. The modified Korteweg-de Vries equation. J Phys Soc Jpn, 1973, 34(5): 1289-1296
doi: 10.1143/JPSJ.34.1289 |
| [6] | 黄念宁. 孤子理论和微扰方法. 上海: 上海科技教育出版社, 1996 |
| Huang N N. Theory of Solitons and Method of Pertubations. Shanghai: Shanghai Scientific and Technological Education Press, 1996 | |
| [7] |
Leblond H, Grelu P, Mihalache D. Models for supercontinuum generation beyond the slowly-varying-envelope approximation. Phys Rev A, 2014, 90(5): 053816
doi: 10.1103/PhysRevA.90.053816 |
| [8] |
Ono H. Soliton fission in anharmonic lattices with reflectionless inhomogeneity. J Phys Soc Jpn, 1992, 61(12): 4336-4343
doi: 10.1143/JPSJ.61.4336 |
| [9] |
Khater A H, El-Kalaawy O H, Callebaut D K. Bäcklund transformations and exact solutions for Alfvén solitons in a relativistic electron-positron plasma. Phys Scr, 1998, 58(6): 545
doi: 10.1088/0031-8949/58/6/001 |
| [10] |
Ito M. An extension of nonlinear evolution equations of the KdV (mKdV) type to higher orders. J Phys Soc Jpn, 1980, 49(2): 771-778
doi: 10.1143/JPSJ.49.771 |
| [11] |
Marchant T R, Smyth N F. Soliton interaction for the extended Korteweg-de Vries equation. IMA J Appl Math, 1996, 56(2): 157-176
doi: 10.1093/imamat/56.2.157 |
| [12] | Marchant T R, Smyth N F. The extended Korteweg-de Vries equation and the resonant flow of a fluid over topography. J Fluid Mech, 1990, 221: 263-287 |
| [13] | Wazwaz A M, Xu G Q. An extended modified KdV equation and its Painlevé integrability. Nonlinear Dyn, 2016, 86: 1455-1460 |
| [14] |
GrimShaw R, PelinovSky E, Poloukhina O. Higher-order Korteweg-de Vries models for internal solitary waves in a stratified shear flow with a free surface. Nonlin Processes Geophys, 2002, 9(3/4): 221-235
doi: 10.5194/npg-9-221-2002 |
| [15] | Pelinovskii E N, Polukhina O E, Lamb K. Nonlinear internal waves in the ocean stratified in density and current. Oceanology, 2000, 40(6): 757-766 |
| [16] | Wang X, Zhang J L, Wang L. Conservation laws, periodic and rational solutions for an extended modified Korteweg-de Vries equation. Nonlinear Dyn, 2018, 92: 1507-1516 |
| [17] |
Liu N, Guo B L, Wang D S, et al. Long-time asymptotic behavior for an extended modified Korteweg-de Vries equation. Commun Math Sci, 2019, 17(7): 1877-1913
doi: 10.4310/CMS.2019.v17.n7.a6 |
| [18] | Baydin A G, Pearlmutter B A, Radul A A, et al. Automatic differentiation in machine learning: a survey. J March Learn Res, 2018, 18: 1-43 |
| [19] | Raissi M, Perdikaris P, Karniadakis G E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys, 2019, 378: 686-707 |
| [20] |
Li J, Chen Y. Solving second-order nonlinear evolution partial differential equations using deep learning. Commun Theor Phys, 2020, 72(10): 105005
doi: 10.1088/1572-9494/aba243 |
| [21] |
Li J, Chen Y. A deep learning method for solving third-order nonlinear evolution equations. Commun Theor Phys, 2020, 72(11): 115003
doi: 10.1088/1572-9494/abb7c8 |
| [22] | Li J H, Chen J C, Li B. Gradient-optimized physics-informed neural networks (GOPINNs): a deep learning method for solving the complex modified KdV equation. Nonlinear Dyn, 2022, 107: 781-792 |
| [23] |
田十方, 李彪. 梯度优化物理信息神经网络 (GOPINNs): 求解复杂非线性问题的深度学习方法. 物理学报, 2023, 72(10): 100202
doi: 10.7498/aps.72.20222381 |
|
Tian S F, Li B. Gradient-optimized physics-informed neural networks (GOPINNs): a deep learning method for solving complex nonlinear problems. Acta Phys Sin, 2023, 72(10): 100202
doi: 10.7498/aps.72.20222381 |
|
| [24] |
Wang L, Yan Z Y. Data-driven rogue waves and parameter discovery in the defocusing nonlinear Schrödinger equation with a potential using the PINN deep learning. Phys Lett A, 2021, 404: 127408
doi: 10.1016/j.physleta.2021.127408 |
| [25] |
Cui S K, Wang Z, Han J Q, et al. A deep learning method for solving high-order nonlinear soliton equations. Commun Theor Phys, 2022, 74(7): 075007
doi: 10.1088/1572-9494/ac7202 |
| [26] |
Li J H, Li B. Mix-training physics-informed neural networks for the rogue waves of nonlinear Schrödinger equation. Chaos, Solitons & Fractals, 2022, 164: 112712
doi: 10.1016/j.chaos.2022.112712 |
| [27] | Jin P Z, Lu L, Tang Y F, et al. Quantifying the generalization error in deep learning in terms of data distribution and neural network smoothness. Neural Networks, 2020, 130: 85-99 |
| [28] | Lu L, Meng X H, Mao Z P, et al. DeepXDE: A deep learning library for solving differential equations. SIAM Rev, 2021, 63: 208-228 |
| [29] |
Wang S F, Yu X L, Perdikaris P. When and why PINNs fail to train: A neural tangent kernel perspective. J Comput Phys, 2022, 449: 110768
doi: 10.1016/j.jcp.2021.110768 |
| [30] | Son H, Jang J W, Han W J, et al. Sobolev training for physics informed neural networks. arXiv proprint arXiv: 2101. 08932.2021 |
| [31] |
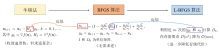
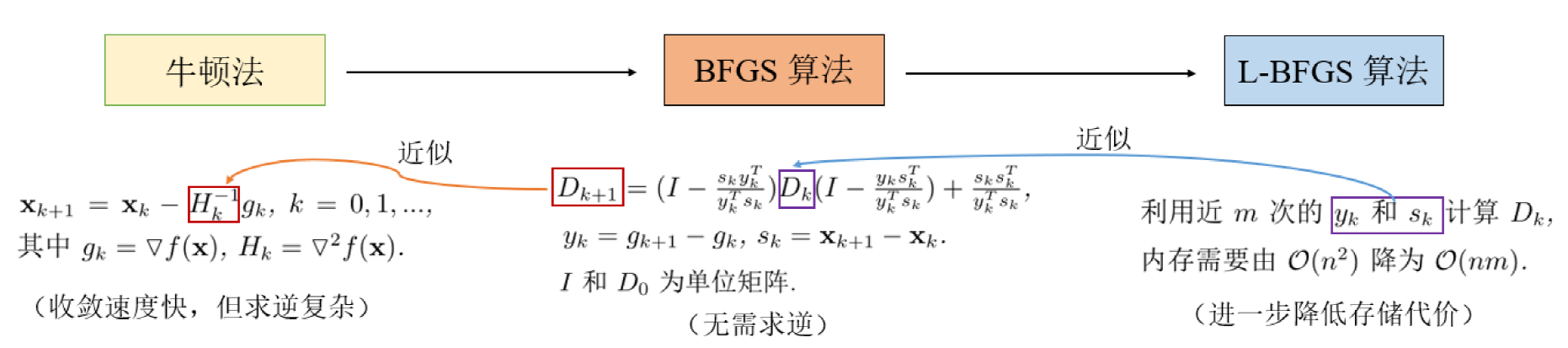
Liu D C, Nocedal J. On the limited memory BFGS method for large scale optimization. Math Program, 1989, 45(1): 503-528
doi: 10.1007/BF01589116 |
| [32] |
Stein M. Large sample properties of simulations using Latin hypercube sampling. Technometrics, 1987, 29(2): 143-151
doi: 10.1080/00401706.1987.10488205 |
| [33] |
Jiao Y L, Lai Y M, Li D W, et al. A rate of convergence of physics informed neural networks for the linear second order elliptic pdes. Commun Comput Phys, 2022, 31(4): 1272-1295
doi: 10.4208/cicp |
| [1] | He Ya, An Jing. An Effective Fourier Spectral Approximation for Fourth-Order Eigenvalue Problems with Periodic Boundary Conditions [J]. Acta mathematica scientia,Series A, 2024, 44(1): 37-49. |
| [2] | Zeng Jiyao,Li Jian. An Adaptive Discontinuous Finite Volume Element Method for the Cahn-Hilliard Equation [J]. Acta mathematica scientia,Series A, 2023, 43(4): 1255-1268. |
| [3] | Wang Yang,Li Jian,Li Yi,Qin Yi. Analysis of a New Time Filter Algorithm for the Unsteady Stokes/Darcy Model [J]. Acta mathematica scientia,Series A, 2023, 43(3): 829-854. |
| [4] | Yu Yikang,Niu Jing. A Kind of Numerical Algorithm for Elliptic Interface Problem [J]. Acta mathematica scientia,Series A, 2023, 43(3): 883-895. |
| [5] | Jian Mangmang, Zheng Supei, Feng Jianhu, Zhai Mengqing. Well-Balanced Preserving of Entropy Stable Schemes for Shallow Water Equations [J]. Acta mathematica scientia,Series A, 2023, 43(2): 491-504. |
| [6] | Yuan Huang,Yue Zhi,Tong Kang,Ran Wang,Hong Zhang. Fully Discrete Finite Element Scheme for a Nonlinear Induction Heating Problem [J]. Acta mathematica scientia,Series A, 2022, 42(4): 1238-1255. |
| [7] | Ying Liu,Jianfang Gao. Oscillation Analysis of a Kind of Systems with Piecewise Continuous Arguments [J]. Acta mathematica scientia,Series A, 2022, 42(3): 826-838. |
| [8] | Yiming Luo,Dingfang Li,Min Liu,Jian Dong. Moving-Water Equilibria Preserving Central Scheme for the Saint-Venant System [J]. Acta mathematica scientia,Series A, 2022, 42(3): 891-903. |
| [9] | Qingchun Meng,Lei Zhang. Numerical Solution of the Three-Dimensional Inverse Heat Conduction Problems [J]. Acta mathematica scientia,Series A, 2022, 42(1): 187-200. |
| [10] | Haiyun Deng,Hui Liu,Wenjing Song. Finite Difference Scheme for the Nonhomogeneous Initial Boundary Value Problem of Critical Schrödinger Map [J]. Acta mathematica scientia,Series A, 2021, 41(5): 1311-1322. |
| [11] | Supei Zheng,Xia Xu,Jianhu Feng,Dou Jia. High Order Sign Preserving Entropy Stable Schemes [J]. Acta mathematica scientia,Series A, 2021, 41(5): 1296-1310. |
| [12] | Keyan Wang,Qisheng Wang. Error Estimates for Expanded Mixed Finite Element Methods for Nonlinear Hyperbolic Equation [J]. Acta mathematica scientia,Series A, 2021, 41(2): 468-478. |
| [13] | Zhihao Ge,Ruihua Li. Numerical Methods for the Critical Temperature and Gap Solution of Bogoliubov-Tolmachev-Shirkov Model [J]. Acta mathematica scientia,Series A, 2020, 40(6): 1699-1711. |
| [14] | Xiaolong Zhao,Meilan Qiu,Xijun Yu,Fang Qing,Shijun Zou. A Second-Order RKDG Method for Lagrangian Compressible Euler Equations on Unstructured Triangular Meshes [J]. Acta mathematica scientia,Series A, 2020, 40(5): 1354-1361. |
| [15] | Zhaolin Yan,Jianfang Gao. Numerical Oscillation Analysis of the Mixed Type Impulsive Differential Equation [J]. Acta mathematica scientia,Series A, 2020, 40(4): 993-1006. |
|